电网不平衡情况下基于神经网络并网逆变器同步技术研究

阳同光

(湖南城市学院 机械与电气工程学院，湖南 益阳 413000)

电网不平衡情况下基于神经网络并网逆变器同步技术研究

阳同光

(湖南城市学院 机械与电气工程学院，湖南 益阳 413000)

为解决常规锁相环技术在电网电压不平衡情况下难以对电网电压频率和相位进行有效检测的问题，提出一种电网不平衡情况下基于神经网络的并网逆变器同步算法。首先，在两相静止坐标系下推导电网电压状态方程，并基于此建立神经网络；然后，利用网络输出电压矢量和实际电压矢量误差进行在线调整权值，并利用权值调整计算在线辨识电网电压频率、相位和幅值，从而可以构建电网电压的正负序分量。仿真和实验结果表明：该方法能在电网不平衡情况下快速有效在线自适应辨识电网电压频率和相位，提取电网电压正负序分量，具有较强的鲁棒性。

电网不平衡；并网逆变器；神经网络；同步;鲁棒性

0 引 言

近年来，随着基于光伏发电、风力发电等绿色再生能源的分布式发电系统的飞速发展，电网及三相并网逆变器的稳定性问题得到了极大的关注[1-4]。并网逆变器需根据电网运行状态实施相应的控制以保证其安全可靠运行。一方面，并网逆变器控制需要检测电网电压同步信号，即基波电压的幅值、相位与频率等信息，确保并网逆变器单位功率因数并网。另一方面，在某些并网逆变器控制算法中需要准确的同步信号参与控制。此外，在电网故障情况下，并网机组必须具备一定的故障穿越能力，需要分布式发电系统能向电网提供无功支持，保证系统可靠运行[5]。传统锁相环在电网电压不平衡情况下无法实现准确锁相，因此，如何在不平衡电网情况下快速准确检测电网电压频率、相位，提取电网电压正负序分量是并网逆变器控制的关键技术之一，已成为可再生能源的研究热点。

同步参考坐标锁相环(synchronous reference frame PLL,SRF-PLL)是应用最为广泛的电网同步方法。SRF-PLL将三相电压通过clarke变换转换到αβ两相静止坐标，然后又通过Park’s坐标变换转变成dq两相旋转坐标系，因此，该方法又称为dq-PLL。在理想电网情况下，SRF-PLL能表现出较为准确的锁相特性，但在不平衡电网情况下，电网电压负序分量中将产生2倍频的波动，不仅对正序分量的幅值提取产生影响，还会对相位检测造成误差[5]。针对这种情况，很多文献提出改进方法，如双同步参考坐标锁相环(doublesynchronousreferenceframe-PLL,DSRF-PLL)[6-7]，解耦双同步参考锁相环(decoupleddoublesynchronousreferenceframe-PLL,DDSRF-PLL)[8-9]，双二阶广义积分器锁相环(doublesecondordergeneralizedintegrator-PLL,DSOGI-PLL)[10-11]，多二阶广义积分器锁相环(multidoublesecondordergeneralizedintegrator-PLL,MSOGI-PLL)[12]，延迟信号消除锁相环(delayedsignalcancellationPLL,DSC-PLL)[13-17]，多复数滤波器锁相环(multiple-complexcoefficientfilterPLL，MCCF-PLL)[18-19]和加强型锁相环(enhancedPLL,EPLL)[20-21]等。虽然这些方法都能在不平衡电网情况下表现出较好的工作性能，但也都存在不足之处：如DDSRF-PLL包含一阶滤波环节，降低了系统的动态响应；DSOGI-PLL由于二阶广义积分器不具备正负序极性选择，导致正负序分量分离环节比较复杂[9]；MCCF-PLL抗干扰能力较差，对电网电压畸变谐波比较敏感；EPLL容易受到电网电压谐波的影响，而延迟信号消除锁相环需要较高的计算成本。此外，基于自适应滤波器(adaptivenotchfilter-PLL,ANF-PLL)[22-23]、自适应矢量滤波(adaptivevectorialfilter-PLL,AVF-PLL)[24]，最小二乘自适应滤波(leasterrorsquaresfilters-PLL,LESF-PLL)[25]等非线性同步技术也被成功应用。这些方法虽然在一定程度上消除了谐波影响，对频率扰动具有一定的抗干扰性，却以降低带宽和动态响应速度为代价[9]。

利用观测器对电网电压频率进行在线识别也是实现锁相的方法之一。文献[26]提出一种基于自适应观测器锁相方法，在静止坐标系下能够准确地观测电网的相位和频率，并且实现正负序分量分离。但其通过引入中间分量构建观测器，观测器设计比较复杂。文献[27]在旋转坐标轴下基于观测器进行正负序分量提取，但其观测器的反馈增益矩阵的极点配置较为复杂。文献[28]采用模型参考自适应观测电网频率，并在基础上进行正负序分量提取，但其关键参数的设计比较复杂。

神经网络具有逼近任意非线性函数的能力，其自学习特性非常适合于周期性和时变扰动情况，如电网电压畸变和参数不确定性，因此，基于神经网络的控制策略能有效提高并网逆变器控制的鲁棒性和自适应性[29]。针对传统锁相环技术在电网不平衡情况下难以有效进行并网同步的问题，提出一种基于神经网络并网逆变器同步方法(neuralnetworkPLL,NN-PLL)。在静止两相坐标系下建立电压状态方程，并基于此构建神经网络，利用网络权值调整在线辨识电网电压频率和相位，并能在基础上进一步实现正负序分量提取，为开展电网不平衡情况下并网逆变器控制提供同步信号。

1 电网不平衡情况下电网模型

为便于分析，不考虑三相电网电压谐波和并网电流谐波，则三相电网电压Ua、Ub、Uc和并网电流Ia、Ib、Ic分别表示为：[UaUbUc]T=

(1)

[IaIbIc]T=

(2)

对式(1)进行Clark变换，可得到αβ两相静止坐标系下电网电压Uα、Uβ表达式

(3)

(4)

(5)

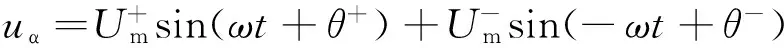
(6)

(7)

同理，对式(2)进行Clark变换，可得到αβ两相静止坐标系下并网电流Iα、Iβ表达式为：

(8)

(9)

(10)

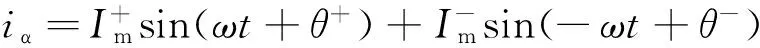
(11)

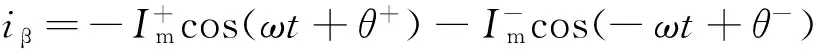
(12)

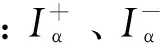
2 基于神经网络自适应同步设计

2.1ADALINE神经网络设计

自适应线性神经元(adaptivelinearneuron,ADALINE)是由美国Standford大学Widrow等[30]提出的。ADALINE是一种多输入、单输出的具有自适应学习特性的单层线性神经元。由于其具有结构简单、易于实现的特点，被广泛用于谐波电流检测[31]和电机参数辨识[32]等。利用ADALINE构建神经网络电网电压频率辨识单元，在电网不平衡情况下在线自适应辨识电网电压正序分量的频率、相位和幅值，并提取电网电压的正负序分量。自适应线性神经网络结构如图1所示，图中，X1、X2、X3为神经网络输入，W1、W2、W3分别为神经网络权值，0为输出。

图1 神经网络单元结构Fig.1 Block diagram of Neural network.

对式(6)和式(7)求导可得：

(13)

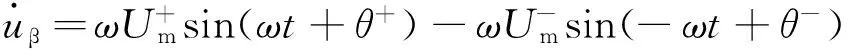
(14)

根据式(6)～式(9)，式(13)和式(14)可写为

(15)

根据三角函数公式

cos(ωt+θ+)=cosωtcosθ+-sinωtsinθ+，

(16)

sin(ωt+θ+)=sinωtcosθ++cosωtsinθ+。

(17)

对式(15)进一步分析可得

(18)

将上式离散化可得

(19)

为便于分析，将上式表示为

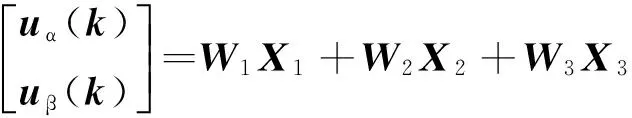
(20)

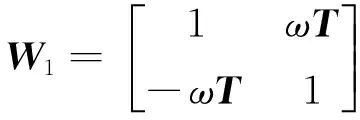
分析上式可知，可以将离散化后的电压状态方程看成具有三个输入节点和一个输出节点的ADA-LINE神经网络结构，其中，X1、X2、X3为神经网络输入，W1、W2和W3分别为三个输入节点的权值。通过在线自适应调整权值W1、W2和W3可求取并网电压正序分量的频率、初相和幅值，从而可得到：

(21)

(22)

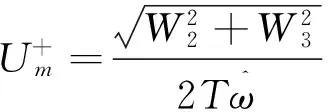
(23)

神经网络权值调整算法采用Wirdow-Hoff学习规则[30]。在采样点k时刻，令误差为

(24)

定义能量函数为

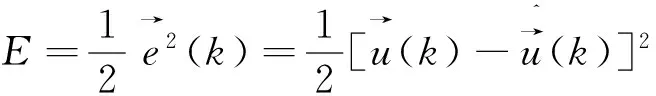
(25)

学习过程神经网络权值变化可表示为

(26)

式中i=1、2、3。则神经网络权值训练表达式为

Wi(k)=Wi(k-1)+ηΔWi(k)。

(27)

其中η为学习率。

基于神经网络的电网电压正序分量的频率、相位和幅值辨识单元结构如图2所示。

2.2 基于ADALINE神经网络正负序分量提取

根据式(21)～式(23)，可以通过神经网络提取静止坐标系下电网电压的正序分量

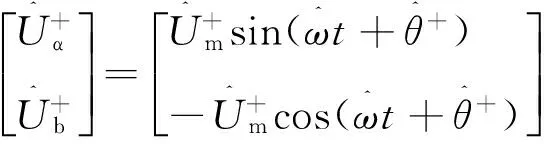
(28)

图2 基于神经网络电网电压频率辨识结构图Fig.2 Diagram of frequency identification based on NN.

根据式(6)、式(7)和式(28)可提取电网电压负序分量为

(29)

根据上述分析，基于神经网络同步算法最终进行电网同步和正负序电压分量提取的整个框图如图3所示。

图3 基于神经网络正负序分量提取结构图Fig.3 Block diagram of positive and negative detect based on NN

3 仿真与实验

为了验证所提出的基于神经网络同步信号检测方法的有效性，在SIMULINK中搭建仿真模型。分别在电网电压单相跌落、含有负序5次谐波和电网频率跳变等3种工况下，对提出的基于ADLINE神经网络同步算法进行仿真，验证NN-PLL方法对电网电压跌落和谐波的抗干扰能力和电网电压的正负序分量分离能力，并网逆变器仿真参数如表1所示，仿真结果分别如图4～图6所示。

表1 仿真参数

图4 单相跌落情况下仿真结果Fig.4 Simulation results when A phase voltage sag

图5 电网电压存在谐波情况下仿真结果Fig.5 Simulation results under harmoic conditions

图5为电网电压存在5次负序谐波情况下的仿真结果图，图5(a)～图5(e)分别为三相电网电压、αβ轴电压分量、负序电压分量、电压相角和频率，从图中看出，当0.4s时刻，电网引入5次负序谐波分量，电源的质量恶化，电网电压波形出现明显畸变情况，但NN-PLL仍然能够有效辨识电网电压频率，进行有效锁相，也能够有效提取电网电压的正负序分量。

图6 电网电压频率突变情况下仿真结果Fig.6 Simulation results when frequency changes

图6为电网电压频率发生突变时仿真结果，在0.4s时刻，电网电压频率有50Hz跳变到55Hz,NN-PLL算法能准确捕捉到频率变化，动态响应较快。

为进一步验证电网同步方法的有效性，采用DSPTMS320F2812数字控制器搭建实验平台进行实验验证。实验参数如表2所示，其中，三相不平衡电压采用一个PWM逆变器经过LC滤波器产生，然后通过AD采样到DSP中解耦。不失一般性，实验所产生的三相电压突变前为有效值220V、频率50Hz的正弦三相电。

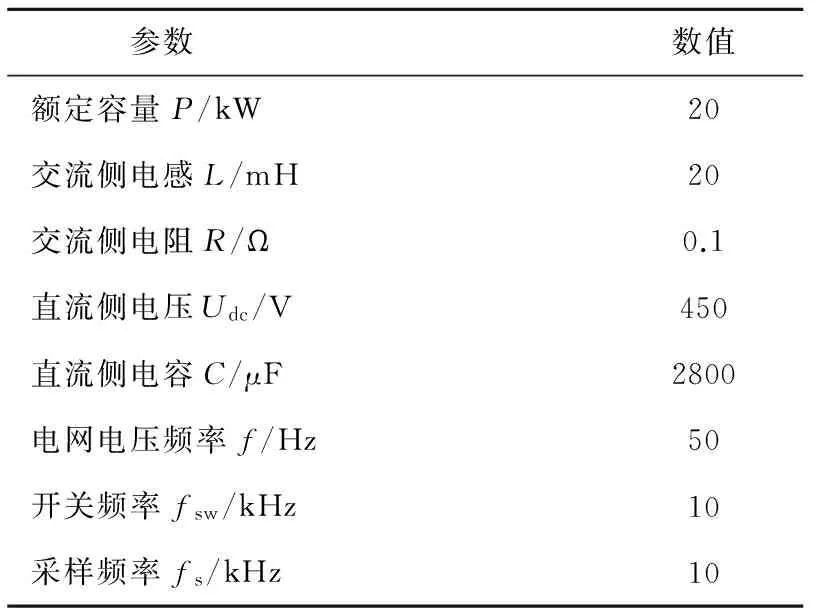
表2 实验参数

图7 单相跌落情况下实验结果Fig.7 Experiment results of NN-PLL under one phase dip fault

为验证NN-PLL算法在电网电压存在谐波情况下的抗干扰能力，用电网模拟装置输出带有10%负序5次谐波的电压。图8为电网存在5次负序谐波情况下实验结果，图中可以看出NN-PLL方法对电网负序谐波进行准确提取，且动态响应较快，虽然电压相角产生一定的畸变，但NN-PLL算法仍然能对其进行准确辨识。

图8 电网谐波情况下实验结果Fig.8 Experiment results of NN-PLL under harmonic condition

图9为电网电压频率产生5 Hz的跳变(50 Hz跳变到55 Hz)的情况下实验结果，从图中可以看出，在频率发生跳变的情况下，NN-PLL方法由于具有在线自适应能力，能有效观测电网电压频率的变化。

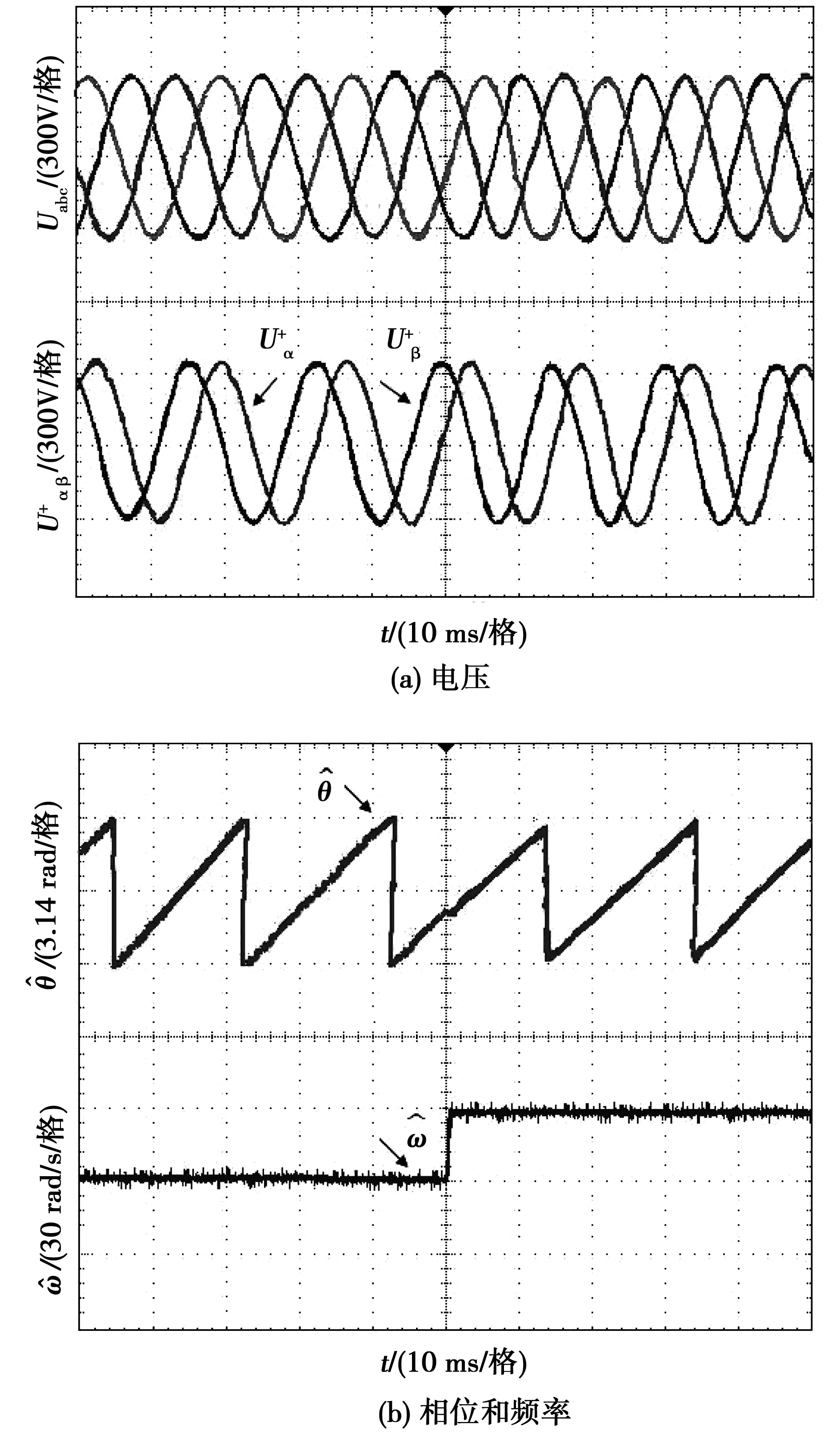
图9 频率跳变情况下实验结果Fig.9 Experiment results of NN-PLL under frequency jump condition

图10 几种PLL动态性能比较Fig.10 Comparison of the dynamic performance for different PLLs

为说明NN-PLL方法的动态性能，将NN-PLL和DSFR-PLL[6]、DSOGI-PLL[10]和DDSFR-PLL[11]方法在电网电压频率发生跳变的情况下进行实验对比，结果如图10所示。从图中可以看出，采用DSOGI- PLL和DSFR-PLL存在较大的超调，而DDSFR-PLL的动态响应速度明显较慢，在动态性能方面，提出的NN-PLL算法具有较强的优越性。

4 结 论

本文针对不平衡电网情况下传统锁相环技术无法有效实现并网逆变器同步的问题，提出一种基于自适应线性神经元神经网络的同步算法。通过仿真和实验验证，可以得出如下结论：

1)该方法能在电网不平衡情况下(单相跌路、谐波和电网频率跳变)有效检测电网电压频率和相位，实现正序、负序分量的准确提取，具有较强的自适应性，且动态响应较快。

2)该方法能同时实现电网电压正负序电压提取、电网电压相角和频率的准确辨识，在此基础上，可非常方便开展电网不平衡情况下并网逆变器控制，可省去常规的电网电压正负序提取环节。

3)和DSFR-PLL、DSOGI-PLL和DDSFR-PLL等方法相比，该方法的抗干扰能力较强，且结构简单，易于实现。

[1] SINSUKTHAVORN W,ORTJOHANN E,MOHD A,et al. Control strategy for three-/four-wire-inverter based distributed generation[J].IEEE Trans. Ind. Electron. 2012. 59(10): 3890-3899.

[2] LEE C T,HSU C W,CHENG P T.A low-voltage ride-through technique for grid-connected converters of distributed energy resources[J].IEEE Trans. Ind. Appl.2011. 47(4):1821-1832.

[3] KESLER M,OZDEMIR E.Synchronous- reference- frame- based control method for UPQC under unbalanced and distorted load conditions[J]. IEEE Trans. Ind. Electron. 2011,58(9): 3967-3975.

[4] KARIMI-GHARTEMANI M,IRAVANI M R.A method for synchronization of power electronic converters in polluted and variable-frequency environments[J]. IEEE Trans. Power Syst.2004. 19(3):1263-1270.

[5] 赵新，金新民，周飞，等. 采用降阶谐振调节器的并网逆变器锁频环技术[J].中国电机工程学报,2013,33(15):38-45. ZHAO Xin,JIN Xinmin,ZHOU Fei,et al. A frequency-locked loop technology of grid-connected inverters based on the reduced order resonant controller[J]. Proceedings of the CSEE,2013,33(15): 38-45.

[6] LENOS H,ELIAS K,FREDE B. A new hybrid PLL for interconnecting renewable energy systems to the grid[J]. IEEE Transactions on industry applications,2013. 49(6):2709-2810.

[7] DASILVA C H,PEREIRA R R,DA SILVA L E B,et al.A digital PLL scheme for three-phase system using modified synchronous reference frame[J].IEEE Trans. Ind. Electron. 2010,57(11):3814-3821.

[8] RODRIGUEZ P,POU J,BERGAS J,et al. Decoupled double synchronous reference frame PLL for power converters control[J]. IEEE Trans. Power. Electron.2007. 22(2): 584-592.

[9] 李珊瑚,杜雄,王莉萍,等.解耦多同步参考坐标系电网电压同步信号检测方法[J].电工技术学报,2011,26(12):183-189. LI Shanhu,DU Xiong,WANG Liping,et al. A grid voltage synchronization method based on decoupled multiple synchronous reference frame[J]. Transactions of china electrotechnical society. 2011,26(12):183-189.

[10] 薛尚青,蔡金锭. 基于二阶广义积分器的基波正负序分量检测方法[J].电力自动化设备,2011,31 (11): 69-74. XUE Shangqing，CAI Jinding. Detection of fundamental positive and negative sequence components based on second-order generalized integrator[J]. Electric Power Automation Equipment,2011,31(11):69-74.

[11] 邓哲,周峰武,林辉品.电网故障时基于双输入SOGI-FLL的新型电网快速同步方法[J].电工技术学报,2013,28(12):32-41. DENG Zhe,ZHOU Fengwu,LIN Huipin. A novel fast grid-synchronization method under grid failure based on dual-input SOGI-FLL[J]. Transactions of china electrotechnical society,2013,28(12):32-41.

[12] PEDRO R,ALVARO L,IGNACIO C.Multiresonant frequency-locked loop for grid synchronization of power converters under distorted grid conditions[J]. IEEE Trans. Ind. Electron.,2011,58(1):127-138.

[13] WANG Yifei,LI Yunwei. Analysis and digital implementation of cascaded delayed-signal- cancellation PLL[J]. IEEE Transactions on power electronics,2011. 26(4):1067-1081.

[14] NEVES F A S,CAVALCANTI M C,DE SOUZA H E P,et al. A generalized delayed signal cancellation method for detecting fundamental-frequency positive-sequence three phase signals[J].IEEE Trans. Power Del. 2010,25(3):1816-1825.

[15] NEVES.F A S,DE SOUZA H E P,CAVALCANTI M C,et al. Digital filters for fast harmonic sequence components separation of unbalanced and distorted three-phase signals[J].IEEE Trans. Ind. Electron.2012. 59(10): 3847-3859.

[16] WANG Y,LI Y. Three-phase cascaded delayed signal cancellation PLL for fast selective harmonic detection[J]. IEEE Trans. Ind. Electron.2013,60(4): 1452-1463.

[17] 吴恒,杨东升,阮新波.基于串联信号延迟对消法的三相非理想电网锁相控制策略[J]. 电工技术学报,2014,29(8): 255-264. WU Heng,YANG Dongsheng,RUAN Xinbo. Phase-locked loop based on cascaded delayed signal cancellation for distorted grid[J]. Transactions of China Electrotechnical Society,2014,29(8): 255-264.

[18] GUO Xiaoqiang，WU Weiyang，CHEN Zhe．Multiple complex coefficient-filter-based phase-locked loop and synchronization technique for three-phase grid-interfaced converters in distributed utility networks[J]．IEEE Trans. Ind. Electron.，2011,58(4): 1194-1204．

[19] CRISTIAN B,DAVID R,FERNANDO B,et al. Grid synchronization of three-phase converters using cascaded complex vector filter PLL[C]//Energy Conversion Congress and Exposition (ECCE),2012 IEEE.196-203.

[20] GHARTEMANI M，IRAVANI M．A method for synchronization of power electronic converters in polluted and variable-frequency environments [J]．IEEE Trans. On Power Systems，2004，19(3): 1263-1270．

[21] MASOUD K G,OOI B T. Application of enhanced phase-locked loop system to the computation of synchrophasors[J]. IEEE Trans. Power Del.,2011,26(1):22-32.

[22] PEDRO R,ALVARO L,RA′UL S M A.A stationary reference frame grid synchronization system for three-phase grid-connected power converters under adverse grid conditions[J]. IEEE Trans. Power. Electron.,2012. 27(1):99-112.

[23] 杜雄，郭宏达，孙鹏菊.基于ANF-PLL的电网电压基波正负序分离方法[J]. 中国电机工程学报,2013,33 (27):28-36. DU Xiong,GUO Hongda,SUN Pengju. A positive and negative sequence component separation method for grid voltage based on the phase locked loop with an adaptivenotch filter[J]. Proceedings of the CSEE,2013,33 (27):28-36.

[24] SERGIO V,JUAN A S,MANUEL R R,et al.Adaptive vectorial filter for grid synchronization of power converters under unbalanced and/or distorted grid conditions[J]. IEEE Trans. Ind. Electron.,2014. 61(3):1355-1368.

[25] CHEN Guodong,ZHANG Liang. A novel SPLL and voltage sag detection based on les filters and improved instantaneous symmetrical components method[J]. IEEE Trans. Power Electron.,2015,30(3): 1177-1189.

[26] 霍现旭，胡书举，许洪华. 电网不平衡下基于自适应观测器的锁相环研究[J].电力系统保护与控制,2013,41(15):120-126. HUO Xianxu,HU Shuju,XU Honghua. Phase-locked loop algorithm based on adaptive observer under unbalanced grid voltage condition[J]. Power System Protection and Control,2013,41(15): 120 -126.

[27] PARK Y,SUL S K,KIM W C.Phase-Locked Loop Based on an Observer for Grid Synchronization[J].IEEE Trans. Ind. Appl.,2014,50(2):1256-1265.

[28] 裴喜平,郝晓弘,陈伟.基于模型参考自适应算法的三相锁相环系统[J].电工技术学报,2014,29(4): 196-205. PEI Xiping,HAO Xiaohong,CHEN Wei. A novel three-phase phase-locked-loop system based on model reference adaptive algorithm[J]. Transactions of China Electrotechnical Society,2014,29(4): 196-205.

[29] YASSER A R I M,EHAB F E.A robust natural-frame-based interfacing scheme for grid-connected distributed generation inverters[J]. IEEE Trans. Energy Con.,2011. 26,(3): 728-736.

[30] WIDROW B,LEHR M A. 30 years of adaptive neural networks: Perceptrons,madaline and back propagation [J]. IEEE Proc,1990,78(9):1415-1442.

[31] ABDESLAM D O.A unified artificial neural network architecture for active power filters[J].IEEE Trans. Ind. Electron. 2007.54(l):61-76.

[32] BECHOUCHE A.A novel method for identifying parameters of induction motors at standstill using ADALINE[J]. IEEE Trans. Energy Con.,27(1):105-116.

(编辑：贾志超)

Research on grid synchronization of grid-connected inverter based on neural network under unbalanced voltage conditions

YANG Tong-guang

(College of Mechanic and Electrical Engineering，Hunan City University,Yiyang 413000,China)

To solve the problem of conventional phase locked loop technique under the condition of unbalanced power grid voltage,a grid inverter synchronous technology based on neural network under unbalanced power grid case is developed. At first,grid voltage state equation was derived in the two-phase stationary coordinates,and a neural network was built based on the state equation; the biases of output voltage vector and the actual voltage vector were used to adjust the neural network weight online,and thus to find out the amplitude,frequency and the phase of the grid voltage,which can construct the positive and negative components of grid voltage. Simulation and experimental results show that the method can be online adaptive to identify the frequency and the phase of grid voltage quickly and efficiently in the case of unbalanced power grid,detect the positive and negative sequences of grid voltage,and has strong robustness.

grid voltage unbalance;grid-connected inverter;neural network;synchronization;robust

2016-04-20

国家自然科学基金重点资助项目(51037004);湖南省自然科学基金(2017JJ2022);湖南省教育厅科学研究重点项目(17A036)

阳同光(1974—)，男，博士，副教授，研究方向为智能控制、故障诊断。

阳同光

10.15938/j.emc.2017.06.009

TM 315

A

1007-449X(2017)06-0066-09