带电阻在线辨识的改进型永磁同步电机滑模观测方法

张勇军， 汪伟， 张小庆， 肖雄， 尚敬

(1.北京科技大学 工程技术研究院，北京 100083； 2.中车株洲电力机车研究所有限公司，湖南 株洲 412001)

带电阻在线辨识的改进型永磁同步电机滑模观测方法

张勇军1， 汪伟1， 张小庆1， 肖雄1， 尚敬2

(1.北京科技大学 工程技术研究院，北京 100083； 2.中车株洲电力机车研究所有限公司，湖南 株洲 412001)

针对永磁同步电机定子电阻的不确定性及传统滑模观测存在的固有抖振问题，提出一种带电阻在线辨识的无速度传感器改进型滑模观测方法。该方法在传统滑模观测器的基础上，采用可变边界层厚度的Sigmoid函数来取代Sign函数，并结合转速大小动态调整观测器增益；同时引入电阻在线辨识环节，运用李雅普诺夫函数设计了电阻参数在线辨识算法，并用于实时修正滑模观测器参数。仿真和实验结果表明，与传统的滑模观测器相比，该算法能够有效地抑制滑模观测器的抖振现象，转速估计对电阻变化的鲁棒性得到增强，提高了永磁同步电机驱动系统在整个调速范围内的观测精度。

永磁同步电机；滑模观测器；Sigmoid函数；电阻在线辨识

0 引 言

永磁同步电机(permanent magnet synchronous motor，PMSM)体积小、重量轻、结构简单，具有效率高、转矩电流比高、功率密度高、转动惯量低等优点，在工业驱动领域已经获得广泛应用[1]。在针对PMSM的矢量控制系统中，要满足系统高性能控制要求，需获取准确可靠的转子位置及速度信号。电机的位置和速度信号一般是通过电机的转轴上机械式传感器获得的，然而使用机械式传感器会提高系统维护的难度，且其精度易受环境条件的影响。因此，运用无传感器控制技术在线估计电机转速及转子位置对永磁同步电机的控制有着重要的意义，也是目前研究的热点问题之一。

目前应用于永磁同步电机转速辨识及转子位置估算的方法主要有以下几种：基于PMSM基本电磁关系估计法[2-3]；模型参考自适应方法[4]；高频信号注入法[5]；扩展卡尔曼滤波法[6]；滑模观测器法[7]。其中滑模观测器法具有算法结构相对简单、动态响应快、易于工程实现等优点，广泛应用于永磁同步电机无传感器控制系统。

传统滑模观测器采用Sign函数作为切换函数，容易产生高频抖振，一般需要对观测过程采用滤波等算法对抖振问题加以抑制。文献[8]采用分段线性补偿对位置估算误差进行补偿，提出两级滤波的滑模观测器以实现对PMSM转子位置和速度估算，并对电流、反电势、位置和速度的估算及负载扰动和动态过程进行了分析，通过实验证明了其可行性；文献[9]采用反电势反馈增益系数的自适应算法调节来实现不同速度运行时转子角度估算的误差补偿，有效改善了低速时的抖振和观测算法精度，但对于高速时的滑模抖振抑制作用并不明显。在此基础之上，文献[10]提出了一种基于饱和函数趋近律的改进型滑模观测器算法，有效降低了滑模观测器中普遍存在的抖振现象，但是完全消除估算信号的高频脉振仍需依赖滤波器的合理设计。上述方法中大多都是通过引入滤波器的方式对高频信号进行滤波，会带来转角相位偏差，需要进行相位补偿，一定程度上增加了系统的复杂性。

除滑模抖振外，电机运行过程中的参数会随工况环境发生波动，如温升、集肤效应等原因引起的电阻值变化，由于滑模观测器中需要获取准确的定子电阻等参数，若计算采用的电阻值与实际值出现偏差，会使转速估计出现较大误差且有可能导致系统不稳定[11]。用于交流电机电阻在线辨识的方法有多种，且不少能取得满意的效果[12-14]，但还缺乏有效的针对无传感器PMSM滑模观测的电阻在线估计算法。

本文在传统滑模观测器的基础上，提出了一种改进型滑模观测方法进行转速估计及转子位置预测。首先，以可变边界层厚度的Sigmoid函数取代Sign函数，用来改善由于Sign函数的开关特性而引起的系统抖振，由于去除了传统滑模观测器中的滤波和相位补偿环节，简化了系统，也提高了反电动势的估算精度。同时，考虑到定子电阻的变化对电机速度的辨识精度有影响，在该滑模观测器中加入电阻在线辨识环节，运用李雅普诺夫函数，在滑模观测器的稳定性判据中引入定子电阻误差项，设计了一种电阻参数在线辨识的算法，实时调整滑模观测器辨识模型，有效消除了电阻参数变化对速度辨识精度的影响。在完成基于电阻在线辨识的改进滑模观测器结构设计的基础上，分别采用仿真和实验的方法对无传感器PMSM控制系统的观测精度和静动态响应性能进行了对比测试。

1 无传感器PMSM的滑模观测方法

PMSM是一个非线性的时变系统，为简化分析，在忽略电机铁心的饱和及涡流、磁滞损耗等因素的前提下，其在αβ静止坐标下的数学模型[15]可以表示为

(1)

式中：iα、iβ为α轴和β轴定子电流分量；vα、vβ为α轴和β轴定子电压分量；R、L为定子电阻、电感；eα、eβ为α轴和β轴的反电动势。

而反电动势可表示为

(2)

式中:ψf为永磁体磁链；ω电机转子角速度；θ为转子角位置。

若构造定子电流滑模观测器

(3)

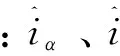
(4)

式中:Ksw为滑模增益系数；sign(x)为开关函数。

定义该滑模观测器的滑模面为

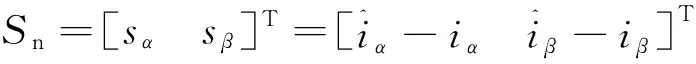
(5)

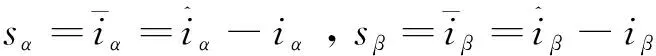
到达滑模面时有Sn=0，即

(6)

则当增益Ksw满足系统的可达性条件时，系统将在有限时间内进入滑动模态。系统稳定后，状态变量会在滑模面进行高速的滑模切换，根据等效控制理论，可得

(7)

由式(4)可知，uαβ(t)由电流误差的高频开关切换得到，不仅包含反电动势的信息，还含有高频干扰信号。为此，采用一阶低通滤波器对高频信号进行滤波，但这会带来转角相位偏差，所以需要进行相位补偿。传统滑模观测器结构如图1所示。

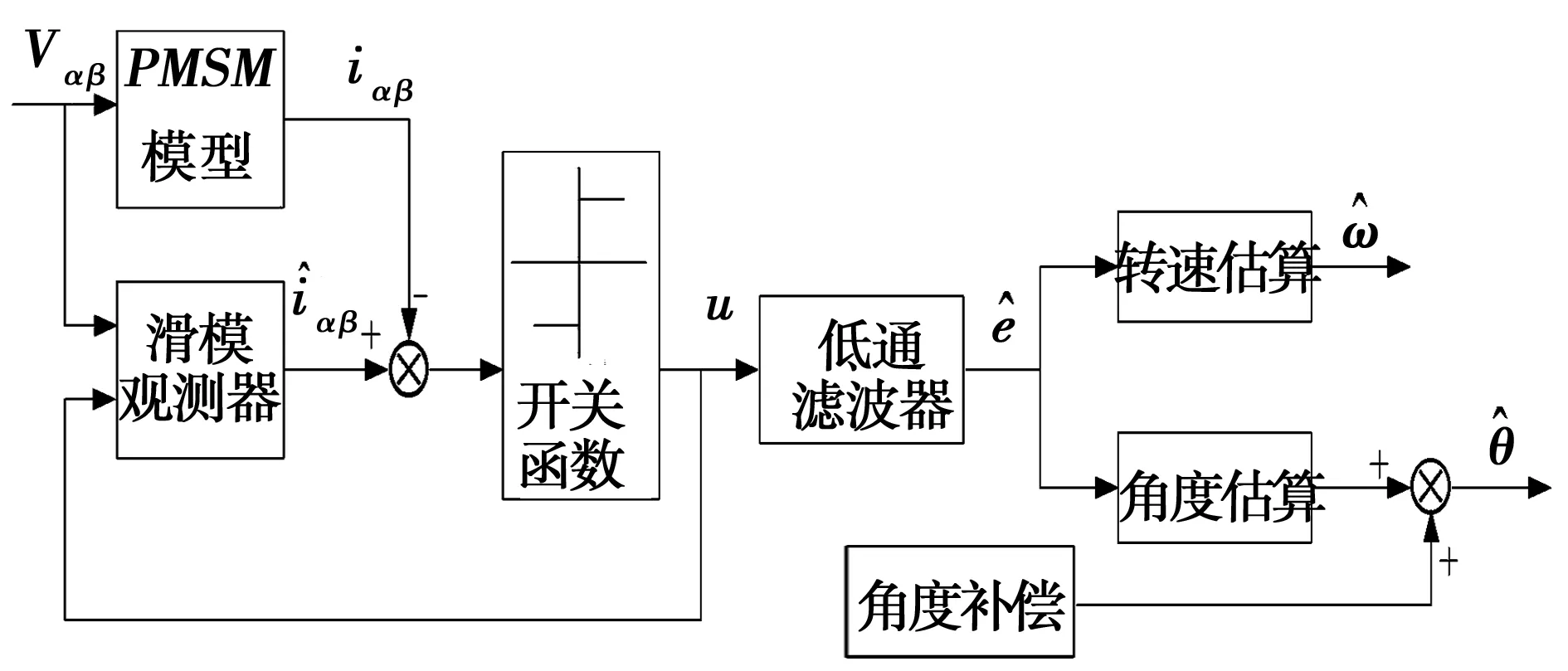
图1 传统滑模观测器结构图Fig.1 Structure diagram of conventional sliding mode observer

2 电阻在线辨识的改进型滑模观测方法

上述滑模观测器采用的是Sign函数作为切换函数，由于Sign函数的开关特性，当状态变量进行高速滑模切换时会引起系统的抖振。抖振的存在提高了滑模变结构控制的抗扰动能力，但同时也会引起系统波动，这种情况在估算量变化较大的高速区域表现得更为明显。为减少被估量产生的谐波，可适当减小观测器的增益值，但这可能会导致系统不稳定，应有对应的自适应和稳定控制方法。

在改进的滑模观测方法中，通过采用可变边界层厚度的Sigmoid函数代替Sign函数，不仅去除了低通滤波器及其相位补偿环节，还可以使观测器增益随速度大小动态调整，同时考虑在滑模观测器的稳定性判据中，引入定子电阻误差项，设计了一种电阻参数在线辨识的算法，实时调整滑模观测器辨识模型，用以解决因电阻参数变化影响速度辨识精度的问题。

2.1 基于Sigmoid函数的滑模观测器

在设计滑动模态控制系统时，用饱和函数代替切换函数实现准滑动模态控制，即在边界层以外采用正常的滑模控制，在边界层内为连续状态的反馈控制，这样可有效地避免或削弱抖振[16-17]。

基于这一理论，利用严格单调的Sigmoid函数代替Sign函数来设计滑模观测器。构造PMSM定子电流滑模观测器为

(8)

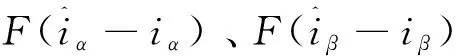
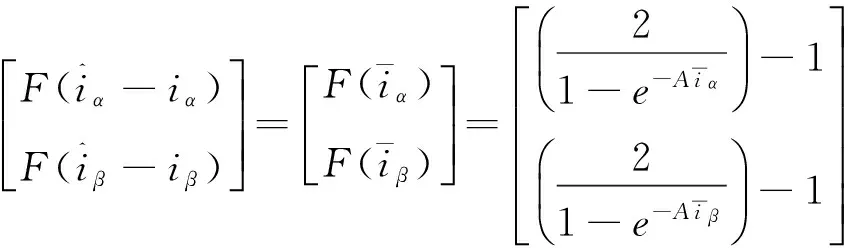
(9)

式中A为Sigmoid函数的斜率系数。

以Sigmoid函数代替Sign函数的方法后，可以采用随转速变化改变Sigmoid函数边界层厚度的方法来进一步抑制滑模抖振。当PMSM高速运行时，定子电压与低速时相比要大得多，这就需SVPWM调制下的逆变器输出更大的电压，也就意味着空间电压矢量作用的时间要加长。为了保证PMSM高速时开关的响应时间，需要降低系统的响应速度，使滑模观测器的边界层厚度变宽。若保持边界层厚度不变，PMSM高速运行时系统会发生剧烈抖振，而低速时系统响应速度变慢，鲁棒性减弱。图2显示了随电机转速变化而改变Sigmoid函数边界层厚度的方法。

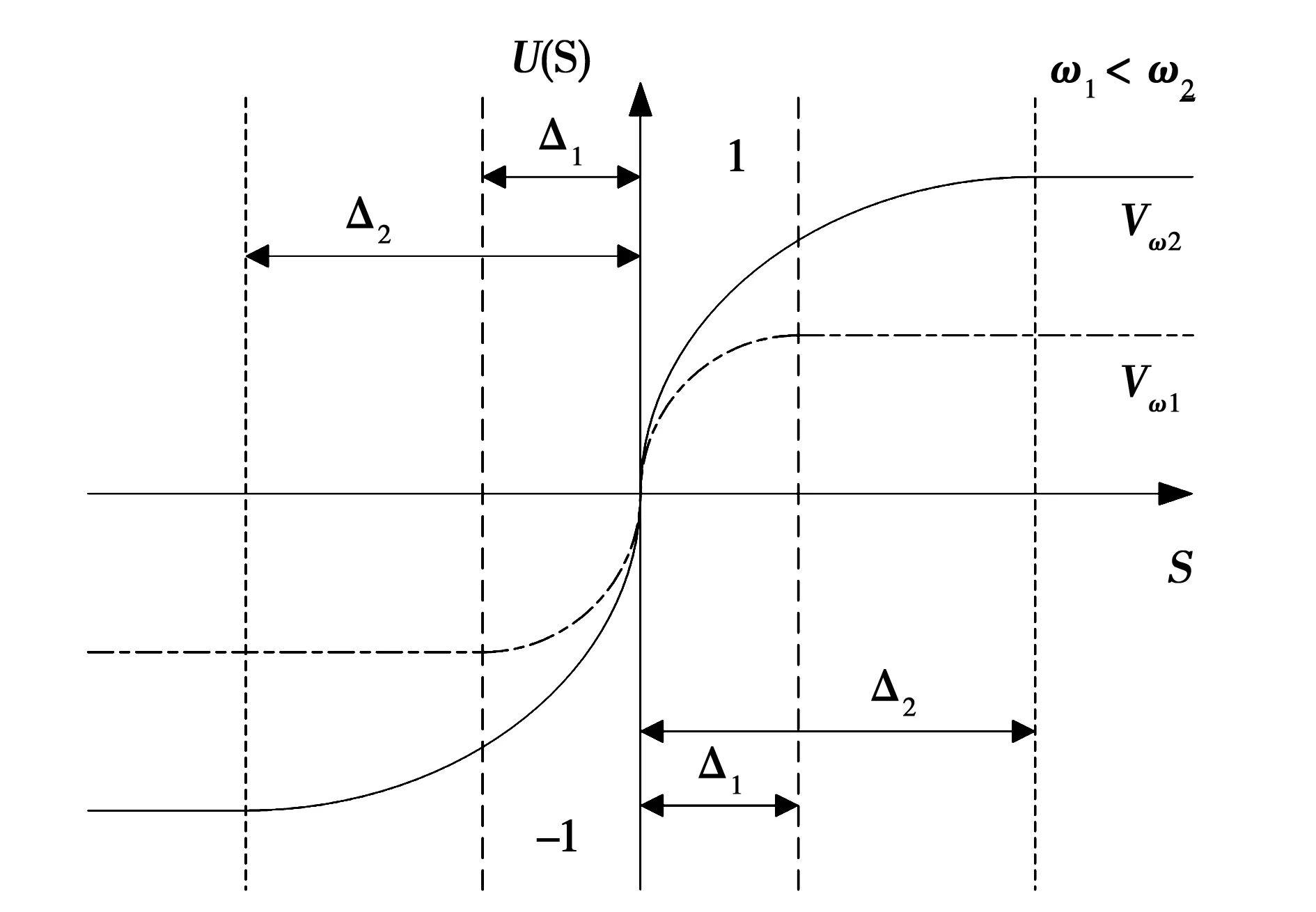
图2 边界层厚度可变Sigmoid函数Fig.2 Sigmoid function with a variable boundary layer

为解决不同速度范围中的抖振问题，将观测器增益k设计为根据转速变化的自适应开关增益，这样就可使Sigmoid函数边界层厚度随转速变化而变化。观测器增益k的表达式如下

k=k0ω。

(10)

式中，k0为一个大于1的常数。

(11)

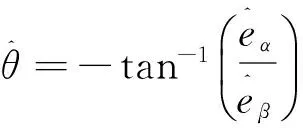
(12)

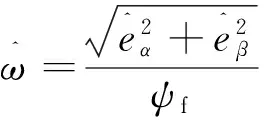
(13)

采用Sigmoid函数后可以取消用于高频干扰的低通滤波器和相应的相位补偿环节，观测器结构也得到简化。图3所示为基于Sigmoid函数的滑模观测器结构。

2.2 定子电阻在线辨识与系统稳定性证明

上文采用可变边界层厚度的Sigmoid函数代替Sign函数可实现根据速度区间变化来进行滑模观测，但注意到观测器中存在定子电阻项，电阻参数受电机内部温度影响变化较大，尤其当PMSM高速运行时，这种影响使得PMSM数学模型准确度发生波动，从而降低系统辨识的精度。在滑模观测器中合理引入定子电阻的在线辨识环节，实时调整滑模观测器辨识模型，有利于提高系统整体的观测和控制精度。

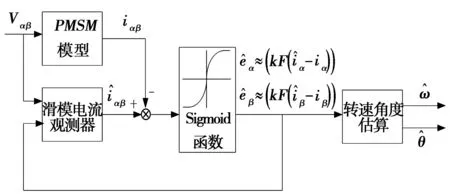
图3 基于Sigmoid函数的滑模观测器结构图Fig.3 Structure diagram of sliding mode observer based on Sigmoid function

根据式(8)的滑模观测器状态方程，将定子电阻在线辨识的电流滑模观测器设计为

(14)

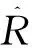
由式(14)与式(1)相减得到的估算电流误差的微分方程为

(15)

构造李雅普诺夫函数

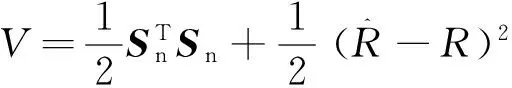
(16)

根据李雅普诺夫稳定性原理，要使系统稳定，须满足

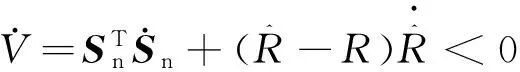
(17)

将式(15)代入式(17)可得

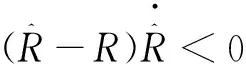
(18)

根据恒等式性质可知，式(18)可等效为下列两个方程

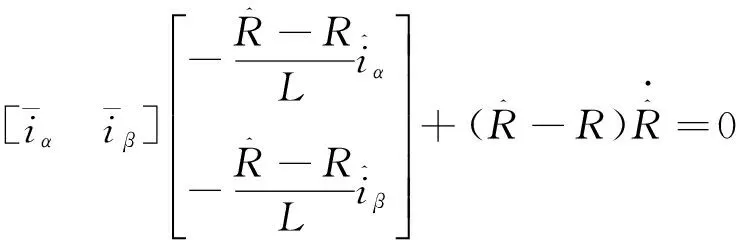
(19)

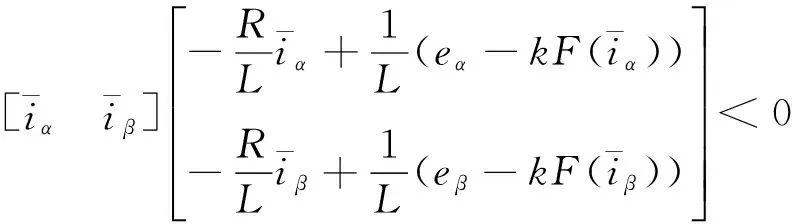
(20)

由式(19)可推导出估算的电阻微分方程为

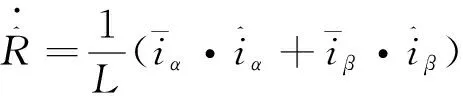
(21)

而式(20)可进一步写为

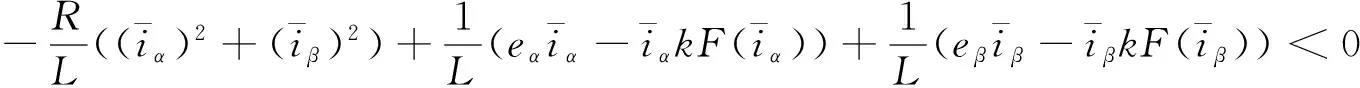
(22)

因Sigmoid函数F(x)的值域为[-1 1]，故可推导出滑模观测器增益k需满足

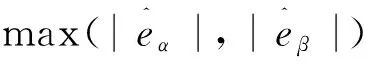
(23)

由式(10)和式(13)可推出

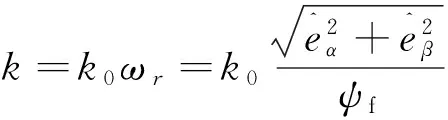
(24)

式中，k0>1，ψf<1，从而可得到

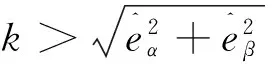
(25)

3 仿真与实验结果

为验证提出的定子电阻在线辨识的改进型滑模观测方法的性能，选取一台电动巴士驱动用的永磁同步电机作为研究对象，电机主要参数如表1所示。

表1 仿真实验用电机参数

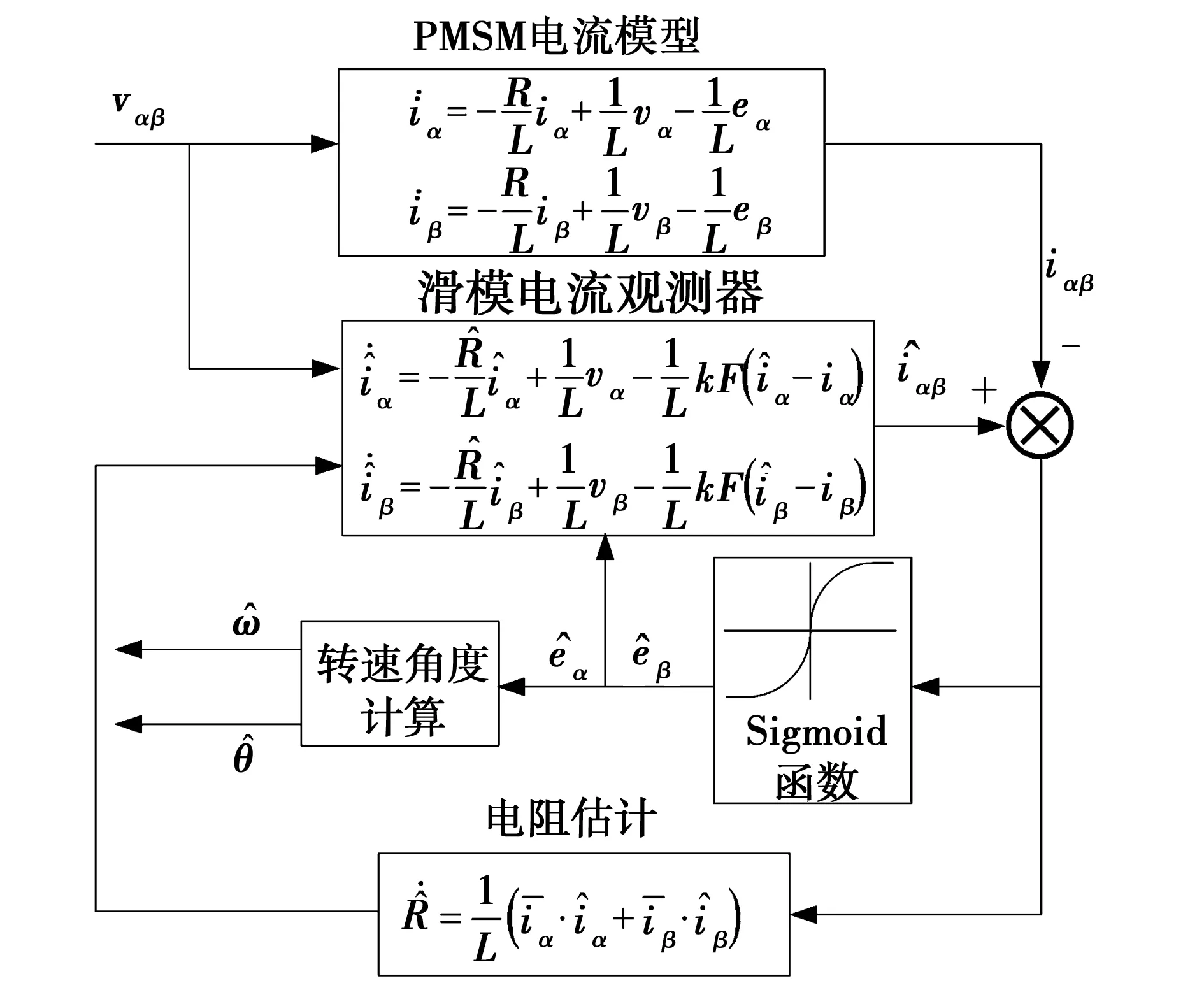
图4 电阻在线辨识的滑模观测器结构图Fig.4 Structure diagram of sliding mode observer with stator resistance identification online

3.1 仿真结果

在Matlab/SIMULINK环境下搭建永磁同步电机仿真模型进行仿真研究，系统采用id=0的矢量控制策略，速度环和电流环均采用PI控制，观测器分别采用传统滑模观测器和改进型滑模观测器，对其仿真结果进行比较分析。图5为系统矢量控制框图。

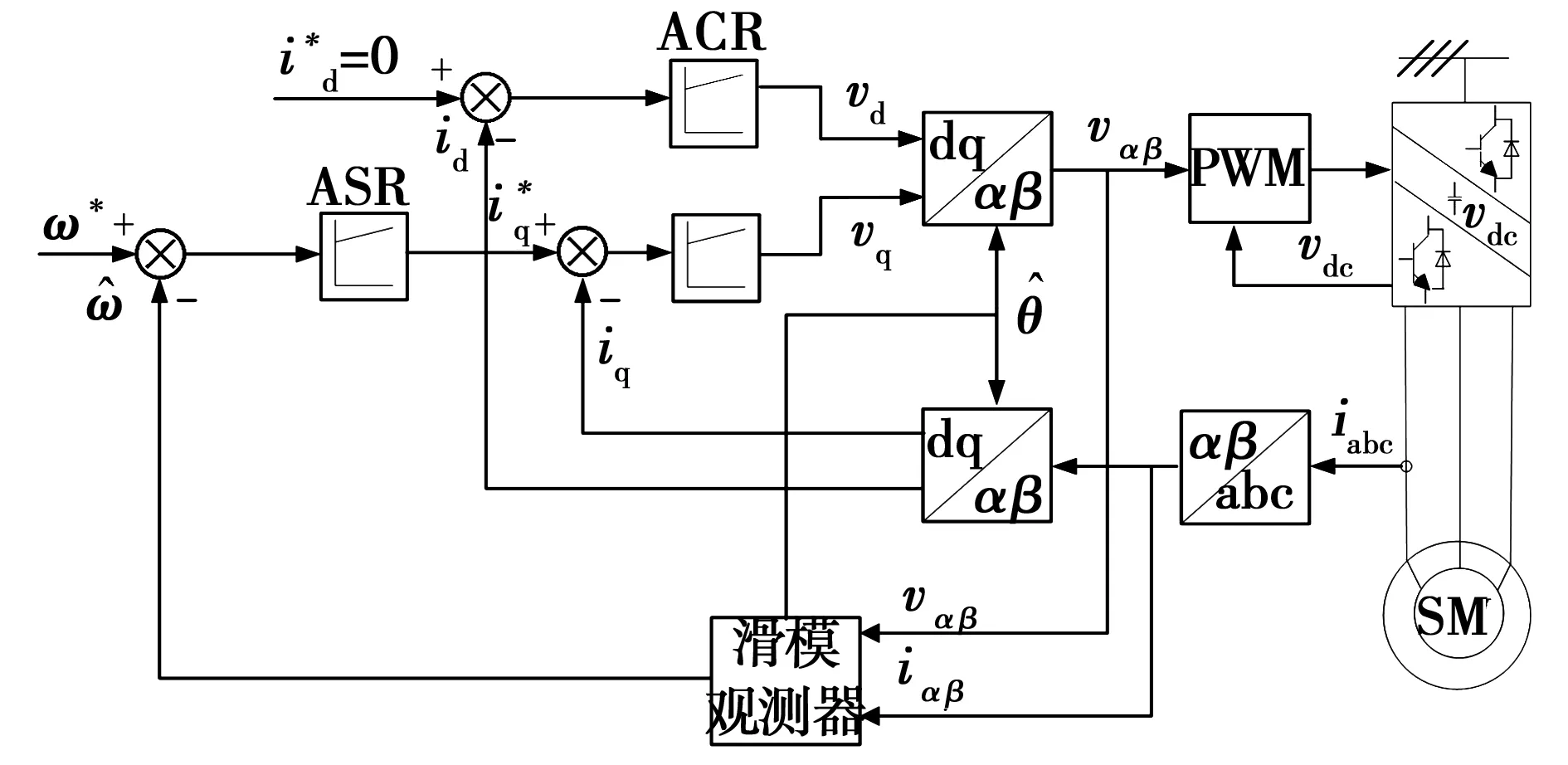
图5 PMSM无传感器矢量控制框图Fig.5 Block diagram of PMSM sensorless vector control

图6～图8为采用传统滑模观测器与改进型滑模观测器的对比仿真波形图。仿真时间为0～0.4s，电机初始转速设定为350r/min，在0.2s时给定电机的速度为1 500r/min。传统滑模观测器一阶低通滤波器的截止频率为1 500rad/s，滑模观测器的增益Ksw取300；改进型滑模观测器Sigmoid函数中参数A的值为5，滑模观测器的增益系数k0取1.1。

由图6～图8可以看出，在低速段传统方法估算得到的反电势信号包络线明显，获得的位置信号在起动阶段抖振比较严重，转速估算信号波动大且精度不高。采用无低通滤波器的Sigmoid函数后，可以得到比较理想的反电势估算波形，相比于传统滑模观测器，低速段的抖振现象得到改善，位置估算信号能够较好地跟踪实际值，得到的转速估算信号波形平整，与实际转速信号差异不大。

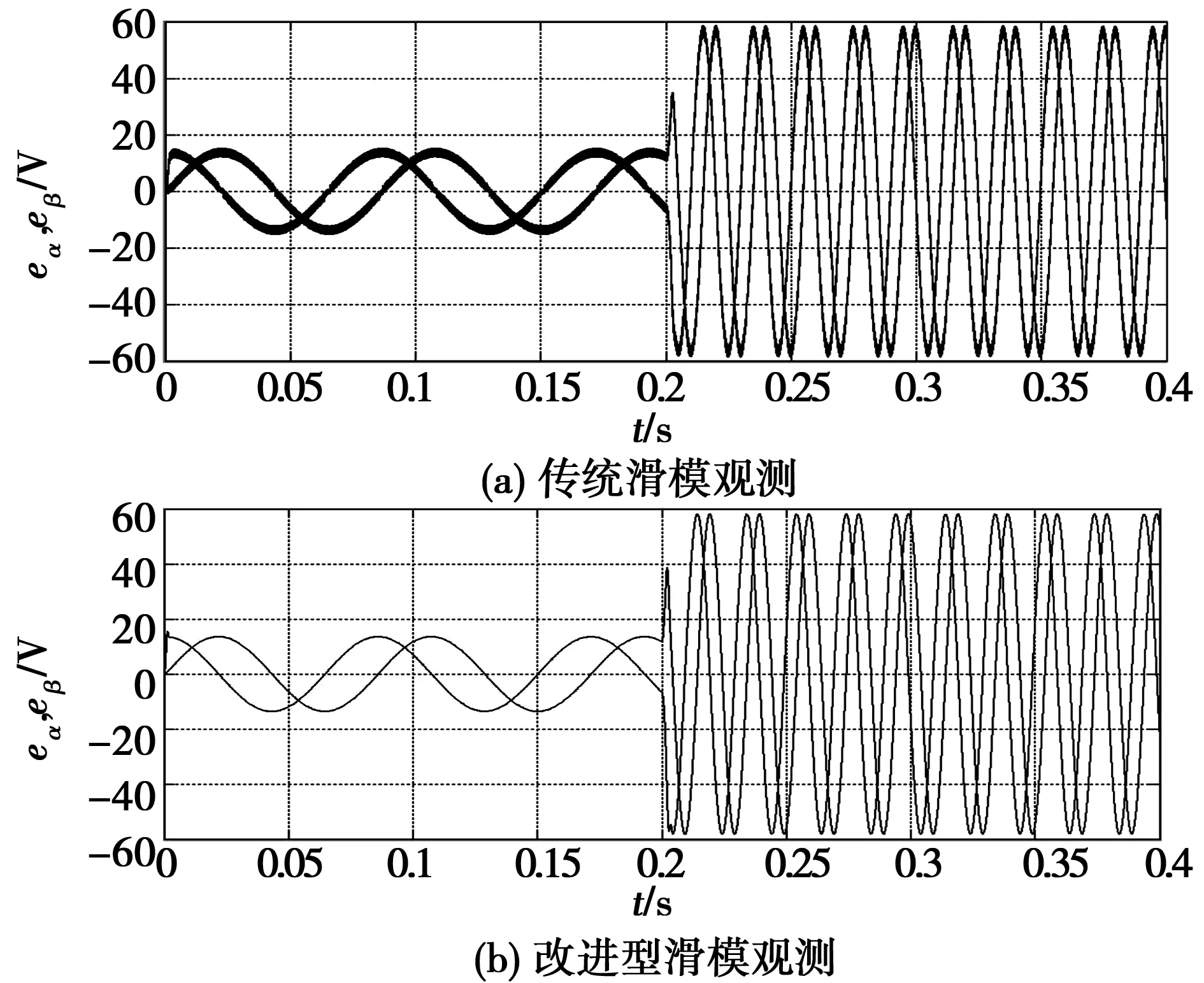
图6 反电动势波形图Fig.6 Waveform of back EMF

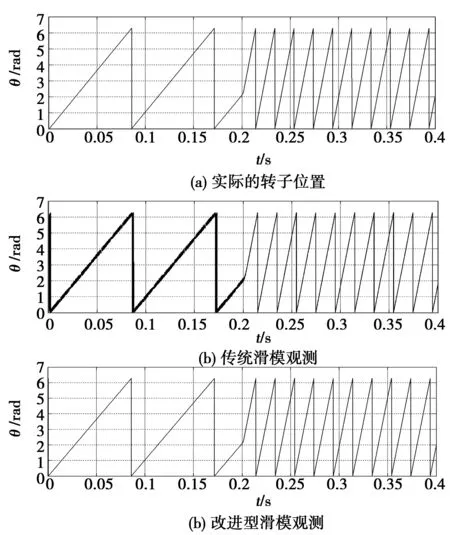
图7 转子位置波形图Fig.7 Waveform of rotor position

在电机的给定转速在0.2s由350r/min阶跃至1 500r/min后，随转速增大反电动势幅值也随之增大，但由于传统滑模观测器的增益保持不变，Sign函数的边界层厚度同样保持不变，高速运行时速度的估算误差在30r/min范围内；使用可变边界层厚度的Sigmoid的方法后，观测器增益k根据转速的大小来调节，使Sigmoid函数边界层厚度随转速变化而变化，高速运行时估算的转速波形明显得到改善，估算误差在5 r/min范围内。图9为电机在1 500 r/min运行过程中定子电阻增大为原额定阻值的1.25倍下的仿真波形图。

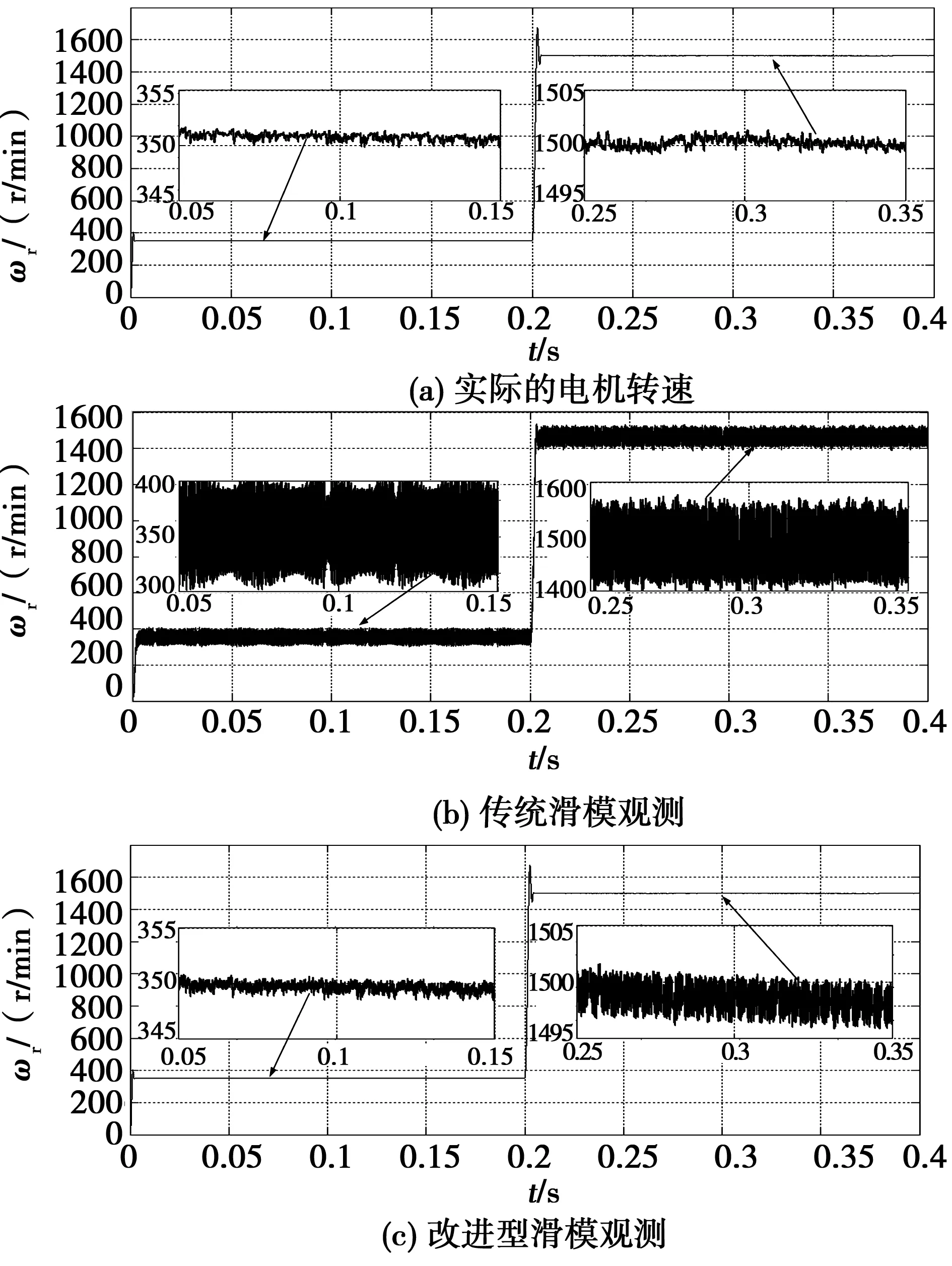
图8 电机转速波形图Fig.8 Waveform of motor speed

由图9(a)可知，定子电阻突变后，电阻在线辨识的方法在10 ms左右就能估算到定子电阻变化值，并根据估算的定子电阻值实时调整滑模观测器辨识模型，从而降低定子电阻变化对速度辨识造成的影响。由图9(b)可知，未加定子电阻辨识的方法在0.2 s定子电阻发生突变后，观测的转速受到了定子电阻变化的影响较大，波动范围为15 r/min；由图9(c)可知，加入电阻参数在线辨识的方法后，电机转速在电阻突变后波动范围为5 r/min，且在20 ms左右转速趋于稳定，保证了电机的正常运行，可见定子电阻在线辨识对于电阻变化时的电机无传感器运行效果明显。

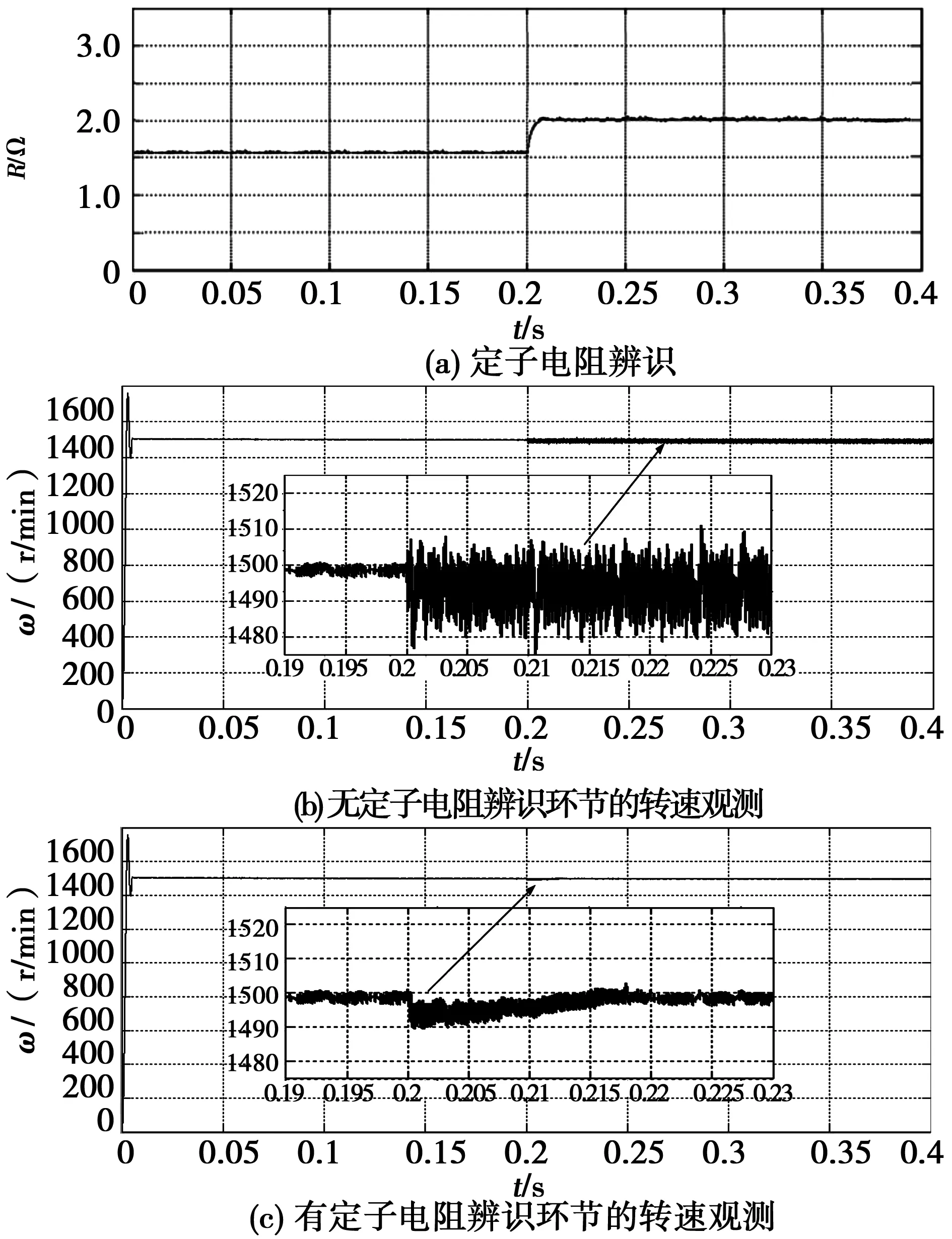
图9 电阻变化的速度波形图Fig.9 Simulation waveforms of motor speed with stator resistance change

3.2 实验结果

为进一步验证所提出方法的实际应用有效性，对表1所示电机进行实验研究。电机驱动系统供电中间直流母线电压为750 V，电机驱动逆变侧采用基于TMS320F28335DSP控制器和两电平IGBT主回路的磁场定向控制平台，开关频率设置为2.0 kHz。

受示波器采样通道的限制，考虑三相电流瞬时值之和恒定，仅对a相和b相电流进行了采样比较。图10为转速给定1 500 r/min，永磁同步电机负载运行时的稳态波形，其中图10(a)为传统滑模观测器测得的两相电流及转子位置与实际转子位置波形图；图10(b)为改进型滑模观测器后得到的相电流及转子位置和实际转子位置波形图。其中，θref为实际的转子位置，θest为测得的转子位置波形。由波形对比可知，相比于传统滑模观测器，改进型滑模观测器可以削弱抖振，更加准确地估算出转子位置。

为了验证改进型滑模观测器的动态性能，还进行了转速阶跃实验。图11为转速给定由350r/min阶跃至1 500r/min时的响应波形，图中ωref为角速度给定值，ωest为实际转子角速度辨识值。

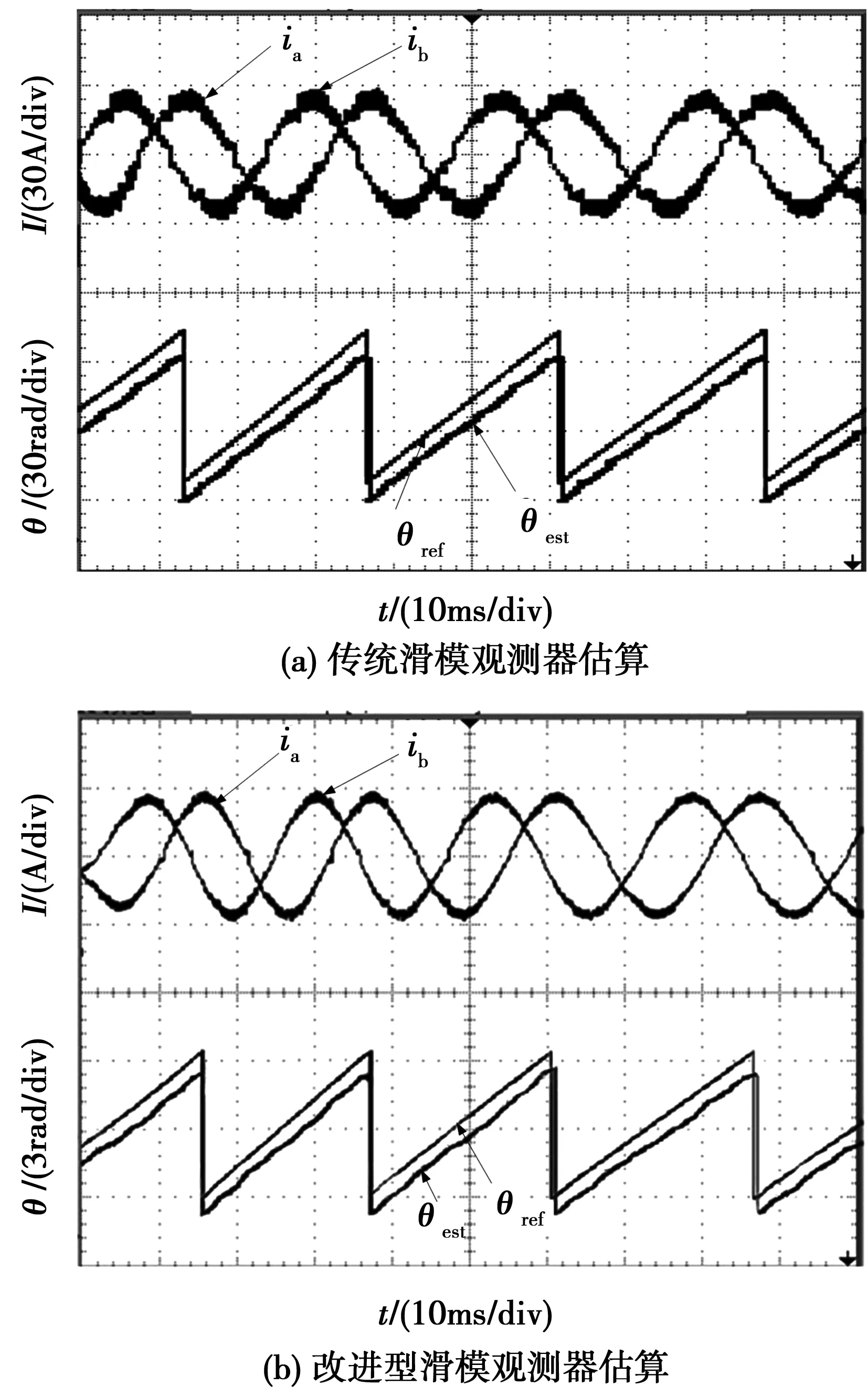
图10 电流与转子位置波形Fig.10 Waveform of currentand rotor position

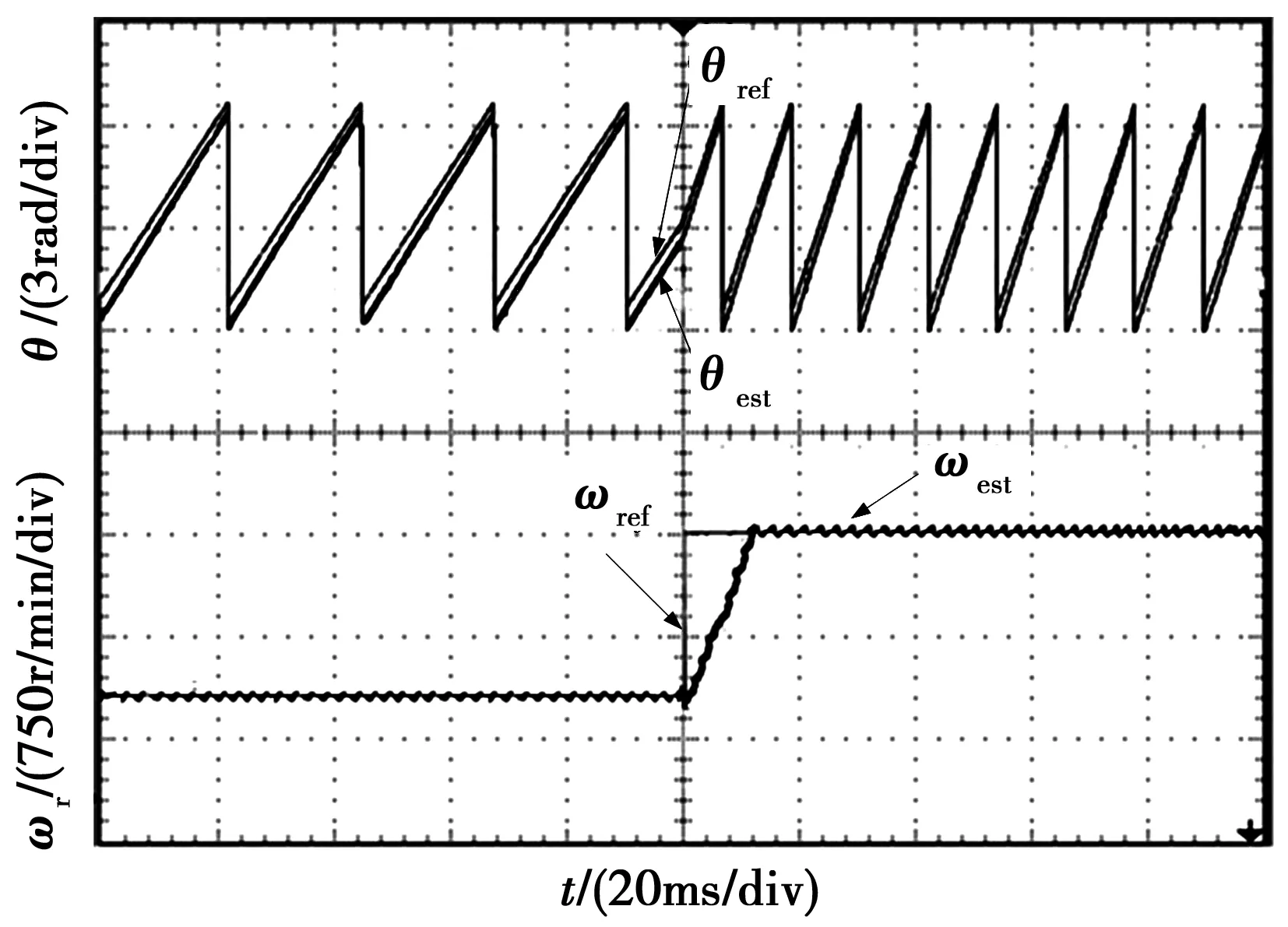
图11 速度阶跃下的动态响应波形Fig.11 Waveform of dynamic response

由图11可以看出，在电机转速给定阶跃变化时，改进型滑模观测器辨识得到的转子位置、转速信号都可以较好地跟踪实际信号，图中在转速估计值没有经过任何滤波处理时可见略有波动，但整体的抑制抖振效果良好。

4 结 论

本文在传统滑模观测器的基础上，考虑固有的抖振问题及电机定子电阻的影响，提出了改进的基于电阻在线辨识的PMSM滑模观测法，运用李雅普诺夫函数对其进行了稳定性证明，并进行详细的仿真与实验验证，得到如下结论：

1)在传统滑模观测器的基础上，以可变边界层厚度的Sigmoid函数取代Sign函数，消除低通滤波器及其相位补偿环节的同时，可以使观测器增益随速度大小动态调整，有效抑制了滑模观测的抖振现象并获得宽调速范围内的理想观测精度。

2)在改进后的滑模观测器中加入电阻在线辨识环节，利用李雅普诺夫函数设计了一种电阻参数在线辨识算法。通过对电阻的在线辨识，实时的去调整滑模观测器辨识模型，有利于提高系统鲁棒性。

3)基于改进后的方法进行的仿真与实验结果表明，与传统滑模观测器相比，基于电阻在线辨识的PMSM滑模观测方法可以有效地削弱系统抖振，降低了定子电阻参数变化对速度辨识精度的影响，提高了滑模观测器的精度，有利于对永磁同步电机的速度和位置的精确估计。而且由于算法与结构简单，有利于在数字控制器中实现。

[1] KUMAR J,KUMAR P S,RAMBABU M. Model reference adaptive controller-based speed and q-axis inductance estimation for Permanent Magnet Synchronous Motor drive by utilizing reactive power[C]// IEEE International Conference on Energy,Automation and Signal,2011: 1-6.

[2] FRENCH C,ACARNLEY P. Control of permanent magnet motor drives using a new position estimation technique[J]. IEEE Transactions on Industry Applications,1996,32(5): 1089-1097.

[3] ZHANG Shao,Tseng K J,Vilathgamuwa D M,et al. Design of a robust grid interface system for PMSG-based wind turbine generators[J]. IEEE Transactions onIndustrial Electronics,2011,58(1): 316-328.

[4] 郝雯娟,邓智泉,王晓琳. 基于增强型自适应观测器的永磁同步电机无速度传感器[J]. 电工技术学报,2009,24(3): 41-46. HAO Wenjuan,DENG Zhiquan,WANG Xiaolin. Enhanced adaptive observer for sensorless PMSM drive system[J]. Transactions of China Electrotechnical Society,2009,24(3): 41-46.

[5] 王高林,杨荣峰,李刚,等. 基于高频信号注入的IPMSM无位置传感器控制策略[J]. 电工技术学报,2012,27(11): 62-68. WANG Gaolin,YANG Rongfeng,LI Gang,et al. Position sensorless control strategy of IPMSM based on high frequency signal injection[J]. Transactions of China Electrotechnical Society,2012,27(11): 62-68.

[6] 张猛,肖曦,李永东. 基于扩展卡尔曼滤波器的永磁同步电机转速和磁链观测器[J]. 中国电机工程学报,2007,27(36): 36-40. ZHANG Meng,XIAO Xi,LI Yongdong. Speed and flux linkage observer for permanent magnet synchronous motor based on EKF[J]. Proceedings of the CSEE,2007,27(36): 36-40.

[7] 李冉,赵光宙,徐绍娟. 基于扩展滑模观测器的永磁同步电动机无传感器控制[J]. 电工技术学报,2012,27(3): 79-85. LI Ran,ZHAO Guangzhou,XU Shaojuan. Sensorless control of permanent magnet synchronous motor based on extended sliding mode observer[J]. Transactions of China Electrotechnical Society,2012,27(3): 79-85.

[8] 丁文,梁得亮,罗战强. 两级滤波滑模观测器的永磁同步电机无位置传感器控制[J]. 电机与控制学报,2012,16(11): 1-10. DING Wen,LIANG Deliang,LUO Zhanqiang. Position sensorless control of PMSM using sliding mode observer with two-stage filter[J]. Electric Machines and Control,2012,16(11): 1-10.

[9] 鲁文其,胡育文,杜栩杨,等. 永磁同步电机新型滑模观测器无传感器矢量控制调速系统[J]. 中国电机工程学报,2010,30(33): 78-83. LU Wenqi,HU Yuwen,DU Xuyang，et al．Sensorless vector control using a novel sliding mode observer for PMSM speed control system[J]. Proceedings of the CSEE,2010,30(33): 78-83.

[10] 刘昇,卢广山,徐瑜等. 基于改进型滑模观测器的PMSM无位置控制[J]. 南京航空航天大学学报,2013,45(4): 474-478. LIU Sheng,LU Guangshan,XU Yu,et al. Sensorless control of permanent magnet synchronous motor based on improved sliding-mode observer[J]. Journal of Nanjing University of Aeronautics & Astronautics,2013,45(4): 474-478.

[11] 陈振锋,钟彦儒,李洁. 嵌入式永磁同步电机自适应在线参数辨识[J]. 电机与控制学报,2010,14(4): 9-13. CHEN Zhenfeng,ZHONG Yanru,LI Jie. Online adaptive parameter identification for interior permanent magnet synchronous motor drive[J]. Electric Machines and Control,2010,14(4): 9-13.

[12] PIIPPO A,HINKKANEN M,LUOMI J. Adaptation of motor parameters in sensorless PMSM drives[J]. IEEE Transactions on Industry Applications,2009,45(1): 203-212.

[13] SEILMEIER M,EBERSBERGER S,PIEPENBREIER B. Identification of high frequency resistances and inductances for sensorless control of PMSM[C]// Sensorless Control for ElectricalDrives and Predictive Control of Electrical Drives and Power Electronics (SLED/PRECEDE),2013: 1-8.

[14] LIU K,ZHU Z Q. Online estimation of the rotor flux linkage and voltage-source inverter nonlinearity in permanentmagnet synchronous machine drives[J]. IEEE Transactions on Power Electronics,2014,29(1): 418-427.

[15] UTKIN V,GULDNER J,SHIJUN M. Sliding Mode Control in Electro-Mechanical Systems (Second Edition) [M]. London: Taylor & Francis,2009: 240-320.

[16] KIMHongryel,SON Jubum,LEE Jangmyung. A High-speed sliding-mode observer for the sensorless speed control of a PMSM[J]. IEEE Transactions on Industrial Electronics,2011,58(9):4069-4077．

[17] 刘金琨,孙富春. 滑模变结构控制理论及其算法研究与进展[J]. 控制理论与应用,2007,24(3): 407-418. LIU Jinkun,SUN Fuchun. Research and development on theory and algorithms ofsliding mode control[J]. Control Theory & Applications,2007,24(3): 407-418.

(编辑：刘素菊)

Study on improved sliding-mode control with resistance estimation of PMSM

ZHANG Yong-jun1， WANG Wei1， ZHANG Xiao-qing1， XIAO Xiong1， SHANG Jing2

(1.Institute of Engineer Technology,University of Science and Technology Beijing, Beijing 100083,China;2.CRRC Zhuzhou Institute Co.,LTD.,Zhuzhou 412001,China)

The stator resistance uncertainty and the inherent chattering of the traditional sliding mode observer exist in permanent magnet synchronous motor (PMSM) sensorless variable frequency speed control system.An improved sliding mode observer with online stator resistance identification was designed to optimize the performance of PMSM drive system.Based on the principle of the conventional sliding mode observer,a sensorless control strategy that substitutes a Sigmoid function for the Sign function with a variable boundary layer was proposed,which can dynamically adjust the observer gain according to the speed. In order to eliminate the effect of the uncertainty of the stator resistance on speed estimation and improve the accuracy of sliding mode observer,the algorithm identified stator resistance online which can help update the parameters of sliding mode observer by using the Lyapunov function. The results of simulations and experiments show that,compared with the traditional sliding mode,the proposed algorithm can suppress the chattering problem,enhance the robustness of speed estimation in the effect of the uncertainty of the stator resistance and thus estimate PMSM drive system with high accuracy.

permanent magnet synchronous motors; sliding mode observer; sigmoid function; stator resistance identification

2014-11-28

国家科技支撑计划项目(2012BAF09B02)

张勇军(1973—)，男，博士，副研究员，研究方向为新型控制系统理论、交流调速控制理论与电力电子应用等领域； 汪 伟(1994—)，男，硕士研究生，研究方向为直驱式永磁同步发电机及其控制； 张小庆(1989—)，男，硕士研究生，研究方向为永磁同步电机及其控制； 肖 雄(1989—)，男，博士研究生，研究方向为新型控制系统理论、电力电子技术与非线性控制； 尚 敬(1977—)，男，博士，高级工程师，研究方向为大功率变流系统与交流传动控制技术。

张勇军

10.15938/j.emc.2017.06.002

TM 351

A

1007-449X(2017)06-0010-08