异步电动机断条与静偏心复合故障的电流特征

田慕琴， 李双双， 宋建成， 吝伶艳

(太原理工大学 煤矿电气设备与智能控制山西省重点实验室，山西 太原 030024)

异步电动机断条与静偏心复合故障的电流特征

田慕琴， 李双双， 宋建成， 吝伶艳

(太原理工大学 煤矿电气设备与智能控制山西省重点实验室，山西 太原 030024)

为了研究笼型异步电动机断条和静态偏心复合故障特征，采用多回路数学模型和改进的绕组函数法对复合故障下的定子电流特征进行了机理分析和仿真研究。首先建立笼型异步电动机的多回路数学模型，通过改进的绕组函数法计算了笼型异步电动机复合故障下的电感参数，推导了复合故障在定子电流中产生的特定谐波频率计算公式，然后建立了笼型异步电动机正常状态和复合故障时的有限元仿真模型，通过仿真对理论结果进行了验证。结果表明，复合故障发生时定子电流中除存在单一断条和静态偏心故障的特征频率外，还会产生一系列附加谐波分量，理论分析与仿真结果相符。

笼型异步电动机；复合故障；转子断条；静态偏心；多回路模型；绕组函数法

0 引 言

笼型异步电动机广泛应用于工农业生产中，但驱动负载的多变性和工作环境的恶劣性经常会导致笼型异步电动机故障。由于笼型异步电动机长期运行过程中的频繁启动、制动和重载运行，使转子断条故障发生率高达10%，且80%的断条故障都会导致气隙偏心[1]。气隙偏心主要分为两种：静态偏心和动态偏心，如图1所示。静态偏心是指定转子不同心，转子以自身几何轴心为旋转轴，定转子间的最小气隙固定不变，这一般是由定转子铁心椭圆、加工不良以及安装误差等因素所造成。动态偏心是指定转子不同心，但转子以定子几何轴心为旋转轴，最小气隙随旋转位置而改变，这主要是由转轴弯曲、轴承磨损、安装不同心等因素所造成[2]。

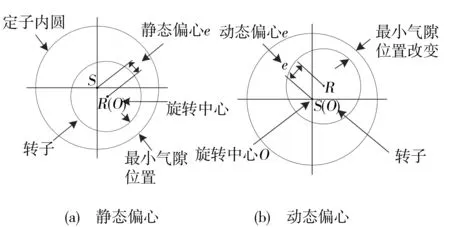
图1 基本气隙偏心类型Fig.1 Basic type of air gap eccentricity

针对笼型异步电动机转子断条故障时的定子电流特征，大量的研究工作表明笼型异步电动机发生转子断条故障时会在定子电流的基频和转子齿谐波(rotor slot harmonics，RSH)附近产生特征边频可以表示为[3-4]：

fb,LF=(1±2ks)fs,k=1,2，3…,

(1)

fb,HF=[h(1-s)±s±2μs]fs。

(2)

式中：s为转差率；fs为电源供电频率；h为谐波次数；μ=0，1，2，…为转速波动影响因子。

20世纪初国外出现了对气隙偏心的相关研究，80年代CameronJR，ThomsonWT等人[5-6]基于传统磁动势和磁导波的方法得到了当电机存在气隙偏心时，定子绕组中会形成一些与偏心有关的频率分量，可表示为

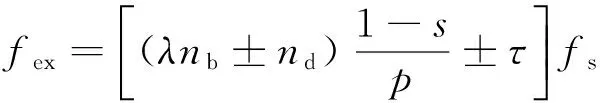
(3)

式中：λ=1,2,3,…；p为极对数；nb为转子槽数；nd为偏心阶数；静态偏心时nd=0；动态偏心时nd=1,2,3，…；τ=1,2,3…为电源谐波阶数。

转子断条和气隙偏心单一故障的诊断研究取得了诸多成果，而实际情况中两种故障往往是相互耦合，同时存在的。针对转子断条与静偏心复合故障，不少学者也做了相应研究。JawadFaiz[7]，FaizJ[8]等基于定子电流频谱分析对转子断条与静偏心复合故障下的转子断条数和静态偏心度进行了诊断，但只是分别检测单种故障特征。而实际情况中当两种故障同时存在时，复合故障特征往往并不是单一故障特征的简单叠加，而是按照一定规律耦合的。

在实际情况中，即使是全新的电动机也会因加工和装配等原因存在固有的偏心、不平衡等问题，因此很难获得纯粹的转子断条或静态偏心故障电动机，即使定制转子断条与静态偏心复合故障电动机也很难实现。而故障电机建模作为故障分析过程的第一步，可实现电机在不同运行下性能的准确分析。常用的笼型异步电动机故障建模方法有d-q模型、等效磁路法、绕组函数法、有限元法等。D-q模型忽略了离散绕组分布、齿槽效应、铁心饱和等影响，无法准确模拟笼型异步电动机的各种机械和电气故障[9]；等效磁路法和绕组函数法考虑了以上因素，建模更准确；绕组函数法[10]主要用于电机电感计算；等效磁路法[11]可直接分析大多数状态下的电机特性。2D和3D有限元法除上述因素，还综合考虑了集肤效应、转子斜槽影响及定子绕组的端部影响和涡流影响，是不同类型故障电机建模的有效工具[12]。

本文从耦合磁路角度通过多回路理论建立了复合故障在定子电流中产生的特定谐波频率计算模型，对复合故障下的典型故障特征与单种故障特征进行区分。基于Ansoft平台搭建了三相笼型异步电动机的有限元故障仿真模型，重点分析电动机的外部特性和内部磁场的瞬态变化过程，理想实现笼型异步电动机单一故障和复合故障的模拟，量化故障程度。

1 系统方程建立

分析电动机特性的最好方法就是获得其电磁场分布规律，但通过求解电磁场方程来分析电动机特性进而识别故障信号费时费力，而将电动机按照耦合磁路分组描述能够从另一个角度获得其运行特性。多回路理论突破了理想电动机的假设，从耦合磁路分组角度出发，按照定、转子的实际回路求取电压和磁链方程，能够计算、分析电动机定转子绕组内部和外部的所有回路电流，可以较好地解决气隙谐波磁场较强和绕组不对称问题[13]。

以三相笼型异步电动机为研究对象，假设三相定子绕组理想对称，供电电压三相平衡，电动机可看作多个相对运动回路组成的复合电路。若鼠笼电动机转子槽数为nb，则笼型异步电动机多回路模型具有三个独立的定子回路，nb+1个独立的转子回路，其中包括nb个相邻导条和端环段组成的转子回路和一个端环回路。

1.1 笼型异步电动机定转子回路

本文研究的笼型异步电动机为三相四极电机，定子槽数36，转子槽数26，定子绕组采取Y型联接，如图2(a)所示，转子回路电流取法如图2(b)所示。

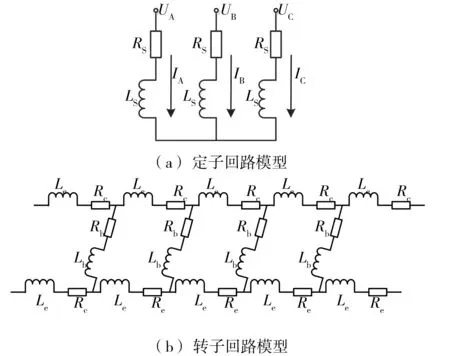
图2 笼型异步电动机定转子回路结构图Fig.2 Structure diagram of stator and rotor winding loop for squirrel cage induction motor

图2(b)中，Le和Re分别表示转子端部电感和电阻，Lb和Rb分别表示转子导条电感和电阻。由图可见，笼型异步电动机的多回路模型将定子一相并联支路作为一条支路，将转子相邻导条及其端环作为一条支路，然后根据定、转子回路的实际组成情况，建立有关定子回路和转子回路的方程。

1.2 笼型异步电动机多回路方程

根据图2可得定子电压和转子电压的多回路方程为：

(4)

(5)

式(4)和式(5)中的定子绕组和转子回路的磁链方程为

[ψsabc]=[Ls]·[Isabc]+[Msr]·[Irk]

(6)

[ψrk]=[Msr]t·[Isabc]+[Lrk]·[Irk]

(7)

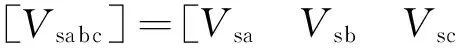
由式(4)和式(5)可以看出，定子磁链是定子电流与定子绕组自感耦合以及转子电流和定转子互感耦合的结果；转子磁链是转子电流与转子绕组互感耦合以及定子电流和定转子互感耦合的结果。当电动机结构不对称时，定子绕组的自感Ls和转子绕组的自感Lrk不再是常数，而是关于转子旋转角度θs的函数；定转子绕组之间的互感Msr是时变量，是关于转子旋转角度θs和时间t的函数。为方便后续计算，电感采用傅里叶级数形式表示。

2 复合故障下的电感参数计算

根据多回路数学模型中的电压方程(4)、(5)和磁链方程(6)、(7)能够计算分析电动机定转子绕组内部和外部所有回路电流，从而可分析复合故障在定子电流中产生的特征谐波分量。但多回路模型中的电压和磁链方程系数包括电阻和电感，而电感是时变的，难以计算。因此，求解方程的关键是电感参数的计算。

绕组函数法(windingfunctionmethod，WFA)和改进的绕组函数法(modifiedwindingfunctionmethod，MWFA)是基于电动机绕组和气隙参数来估算电感，是计算电感的有效方法。因为绕组结构决定了电动机磁动势和电动机的大部分磁导，在WFA和MWFA中对气隙偏心的影响可以通过修改气隙的磁导来建模进行分析。气隙对称时，WFA是适用的，而对于不均匀气隙，需要采用改进的绕组函数法(MWFA)[14]。

对于笼型异步电动机复合故障下的电感参数本文采用MWFA计算。假设笼型异步电动机满足以下理想条件：

1)忽略磁路饱和影响；2)铁心磁导率无穷大；3)磁通径向穿过气隙；4)涡流、摩擦、风阻损失都忽略不计；5)齿槽效应忽略不计。

电动机存在静态偏心时，气隙最小位置是固定不变的，气隙长度可表示为

g(θs)=g0(1+δscosθs)

(8)

式中：g0为气隙平均长度；δs为静态偏心度；θs为沿定子内圆的绝对角位置。

将磁导逆函数用傅里叶级数展开，取其前两项可得

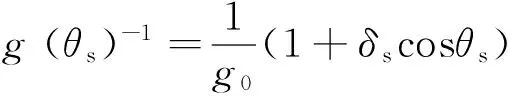
(9)

根据MWFA可得复合故障下笼型异步电动机任意2个定子回路“s”和转子回路“r”之间的互感计算公式[15]：

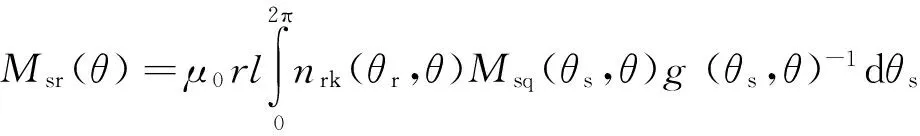
(10)

式中：r为气隙平均长度；l为铁心叠压长；θr为定子坐标下的转子角位置。

定子相“q”的匝函数为[15]：

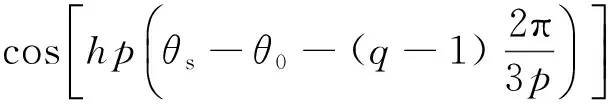
(11)

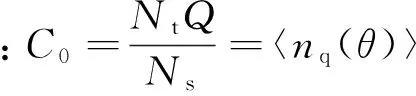
Msq(θs,θ)为“q”相改进的绕组函数[14]

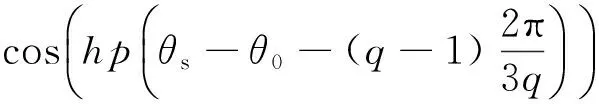
(12)

nrk(θr,θ)为第k个转子回路的匝函数[7]，能够反应绕组分布情况。

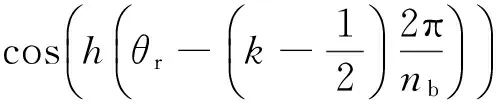
(13)

将(9)、式(12)、式(13)代入式(10)得定子绕组和转子回路的互感为式(14)Msr(θ)=Msr1+Msr2+Msr3=

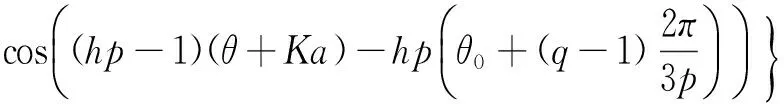
(14)

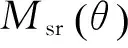
3 定子电流特征频率产生机理

3.1 转子电流

假设笼型异步电动机三相定子绕组对称，三相供电电压平衡，气隙中的三相合成磁动势会在转子回路中感应出sfs频率的电流。参照公式(7)，转子磁通分量在转子中感生电动势，进一步感生转子电流[16]。存在断条与静态偏心复合故障时，若仅考虑主频成分，则气隙磁动势在第k个转子回路中感应的电流公式为

[Irk]=[Irk1]+[Irk2]+[Irk3]。

(15)

(16)

(17)

(18)

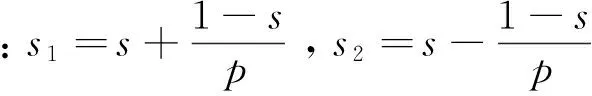
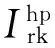
笼型异步电动机在转子断条故障情况下，式(16)、式(17)、式(18)中每个转子回路电流幅值互不相等，即

(19)

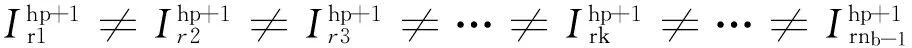
(20)

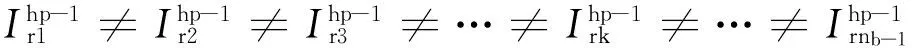
(21)

电动机断条与静偏心复合故障下的转子电流包括三部分，即[Irk1]、[Irk2]和[Irk3]。[Irk1]对应电机正常情况，[Irk2]和[Irk3]为转子电流中的不对称分量，这是由于电机静偏心故障所产生，而转子断条故障则会造成转子各回路中的各环路电流互不相等。

3.2 磁通导数

通过公式(4)，经Clarke变换的定子电压为

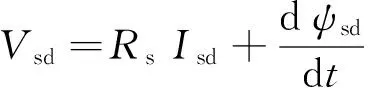
(22)

将公式(15)的[Irk]代入式(6)，得磁链导数为：

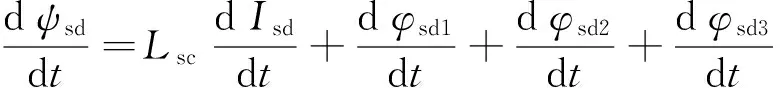
(23)

首先计算Msr(θ)与[Irk1]感生的磁链导数。为区分Msr和Irk两项的谐波次数，引入h1，其与h都表示谐波次数。

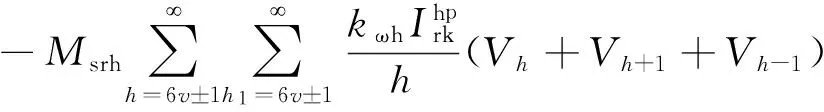
(24)

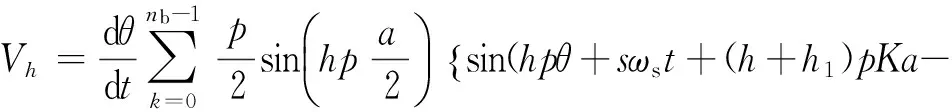
(25)

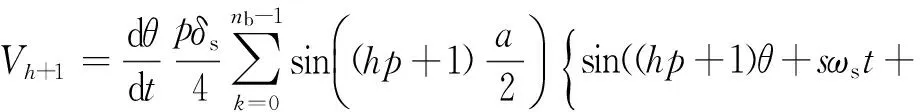
sin((hp+1)θ-sωst+((h-h1)p+1)Ka-

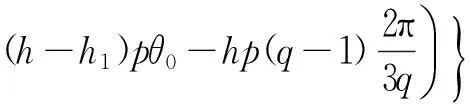
(26)

sin((hp-1)θ-sωst+((h-h1)p-1)Ka-

sin((hp-1)θ-sωst+((h-h1)p+1)Ka-

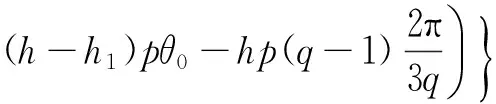
(27)

笼型异步电动机断条与静偏心复合故障时，其转子电流[Irk1]引起的磁链导数d[φsd1]/dt分为三项，即Vh、Vh+1和Vh-1。由式(26)、式(27)、式(28)可知d[φsd1]/dt的频率分量为hpθ±sωs、(hp+1)θ±sωs和(hp-1)θ±sωs。d[φsd1]/dt在定子中感应产生相同频率的电压分量，这些电压进一步感生同频率的定子电流。

3.3 定子电流特征频率

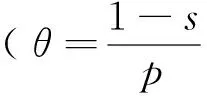
(28)

式中：h∈{6v±1}；v=0，1，2，3，…。

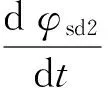
(29)

综上所述，断条与静态偏心复合故障在定子电流中产生的特征频率公式为

(30)

式中：h∈{6v±1}；v=0，1，2，3，…。

将上式代入不同的h值，与式(1)和式(2)转子断条特征频率以及式(3)静偏心特征频率相比较，可以发现转子断条与静偏心复合故障时定子电流中除存在单一断条和静态偏心的特征频率外，还会产生一系列附加谐波分量。

4 仿真模型

一般在电动机故障诊断研究中需要通过大量的破坏性试验来获得电动机故障数据，要耗费大量的人力物力，试验周期较长。而且由于制造工艺的缺陷，很难制造出理想的转子断条与静偏心复合故障的笼型异步电动机。因此，本文通过仿真建模来获得故障电动机数据，对理论分析结果进行验证。

为建立三相笼型异步电动机的有限元模型，需要对电机的转轴、定子和转子槽、定子和转子叠片等各部分进行建模，每个部分都要根据采用的实际材料赋予其物理特性，还需要根据实际情况设计各部分的尺寸参数。本文研究的三相笼型异步电动机仿真模型的主要外形尺寸及技术参数见表1。

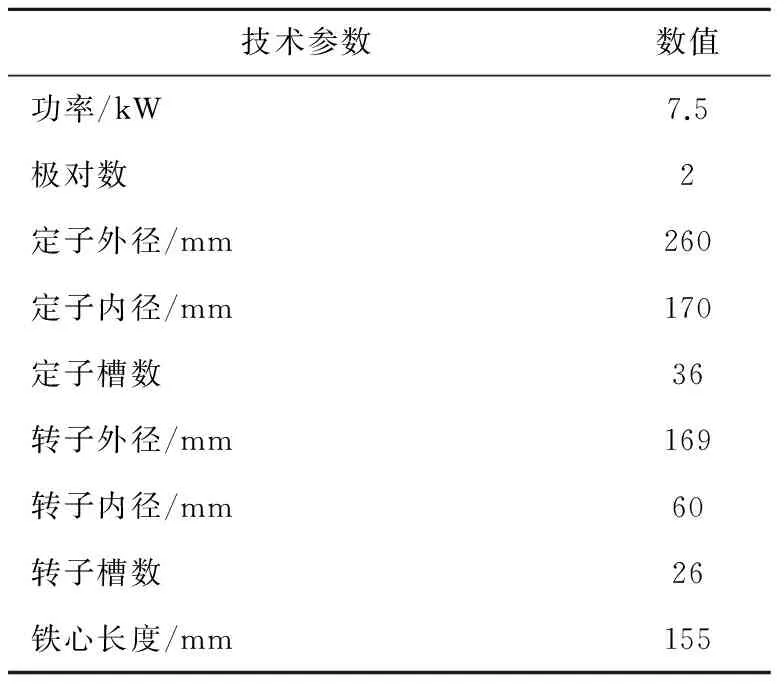
表1 电动机外形尺寸与技术参数

在Ansoft/Maxwell中根据表1中三相笼型异步电动机的基本参数建立2D几何模型。在瞬态磁场下对电动机进行求解。共搭建两个电动机模型，分别为正常电动机和复合故障电动机。在正常电动机模型上分别加入转子断条故障和气隙静态偏心故障。转子断条时断条电流并不为零，而是由于环流作用，断裂的导条上也会有微弱电流。在仿真时通过修改导条材料属性，将电导率设为极小值来实现断条故障。在正常电动机模型基础上设置定转子不同心，且以定子轴为旋转中心，以此实现模拟气隙静态偏心故障。仿真的复合故障电动机模型转子断条数为2，静态偏心度为20%。笼型异步电动机的仿真模型如图3所示，正常电动机和复合故障电动机的磁力线分布图如图4所示。

对比图4(a)和4(b)可见复合故障下笼型异步电动机的磁力线分布出现明显畸变，见图(b)中红色标注部分，断条处的磁力线分布密集，高度饱和，这是因为正常情况下转子回路中会感生出频率为sfs的三相对称电流，而当转子发生断条故障时，断裂导条中不存在滑差电流，无法产生转子导体的去磁效应，所以导致断条处的局部饱和。

图5给出了笼型异步电动机仿真模型在正常和复合故障(两根转子断条，20%静态偏心，)下的电流随时间的变化情况。可见，正常电动机的定子电流随时间的变化曲线为正弦波，而复合故障引起了定子电流的不平衡。按照THD(TotalHarmonicDistortion)计算方法，图5(b)的电流波形正弦畸变率为10.4%，波形畸变严重。

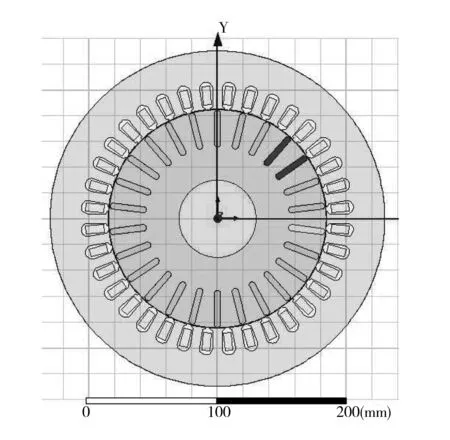
图3 复合故障的电动机仿真模型Fig.3 Motor simulation model of complex fault

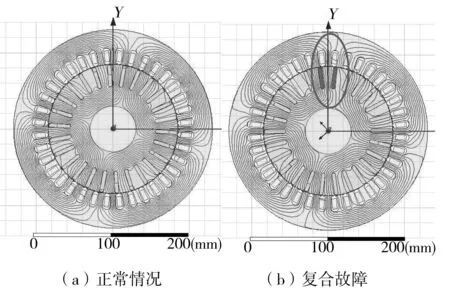
图4 笼型异步电动机磁力线分布图Fig.4 Magnetic field distribution diagram of induction motor

5 仿真结果分析

根据式(30)，断条与静态偏心复合故障时在定子电流中产生的一系列的特征频率，见表2(h=1,h=13)。其中h=1对应基频附近的特征边频分量，h=13对应转子齿谐波附近的特征边频分量。

分别对正常电动机和复合故障电动机仿真得到的定子电流进行快速傅里叶变换(FFT)，获得定子电流频谱分布图。为对表2中的频率分量进行更加深入的对比分析，重点研究频谱图中的低频(0～100Hz)和高频(550～700Hz)两个频段。图6为正常电动机电流低频段的频谱图；图7为复合故障电动机电流低频段的频谱图(为凸显其他边频，主频50Hz只截取了幅值的一部分)；图8为正常电动机电流高频部分的频谱图；图9为复合故障电动机电流高频部分的频谱图。

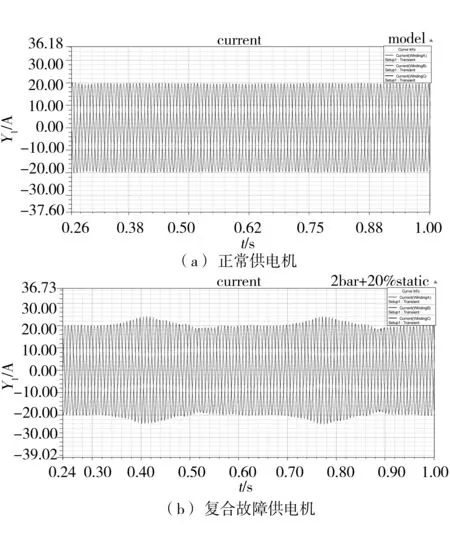
图5 笼型异步电动机复合故障定子电流波形图Fig.5 Stator current waveform of induction motor with complex fault

h=1h=13sfs24fr±fs(1±2s)fs25fr±fsfr±fs26fr±fs3fr±fs27fr±fs4fr±fs28fr±fs

从图中可以看出，图6中正常电动机的定子电流中只有50Hz工频；图7中复合故障电动机的基频附近存在明显的边频带。图7中，基频两侧的边频对应断条特征频率fb=(1±2s)fs，幅值分别为0.41A和0.48A；边频fr±sfs和3fr±sfs分别对应频率23Hz、26Hz、71Hz、74Hz，除fr+sfs幅值为0.12A外，其他边频幅值均小于0.8A；边频4fr±sfs由于幅值太小，基本可以忽略。对低频段的频谱分析可知，断条与静偏心复合故障在低频段会产生断条特征频率(1±2s)fs，还会产生fr±sfs和3fr±sfs的附加频率分量。

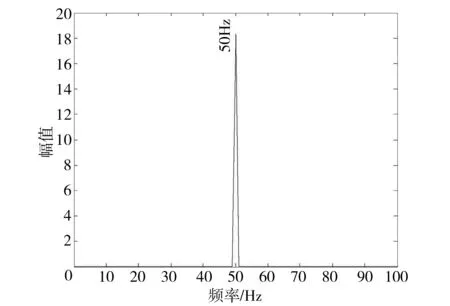
图6 正常电动机定子电流低频部分频谱图Fig.6 Frequency spectrum of the low frequency part of the stator current of healthy motor

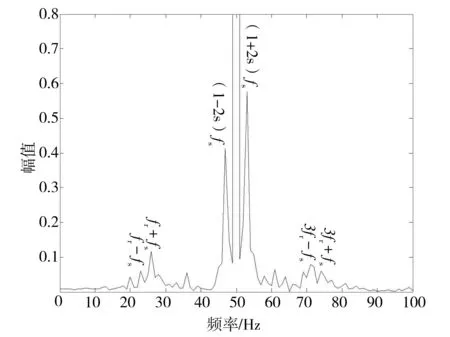
图7 复合故障电动机定子电流低频部分频谱图Fig.7 Frequency spectrum of the low frequency part of stator current of induction motor with complex fault

图8和图9分别为正常电动机和复合故障电动机定子电流高频部分在同一尺度下的频谱图。由图8可以看出，笼型异步电动机正常情况下高频部分只存在一些固有频率，且幅值非常小；由图9中可见笼型异步电动机复合故障时会在电流中产生若干高次谐波。图9中26fr±sfs对应公式(2)的转子断条特征频率630Hz和633Hz，24fr-sfs和28fr+sfs对应公式(3)的静态偏心特征频率582Hz和682Hz。对比两种故障的特征频率幅值可知，转子断条对转子齿谐波的影响更大。此外，转子断条与静态偏心复合故障在定子电流中还会产生其他特征频率24fr+sfs、25fr±sfs、27fr±sfs和28fr-sfs，但幅值相对较小。

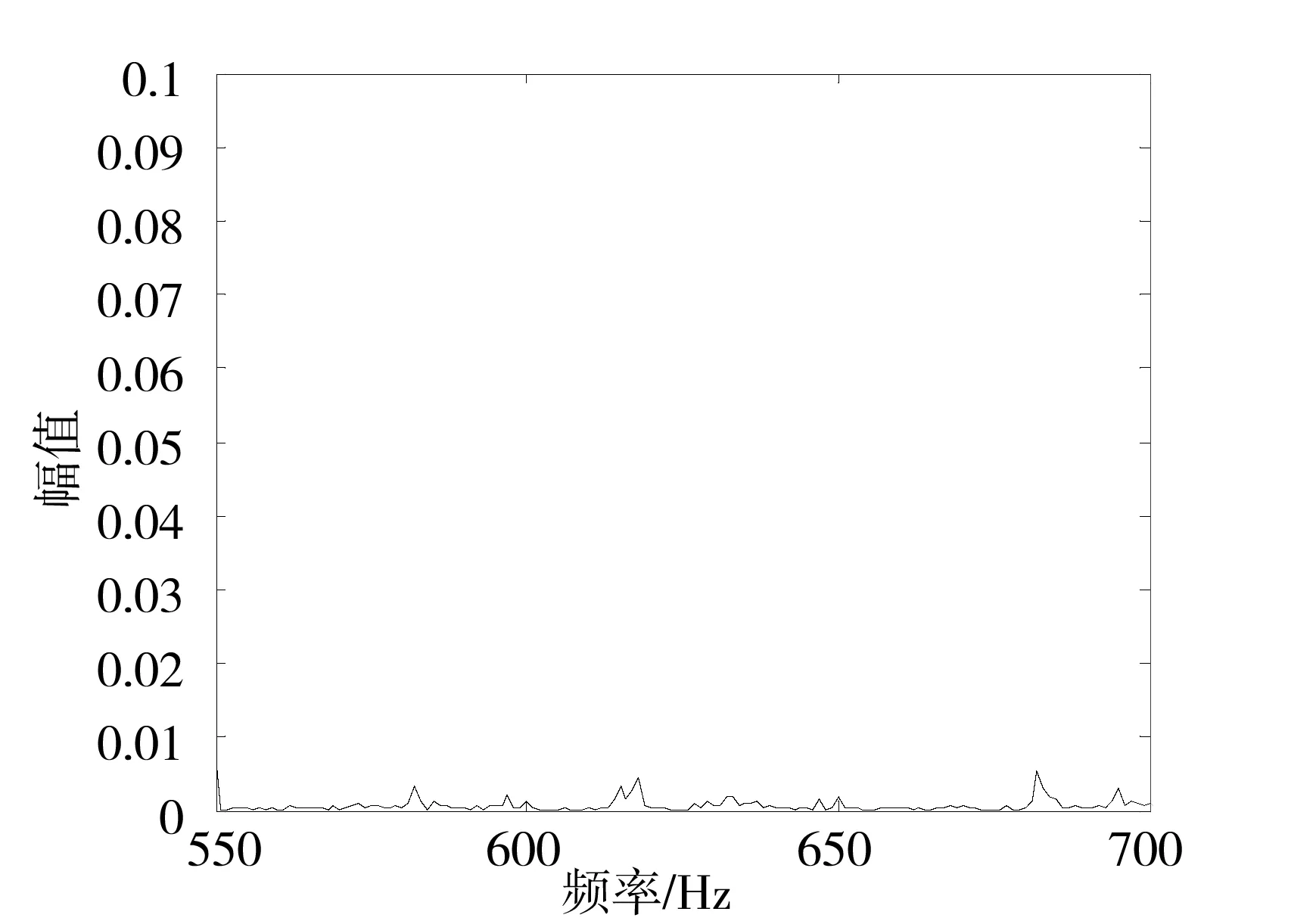
图8 正常电动机定子电流高频部分频谱图Fig.8 Frequency spectrum of the high frequency part of the stator current of healthy motor

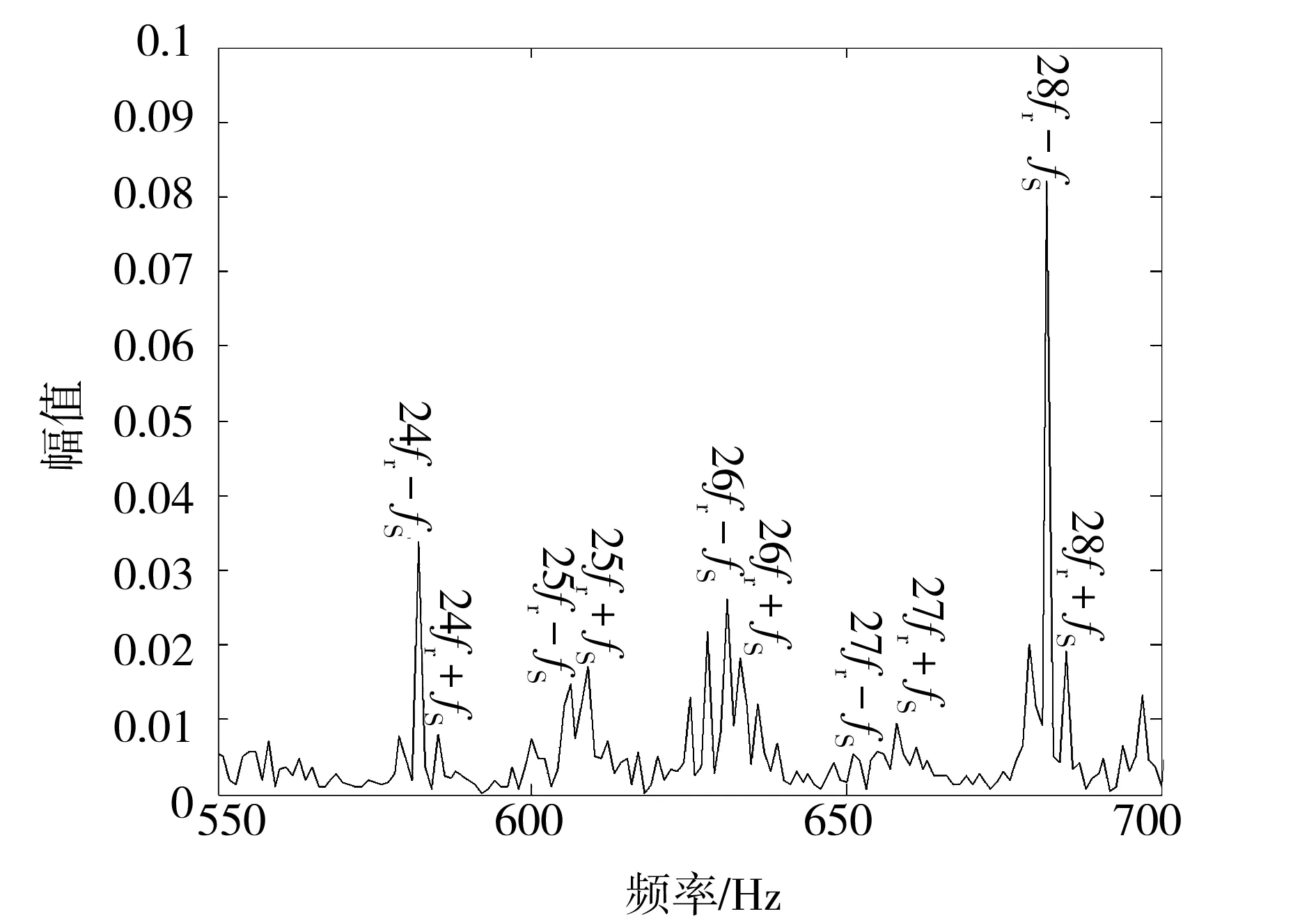
图9 复合故障电动机定子电流高频部分频谱图Fig.9 Frequency spectrum of the high frequency part of stator current of induction motor with complex fault

根据以上分析可以看出，断条和静态气隙偏心会导致气隙不平衡，进而改变气隙磁导。由于气隙磁导和气隙磁动势之间的相互作用，断条和静态气隙偏心会对基频电流和转子齿谐波产生影响，进而表现在定子电流的频谱变化中。而当断条和静态偏心两种故障同时发生时，各自引起的气隙不平衡在相互作用下形成新的不平衡状态，气隙磁导和气隙磁动势的改变是两种故障相互影响的直接结果，因此，在定子电流频谱中除包含单一故障特征频率外，还产生了一系列附加谐波频率。由于静偏心特征频率和附加谐波频率幅值较小，为实现复合故障可靠诊断，应采取措施放大这些频率分量。

通过以上分析可以看出仿真与理论分析结果完全吻合，式(30)可以为笼型异步电动机复合故障诊断提供判断依据。

6 结 论

本文针对笼型异步电动机转子断条与静偏心复合故障，采用多回路理论和改进的绕组函数法对定子电流的故障特征进行了理论推导，通过有限元仿真进行了验证分析。研究结果如下：

1)建立了笼型异步电动机转子断条与静偏心复合故障下的定子电流特征频率计算模型。结果证明复合故障时的定子电流特征不是单一故障特征的简单叠加，在两种故障相互耦合相互影响下，还会产生一系列的附加谐波分量，为复合故障诊断提供了新的诊断依据。

2)建立了笼型异步电动机转子断条与静偏心复合故障有限元仿真模型，该仿真模型有效的验证了理论推导结果的正确性，丰富了复合故障诊断的故障样本。

3)设计了定子电流仿真信号的频谱分析程序，通过实验发现转子断条故障对定子电流的影响远远大于静偏心故障。在故障诊断时应放大或偏移静偏心特征频率和附加谐波频率，以避免其被断条特征频率所淹没，对故障诊断算法的选取具有指导意义。

[1] 王惠中,张雨默,冯霞. 基于DSP电动机综合保护装置的设计[J].电力系统保护与控制,2011,39(3):105-108. WANG Huizhong,ZHANG Yumo,FENG Xia. Design of motor synthetic protection unit based on DSP[J].Power System Protection & Control,2011,39(3):105-108.

[2] 鲍晓华,吕强. 感应电机气隙偏心故障研究综述及展望[J].中国电机工程学报,2013,33(6):93-100. BAO Xiaohua,LÜ Qiang. Review and prospect of air-gap eccentricity faults in induction machines[J]. Proceedings of the CSEE,2013,33(6):93-100.

[3] 许允之,方磊,张建文. 基于最小二乘支持向量机的电机故障鉴别[J].电力系统保护与控制,2012(14):63-68. XU Yunzhi,FANG Lei,ZHANG Jianwen. Motor fault identification based on least squares support vector machine[J].Power System Protection & Control,2012,40(14):63-68.

[4] Khezzar A,Kaikaa M Y,El K O M,et al. On theuse of slot harmonics as a potential indicator of rotor bar breakage in the induction machine[J]. IEEE Transactions on Industrial Electronics,2009,56(11):4592-4605.

[5] Cameron J R,Thomson W T,Dow A B. Vibration and current monitoring for detecting airgap eccentricity in large induction motors[J]. Electric Power Applications,IEE Proceedings B[see also IEE Proceedings-Electric Power Applications],1986,133(3):155-163.

[6] Thomson W T,Barbour A. On-line current monitoring and application of a finite element method to predict the level of static airgap eccentricity in three-phase induction motors[J]. IEEE Transactions on Energy Conversion,1999,13(4):347-357.

[7] Jawad Faiz,Bashir Mahdi Ebrahimi. Determination ofnumber of broken rotor bars and static eccentricity degree in induction motor under mixed fault[J]. Electromagnetics,2008,28(6):433-449.

[8] Faiz J,Ebrahimi B M,Toliyat H A,et al. Mixed-fault diagnosis in induction motors considering varying load and broken bars location[J]. Energy Conversion & Management,2010,51(7):1432-1441.

[9] Cardoso A J M,Saraiva E S. Computer-aided detection of airgap eccentricity in operating three-phase induction motors by Park's vector approach[J]. 1993,29(5):897-901.

[10] Nandi S. A detailed model of induction machines with saturation extendable for fault analysis[J]. IEEE Transactions on Industry Applications,2004,40(5):1302-1309.

[11] Milimonfared J,Kelk H M,Nandi S,et al. A novel approach for broken-rotor-bar detection in cage induction motors[J]. Industry Applications IEEE Transactions on,1999,35(5):1000-1006.

[12] Faiz J,Ebrahimi B M. Anew pattern for detecting broken rotor bars in induction motors during start-up[J]. IEEE Transactions on Magnetics,2009,44(12):4673-4683.

[13] 李有军,王爱龙,熊光煜. 异步电机分析模型综述[J]. 电气技术,2007,11:8-11.

[14] Alnuaim N /,Toliyat H /. A novel method for modeling dynamic air-gap eccentricity in synchronous machines based on modified winding function theory[J]. Energy Conversion IEEE Transactions on,1998,13(2):156-162.

[15] Khezzar A,Hadjami M,Bessous N,et al. Accurate modelling of cage induction machine with analytical evaluation of inductances[C]// Industrial Electronics,2008. IECON 2008. 34th Annual Conference of IEEE. IEEE,2008:1112-1117.

[16] Kaikaa M Y,Hadjami M. Effects of the simultaneous presence of static eccentricity and broken rotor bars on the stator current of induction machine[J]. Industrial Electronics IEEE Transactions on,2014,61(5):2452-2463.

(编辑：刘素菊)

Effects of the mixed fault of broken bars and static eccentricity on current of induction motor

TIAN Mu-qin， LI Shuang-shuang， SONG Jian-cheng， LIN Ling-yan

(Shanxi Key Laboratory of Mining Electrical Equipment and Intelligent Control, Taiyuan University of Technology,Taiyuan 030024,China)

In order to study the characteristics of composite fault of broken bar and static eccentricity in squirrel cage induction motor,the multi-loop theory model and modified winding function method were used to analyze the characteristics of stator current under composite fault. The multi-loop theory model of induction motor was established,and the inductance parameter of induction motor was calculated by the modified winding function method. The finite element simulation model of induction motor under composite fault was built.The results show that there are not only the characteristic frequencies of single faults of broken bars and static eccentricity,but also a series of harmonic components of composite fault in stator current. The simulation results match the theoretical analysis.

squirrel cage induction motor; mixed fault; broken rotor bar; static eccentricity; multi-loop theory model; winding function method

2016-04-05

国家自然科学基金(U1510112)；国家自然科学基金(61472271)

田慕琴(1962—)，女，教授，博士生导师，研究方向为大型机电设备在线故障诊断和智能控制； 李双双(1989—)，女，硕士，研究方向为异步电动机故障诊断； 宋建成(1957—)，男，教授，博士生导师，研究方向为矿用智能电器技术和发电机故障诊断； 吝伶艳(1969—)，女，博士，副教授，智能电器技术。

田慕琴

10.15938/j.emc.2017.06.001

TM 307

A

1007-449X(2017)06-0001-09