泵站前池单排方柱整流措施数值模拟

夏臣智,成 立,赵国锋,于 磊,吴牧天,徐文涛

(扬州大学水利与能源动力工程学院,江苏 扬州 225000)



泵站前池单排方柱整流措施数值模拟

夏臣智,成 立,赵国锋,于 磊,吴牧天,徐文涛

(扬州大学水利与能源动力工程学院,江苏 扬州 225000)

为改善泵站前池内水流流态,基于Fluent软件,运用RNGk-ε模型对加单排方柱的正向进水泵站前池流态进行数值模拟,分析单排方柱的几何参数对前池流态改善的影响。结果表明:单排方柱具有分流效果,流经单排方柱的水流会向前池两侧分散,在单排方柱的后方形成漩涡。无整流措施时,泵站前池流态紊乱;通过在前池加设单排方柱可显著改善流态;单排方柱宜布置在前池前中部,不宜布置在两侧回流区内;方柱宽度越小,分流作用越小,行近流速分布越不均匀。

泵站;前池;整流措施;方柱;流态;数值模拟

立柱是一种被用于泵站前池内流态改善的工程措施,周济人等[1]对此进行了物理模型试验,并介绍了立柱和底坎组合在泵站前池流态改善中的作用。此后,罗缙等[2]在火(核)电站循环水泵房前池中也采用了立柱和底坎组合的整流措施,取得了较好的整流效果,并经模型试验得到验证。朱红耕[3]通过模型试验分析了水位对立柱整流的影响。罗灿等[4]将立柱与隔墩以及隔板组合用于侧向进水泵站的流态改善。上述研究表明,立柱在前池流态改善中有良好的作用。然而,对于单排方柱及其布置方法在泵站前池内的整流机理的研究较少。

数值模拟方法在对泵站前池流态改善研究中被广泛采用。刘超等[5]采用数值模拟方法对取水前池内流态改善进行了研究,计算结果与试验十分吻合。于永海等[6]采用VOF方法,基于Realizablek-ε紊流模型对泵站前池导流板整流措施进行了数值模拟研究。罗灿等[7]基于N-S方程和Realizablek-ε紊流模型,模拟了正向进水前池中无任何措施和增设底坎整流措施的流态。

本文基于Fluent软件模拟了单排方柱的整流效果,分析研究单排方柱在不同位置和几何参数下对改善前池流态的影响。

1 前池及单排方柱参数

所研究的泵站进水前池为正向扩散前池(图1),包括两孔涵洞、前池、进水池(1～10号)和吸水管。前池相关参数包括前池长度L0、前池宽度B0和吸水管直径D0，单排方柱的相关参数包括方柱宽度B1、单排方柱距进水池的长度L1和方柱的数量N。图1中断面3为计算时站前行近流速取值断面,距进水池0.438D0。各机组的站前行近流速取测速断面上正对吸水管中心测线上的平均速度。断面1和断面2为前池内水力损失的计算断面。

图1 泵站计算模型

2 数值计算方法

2.1 流体控制方程及边界条件

泵站涵洞、前池和进水池内的水流流动特性为三维不可压黏性流动,其流体动力学控制方程包括连续性方程和动量守恒方程[8]:

(1)

(2)

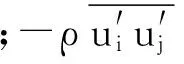
进口边界取在涵洞进口,设置为质量流量进口,以避免网格划分密度不均引起的计算误差[9]。出口边界取在进水池出水管出口,设置为静压出口。各固壁面采用壁面函数处理。由于水位变化不大,自由液面采用刚盖假定处理[10]。

2.2 网格划分

对前池和涵洞采用结构网格进行划分,对进水池采用非结构网格划分。全局单元最大尺寸为0.02 m,加密尺寸为0.01 m。对研究对象前池划分了不同数量的结构网格,网格节点数量在9.7万～29.3万。通过计算,前池网格数量为21.8万时,可满足网格无关性检验要求。计算网格如图2所示。

2.3 湍流模型选择

泵站内流动一般为高雷诺数的湍流流动,特别是前池内水流的扩散流动,往往存在边壁脱流和大尺度回流的状况,采用两方程k-ε模型较为合适[11]。在对泵站前池进行计算时,有选用RNGk-ε模型的[12],也有选用Realizablek-ε模型的[13]。本文对比了上述两种两方程k-ε模型对计算结果的影响,并与文献[11]及[14]试验结果进行了比较。图3为泵站站前行近流速分布,两种湍流模型的计算结果与试验值[11]分布趋势相近,泵站中间机组前的流速大,两侧机组前的流速小,边侧机组前的行近流速为负值,表明前池两侧边壁处存在回流区。图4为RNGk-ε模型和Realizablek-ε模型前池0.5H(H为水深)截面的流速分布,可见两种模型均能计算出前池两侧存在回流区,但是RNGk-ε模型计算结果显示,前池中部流速较大,两侧存在大小相近的回流区,与文献[14]更为接近。因此采用RNGk-ε模型对前池流态进行模拟。

图2 计算区域网格

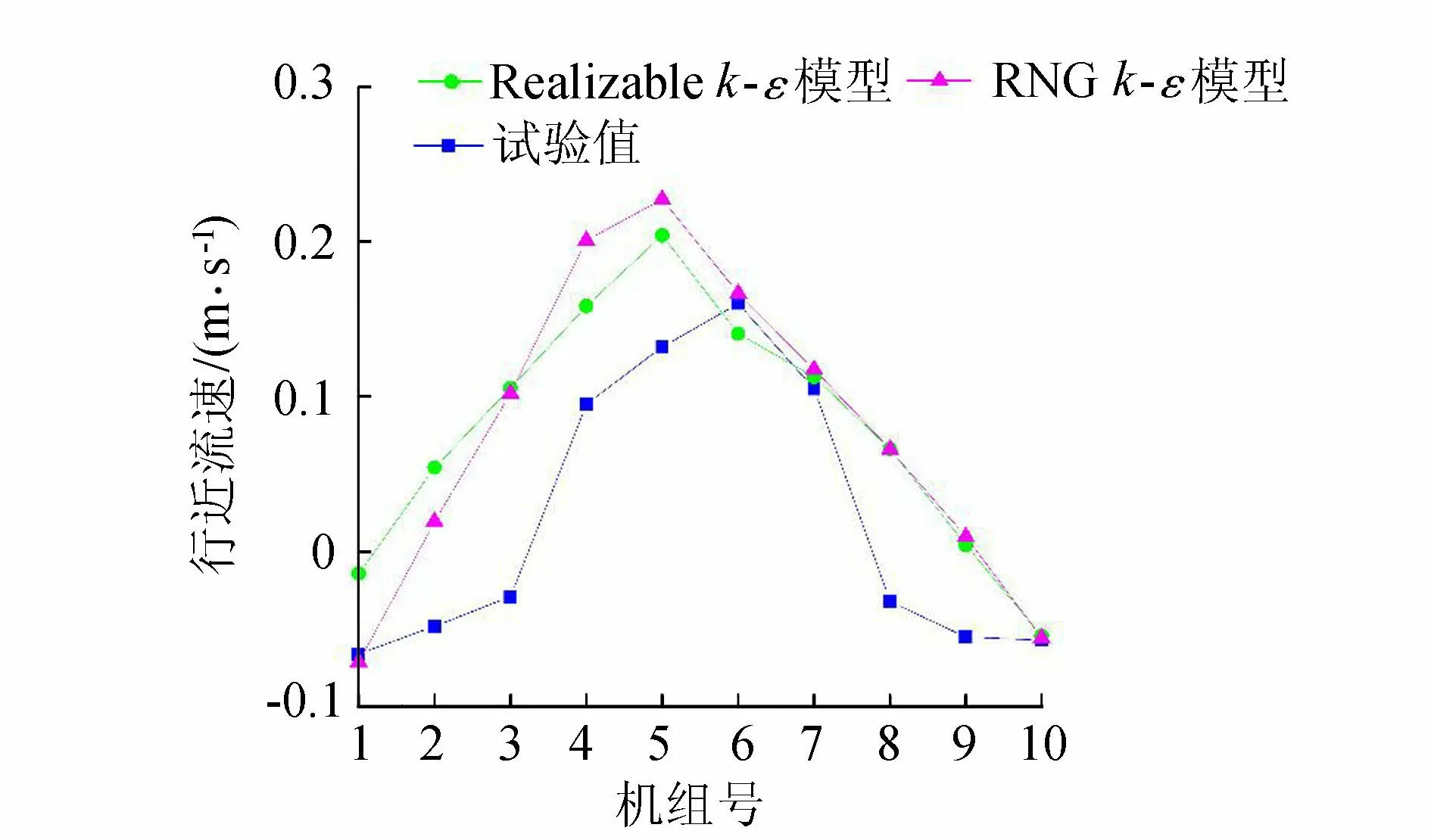
图3 站前行近流速分布

图4 前池0.5H截面流速分布对比(单位：m/s)

3 研究方案

为研究方柱的几何参数和布置形式对前池内流态的影响,设计7个方案(表1)来分析方柱的布置位置(方案1～3)、方柱宽度(方案1、4、5)和方柱数量(方案1、6、7)对前池内流态的影响。设计无整流措施方案(方案0)作为对照方案。方柱的具体布置形式如图5所示。

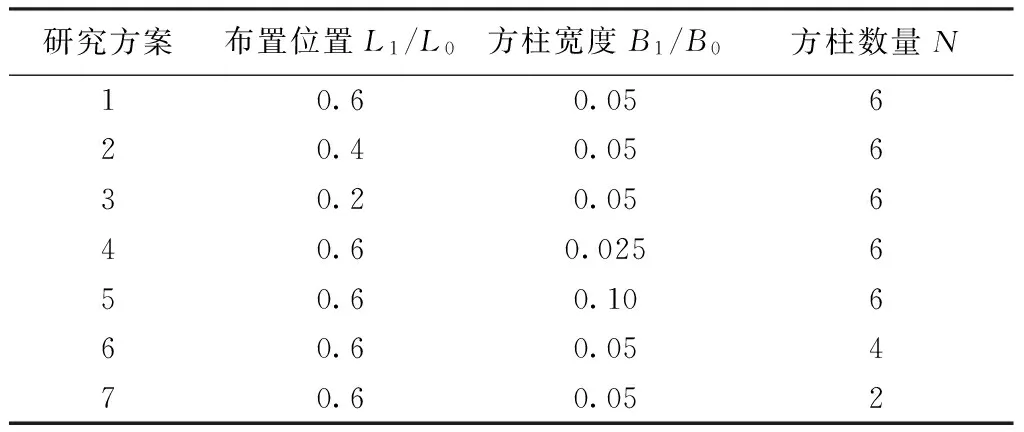
表1 研究方案

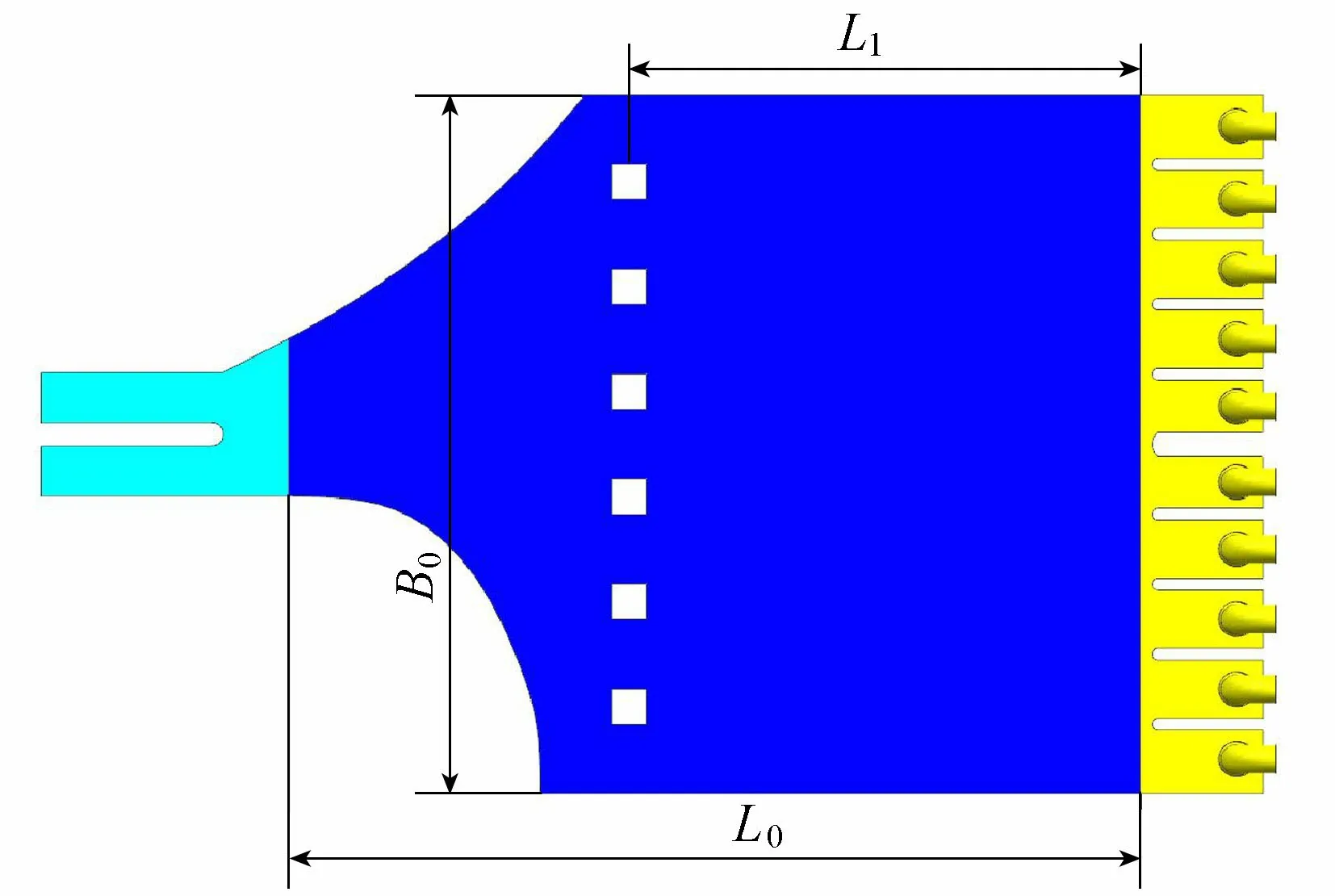
图5 泵站前池及方柱布置形式及参数

4 计算结果分析

4.1 无整流措施的前池流态

图6 无整流措施前池内流线(单位：m/s)

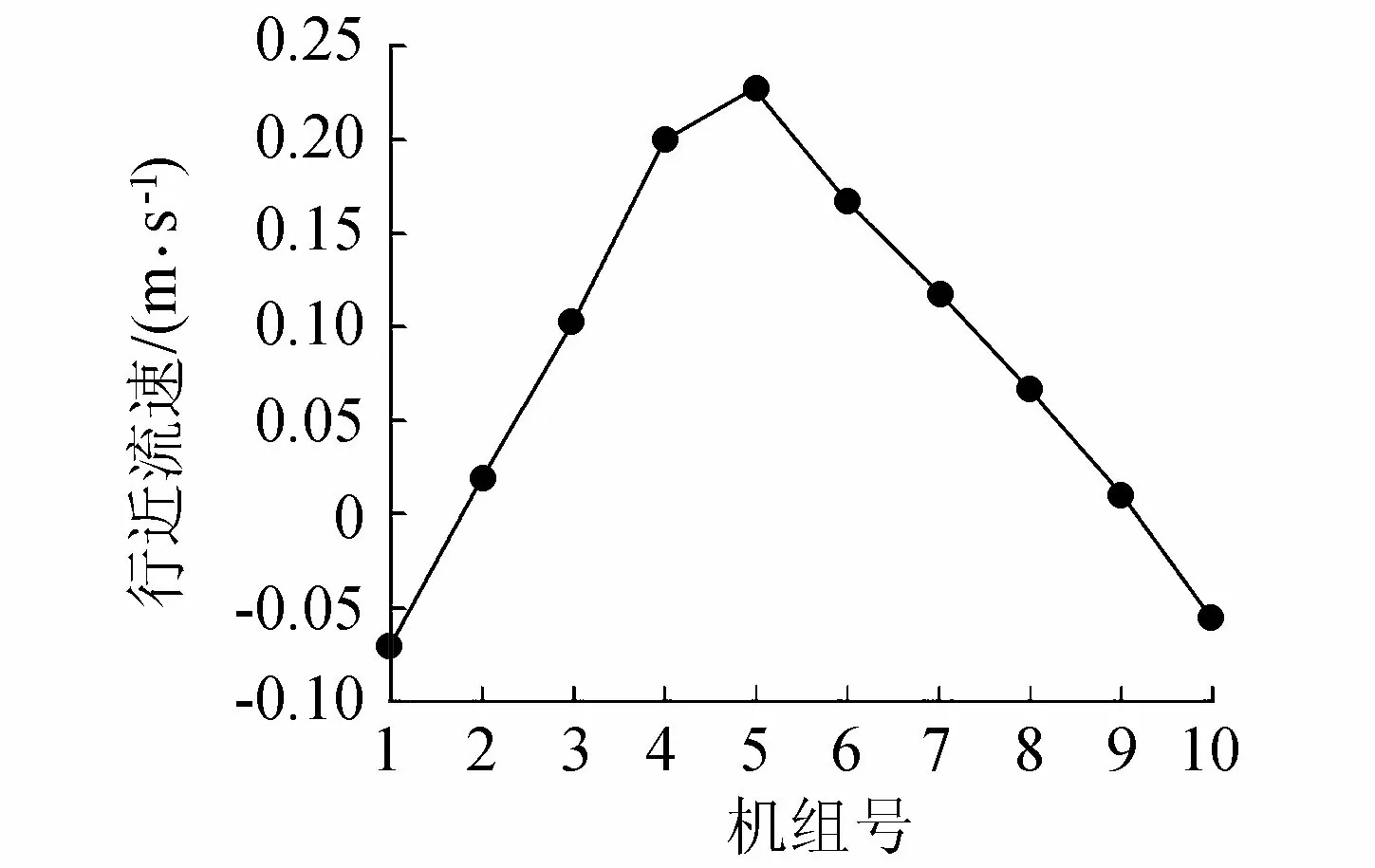
图7 无整流措施站前行近流速分布

图6为无整流措施的前池内流态,图7为无整流措施各机组站前行近流速分布。无整流措施的前池流态不良,两边壁侧有大范围的回流区,回流区的范围与前池长度近乎相等。由于前池两侧回流区逼近进水池,断面3的行近流速分布很不均匀,中间流速大,两侧流速小。

4.2 单排方柱位置对前池流态的影响

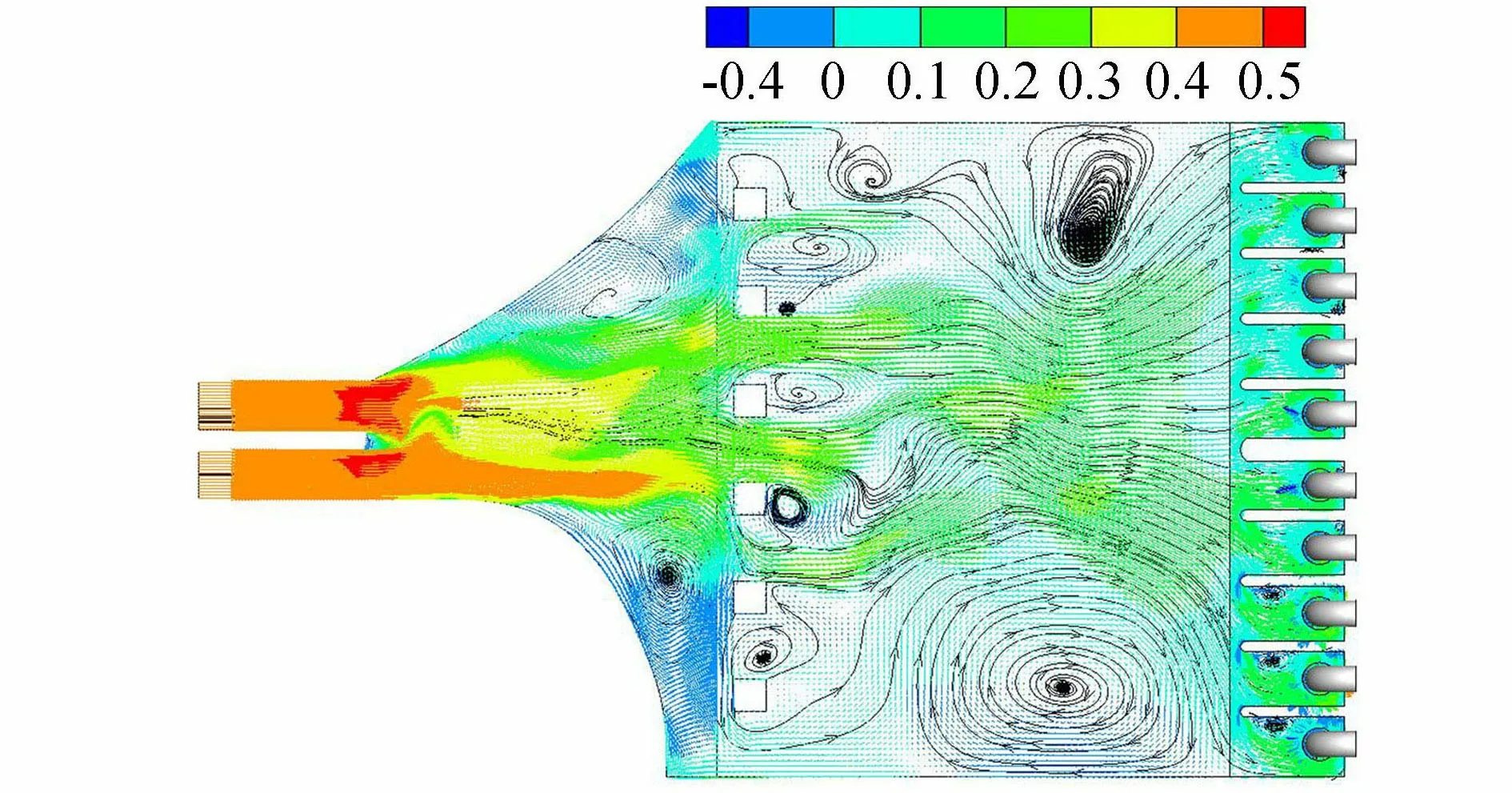
图8 方案1前池0.5H截面流速分布(单位：m/s)

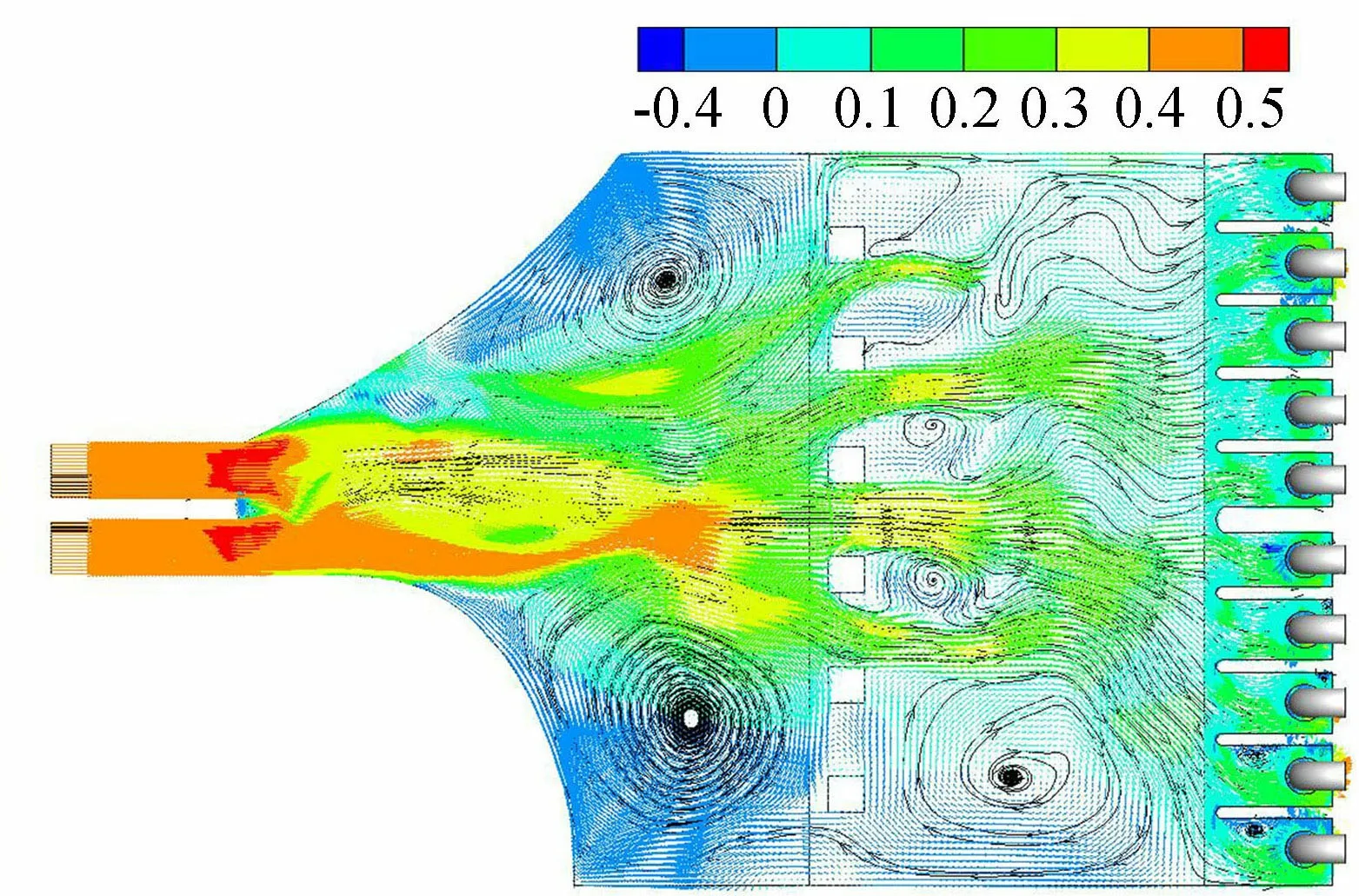
图9 方案2前池0.5H截面流速分布(单位：m/s)

图10 方案3前池0.5H截面流速分布(单位：m/s)

图8～10为方案1～3的前池内流态,显示加入方柱后前池内流态发生明显的改变,方案0中主流在前池中间的流态得到改善,前池两侧的大范围回流区被消除。方柱在其中起到阻水分流的作用,同时流体流过方柱后会在其后部形成卡门涡,而多个方柱后方的流场会形成复杂卡门涡场,流体间发生更强烈的能量交换,使得方柱后的水流流速得到进一步的调整。但是方柱后水流的能量交换和流速调整是需要空间的,从方案1～3的流态可以看出,如果方柱距离进水池过近,方柱后的涡场反而会进一步影响机组的行近流速。与方案2和方案3相比,方案1中间机组(3～8号)前的行近流速波动较小,分布更为均匀,方柱整流效果较好(图11)。在前池内采用方柱进行整流时,推荐方柱布置位置在前池扩散段末端。

图11 不同方柱位置站前行近流速分布

4.3 单排方柱宽度对前池流态的影响

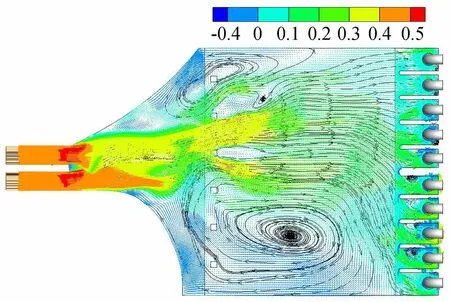
图12 方案4前池0.5H截面流速分布(单位：m/s)

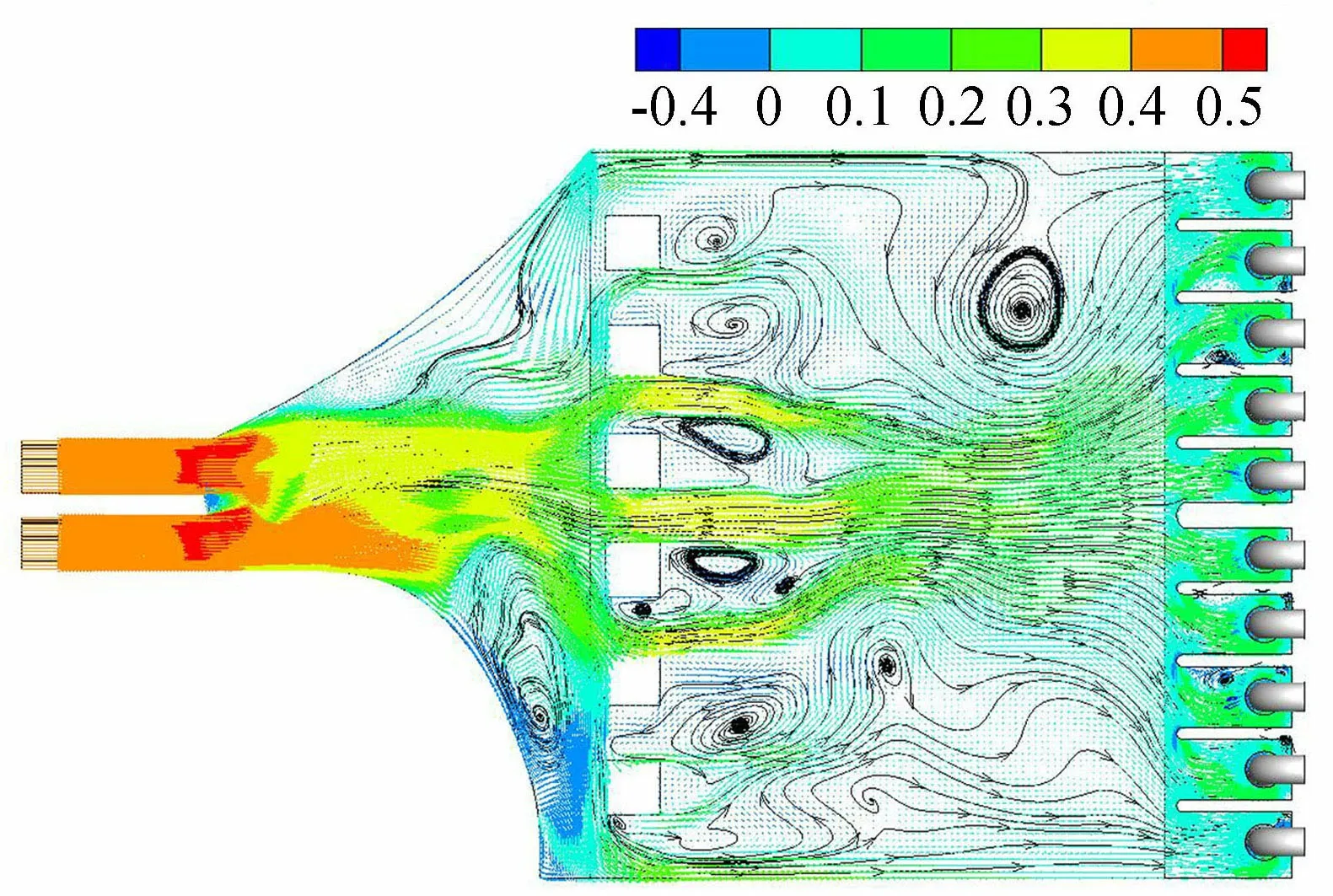
图13 方案5前池0.5H截面流速分布(单位：m/s)

图12、13为方案4和方案5的前池内流态,改变方柱的宽度,对前池内流态调整也有明显的影响。方柱宽度过小,则其阻水分流的效果就不明显,其柱后的水流能量交换效果也不太好,方案4前池一侧仍存在较大的回流区,影响到该侧机组的进水流态。方柱宽度增大时,其阻水分流效果明显。但是方柱间的距离随着方柱的宽度变大而变小,使得水流在流过方柱后,流速变大,回流区发生于前池两侧靠近进水池的位置,影响边侧机组的流速。与方案0相比,方案4、5的边侧机组流速仍然较小(图14),即使增大方柱的宽度也不能很好地改善边侧机组的进水流态。

图14 不同方柱宽度站前行近流速分布

4.4 单排方柱数量对前池流态的影响

考虑到前池两侧水流流速较小,若在前池边侧设置方柱,水流流速将进一步降低,对边侧机组的进水流态改善效果不佳,所以在方案1的基础上,从边侧起对称减少方柱的数量(方案6和方案7)。图15、16分别为方案6、7的前池内流态。方案6、7的回流区位置均在前池的前中部,与进水池相距较远,不会恶化进水池前的进水流态。比较图8、图15和图16进水池前的流线可以看出,方案6进水池前的流线更均匀,入流方向更好。方案6和方案7各机组的站前行近流速分布较为均匀(图17),与方案0相比,各机组的进水流态改善较为明显。综合比较前池内流态和站前行近流速分布,方案6的方柱设置对前池内流态改善最佳。

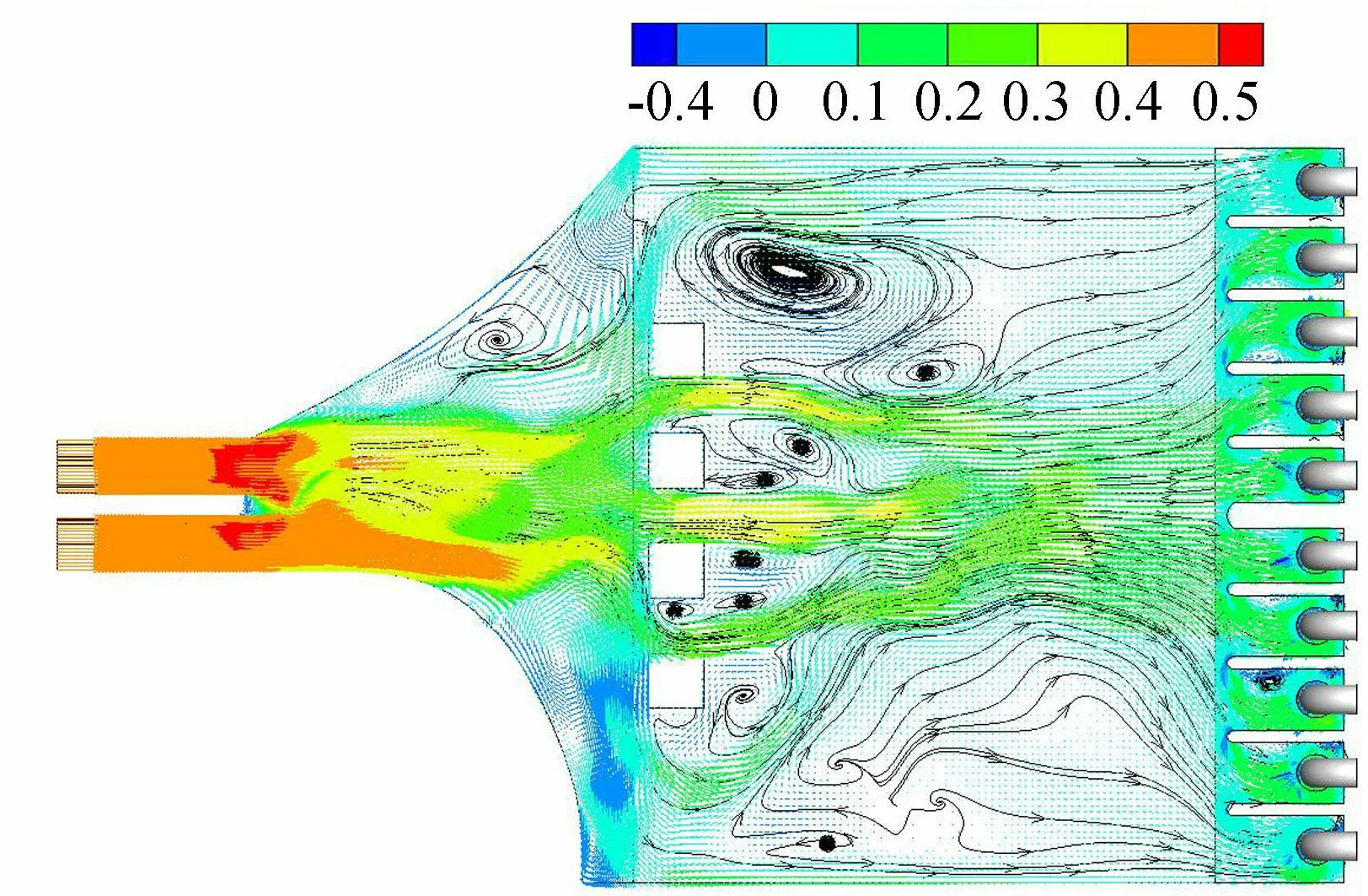
图15 方案6前池0.5H截面流速分布(单位：m/s)

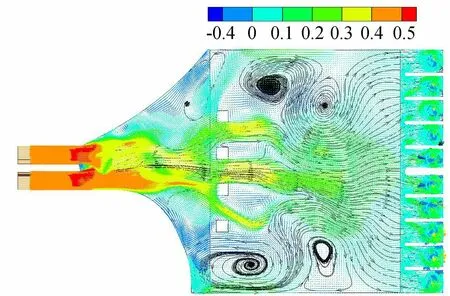
图16 方案7前池0.5H截面流速分布(单位：m/s)

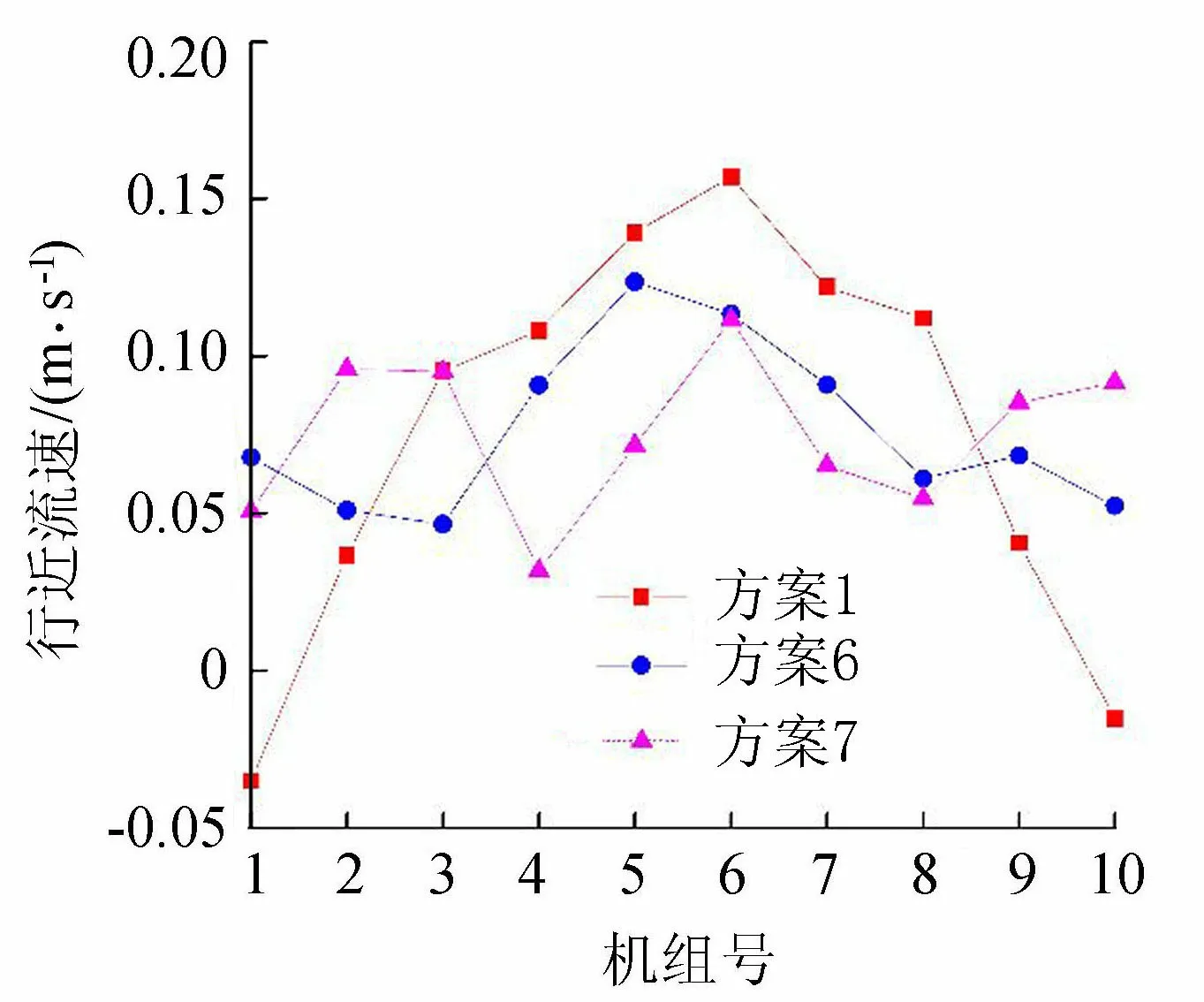
图17 不同方柱数量站前行近流速分布

改变方柱数量后计算前池的水力损失如表2所示。由表2可知,在前池内设置方柱和改变方柱的数量对水力损失的影响很小。随着方柱数量的减少(方案6、7),前池内水力损失增大,这是因为减小前池两侧方柱后,柱后的水流湍动加强。

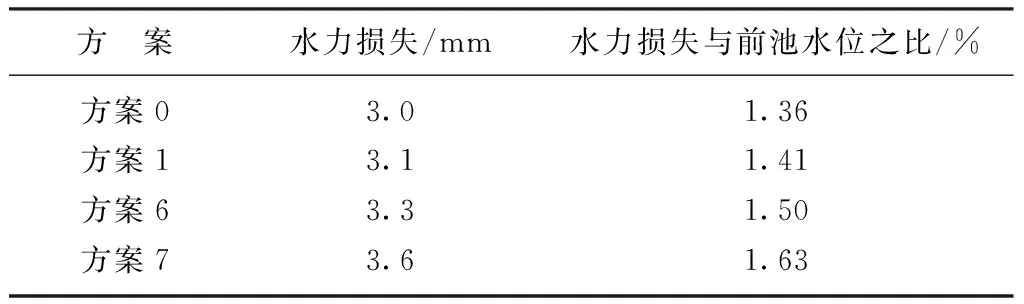
表2 前池内水力损失

图18为方案1在不同水位工况下站前行近流速分布。由图18可知,随着水位的增高,机组的站前行近流速变化变小,经过方柱调整后,进入进水池的水流变得更加均匀。水位过低时,站前行近流速分布变化较大,进入进水池的水流没有得到充分地调整。这说明,水位变化对前池内单排方柱整流效果影响较为明显。

图18 不同水位工况下方案1站前行近流速分布

4.5 单排方柱整流效果分析

综合分析上述各研究方案可知,当水流流经单排方柱时,由于单排方柱阻水分流作用,水流会流向前池两侧,改变前池两侧水流流态,减小两侧回流区。同时,在单排方柱后产生卡门漩涡,其范围受单排方柱位置、方柱宽度和数量的影响。水流受漩涡的影响,发生能量传递,行近流速由不均匀分布逐渐过渡到均匀分布(图19)。

图19 行近流速变化示意图

5 结 论

a. 无整流措施时,前池两侧水流存在大尺度回流区,泵站进水池前行近流速分布不均匀。

b. 单排方柱的位置布置方式对前池内流态改善有明显影响。当单排方柱位于0.6L0、宽度为0.05B0时,前池内流态得到很好改善,断面3行近流速分布合理。

c. 前池内水位变低会影响前池内单排方柱整流效果。

[ 1 ] 周济人,刘超,汤方平,等.泵站复杂前池内的流态改善研究[J].江苏农学院学报,1998(4):93-96.(ZHOU Jiren,LIU Chao,TANG Fangping,et al.Study on improving flow pattern of the complicated forebay of a pumping station[J].Jiangsu Agricultural Research,1998(4):93-96.(in Chinese))

[ 2 ] 罗缙,林颖.火(核)电站循环水泵房前池水力模型试验研究[J].河海大学学报(自然科学版),2000,28(5):106-110.(LUO Jin,LIN Ying.Hydraulic test of pump sumps of thermal (nuclear) power plant[J].Journal of Hohai University(Naturl Science),2000,28(5): 106-110.(in Chinese))

[ 3 ] 朱红耕.工程措施对水泵进水条件影响的试验研究[J].水力发电学报,2004,23(4):69-73.(ZHU Honggen.Experimental study on the influence of engineering measures upon the flow conditions of pump[J].Journal of Hydroelectric Engineering,2004,23(4):69-73.(in Chinese))

[ 4 ] 罗灿,刘超.多机组泵站侧向进水特性模拟和改进研究[J].水力发电学报,2015,34(1):207-214.(LUO Chan,LIU Chao.Numerical simulation and improvement of side-intake characteristics of multi-unit pumping station[J].Journal of Organic Chemistry,2015,34(1):207-214.(in Chinese))

[ 5 ] 刘超,成立,汤方平.取水前池复杂流动数值模拟[J].华北水利水电学院学报,2001(3):35-39.(LIU Chao,CHENG Li,TANG Fangli.Numerical simulation of three-dimensional turbulent flow for pumping forebay[J].Journal of North China Institute of Water Conservancy and Hydroelectric Power,2001(3):35-39.(in Chinese))

[ 6 ] 于永海,徐辉,程永光.泵站前池导流板整流措施数值模拟研究[J].水利水电技术,2006(9):41-43.(YU Yonghai.XU Hui.CHENG Yongguang.CFD Numerical simulation on modification of flow pattern with flow deflector atforebay of pumping station[J].Water Resources and Hydropower Engineering,2006(9):41-43.(in Chinese))

[ 7 ] 罗灿,成立,刘超.泵站正向进水前池底坎整流机理数值模拟[J].排灌机械工程学报,2014,32(5):393-398.(LUO Chan,CHENG Li,LIU Chao.Numerical simulation of mechanism for sill rectifyingflow in pumping station intake[J].Journal of Drainage and Irrigation Machinery Engineering,2014,32(5):393-398.(in Chinese))

[ 8 ] VERSTEEG H K,MALALASEKERA W.An introduction to computational fluid dynamics: the finite volume method[M].New York: Pearson Education,2007.

[ 9 ] 资丹,王福军,姚志峰,等.大型泵站进水流场组合式导流墩整流效果分析[J].农业工程学报,2015,31(16):71-77.(ZI Dan,WANG Fujun,YAO Zhifeng,et al.Effects analysis on rectifying intake flow field for large scale pumping station with combined diversion piers[J].Transactions of the Chinese Society of Agricultural Engineering,2015,31(16): 71-77.(in Chinese))

[10] 资丹,王福军,陶然,等.边界层网格尺度对泵站流场计算结果影响研究[J].水利学报,2016,47(2):139-149.(ZI Dan,WANG Fujun,TAO Ran,et al.Research for impacts of boundary layer grid scale on flow field simulation results in pumping station [J].Transactions of the Chinese Society of Agricultural Engineering,2016,47(2): 139-149.(in Chinese))

[11] 成立,刘超,周济人,等.泵站前池底坝整流数值模拟研究[J].河海大学学报(自然科学版),2001,29(3):42-45.CHENG Li,LIU Chao,ZHOU Jiren,et al.Numerical simulation of sill flows in the forebay of pumping station[J].Journal of Hohai University(Naturl Science),2001,29(3):42-45.(in Chinese))

[12] 刘梅清,林琦,梁兴,等.泵站前池流态改善效果的数值模拟分析[J].武汉大学学报(工学版),2012,45(2):152-156.(LIU Meiqing,LIN Qi,LIANG Xing,et al.Numerical simulation research on improving flow pattern of forebay of a pumping station[J].Engineering Journal of Wuhan University,2012,45(2):152-156.(in Chinese))

[13] 冯建刚,李杰.大型城市水源泵站前池流态及改善措施试验[J].水利水电科技进展,2010,30(2):70-74.(FENG Jiangang,LI Jie.Flow patterns in forebays of large urban water source pumping stations and countermeasures[J].Advances in Science & Technology of Water Resources,2010,30(2):70-74.(in Chinese))

[14] 冯旭松.泵站前池底坎整流及坎后流动分析[J].江苏水利,1998(1):31-33.(FENG Xusong.Flow rectification and analysis of sill in the forebay of pump station[J].Jiangsu Hydraulics,1998 (1):31-33.(in Chinese))

Numerical simulation of flow pattern in forebay of pump station with single row of square columns

XIA Chenzhi, CHENG Li, ZHAO Guofeng, YU Lei, WU Mutian, XU Wentao

(School of Hydraulic, Energy and Power Engineering, Yangzhou University, Yangzhou 225000, China)

In order to improve the flow pattern in the foreway of a pump station, the RNGk-εturbulence model based on the Fluent software was used to simulate the flow pattern in the front inflow forebay of a pump station with a single row of square columns, and the effect of geometric parameters of these square columns on the flow pattern in the foreway was analyzed. The results show that a single row of square columns leads to flow separation, the water flowing through the square columns disperses to the two sides of the foreway, and vortices form behind the square columns. Without rectification measures, the flow pattern is disorderly in the forebay, but it is significantly improved when a single row of square columns are arranged in the forebay. These square columns should be arranged in the forepart and middle of the forebay, not in the backflow zone at the two sides. The flow separation effect decreases and the approach velocity is more non-uniform with the decrease of the width of square columns.

pump station; forebay; rectification measure; square column; flow pattern; numerical simulation

国家科技支撑计划(2015BAD201301-02);江苏省研究生培养创新工程(KYLX16-1395);江苏省大学生学术科技创新基金(201611117030Z)

夏臣智(1990—)，男，博士研究生，主要从事泵站工程研究。E-mail:xiachenzhi@foxmail.com

成立(1975—)，男，教授，博士，主要从事泵站工程研究。E-mail:chengli@zu.edu.cn

10.3880/j.issn.1006-7647.2017.04.010

TV135;TV675

A

1006-7647(2017)04-0053-06

2017-01-08 编辑：郑孝宇)