基于荷载传递法的嵌岩锚杆抗拔承载特性
2017-07-05尹君凡陈秋南贺成斌
雷 勇,尹君凡,陈秋南,贺成斌
(湖南科技大学岩土工程稳定控制与健康监测湖南省重点实验室,湖南 湘潭 411201)
基于荷载传递法的嵌岩锚杆抗拔承载特性
雷 勇,尹君凡,陈秋南,贺成斌
(湖南科技大学岩土工程稳定控制与健康监测湖南省重点实验室,湖南 湘潭 411201)
为研究嵌岩锚杆抗拔过程中锚-岩界面承载特性,根据岩质地基中嵌岩锚杆的受力破坏机理,采用二段线性函数模拟锚杆-围岩界面的力学行为;基于荷载传递理论,推导了岩质地基中嵌岩锚杆的轴力、侧阻力及锚头位移的计算公式,分析了综合影响系数η对嵌岩锚杆抗拔承载特性的影响,给出了相应的确定方法;结合工程算例采用提出的计算方法对锚杆的轴力、侧阻力及P-S曲线进行了分析。分析结果表明:当上拔荷载较小时,嵌岩锚杆侧阻力呈双曲函数分布;当上拔荷载较大时出现塑性区,塑性区侧阻力均匀分布,弹性区呈双曲函数分布。
嵌岩锚杆;承载特性;荷载传递理论;综合影响系数
近年来,嵌岩锚杆广泛用于岩质地基中的建(构)筑物基础与边坡失稳防治工程中,以承受由水平荷载及弯矩作用引起的上拔荷载[1-3]。较多学者对嵌岩锚杆的承载特性展开了研究,如郑卫锋等[4]对输电线路岩石锚杆基础进行了试验研究,得到了其破坏形态及极限承载力值,并给出了相关设计计算参数的取值;孙益振等[5]进行了节理化岩体注浆锚杆基础抗拔模型试验,结果表明锚杆和岩体之间的黏结强度是控制试验结果的主要因素,并影响着锚杆的极限抗拔力和破坏状态;张琰等[6]在中风化砂岩地质条件下开展了岩质地基嵌岩锚杆的足尺试验研究,得到了荷载-位移曲线,分析了岩质地基嵌岩锚杆破坏模式和承载性能;何思明等[7]根据弹性理论,推导了锚杆在完全黏结条件下界面剪应力分布公式,并研究了界面脱黏段的剪应力分布及脱黏段长度。陈国周等[8]考虑锚固段界面摩阻力的非线性特征,采用软化模型对锚固段与土体之间的黏结力沿锚固段长度的分布情况进行了分析;朱训国等[9]推导了锚杆与注浆体或岩体耦合情况下的解析本构方程,并对其进行了参数分析;赵明华等[10]基于锚杆-岩石作用的剪胀机制,建立了桩底嵌岩锚杆的弹性状态下的荷载传递函数;张培胜等[11]结合锚杆抗拔模型试验实测数据,采用弹塑性软化本构模型拟合锚杆锚固段剪应力与位移之间关系。然而采用荷载传递理论分析弹塑性软化条件下岩质地基嵌岩锚杆的轴力、侧阻力及锚杆位移特性的报道并不多见。
有研究[12-13]表明:锚固段侧阻力并非均匀分布,而是在其前段形成峰值,逐步向末端减小并最终趋近于零。然而目前锚杆的设计方法假设锚固段侧阻力为定值,不考虑锚杆与周围岩土体之间的胶结特性随深度的改变而发生变化。这一假定显然与实际情况存在差异,因此开展预测锚固段的侧阻力及轴力的分布规律研究,对于正确认识岩质地基嵌岩锚杆作用机制,优化岩质地基嵌岩锚杆的设计等具有重要的理论意义和工程实用价值。
本文以二段线性软化模型为基础,采用荷载传递理论,推导了岩质地基嵌岩锚杆的轴力、侧阻力及锚头位移的计算公式,并对综合影响因素η的确定方法和对岩质地基嵌岩锚杆抗拔承载特性的影响进行了探讨。
1 嵌岩锚杆侧阻力计算模型
1.1 嵌岩锚杆的破坏模式及假定
一般而言,锚杆的极限抗拔承载力主要受4个方面的因素控制:杆体材料强度、杆体与砂浆间的握裹力、锚杆与岩土层间的侧阻力和地基的完整程度。相应地在岩质地基中,嵌岩锚杆存在4种破坏模式:锚筋拉断破坏、锚筋被拔出破坏、锚杆被拔出破坏和基岩整体剪切破坏。在保证锚头装置可靠、锚杆杆体有足够的截面积承受拉力及锚固岩体在最不利条件下仍能保持整体稳定性等前提条件下,锚杆抗拔承载力主要取决于锚固段周围岩层对锚杆的侧阻力。徐前卫等[14]开展的岩体锚杆抗拔力试验也表明,锚杆的失效主要是由灌浆体与岩土体之间的剪切破坏所致。因此本文假定锚杆被拔出破坏模式对岩质地基嵌岩锚杆抗拔承载特性进行分析。
1.2 嵌岩锚杆锚-岩界面剪切模型
嵌岩锚杆侧阻力本质是注浆材料(水泥、砂浆或细石混凝土)与孔壁岩体界面的摩擦力。当上拔荷载增大时,锚杆与围岩界面开始产生相对位移,由此产生侧阻力。随着界面相对位移的增大,锚-岩界面的剪切力呈线性增大,当界面相对位移达到界面极限相对位移sm时,锚-岩界面发生塑性破坏。界面的剪切过程伴随着软化现象,界面强度由峰值强度τm下降至残余剪切强度τr。锚-岩界面塑性破坏的微观机理可由剪胀机理解释,其破坏过程如图1所示。
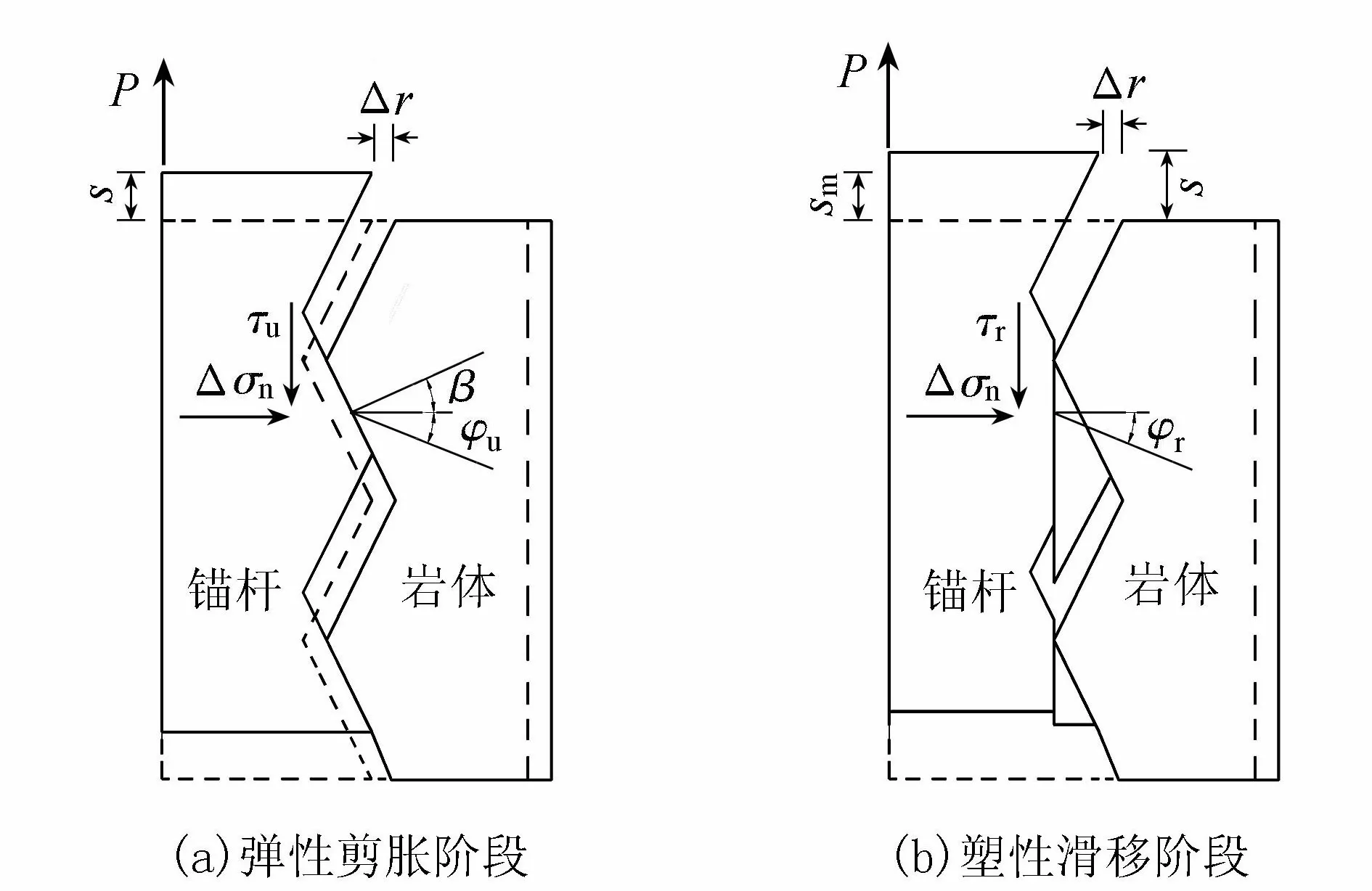
图1 锚-岩界面破坏过程
1.2.1 弹性剪胀阶段
当嵌岩锚杆与周围岩体发生相对位移时,其受力机制初始为滑动剪胀机制,如图1(a)所示。在弹性剪胀阶段,锚-岩界面的法向应力增量Δσn可根据厚壁圆筒的弹性理论解[15]求得
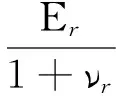
(1)
式中:Er为岩体的弹性模量;r为锚杆半径;Δr为岩壁的径向膨胀量;νr为岩石的泊松比;k为围岩的法向刚度。
根据图1(a)所示的几何关系,岩壁的径向膨胀量Δr为
Δr=stanβ
(2)
式中:s为锚-岩界面相对位移;β为剪胀角。
由式(1)(2),可得锚杆与围岩界面的法向应力增量为
Δσn=kstanβ(s≤sm)
(3)
式中sm为锚-岩界面极限相对位移,可由经验或室内结构面试验确定。
佩顿(Patton)在研究规则粗糙起伏岩石结构面抗剪强度时提出在法向应力较低时岩石结构面的抗剪强度τu表达式为
τu=Δσntan(φu+β)
(4)
式中φu为砂浆-岩石界面摩擦角。
依据结构面强度理论,将式(3)代入式(4)则一定深度z处锚-岩界面的侧阻力模型为
τ(z)=Ks(z)
(5)
其中K=ktanβtan(φu+β)
(6)
式中:K为界面剪切刚度系数,实际上反映了与岩壁剪胀角、材料性质、围岩模量对界面剪切性质的影响,可按文献[11]的建议综合取值;s(z)为深度z处的锚-岩界面相对位移。
1.2.2 塑性滑移阶段
当弹性剪胀阶段的界面相对位移达到界面极限相对位移sm时,锚-岩界面强度达到峰值强度τm,孔壁粗糙体随即发生破坏,破坏发生在抗剪强度较小的一侧,锚-岩界面进入塑性滑移阶段,如图1(b)所示,此时锚-岩界面强度由峰值强度τm下降至残余剪切强度τr,砂浆-岩石界面摩擦角由φu变为残余内摩擦角φr。
根据锚杆锚-岩界面剪胀滑移破坏机理可知,锚-岩界面的相对位移与剪切应力的关系可采用二段线性函数[16]描述,如图2所示, 数学表达式为
(7)
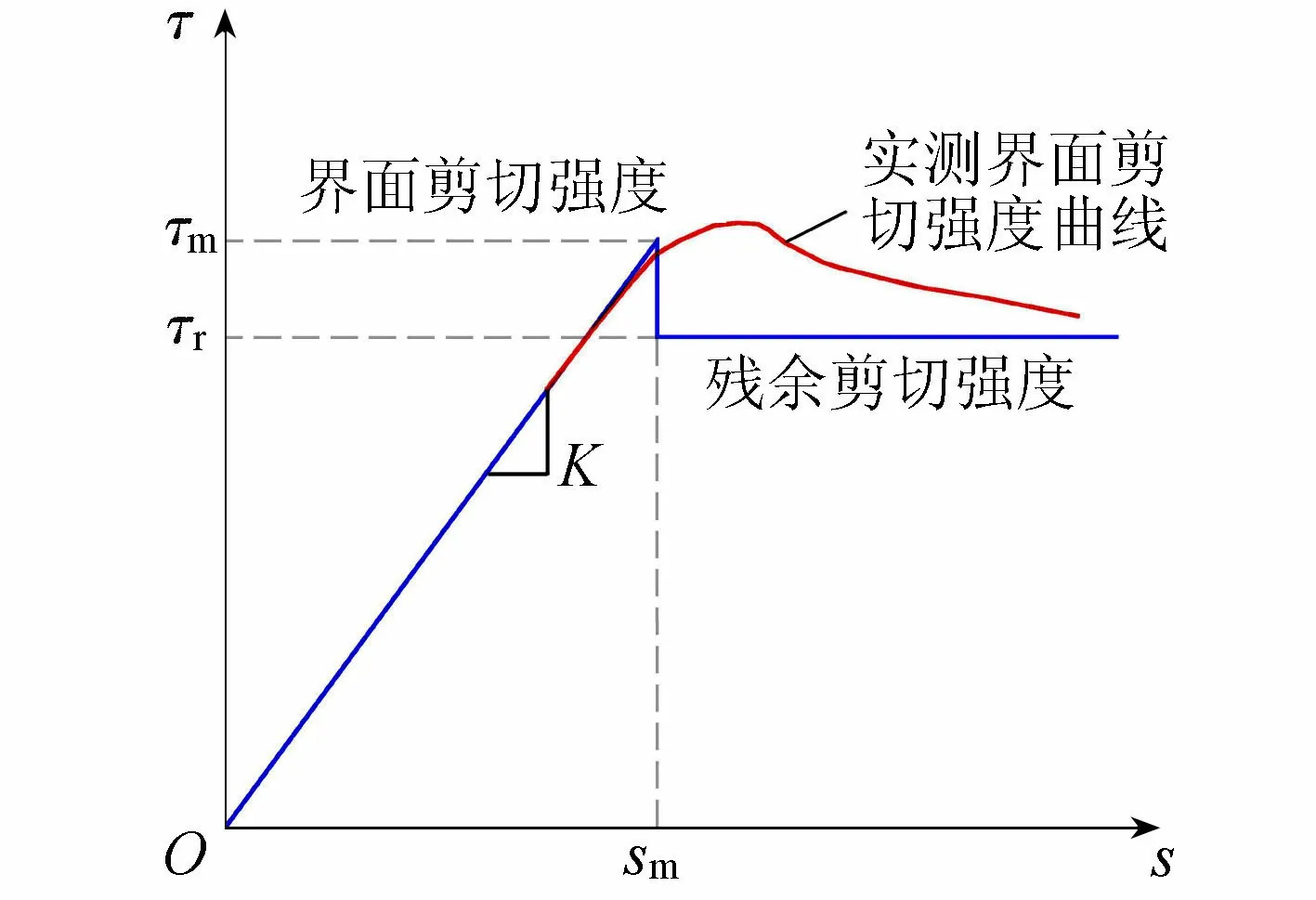
图2 锚-岩界面侧阻力
2 嵌岩锚杆位移、侧阻力及轴力计算
在嵌岩锚杆上拔过程中,锚-岩界面的侧阻力由上至下逐步发挥,荷载较小时界面侧阻力处于弹性阶段,此时锚头处锚-岩界面相对位移s(0)≤sm,如图3(a)所示;当荷载继续增大,如锚头处锚-岩界面相对位移s(0)>sm时,锚杆上部出现塑性区,侧阻力由峰值强度下降至残余强度,此时塑性区发展深度为l0,l0以下仍为弹性区,如图3(b)所示。
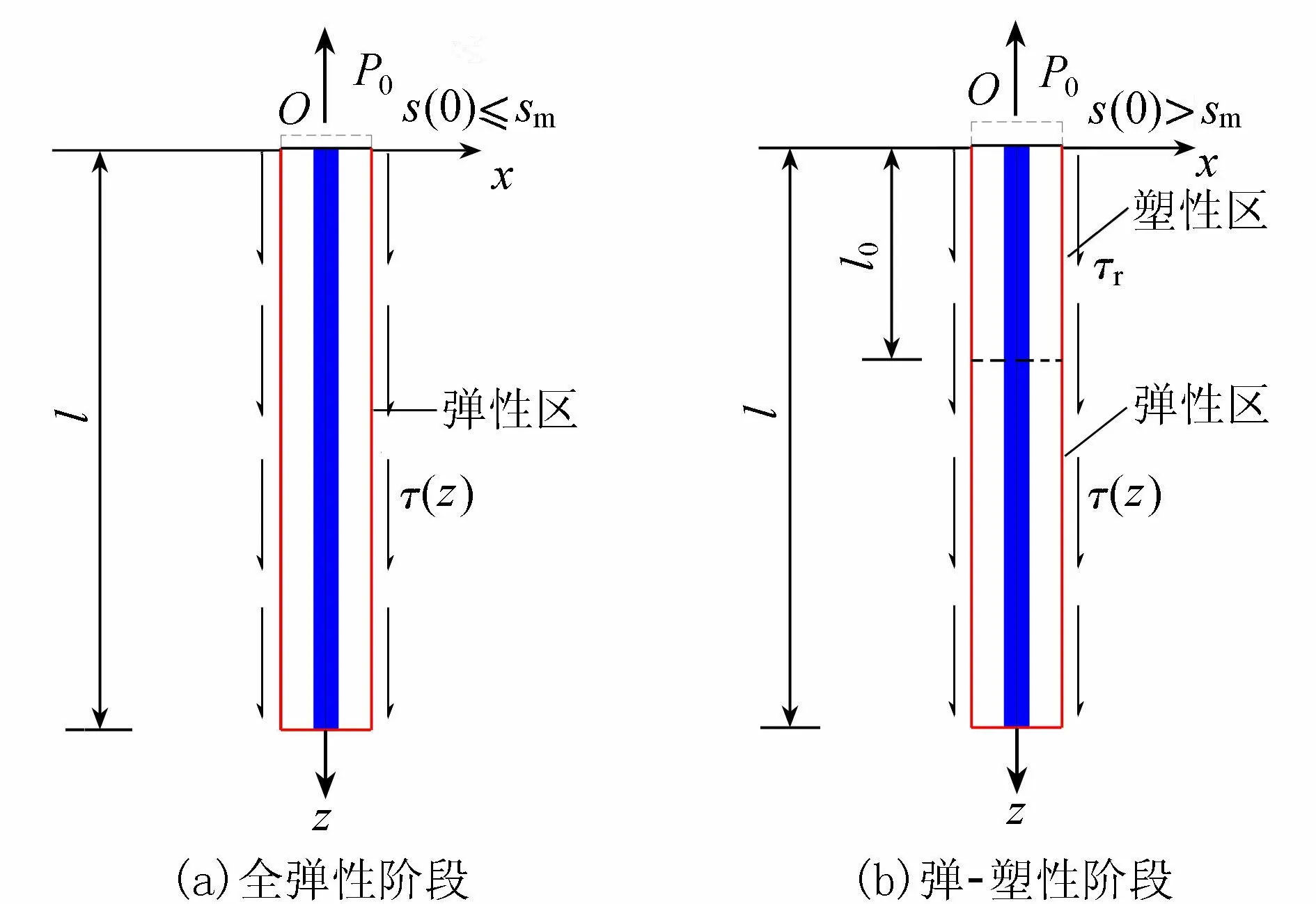
图3 嵌岩锚杆计算模型
2.1 弹-塑性阶段
2.1.1 塑性区(0≤z≤l0)
塑性区l0段(0≤z≤l0)内,侧阻力为常量τr。塑性区段在上拔荷载P0、锚杆轴力P1及侧阻力τr作用下处于静力平衡状态,按材料力学拉压杆件的变形量计算方法,由图4的计算模型可得到塑性区变形量计算公式为
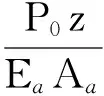
(8)
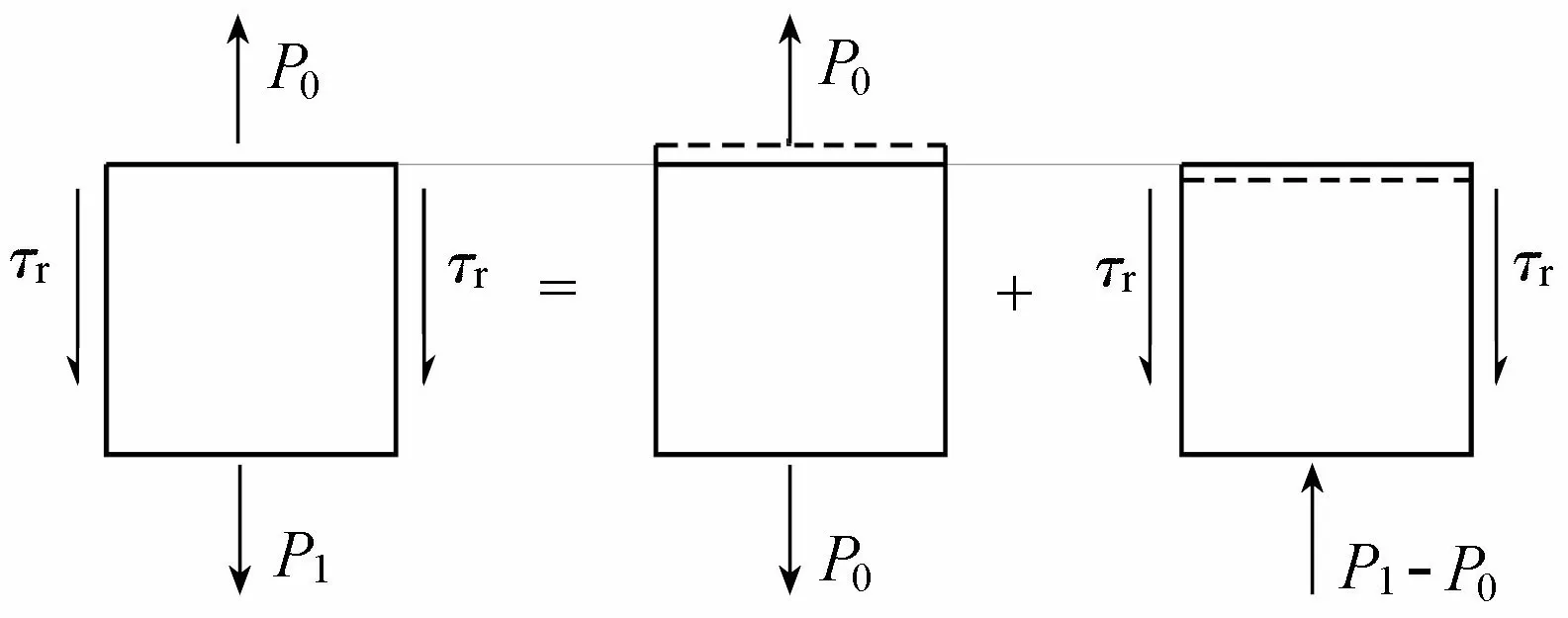
图4 塑性区变形量计算模型
式中:u为锚杆的周长;Aa为锚杆截面积;Ea为锚杆的弹性模量,且有Ea=(EgAg+EbAb)/(Ag+Ab),其中Eg、Eb分别为浆体与锚筋弹性模量,Ag、Ab分别为浆体与锚筋的截面积。
按轴力与变形的关系,可得塑性区轴力计算公式为
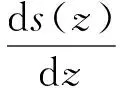
(9)
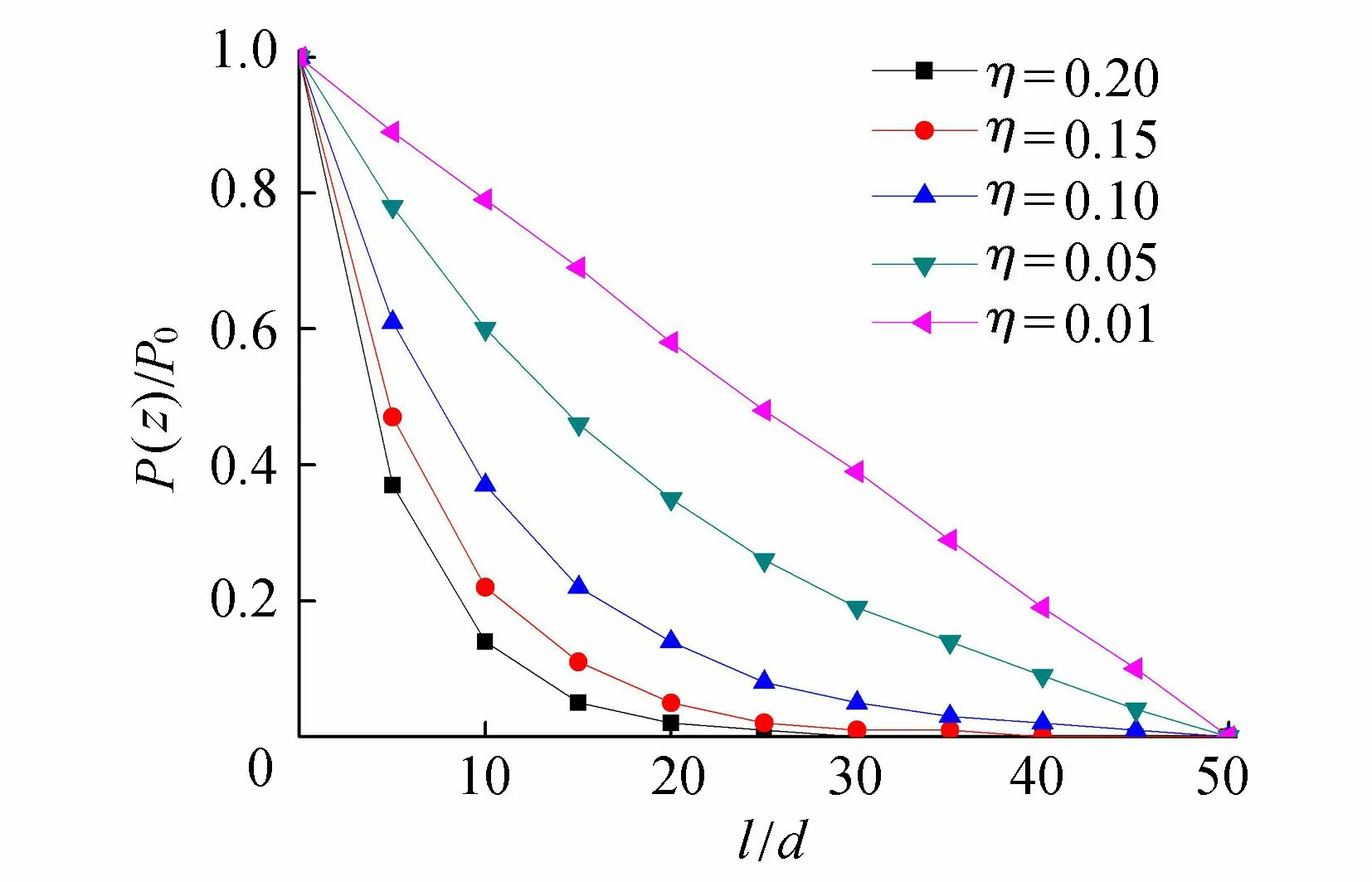
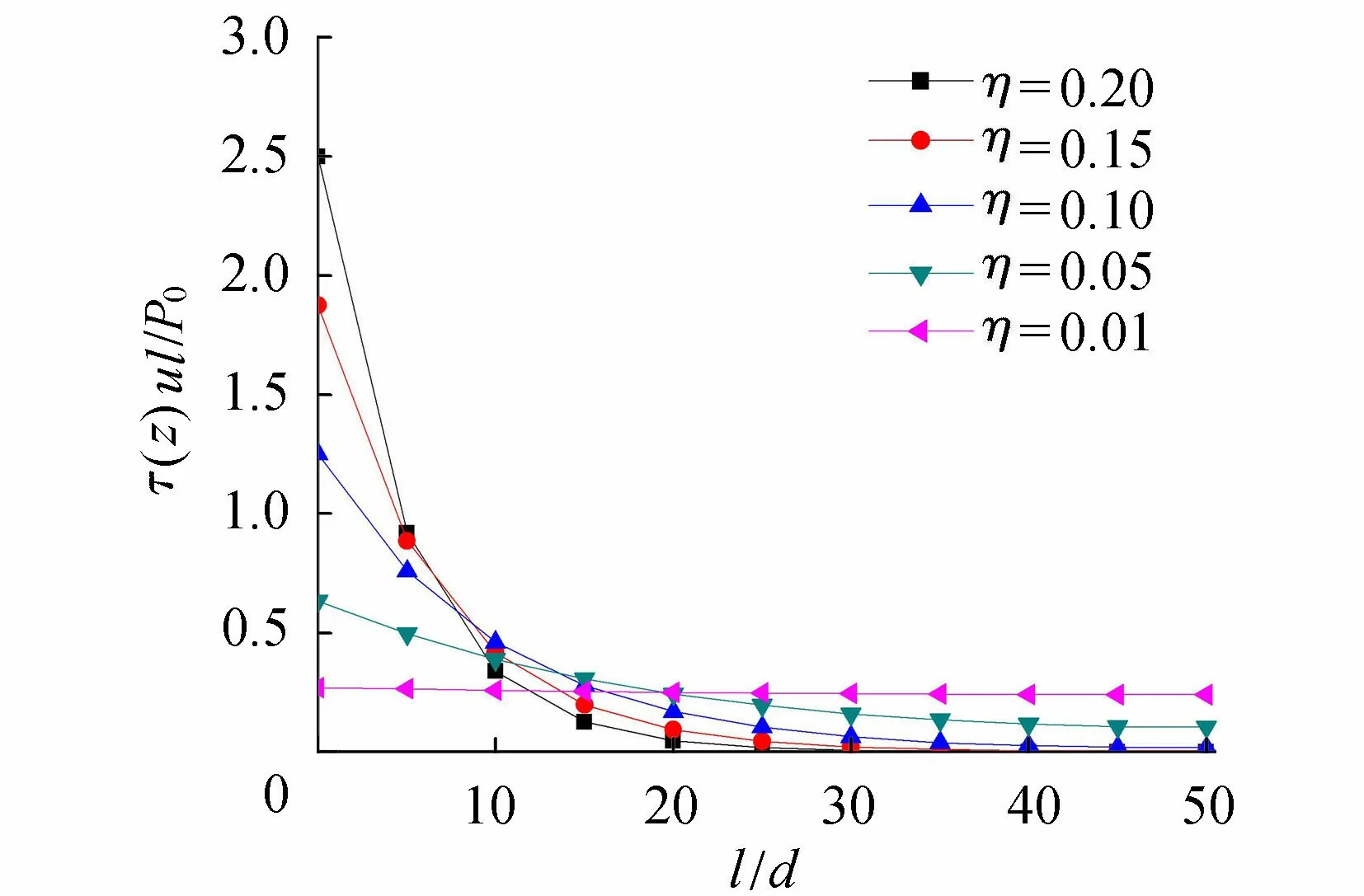
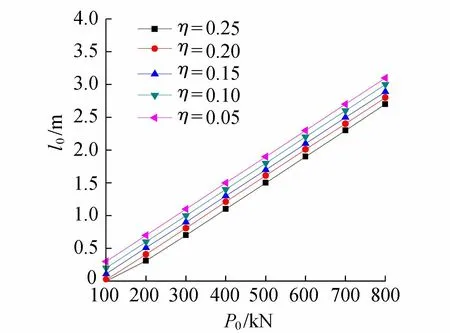
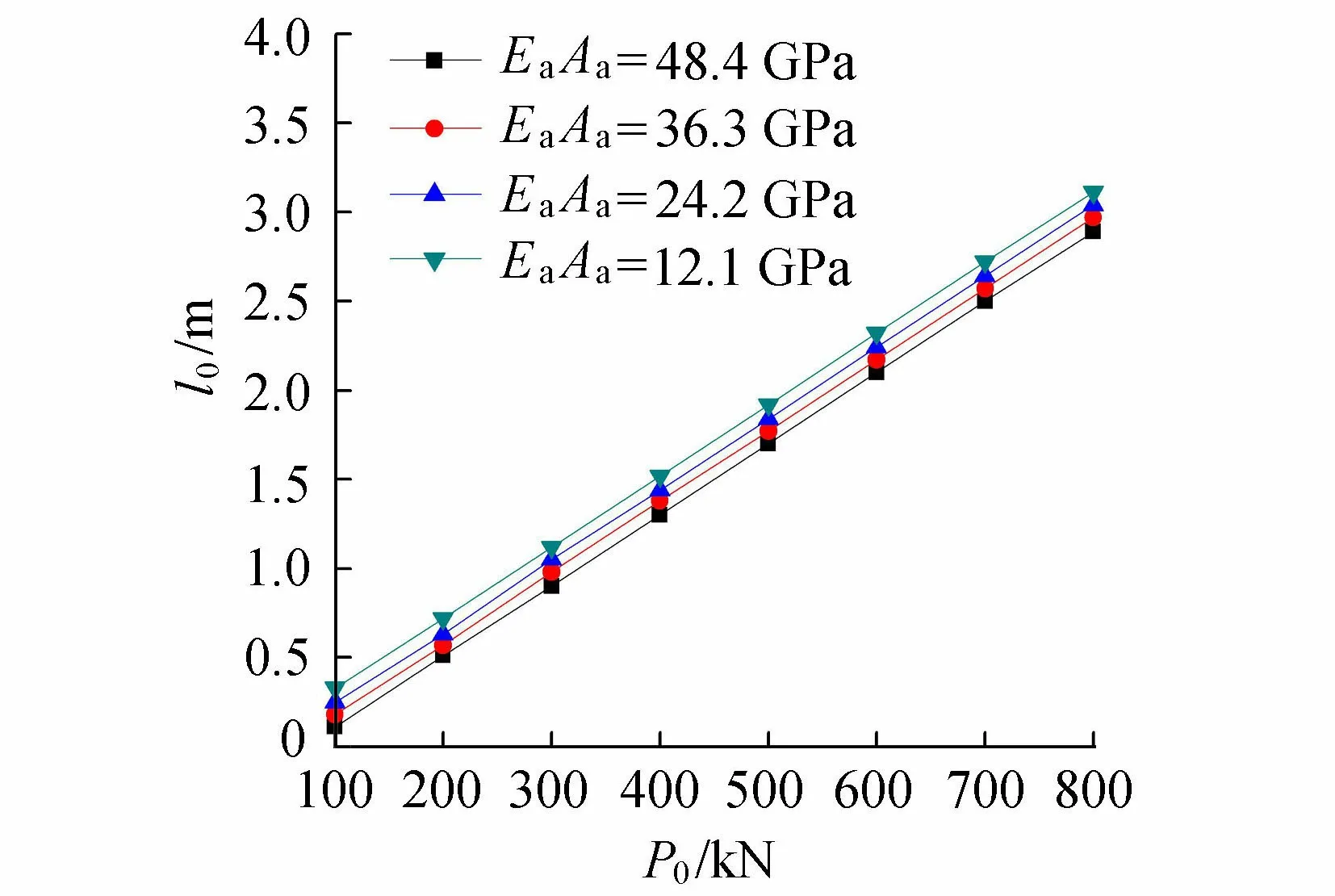
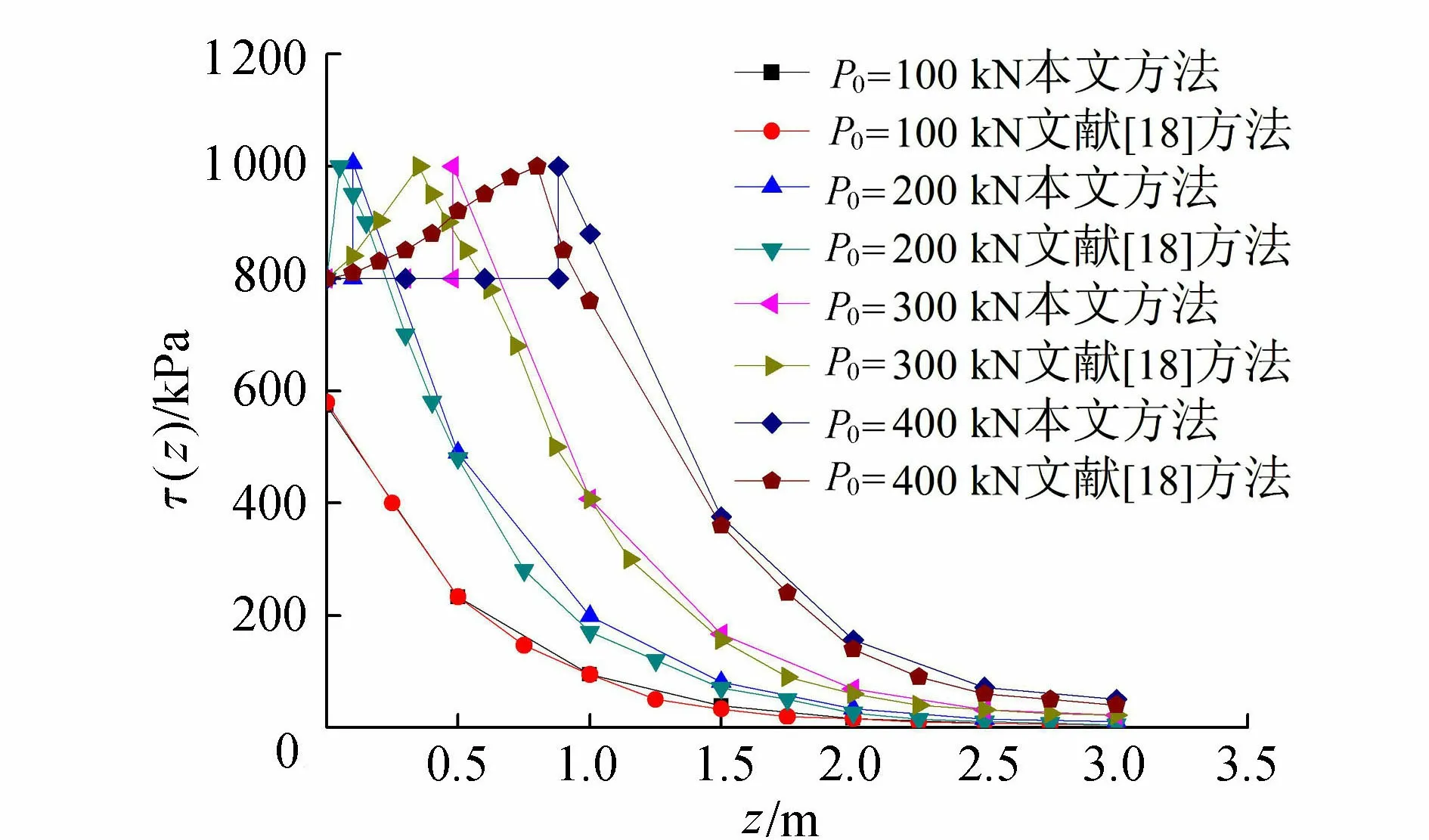
2.1.2 弹性区(l0 塑性区l0段以下(l0 (10) 将τ(z)=Ks(z)代入式(10)可得弹性区变形量计算公式为 (11) (12) 式中:c1、c2为待定系数;d为锚杆直径;η为综合影响系数,是反映岩壁剪胀角、锚-岩模量和锚径有关的综合影响参数,与嵌岩深度无关。 由塑性区和弹性区的2个轴力连续条件: (13) 可由式(11)解得弹性区(l0 (14) 进而解得弹性区轴力P(z)及侧阻力τ(z)的表达式为 (15) (16) 在弹-塑性区边界上,z=l0,且满足s2(l0)=sm及P(l0)=P0-τrul0,将两者代入式(14)整理可得 (17) 通过式(17)可解得塑性区长度l0。式(17)为关于l0的超越方程,可采用数值方法求解,具体求解方法见第3.3节。 此时锚头的总位移为两段变形量之和: (18) 2.2 弹性阶段 当上拔荷载较小,围岩均处于弹性状态时。此时只需令公式(15)(16)及(18)中的l0=0、P(l0)=P0,即可解得弹性状态时轴力P(z)、侧阻力τ(z)及锚头总位移S。 3.1 综合影响系数对嵌岩锚杆的承载特性影响 上述推导表明综合影响系数η对嵌岩锚杆的承载特性有较大影响。综合影响系数η是嵌岩锚杆与周围岩土体相互作用的一个综合宏观反映,并强烈地影响着锚杆的轴力及侧阻力随深度的分布。为简化分析,在此对锚-岩界面处于弹性状态下的受力进行分析。对式(15)(16)令l0=0,得到弹性阶段轴力及侧阻力归一化公式如下: (19) (20) 图5 轴力归一化曲线 图5为锚杆直径d=100 mm、长度l=5 m、不同η时,由式(19)计算的轴力比随深度的变化曲线,可以看出,η越大,轴力在锚杆顶端衰减越快,传递至锚杆下部的荷载就越小。当η较大时,一定深度处轴力为零,也即锚杆的临界长度,这也与以往的试验资料是吻合的。反之,η越小,轴力沿嵌固段衰减越缓,分布也趋于均匀。 图6为由式(20)计算的同条件下侧阻力归一化曲线,其特点是η越大,嵌岩锚杆侧阻力在锚杆顶端分布就越集中, 递减速率越大,荷载传递深度有限。在一定的深度处,侧阻力基本为零。η越小,侧阻力分布也越趋于均匀,且锚杆全长范围内均受荷载。因此η是体现嵌岩锚杆承载性能的宏观综合指标。按式(12)的定义,在一定锚杆直径下,η实际上反映了剪切刚度与锚杆弹性模量比值的大小。当锚杆的设计长度较小时,应选用较大的锚-岩界面综合影响系数η。 图6 侧阻力归一化曲线 3.2 综合影响系数的确定方法 当无现场实测资料时,综合影响系数η可按式(12)估算,所需的参数为锚杆直径d、界面剪切刚度系数K及锚杆的弹性模量,其中K可按室内混凝土-岩石界面的剪切试验确定或参考文献[11]按下式确定: (21) 式中νa为注浆材料的泊松比。 当有实测资料时,η可通过现场嵌岩锚杆抗拔试验的P-S曲线线性变形段的数据按下式求得: (22) 式中:Pd为线性变形段上拔荷载;sd为线性变形段位移量。 如有轴力曲线或侧阻力随深度变化的曲线,也可按式(15)及(16)对比分析得到。 3.3 塑性区长度影响因素 由式(17)可见,锚杆上拔荷载P0、残余剪切强度τr、锚杆抗拉刚度EaAa、锚杆直径d及综合影响系数η均会对塑性区长度l0的计算结果产生影响。下面采用算例对P0、EaAa及η这几个主要参数进行分析,取锚杆直径为100 mm、长度为5 m,材料参数的取值参照第4节的工程算例。由于式(17)为超越方程,l0的计算可采用迭代法,具体步骤如下: a. 令: F1(l0)=P0-τrul0 (23) (24) b. 给定初值P0、EaAa、τr、d、η及sm。 c. 将l0j=l0(j为迭代次数,初值j=1)代入式(23)及(24),计算F1(l0j)及F2(l0j)。 e. 输出塑性区深度l0。 f. 返回步骤b改变初始条件,得到不同参数下的l0。 图7和图8为采用上述计算方法得到的塑性区深度l0的变化规律。图7为EaAa=48.4 GPa、不同η条件下l0随上拔荷载的变化规律。由图7可知l0随上拔荷载的增大基本呈线性增长,在低荷载(<100 kN)下基本不出现塑性区,荷载每增大100 kN,塑性区增长约0.4 m。在相同荷载下,η每减小0.05,塑性区增长约0.1 m,相关性较好。 图7 不同η条件下l0的变化规律 图8 不同EaAa条件下l0的变化规律 图8为η=0.15、不同EaAa条件下l0随上拔荷载的变化规律。由图8可知l0随上拔荷载的增大同样呈线性增长,荷载每增大100 kN,塑性区增长约0.4 m。在相同荷载下,EaAa每减小12.1 GPa,塑性区增长约7 cm。 为验证本文方法的合理性,结合文献[6]进行岩质地基嵌岩锚杆的抗拔承载特性分析。文献[6]针对中风化砂岩地基开展了嵌岩锚杆现场抗拔试验研究。试验场地位于某风电场内,场地附近地表覆盖层为粉细砂层,其下为厚层砂岩。岩石单轴饱和抗压强度Rc=46.8 MPa,通过岩石弹性波速测试,得到岩石完整性指数Kv=0.17,岩体完整程度为破碎。锚杆孔径为 100 mm,嵌岩锚杆的长度为3.0 m,锚筋材质为HRB400 螺纹钢,锚筋直径为 36 mm,锚孔内均灌注C30 细石混凝土,加入适量膨胀剂。其他相应的力学及材料参数[17]为:τm=1.0 MPa,τr=0.8 MPa,sm=1.0 mm,K=1.44 MPa/mm,Eg=25 GPa,Eb=210 GPa。 图9 侧阻力沿深度分布 根据实测的P-S曲线的线性段斜率,采用式(22)求得综合影响系数η=0.38。为分析各级荷载下锚杆的侧阻力分布,采用本文方法与文献[18]所提供的考虑锚-岩界面软化特征的非线性计算方法进行了对比分析,且两种方法假定的峰值强度、极限位移及残余强度一致。由图9可见,随着上拔荷载的增大,塑性区逐渐由上部展开,不断下移。塑性区内侧阻力为常量,塑性区以下锚杆侧阻力沿深度呈非线性分布。本文方法计算结果显示,100 kN时锚杆处于弹性状态,200 kN时的塑性区深度为10 cm,300 kN时的塑性区深度为48 cm,400 kN时的塑性区深度为88 cm。采用文献[18]方法计算结果为:100 kN时锚杆处于弹性状态,200 kN时的塑性区深度为5 cm,300 kN时的塑性区深度为35 cm,400 kN时的塑性区深度为81 cm。由于二段线性函数与实际的软化关系在线性段是吻合的,因此在全弹性条件下,两种方法计算的侧阻力曲线重合。在峰值强度后,实际的软化曲线渐变至残余剪切强度,而二段线性函数则直接跌落至残余剪切强度,采用二段线性函数计算的塑性区深度较考虑软化特征的非线性计算方法计算结果偏大,是由于后者的平均残余摩擦力较前者的大,在相同的上拔荷载下,后者在塑性区分担了更多的荷载,同时导致弹性区各点的侧阻力较前者小,但总的变化趋势基本一致。 各级上拔荷载下的轴力如图10所示。由图10可见在荷载较低时,锚杆轴力沿深度z呈非线性曲线变化,未出现塑性区,当荷载达到约160 kN时出现塑性区,塑性区由于侧阻力为常数,锚杆轴力沿深度线性减小。实测与计算各级荷载下的锚头位移量如11所示。由图11可见,锚头位移在全弹性阶段与荷载呈线性变化关系,在局部塑性阶段,由于塑性位移的增加,荷载曲线在该阶段呈非线性变化。由图10和图11可知,轴力和锚头位移理论计算值与实测值较为接近。 图10 轴力实测与计算结果对比 图11 锚头实测与计算P-S曲线 a. 当上拔荷载较小时,嵌岩锚杆侧阻力呈双曲函数分布;当上拔荷载较大时,出现塑性区,塑性区侧阻力均匀分布,弹性区呈双曲函数分布。二段线性模型能较好地模拟锚-岩界面的力学特性。 b. 综合影响系数η越大,轴力在锚杆顶端衰减越快,传递至锚杆下部的荷载就越小。当η较大时,一定深度处轴力为零。反之,η越小,轴力沿嵌固段衰减越缓,分布也趋于均匀。 c. 综合影响系数η越大,嵌岩锚杆侧阻力在锚杆顶端分布就越集中,递减速率越大,荷载传递深度有限。η越小,侧阻力分布也越趋于均匀,且锚杆全长范围内均受荷载作用。 d. 综合影响系数η可通现场嵌岩锚杆抗拔试验P-S曲线线性变形段的斜率求得。 [ 1 ] 任少龙,徐磊.自钻式锚杆在溪洛渡水电站左岸竖井施工中的应用[J].水利水电科技进展,2010,30(1):52-55.(REN Shaolong,XU Lei.Application of self-driving anchor bolts in vertical shaft at left bank of Xiluodu Hydropower Station[J].Advances in Science and Technology of Water Resources,2010,30(1):52-55.(in Chinese)) [ 2 ] 张德圣,姜玉松,吴诗勇.小湾水电站堆积体边坡支护与锚索技术应用[J].水利水电科技进展,2011,31(2):66-70.(ZHANG Desheng,JIANG Yusong,WU Shiyong.Reinforcing of deposit slopes of Xiaowan Hydropower Station and application of prestressed anchorage cables[J].Advances in Science and Technology of Water Resources,2011,31(2):66-70.(in Chinese)) [ 3 ] 李宏恩,李铮,范光亚,等.龙江水电站坝后厂房高边坡锚杆应力分析[J].水利水电科技进展,2012,32(4):59-62.(LI Hongen,LI Zheng,FANG Guangya,et al.Analysis of anchor bar stress for high slopes of powerhouse at dam toe of Longjiang Hydropower Plant[J].Advances in Science and Technology of Water Resources,2012,32(4):59-62.(in Chinese)) [ 4 ] 郑卫锋,邓海骥,何金业.输电线路岩石锚杆基础试验研究[J].建筑科学,2012,28(9):57-59.(ZHENG Weifeng,DENG Haiji,HE Jinye.Experiment research of rock anchor foundation in transmission line[J].Building Science,2012,28(9):57-59.(in Chinese)) [ 5 ] 孙益振,郑卫锋,范志强.输电线路节理化岩体注浆锚杆基础抗拔力模型试验研究[J].岩土力学,2012,33(1):78-82.(SUN Yizhen,ZHENG Weifeng,FAN Zhiqiang.Tension model test research on grouted bolts foundation in jointed rock masses for transmission line[J].Rock and Soil Mechanics,2012,33(1):78-82.(in Chinese)) [ 6 ] 张琰,郑卫锋,朱照清.用于砂岩加固的锚杆的承载性能试验研究[J].岩土力学,2015,36(增刊1):367-371.(ZHANG Yan,ZHENG Weifeng,ZHU Zhaoqing.Test research on bearing capacity of anchors used for sandstone reinforcement[J].Rock and Soil Mechanics,2015 36(Sup1):367-371.(in Chinese)) [ 7 ] 何思明,田金昌,周建庭.胶结式预应力锚索锚固段荷载传递特性研究[J].岩石力学与工程学报,2006,25(1):117-121.(HE Siming,TIAN Jinchang,ZHOU Jianting.Study on load transfer of bond prestressed anchor rope[J].Chinese Journal of Rock Mechanics and Engineering,2006,25(1):117-121.(in Chinese)) [ 8 ] 陈国周,贾金青.拉力型锚杆应力分布的非线性分析[J].地下空间与工程学报,2008,4(1):45-50.(CHEN Guozhou,JIA Jinqing.Nonlinear analysis of stress distribution of tension anchor[J].Chinese Journal of Underground Space and Engineering,2008,4 (1):45-50.(in Chinese)) [ 9 ] 朱训国,杨庆,栾茂田.岩体锚固效应及锚杆的解析本构模型研究[J].岩土力学,2007,28(3):527-532.(ZHU Xunguo,YANG Qing,LUAN Maotian.Study of reinforcement effect of anchored rock masses and analytic constitutive equation for rock bolt [J].Rock and Soil Mechanics,2007,28(3):527-532.(in Chinese)) [10] 赵明华,龙照,邹新军.基于剪胀效应的桩底嵌岩锚杆荷载传递分析法[J].岩土力学,2008,29(7):1938-1942.(ZHAO Minghua,LONG Zhao,ZOU Xinjun.Load transfer method of rock-socketed anchoring rods under pile tip considering dilatancy effect[J].Rock and Soil Mechanics,2008,29(7):1938-1942.(in Chinese)) [11] 张培胜,阴可.拉力型锚杆锚固段传力机理的全过程分析方法[J].地下空间与工程学报,2009,5(4):716-723.(ZHANG Peisheng,YIN Ke.An analysis method of the whole working course for the force transferring mechanism in fixed segment of tensile-type anchor bar[J].Chinese Journal of Underground Space and Engineering,2009,5(4):716-723.(in Chinese)) [12] 张季如,唐保付.锚杆荷载传递机理分析的双曲函数模型[J].岩土工程学报,2002,24(2):188-192.(ZHANG Jiru,TANG Baofu.Hyperbolic function model to analyze load transfer mechanism on bolts[J].Chinese Journal of Geotechnical Engineering,2002,24(2):188-192.(in Chinese)) [13] 尤春安.预应力锚索锚固段界面滑移的细观力学分析[J].岩石力学与工程学报,2009,28(10):1976-1985.(YOU Chunan.Analysis of interfacial slip mesomechanics in anchorage section of prestressed anchor cable[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(10):1976-1985.(in Chinese)) [14] 徐前卫,朱合华,金方方,等.软弱破碎岩体中锚杆抗拔受力机理及试验研究[J].地下空间与工程学报,2011,7(5):830-835.(XU Qianwei,ZHU Hehua,JIN Fangfang,et al.Study on the pullout mechanism of anchor bolt in weak and fractured rock mass and its model test[J].Chinese Journal of Underground Space and Engineering,2011,7(5):830-835.(in Chinese)) [15] JONSTON I W,LAM T S K,WILLIAMS A F.Constant normal stiffness direct shear testing for socketed pile design in weak rock[J].Geotechnique,1987,37 (1):83-89. [16] CAI Y,ESAKI T,JIANG Y J.An analytical model to predict axial load in grouted rock bolt for soft rock tunneling[J].Tunnelling and Underground Space Technology,2004,19:607-618. [17] 韩军,陈强,刘元坤,等.锚杆灌浆体与岩(土)体间的粘结强度[J].岩石力学与工程学报,2005,24(19):3482-3486.(HAN Jun,CHEN Qiang,LIU Yuankun,et al.Bond strength between anchor grout and rock or soil masses[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(19):3482-3486.(in Chinese)) [18] 黄明华,周智,欧进萍.拉力型锚杆锚固段拉拔受力的非线性全历程分析[J].岩石力学与工程学报,2014,33(11):2190-2199.(HUANG Minghua,ZHOU Zhi,OU Jinping.Nonlinear full-range analysis of load transfer in fixed segment of tensile anchors[J].Chinese Journal of Rock Mechanics and Engineering,2014,33(11):2190-2199.(in Chinese)) Anti-pullout bearing characteristics of rock-socketed anchor based on load transfer method LEI Yong, YIN Junfan, CHEN Qiunan, HE Chengbin (Hunan Provincial Key Laboratory of Geotechnical Engineering for Stability Control and Health Monitoring, Hunan University of Science and Technology, Xiangtan 411201, China) In order to study the bearing characteristics of the interface between the anchor and rock in the anti-pullout process of a rock-socketed anchor, according to the failure mechanisms of the rock-socketed anchor in the rock foundation, the mechanical behavior of the interface between the anchor and surrounding rock was simulated using a two-segment linear function. The formulas of axial force, side resistance, and top vertical displacement of the rock-socketed anchor were derived based on the load transfer theory. The influence of the comprehensive influence coefficientηon the anti-pullout bearing characteristics of the rock-socketed anchor was analyzed, and the method for determining the value ofηwas provided. The axial force, side resistance, andP-Scurve for an engineering example were analyzed using the presented calculation method. Results show that, when the uplift load is small, the side resistance of the rock-socketed anchor shows a hyperbolic distribution. When the uplift load is larger, the plastic zone appeares. The side resistance shows a uniform distribution in the plastic zone and a hyperbolic distribution in the elastic zone. rock-socketed anchor; bearing characteristic; load transfer theory; comprehensive influence coefficient 国家自然科学基金(51208195, 41372303);岩土工程稳定控制与健康监测湖南省重点实验室开放基金(E21618) 雷勇(1983—),男,讲师,博士,主要从事桩基础设计及工程应用研究。E-mail:leiyonghnu@163.com. 10.3880/j.issn.1006-7647.2017.04.013 TU473.1+1 A 1006-7647(2017)04-0070-07 2016-07-06 编辑:熊水斌)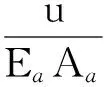
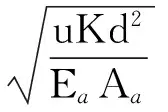
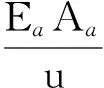
3 关键参数影响分析及确定方法
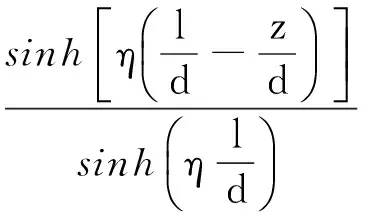
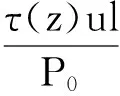
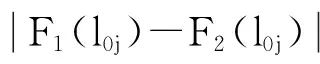
4 工程算例
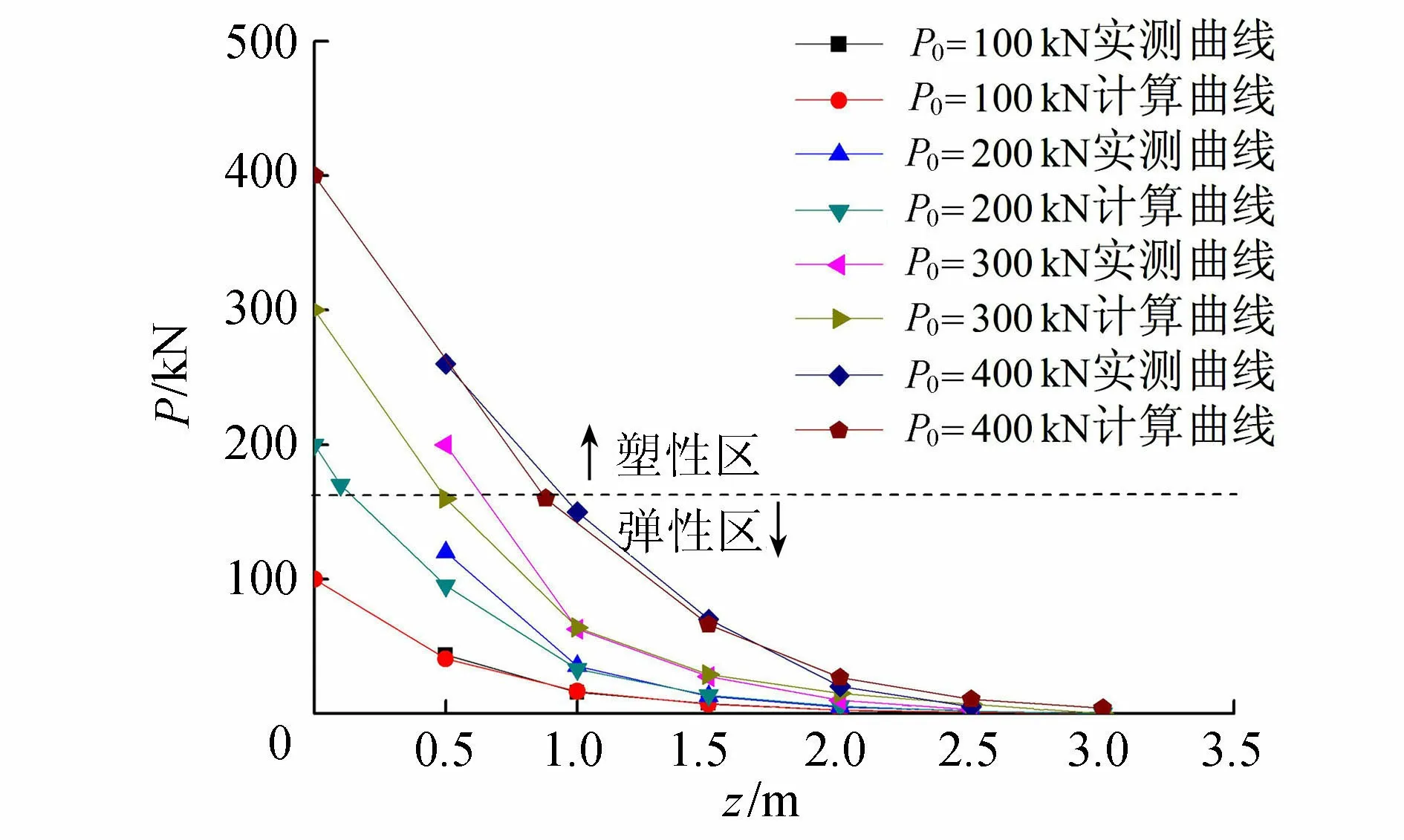
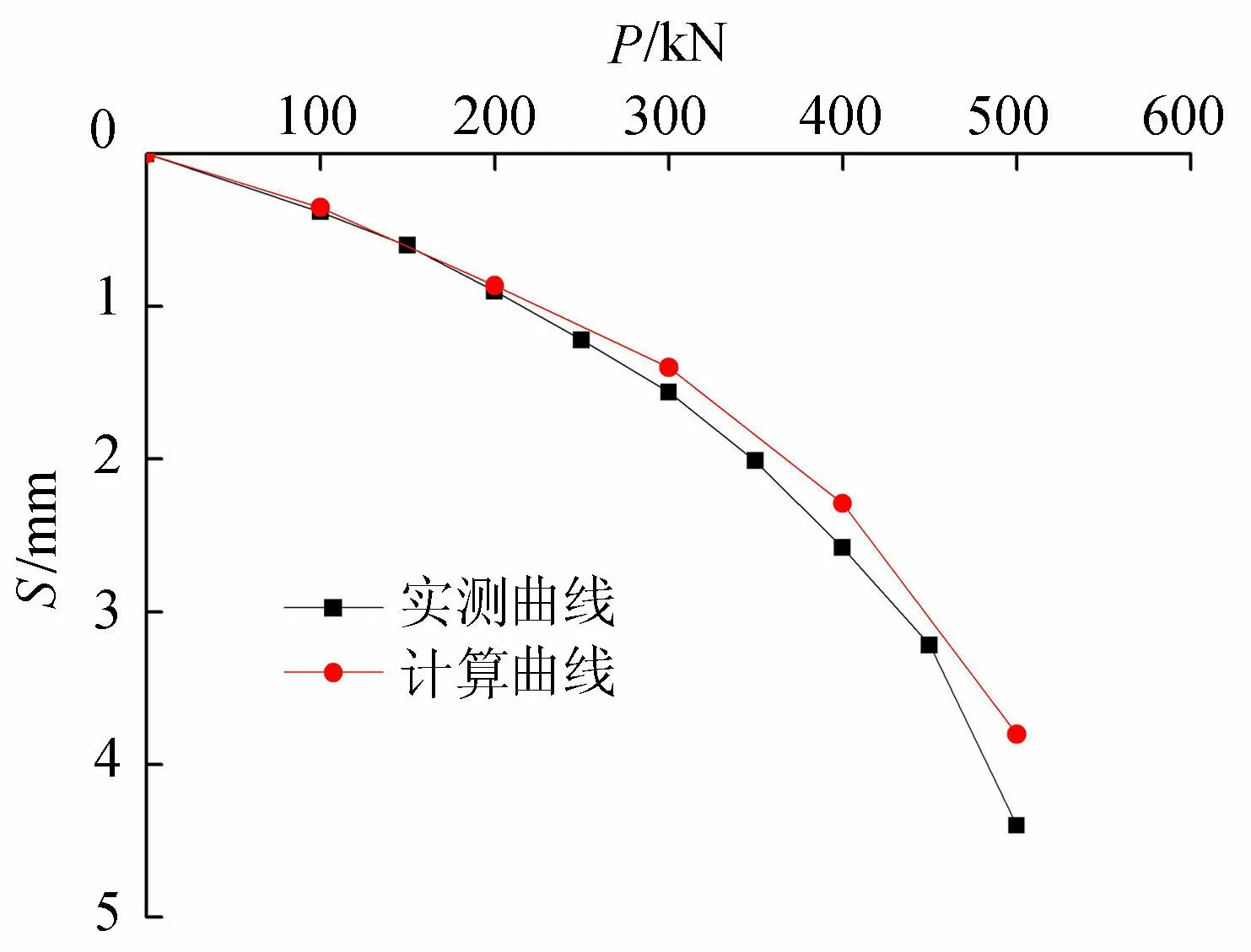
5 结 论
