水下夯锤绕流阻力系数变化规律的数值模拟

黄建生,梁邦炎,王小平

(1.中交第四航务工程局有限公司,广东 广州 510290; 2.中交四航局港湾工程设计院有限公司,广东 广州 510231)



水下夯锤绕流阻力系数变化规律的数值模拟

黄建生1,梁邦炎1,王小平2

(1.中交第四航务工程局有限公司,广东 广州 510290; 2.中交四航局港湾工程设计院有限公司,广东 广州 510231)

基于LS-DYNA流固耦合数值模拟方法,针对多个工程常用锤型进行数值模拟对比,分析了水下夯锤绕流阻力系数变化规律。结果表明:夯锤底面静压强一定时,夯锤质量越大,其绕流阻力系数越小;夯锤在水中下落的过程中,速度随着落距的增加而增大,但增长的幅度逐渐减小并趋于稳定;夯锤的能量利用率随着落距的增加而减小,其中夯锤底面静压强一定时,夯锤质量越小能量耗散率越大。

夯锤;水下运动;绕流阻力系数;能量耗散率

随着我国海洋经济的快速发展,沿海地区以及各海岛上港口护岸工程建设也得到快速发展。重力式码头水下抛石基床的密实施工中,最常采用的两种方法为爆夯法[1]和重锤夯实法[2]。爆夯法施工速度快,然而对周边环境产生的地震效应明显,因此会受周边环境的制约[3];重锤夯实法施工的优点在于施工机动灵活,产生的地震效应对周边建筑物影响小,施工对环境产生的干扰小,缺点在于施工成本高、施工速度慢[4]。为提高工程效益,探求夯锤在水下的绕流阻力系数就十分重要,通过研究水下夯锤绕流阻力系数的变化规律来合理地选取锤型,对提高工程效益有一定的帮助。

目前,国外多采用静压密实方法来测得基床的承载能力,其优点是所得数据可靠,缺点是时间长,经济成本高[5]。国内对抛石基床多采用重锤夯实法密实水下基床,在水下施工条件下不同重锤几何外形与吨位夯实效果差别较大,如何考虑重锤在水下运动过程中的阻力,是重锤选型过程中必需考虑的因素[6]。

本文采用LS-DYNA流固耦合数值模拟方法,针对多个工程常用锤型进行数值模拟对比,分析了绕流阻力系数变化规律,再结合缩比尺室内试验分析绕流阻力系数与夯锤底面静压强的关系,得出夯锤水下运动过程中绕流阻力对有效夯击能的影响规律,可为水下夯锤锤型的选择提供依据。

1 夯锤水下运动规律

图1 夯锤水中受力示意图

夯锤在水中自由下落过程中,受浮力与绕流阻力的影响,存在极限运动速度,有效夯击能随落距的增加而减小,这一过程与夯锤形状、流体性质、流体雷诺数、相对粗糙程度等因素有关。为了分析夯锤在水中自由下落时的运动规律,如图1所示,设夯锤在水中基础上方H处由静止开始下落,当下落距离为x时,作用在夯锤上的力分别为自重mg、浮力F浮和水体阻力Fz。夯锤在三力作用下作加速或匀速运动,夯锤运动方程可表示为

mg-ρwgV-Fz=ma

(1)

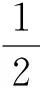
(2)

式中:m为夯锤质量；V为夯锤体积;Fz为运动水体对静止夯锤的绕流阻力;Cf为绕流阻力系数;v为夯锤与水体间相对速度;ω为夯锤垂直于运动方向的投影面积;ρw为水的密度;g为重力加速度。

根据位移x、速度v、加速度a的物理意义,式(1)可进一步整理为

(3)

式中η为质量系数。

研究表明,绕流阻力系数与锤形、流速、流体雷诺数等因素有关[6-9],为简化问题,假设绕流系数为常数,而圆台夯锤的Cf一般介于1.2～1.6之间[10],如果取为定值,则式(3)为二阶常系数微分方程。

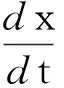
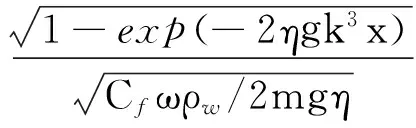
(4)

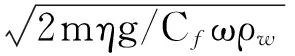
定义夯击能利用率λ为

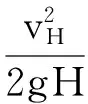
(5)

式中:J′为有效夯击能;J为重力势能或不考虑阻力、浮力达到的最大动能。

因此,在一定落距H下通过绕流阻力系数、夯锤底面积、夯锤质量,即可方便地计算出有效夯击能。但是绕流系数与夯锤形状、水体与夯锤间的相对速度、雷诺数等因素密切相关,在夯锤下落过程中并非定值,常规方法只能借助经验对绕流阻力系数取值。本文采用流体力学分析方法[11-13]通过数值模拟进行不同锤型的运动规律对比分析。

2 数值模型参数

由理论分析可知,夯锤在水中自由下落时,受重力、浮力与绕流阻力的共同作用而作加速运动,且存在一定的极限速度。当水下情况较复杂时,可借助流固耦合法对不同工况下的夯锤运动规律进行数值模拟研究。

流固耦合控制方程遵循最基本的守恒原则,在流固耦合交界面处,满足流体与固体应力τ、位移d、热流量q、温度T等变量的相等或守恒,即满足:

(6)

式中下标f、s分别表示流体和固体。

三维模型的固体部分先建立面,由面拉伸成体,然后进行泄水孔的切割;流体部分先建立一个矩形面,再由面拉伸成正方体,然后对流体边界进行约束,施加无反射边界条件,以此来模拟无限区域的水体[14]。

数值模拟所涉及的力学模型及参数如下:

a. 夯锤选用Johson-Cook塑性模型,该模型的Gruneisen状态方程参数包括:密度ρ=7 850 kg/m3,弹性模量E=210 GPa, 泊松比ν=0.28, 冲击波波速-波后质点粒子速度曲线的截距C=4.57,曲线的斜率系数S1=1.49、S2=0、S3=0,温度常数为1.93。

b. 水体采用Null材料模型,该模型的Gruneisen状态方程参数包括:密度ρ=1 000 kg/m3, 弹性模量E=2.895×10-6GPa, 泊松比ν=0.28,黏滞系数νC=1.01×10-6kPa·s, 冲击波波速-波后质点粒子速度曲线的截距C=1.647，曲线的斜率系数S1=1.921、S2=-0.096、S3=0,温度常数为0.35。

3 工程常用锤型数值模拟

工程中常用的锤型[15]均设置倒角及泄水孔,为了对不同倾角、尺寸的夯锤水下运动规律进行对比,基于工程实践中采用的夯锤尺寸,设计6种锤型,参数如表1所示,计算模型如图2所示。

采用上述6种锤型进行三维模型试验,夯锤在水中落距为10 m,由于实际工况可以是无限水域,为了保证数值模拟与实际工况相符,在模拟夯锤运动时,对水域的边界进行了无反射条件边界设置,保证夯锤在下落过程中,计算水域的宽度对夯锤下落过程可视作无影响[12]。

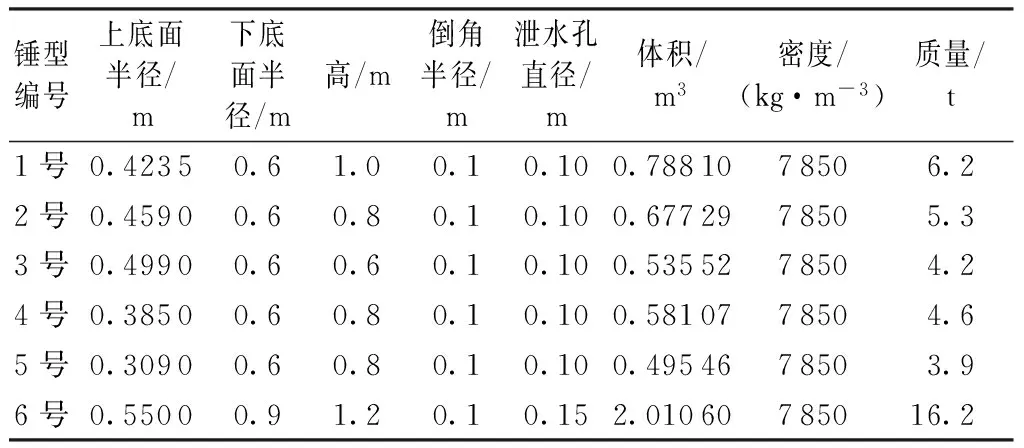
表1 6种锤型的参数取值

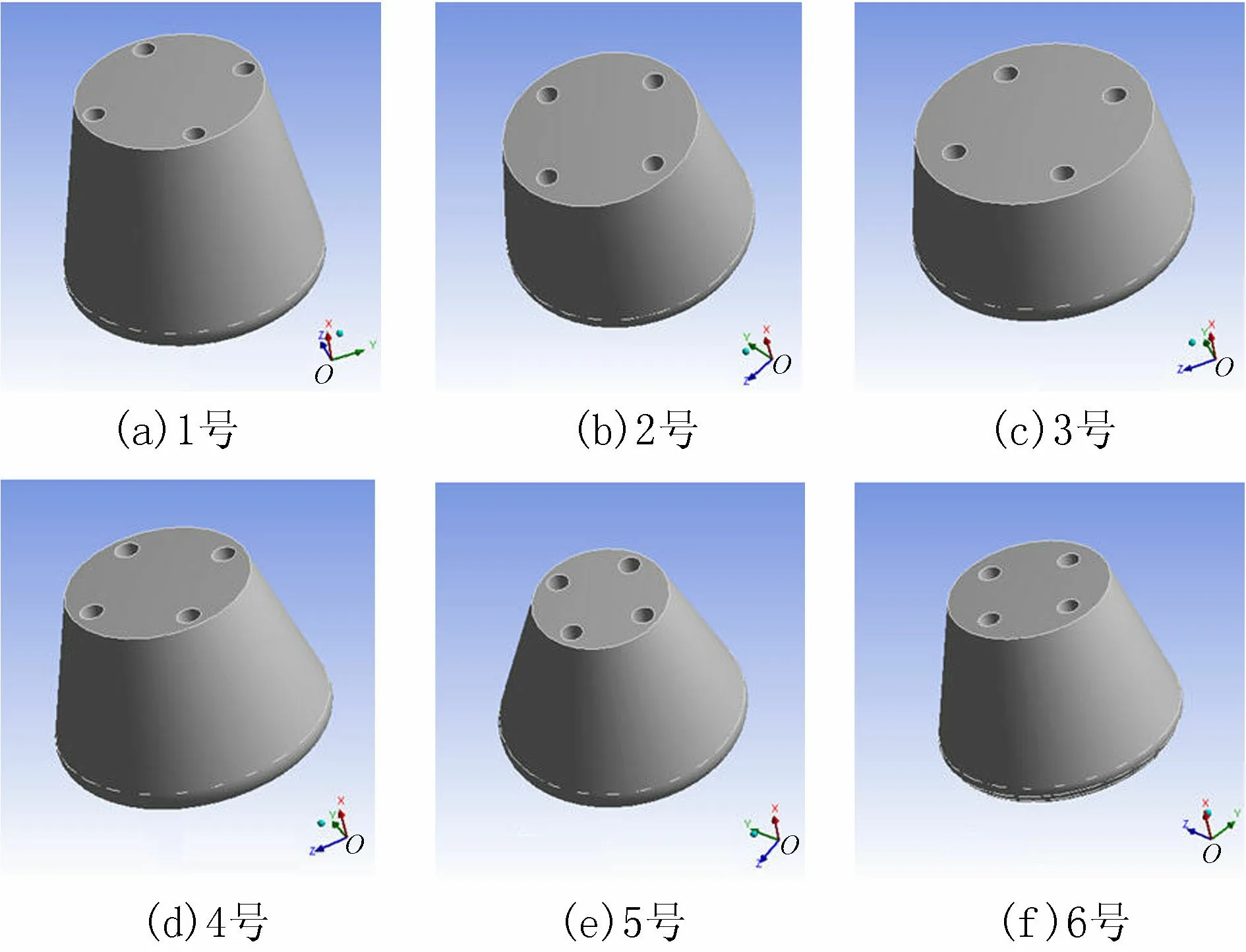
图2 6种锤型的计算模型

为尽量减少网格划分以节约计算时间,同时保证能清晰观察到受夯锤影响水域内的流场情况,结合无条件反射边界设置,多次调试发现水域宽度取5 m即可满足要求,故本文数值模拟时水域宽度取为5 m。

图3为6号锤型下落过程速度云图,可以看出夯锤在下落过程中速度不断增大并趋于一个定值。

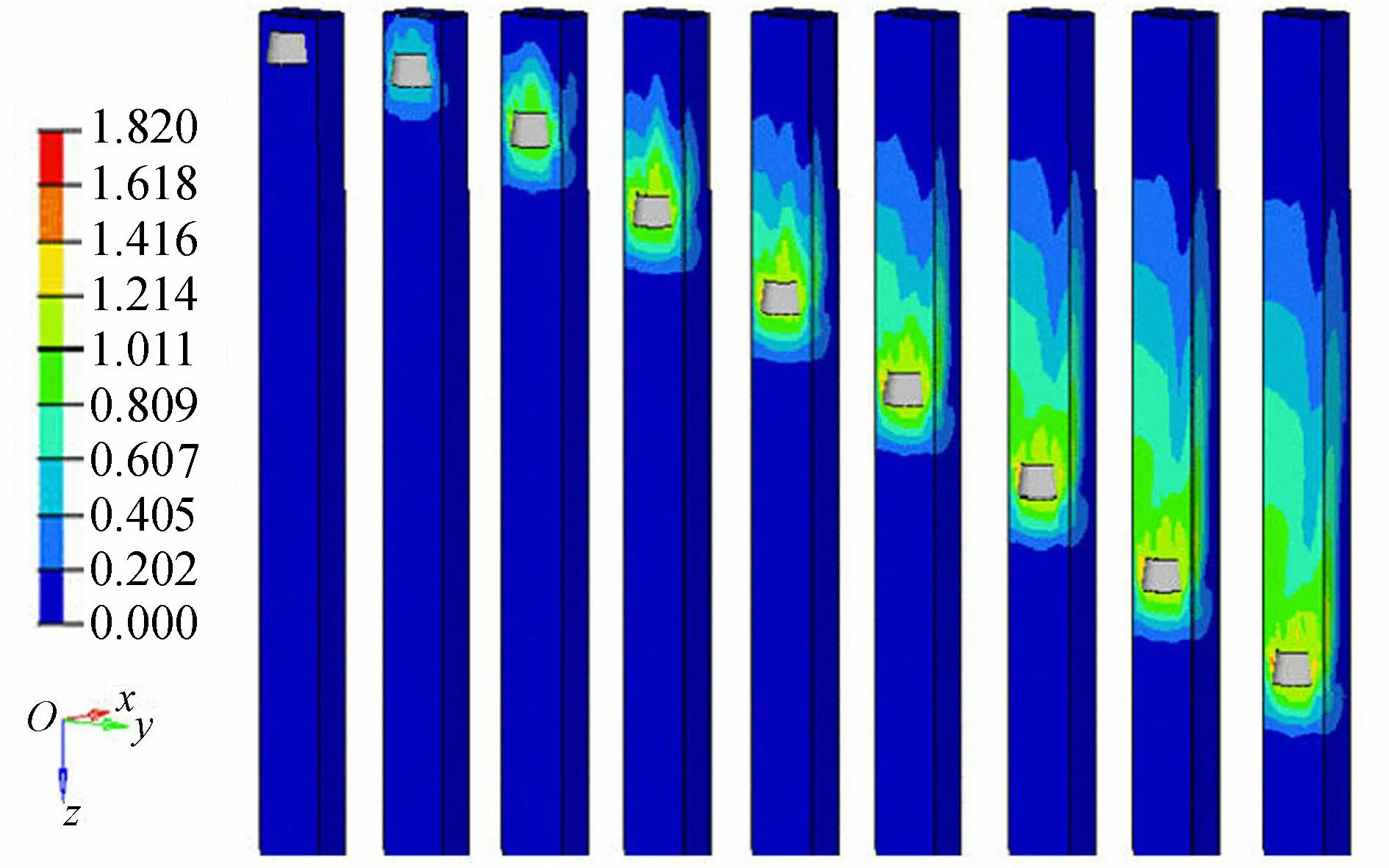
图3 6号锤型下落过程速度云图(单位：m/s)

图4～6分别为6种锤型速度、有效夯击能、夯击能利用率与落距的关系，图7为绕流阻力系数Cf与夯锤底面静压强(锤重力与底面积之比)关系。

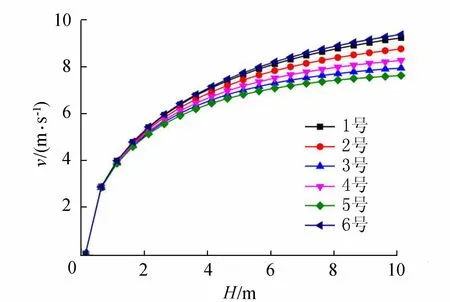
图4 6种锤型速度与落距关系

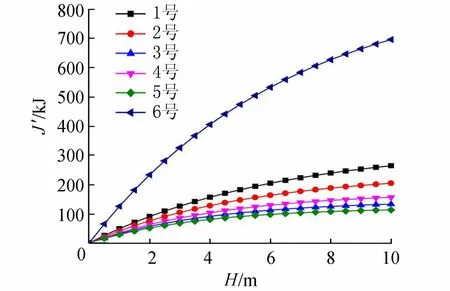
图5 6种锤型有效夯击能与落距关系

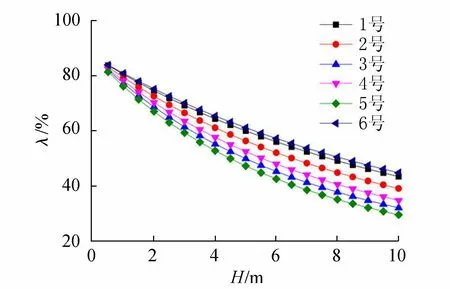
图6 6种锤型夯击能利用率与落距关系

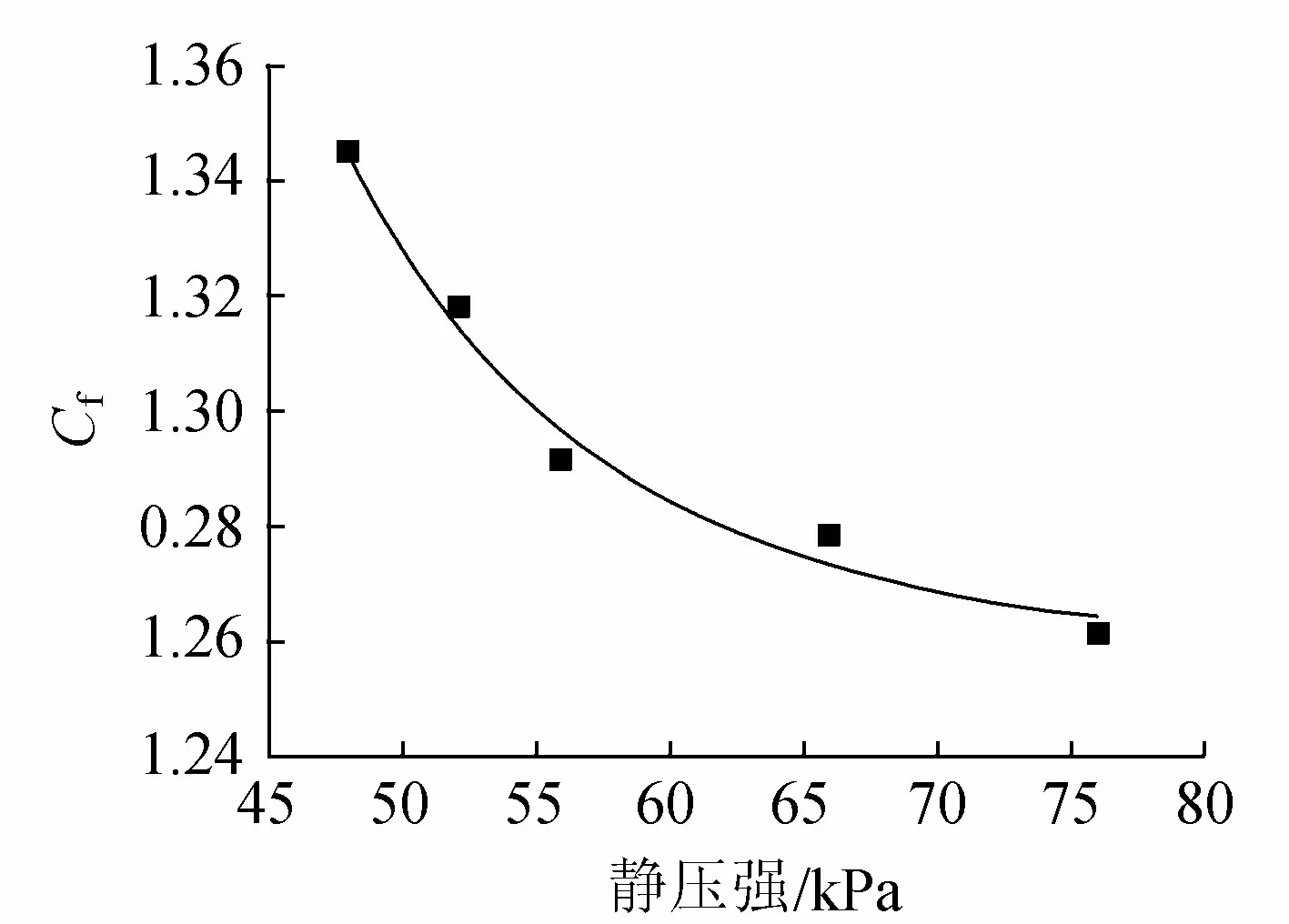
图7 绕流阻力系数与夯锤底面静压强关系

由图4可知,夯锤下落过程中速度逐步增大并逐渐趋于稳定。由图5、图6可知,相同质量夯锤随着落距增加,有效夯击能增大,但夯击能利用率逐渐降低。因此在相同锤质量下,仅通过增大落距,并不能提高夯击能利用率,但在相同底面积、落距等条件下,夯锤质量越大则夯击能利用率越高。由于相同质量夯锤随着落距增加,有效夯击能增大，则由图7可知,随着夯锤底面静压强的增大,绕流阻力系数Cf呈减小后逐渐稳定的趋势,有效夯击能相应增加。

前5个锤型在4 m落距工况下,1号锤型的Cf值最小,为1.255,但其夯击能利用率最高,为63.2%。6号锤型的夯击能利用率为65.5%,略高于1号锤型,但由于质量是1号锤型的3倍左右,其有效夯击能为405 kJ,远高于的1号锤型的153 kJ。对所计算的6种锤型相应Cf值与夯锤质量m之间关系进行拟合,可得

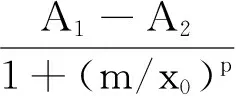
(7)

各参数取值为：A1=3.250 51，A2=1.167 76,x0=0.865 03，p=1.631 8。根据拟合公式计算得到相关实际工程中1～6号锤型的Cf值分别为1.252～1.255、1.273～1.276、1.322～1.324、1.289～1.292、1.356～1.359和1.185～1.191。

4 夯锤缩比尺对比

表2为缩比尺室内试验标准、5倍、10倍和15倍锤型参数(均为三轴同时放大相同倍数,包括泄水孔)。

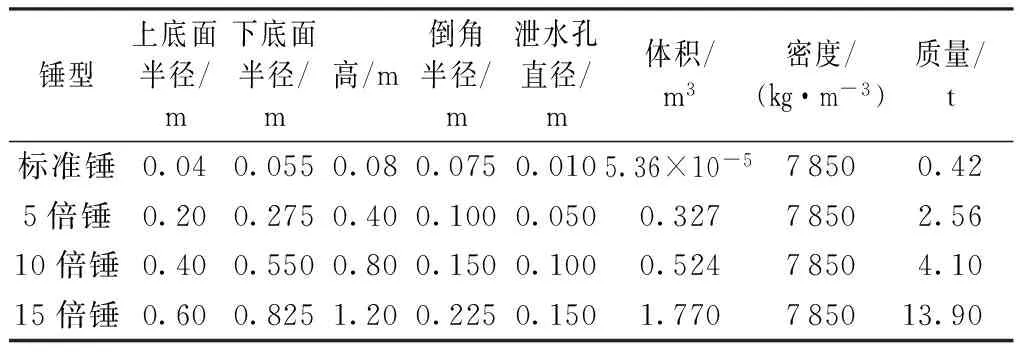
表2 标准、5倍、10倍和15倍锤型的参数取值

缩比尺数值模拟采用的标准、5倍、10倍和15倍锤的计算模型如图8所示，在相同条件下计算模拟所得的速度与落距关系如图9所示,夯击能利用率与落距关系如图10所示。

图8 夯锤缩比尺计算模型

图9 缩比尺锤速度与落距关系

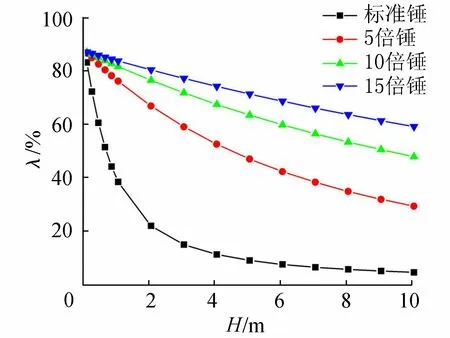
图10 缩比尺锤夯击能利用率与落距关系

由图9和图10可见:夯锤落距相同时,随着夯锤质量的增大,速度相应增大,质量越小,能量耗散越快。如标准锤在下落1 m左右时速度就接近稳定(与室内试验结果几乎一致),夯击能量利用率就下降到一半,可见质量对夯锤下落的影响非常明显。

(3)只要我们稳扎稳打，踏踏实实地进行艰苦细致的工作，我们就一定能够一步一步地达到自己的目的。(1991年)

标准锤运动规律试验与数值计算结果对比如图11所示,可见数值模拟结果与室内试验结果相差很小,总体速度稍大。

图11 标准锤室内试验与数值模拟速度与落距关系

数值模拟得到Cf=1.492,与室内试验值(1.5)较为接近,说明数值模拟所得到的结果具有一定的合理性。通过缩比尺数值计算得到标准、5倍、10倍和15倍锤的Cf取值范围分别为1.491～1.495、1.474～1.481、1.401～1.412和1.321～1.334,说明夯锤静压强一定时,Cf不是定值,随着夯锤质量的增大,Cf呈下降趋势，夯锤质量在Cf的取值过程中有重要影响。

5 结 论

a. 相同质量夯锤随着落距增加,夯击能增大,夯击能利用率逐渐降低,但夯击速度逐渐趋于稳定。因此在相同夯锤质量条件下,仅通过增大落距并不能提高夯击能利用率,但在相同底面积、落距等条件下,夯锤质量越大则夯击能利用率越高。

b. 随着夯锤底面静压强的增大,夯锤绕流阻力系数Cf呈逐渐减小的趋势,最后趋于稳定。相同质量夯锤随着落距增加,夯击能增大;随着夯锤质量的增大,相应的有效夯击能相应增大。

c. 缩比尺数值模拟结果表明,落距相同时,随着夯锤质量的增大,速度相应增大。夯锤底面静压强一定时,夯锤质量越小能量耗散越快,但Cf仍为不确定值,随着夯锤质量的增大Cf呈下降趋势。

[ 1 ] 李俊如,高建光,贺涛,等.广西钦州港二期码头抛石基床的水下爆夯[J].岩土力学,2004,24(6):917-921.(LI Junru,GAO Jianguang,HE Tao,et al.Strengthening foundation by underwater explosive ramming for second phase dock of Qingzhou Harbor in Guangxi Region[J].Rock and Soil Mechanics,2004,24(6):917-921.(in Chinese))

[ 2 ] 冯世晖,庞善喜.重力式码头基础施工过程控制[J].水运科学研究,2007(2):21-24.(FENG Shihui,PANG Shanxi.Process control on foundation construction for gravity wharf[J].Research on Waterborne Transportation,2007(2):21-24.(in Chinese))

[ 3 ] 蔡劼刚.用爆破夯实法处理水下拋石基床[J].港口工程,1990(5):26-28.(CAI Jigang.Rubble mound foundation with blasting tamping[J].Port Engineering,1990(5):26-28.(in Chinese))

[ 5 ] 童新春, 叶锋,邱青长，等,重力式码头抛石基床重锤夯实施工效率改进研究[J].水运工程,2013(3):199-203.(TONG Xinchun,YE Feng,QIU Qingchang,et al.Method for improving the efficiency of heavy tamping compaction of gravity wharf’s rubble bed[J].Port & Waterway Engineering,2013(3):203-199.(in Chinese))

[ 6 ] 滕丽娟,张志伟,武燕蕾.湍流模型下双柱绕流升阻力系数数值模拟[J].河北工程大学学报(自然科学版),2009, 26(2):51-54.(TENG Lijuan,ZHANG Zhiwei,WU Yanlei.Simulation of drag and lift coefficients on two cylinders in flow field with turbulence model[J].Journal of Hebei University of Engineering(Nature Science of Edition),2009,26(2):51-54.(in Chinese))

[ 7 ] 金大桥,王聪,魏英杰,等.水下圆柱体带空泡轴向绕流研究[J].哈尔滨商业大学学报(自然科学版), 2010, 26(5):586-591.(JIN Daqiao, WANG Cong, WEI Yingjie,et al.Axial cavitating flow study of underwater circular cylinder[J].Journal of Harbin University Commerce(Nature Science of Edition),2010, 26(5):586-591.(in Chinese))

[ 8 ] 陈凯华,石崇,梁邦炎,等.水下抛石基床动态形成过程数值模拟研究[J].科学技术与工程,2014,31(14):314-319.(CHEN Kaihua,SHI Chong,LIANG Bangyan,et al.Numerical simulation research of the falling process for the underwater ripraps[J]. Science Technology and Engineering,2014,31(14): 314-319.(in Chinese))

[ 9 ] ZHU L,WANG J,CHENG N S,et al.Settling distance and incipient motion of sandbags in open channel flows[J].American Society of Civil Engineers,2014,130(2):98-103.

[10] 王德利.不同夯锤的水下夯实效果及夯锤阻力理论在水下夯实中的运用探讨[J].水运工程,1990(3):51-53.(WANG Deili.Different rammer underwater compaction effect and tamper resistance theory in the application of underwater ramming[J].Port & Waterway Engineering,1990(3):51-53.(in Chinese))

[11] 韩世娜.空心块体水流拖曳力的试验研究[D].南京:河海大学,2007.

[12] 陈玉璞.流体动力学[M] 北京:清华大学出版社,2013:201-207.

[13] COLEMAN S E,MELVILLE B W,GORE L.Fluvial entrainment of protruding fractured rock[J].Journal of Hydraulic Engineering,2014,129(11):872-884.

[14] HIRT C W,NICHOLS B D.Volume of fluid(VOF) method for the dynamics of free boundaries[J].Journal of Computational Physics,1981,39:201-225.

[15] 谢立全,戚健文,盛旭圆,等.水下抛石基床重锤夯实及夯锤工作性能数值分析[C]//夏才初.和谐地球上的水工岩石力学:第三届全国水工岩石力学学术会议论文集.上海:同济大学出版社,2010:504-508.

Numerical simulation of change in flow resistance coefficient of underwater hammer

HUANG Jiansheng1, LIANG Bangyan1, WANG Xiaoping2

(1.CCCC Fourth Harbor Engineering Co., Ltd., Guangzhou 510290, China; 2.Harbor Engineering Design Institute of CCCC Fourth Harbor Engineering Co., Ltd., Guangzhou 510231, China)

Change in the flow resistance coefficient of underwater hammers was analyzed through comparison of common types of hammers in multiple projects based on the LS-DYNA fluid-structure coupling numerical simulation method. The results show that, when the hydrostatic pressure on the bottom surface of the hammer is a fixed value, the flow resistance coefficient decreases with the increase of the hammer mass. The hammer fall velocity in the water increases with the drop distance, but the growth rate gradually decreases and tends toward a stable value. The energy usage ratio of the hammer decreases with the increase of the drop distance. When the hydrostatic pressure on the bottom surface is a fixed value, the energy dissipation rate increases with the decrease of the hammer mass.

hammer; underwater movement; flow resistance coefficient; energy dissipation rate

黄建生(1960—),男,高级工程师,主要从事港口工程施工技术管理工作。 E-mail:hjiansheng@cccc4.com

梁邦炎(1981—),男,高级工程师,主要从事水工结构研究。E-mail:81519381@qq.com

10.3880/j.issn.1006-7647.2017.04.003

TV131.2+2

A

1006-7647(2017)04-0014-05

2016-08-15 编辑：熊水斌)