基于FLAC3D多裂隙模型的层状岩质边坡破坏特征及稳定性

鲁海峰,姚多喜,胡友彪,郭 鹏

(安徽理工大学地球与环境学院,安徽 淮南 232001)



基于FLAC3D多裂隙模型的层状岩质边坡破坏特征及稳定性

鲁海峰,姚多喜,胡友彪,郭 鹏

(安徽理工大学地球与环境学院,安徽 淮南 232001)

采用FLAC3D多裂隙本构关系,建立层状岩坡平面破坏特征的各向异性数值分析模型。运用强度折减法,得出边坡安全系数与层间弱面倾角β、坡角α、坡高H以及岩体抗剪强度之间的关系,并采用灰色关联法给出了各因素对安全系数的影响程度。研究结果表明:顺倾向边坡,当β≤15°时,其破坏形式主要是拉裂-剪切-滑移破坏,滑面不沿层间弱面;当15°<β<α时,产生顺层滑移破坏;当β≥α时,坡顶处沿弱面滑移,坡角处弯折破坏。反倾向边坡,当β<50°时主要为压剪破坏,β较大时(β≥50°)为倾倒破坏。随着β的增大,顺倾向边坡的安全系数呈先减、后增、再减的趋势,且水平层状边坡的稳定性要高于直立边坡;反倾向边坡的安全系数变化趋势与顺倾向边坡相反。当β>α时,顺倾向边坡的稳定性要高于同倾角的反倾向边坡。顺倾向边坡,坡高对其稳定性影响最大,其次为弱面黏聚力和坡角,而弱面倾角和弱面摩擦角相对影响较小； 反倾向边坡,各因素对其稳定性的影响程度依次为弱面摩擦角、坡角、坡高、弱面黏聚力和弱面倾角。

多裂隙模型;层状岩质边坡;稳定性;强度折减

岩质高边坡失稳是重大地质灾害之一,准确分析其破坏特征并给出稳定安全系数是边坡治理中的一个关键问题。层状岩质边坡在各类边坡工程中占有很大比例,由于组成该类边坡的层状岩体存在着一组优势定向结构面,导致其力学性质呈现明显的各向异性,使得边坡稳定性问题变的十分复杂[1-2]。

实际工程中,理论分析与数值模拟被普遍运用到层状岩质边坡稳定性分析中。理论分析方面,汪小刚等[3]考虑岩体结构面连通率,建立了层状边坡倾倒破坏的极限平衡分析方法;伍法权[4]运用岩体力学理论对云母石英片岩斜坡弯曲倾倒变形进行了分析;刘小丽等[5]依据弹性薄板理论,利用能量法对顺层岩质边坡的溃曲失稳机制进行了分析;邓荣贵等[6]根据顺层边坡的结构特征,对其失稳的临界长度进行了研究;朱晗迓等[7]建立了多层层状岩质边坡的溃屈破坏曲线的理论公式,求出了各层溃屈的理论公式。数值分析方面,冯君等[8]运用有限元方法对顺层岩质边坡稳定性的影响因素进行了分析,指出当边坡走向与岩层走向夹角超过30°后,边坡发生顺层滑动破坏的可能性很小;吴顺川等[9]运用FLAC3D,基于强度折减法,对顺层边坡的稳定性进行了分析;蒋青青等[10]采用FLAC3D,分析了层理倾角、倾向与边坡稳定性之间的关系;林杭等[11]采用FLAC3D,结合强度折减理论分析了结构面倾角与边坡稳定性之间的关系;卢敦华等[12]探讨了结构面强度参数对层状边坡稳定性及滑动模式的影响规律;阎石等[13]使用FLAC3D对顺层岩质高边坡稳定性进行了数值模拟分析。

上述研究成果在不同时期不同程度上对层状岩质边坡的稳定性预测起到了积极的指导作用，但针对层状岩质边坡的破坏特征以及稳定性影响规律的系统研究还不多见。由于理论分析一般需要假定层状边坡的破坏形式,且不能有效地反映层状岩体的变形破坏机制及其发展过程，基于此，本文利用FLAC3D及软件自带的多裂隙本构模型来描述层状岩体的各向异性力学特性,系统地研究层状岩质边坡的平面破坏模式及其特征,分析结构面倾角β、坡角α、坡高H以及抗剪强度等因素对边坡稳定性的影响,并采用灰色关联理论给出了各因素对边坡稳定的关联度,研究成果可为工程实践提供指导。

1 数值计算模型

1.1 本构模型的选择

层状岩体数值计算时,关于弱面的作用,一种方法是用接触面单元来模拟,如蒋青青等[10]运用该法分析了层状边坡的破坏模式。这种方法物理意义明确,且能很好地描述层状岩体在弱面处的不连续性,但只适合模型中弱面数较少的情况,如果层状岩体层间结构面密集,该法很难应用。另一种方法是将层状岩体等效成一个具有各向异性特征的连续体,建立一个合适的本构模型来描述这种特征。FLAC3D内嵌的多裂隙本构模型正是基于此思想,该模型在Mohr-Coulomb本构模型中加上一个定向弱面,同样依据Mohr-Coulomb剪切和拉伸屈服准则,可同时考虑层状岩体中的岩块和弱面的力学属性。根据应力状态、弱面产状以及岩块和弱面材料特性的不同,屈服可能发生在岩块内,或者发生在弱面上,或者在两个部分都发生[14]。故该模型可用来模拟层状岩体的各向异性破坏特征。

层状岩体中的岩块模拟部分可参考文献[14]的Mohr-Coulomb本构模型,以下将主要介绍弱面的数值实现。对于弱面,依据其倾角和方位角设置局部坐标系Ox′y′z′如图1所示。局部坐标和整体坐标的关系可由柯西转轴公式实现[15]。

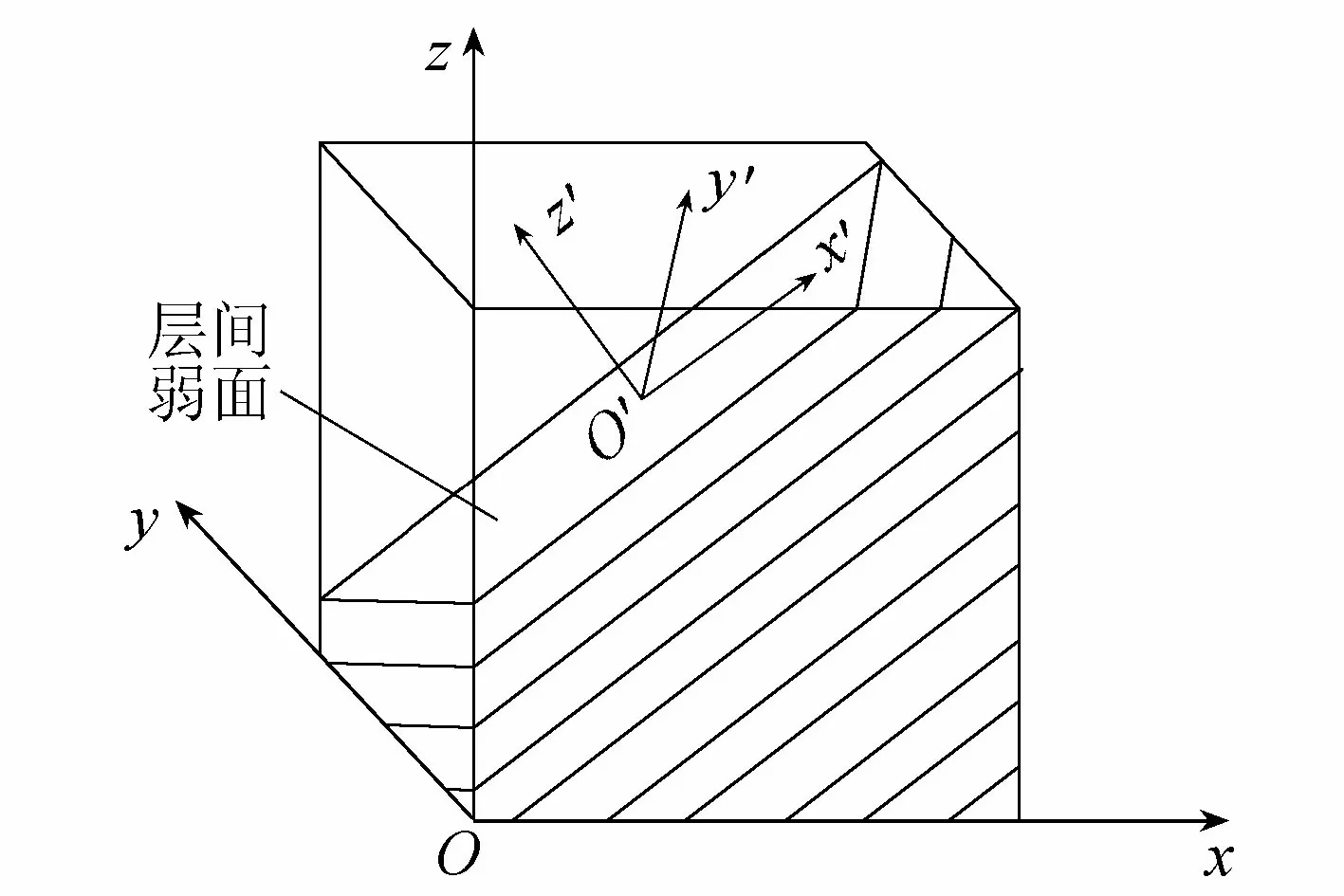
图1 层状岩体中弱面的局部坐标

如图2所示，在τ-σ3′3′坐标下剪切破坏判别式fs(线段AB)和拉伸破坏判别式ft(线段BC)形式分别为

fs=τ+σ3′3′tanφj-cj

(1)

ft=σ3′3′-σtj

(2)

式中:φj、cj、σtj分别为弱面的内摩擦角、黏聚力和抗拉强度;σ3′3′为弱面上的法向应力。

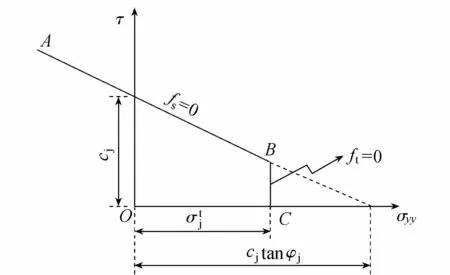
图2 弱面屈服准则

根据式(1),当弱面应力状态进入屈服区域时,根据流动法则,需要对应力进行修正。在该模型中,剪切破坏应力gs采用非关联流动法则(式(3)),而拉破坏应力gt采用的是关联流动法则(式(4)):

gs=τ+σ3′3′tanψj

(3)

gt=σ3′3′

(4)

式中ψj为弱面膨胀角。

如图2所示,在剪切破坏AB阶段,剪切修正后的应力应满足屈服准则式(1)，则根据塑性理论,t时刻弱面上应力σoi′和t+Δt时刻应力σNi′应满足:

(5)

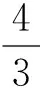
式中:K为剪切模量;G为体积模量;Si为弹性应力-应变线性关系。由式(5)即可获得经剪切修正后的应力增量Δσi′=σNi′-σoi′。

对拉伸破坏BC阶段,拉伸修正后的应力应满足屈服准则式(2)。同理可得拉伸修正后的应力增量为

(6)

需指出的是,以上弱面应力修正是在局部坐标系Ox′y′z′里进行的,最后应将其转换到整体坐标系Oxyz下。

1.2 安全系数的获取

边坡稳定安全系数采用强度折减法来获得。在多裂隙本构模型中,描述岩体的抗剪强度参数分别为岩块的黏聚力c、内摩擦角φ和弱面的黏聚力cj、内摩擦角φj。参考常规的Mohr-Coulomb模型的折减方法,多裂隙模型可按照式(7)来改变岩块和弱面的抗剪强度参数,并对边坡的稳定性进行数值分析。不断加大折减系数,重复模拟直至计算无法收敛,达到边坡的临界破坏状态,此时得到的折减系数就是安全系数Fs。

(7)

式中cF、φF、cjF、φjF分别为折减后的岩块黏聚力、内摩擦角、弱面黏聚力、弱面内摩擦角。

1.3 计算范围、边界以及材料参数

数值模型的边界按张鲁渝等[16]的研究成果,即坡顶至右边界的距离为2.5H,坡顶部到底部边界的距离为2H;右边界至坡角的距离为1.5H。本文主要研究层状岩质边坡的平面破坏,采用平面应变模型。坡角55°的模型及网格剖分如图3所示。

图3 数值计算模型

边界条件为上部自由,下部固定,左右两侧水平约束。初始应力场由岩体自重产生。计算收敛准则为不平衡力比率小于10-5,如果不能满足,则计算上限步数为4万步。边坡岩体参数如表1所示。

表1 多裂隙模型材料参数

2 模拟结果分析

2.1 层状岩质边坡破坏形式

层状岩质边坡的稳定性受岩层走向与坡面走向的夹角、弱面倾角β与坡角α的比值、岩体强度、坡高H、坡角α等因素控制，其中,层状岩质边坡的平面破坏形式主要与弱面倾角相对坡角的大小有关。为描述方便,将β为0°的水平层状边坡和90°的直立边坡统一划分为顺倾向边坡,即岩层倾向与坡向一致;反之则为反倾向边坡(β=0°～90°)。以坡角α=55°、坡高H=60 m为例,不断改变弱面倾角β(变化梯度为5°)分别探讨层状边坡的破坏形式。边坡滑面的判定依据位移等值图,即当边坡达到临界失稳状态时,滑体位移将远大于稳定体的位移,故可根据其分界线来判定滑面。

图4为当0°≤β≤15°时的边坡临界失稳时的位移等值线图。从图4可以看出,由于弱面倾角远小于坡角,一般不产生顺层滑动。该类边坡在重力下滑分力作用下,坡顶破坏形式为拉裂破坏,形成张拉裂缝,裂缝上大下小[11]。随着张裂缝的加大,滑体在坡角处顺层滑出。故该类边坡的破坏形式为拉裂-压剪-滑移形式。

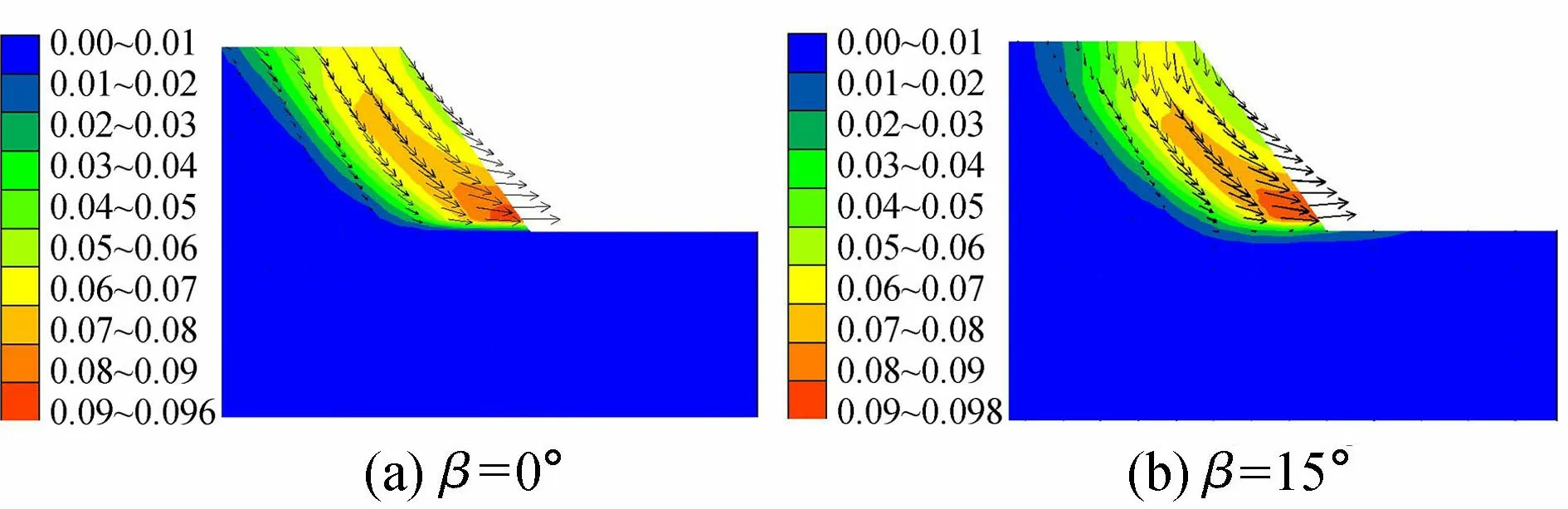
图4 低倾角顺倾向边坡的破坏模式(单位:m)

随着弱面倾角的加大,当20°≤β≤α时,由于弱面倾角小于坡角,边坡面将坡角处岩层弱面切断,形成剪出口,其破坏形式一般是沿弱面发生顺层滑移破坏,如图5所示。边坡极限状态时的位移等值线基本平行于岩层弱面,表现为滑体的顺层滑动。

图5 顺倾向边坡的顺层滑动破坏(β<α,单位:m)

当α≤β≤90°时,在边坡上部,层状岩体在自重作用下一般会产生顺层滑移。由于弱面倾角大于坡角,岩层弱面在坡面处形成临空面,而在坡面处不形成剪出口,导致滑体在坡角处发生弯曲变形;当岩体承受的应力超过其强度时,滑体出现折断破坏,沿弯折破碎带剪出,最终表现为溃屈折断破坏,如图6所示。溃屈程度取决于岩体强度和刚度、弱面倾角、坡角等因素的影响[7,11]。

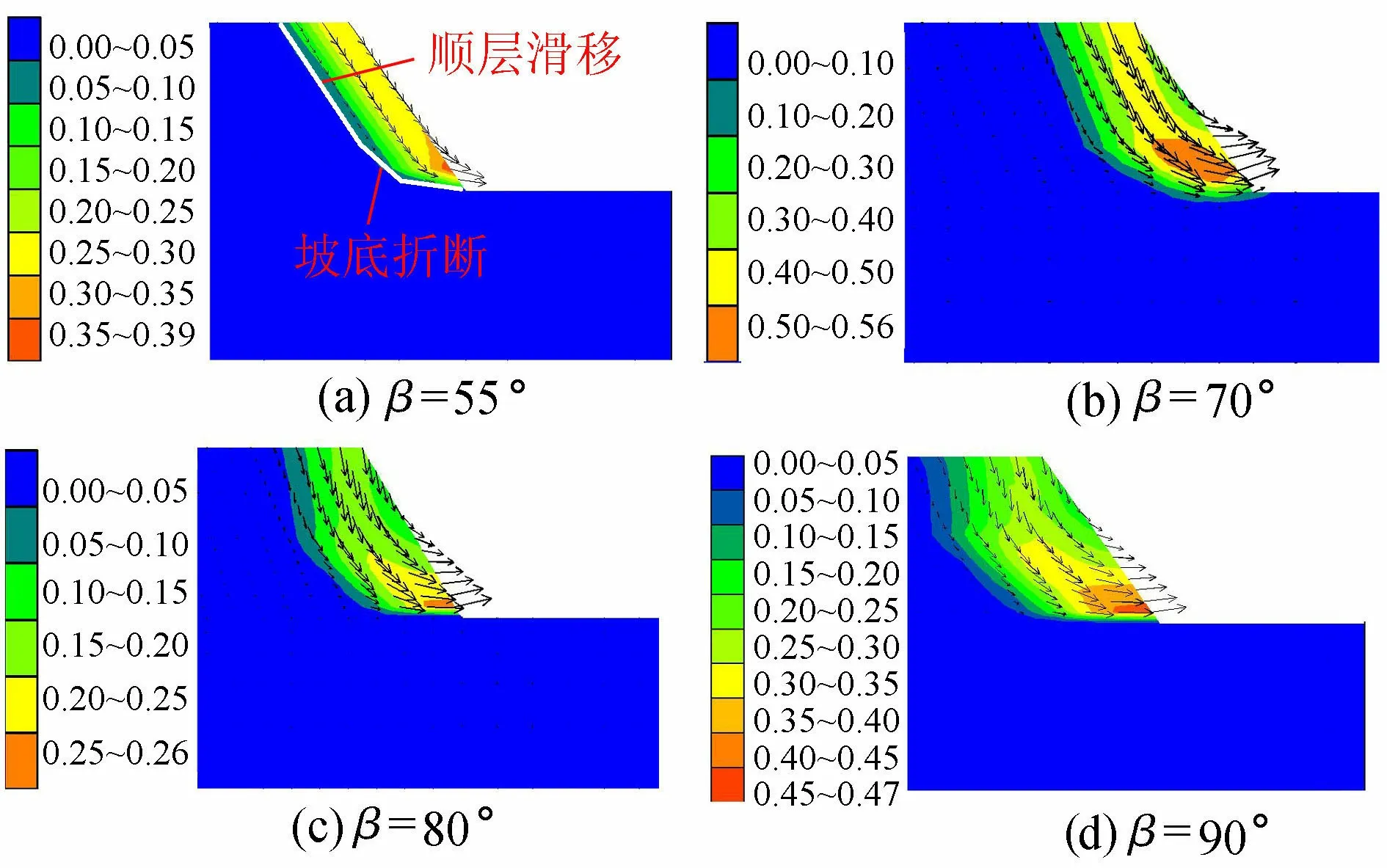
图6 顺倾向边坡的顺层滑移-折断破坏(β≥α,单位:m)

对于反倾向边坡，当弱面倾角较小时(β<50°),即岩层倾角较小,此时岩层在重力作用下,反倾向岩体向边坡临空面产生的弯矩值较小,一般不易产生弯曲变形。在重力下滑分量作用下,滑体在坡下部剪切穿层滑出,其破坏形式为压剪型破坏,如图7所示。

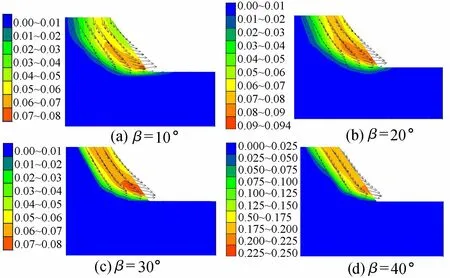
图7 低倾角反倾向边坡的压剪破坏(单位:m)

当弱面倾角β≥50°时,反倾向边坡将发生倾倒破坏,如图8所示。同时从图8可以看出,当β达到70°时,反倾边坡在其顶部出现拉张裂缝,随着β的增大,上部岩层向临空面产生弯矩变大,势必导致拉裂缝范围和深度扩大,边坡更易发生倾倒破坏,如图8(c)(d)所示。

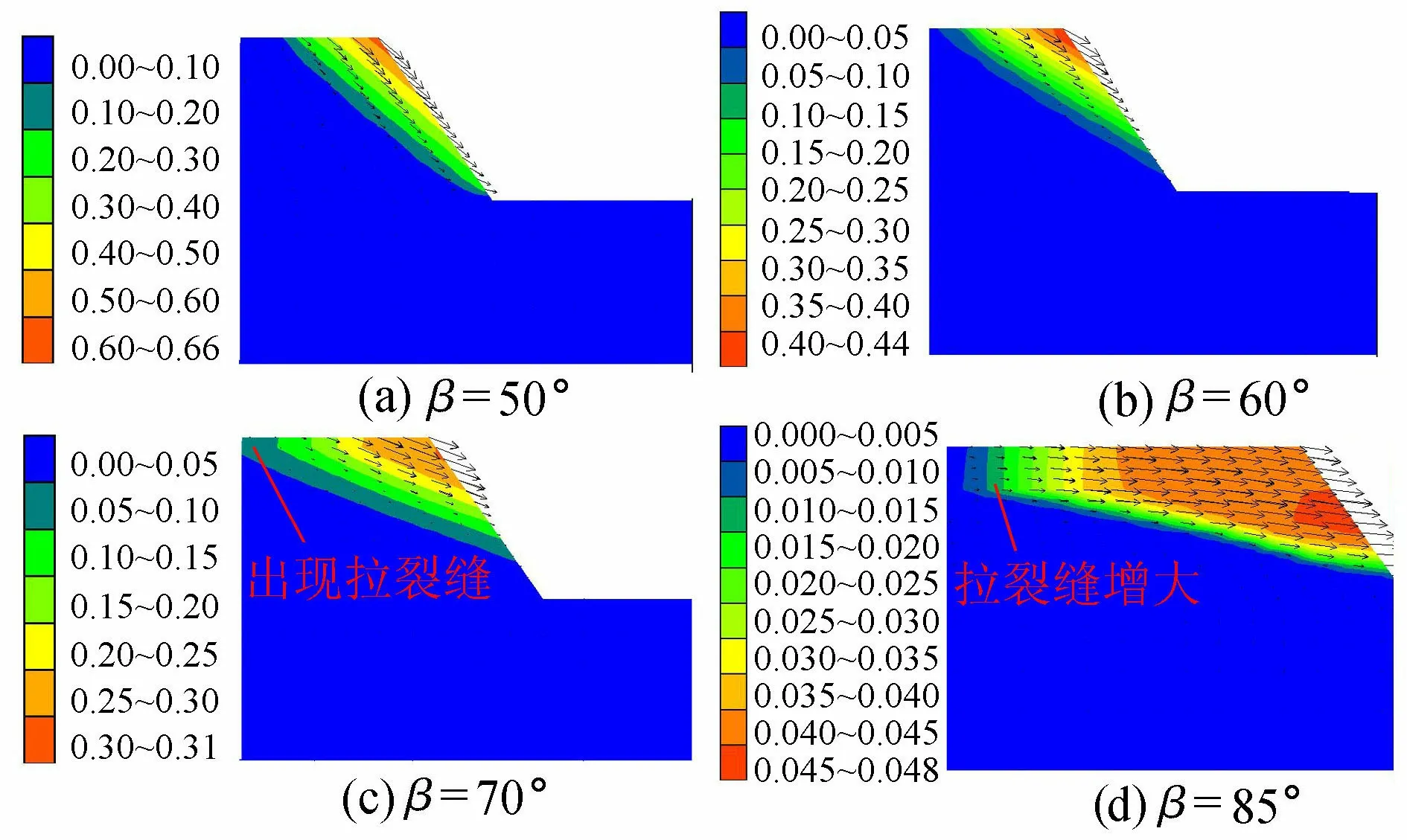
图8 高倾角反倾向边坡的倾倒破坏(单位:m)

2.2 各因素对边坡稳定安全系数的影响

2.2.1 弱面倾角的影响

以坡高H=60 m、坡角α=55°为例,边坡稳定安全系数Fs与弱面倾角β的关系如图9所示。从图9可以看出,随着β的增大,顺倾向边坡的安全系数呈先减、后增、再减的趋势,在β=30°左右时,安全系数值最低。同时可看出,水平层状边坡的稳定性要高于直立边坡;而反倾向边坡的安全系数变化趋势与顺倾向边坡相反。当β>α时,顺倾向边坡的稳定性要高于同倾角的反倾向边坡。这是由于当β≥α时,顺倾向边坡的破坏模式由顺层滑移转变为溃屈折断破坏,而反倾向边坡的破坏模式由压剪转变为倾倒破坏。随着β的增大,上部岩层向临空面产生弯矩变大,边坡更易发生倾倒破坏。

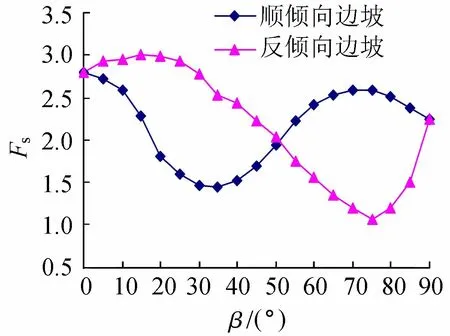
图9 安全系数与弱面倾角关系

2.2.2 坡高的影响

以坡角α=55°、弱面倾角β=60°的边坡为例,安全系数随坡高H的变化情况如图10所示,计算时H在30～70 m之间(间隔5 m)变化。从图10可以看出,随着坡高的加大,无论顺倾向还是反倾向边坡,其安全系数均呈非线性形式递减。

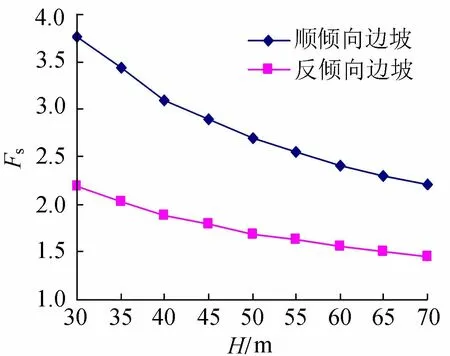
图10 安全系数与坡高的关系

2.2.3 坡角的影响

为研究坡角α的大小对边坡稳定的影响,以坡高H=60 m、弱面倾角β=60°的边坡为例,安全系数随坡角α的变化情况如图11所示,其中α在30°～90°(间隔5°)之间变化。从图11可以看出,坡角越大,安全系数越小,即边坡越陡其稳定性越差。

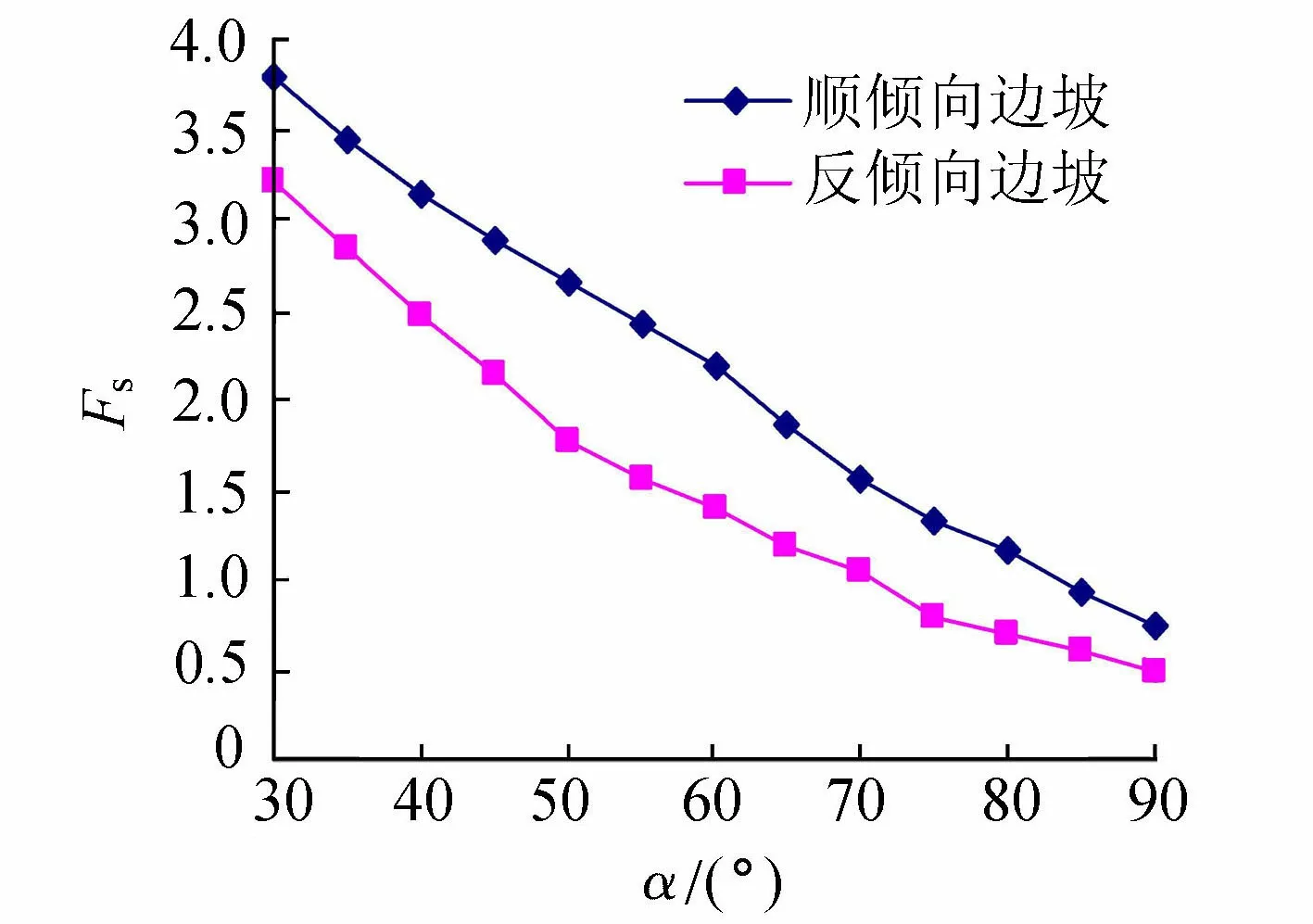
图11 安全系数与坡角的关系

2.2.4 弱面抗剪强度的影响

以坡高H=60 m、坡角α=55°、弱面倾角β=60°的边坡为例,其余强度参数固定不变,分别改变弱面黏聚力和内摩擦角,其中黏聚力变化于0.01～0.1 MPa区间(变化梯度为0.01 MPa),内摩擦角变化于12°～30°区间 (变化梯度为2°),得到边坡安全系数和弱面抗剪强度之间的关系如图12所示。从图12可以看出,随着弱面抗剪强度的增大,安全系数越大,表明边坡越趋于稳定,且二者同样近似呈线性关系。

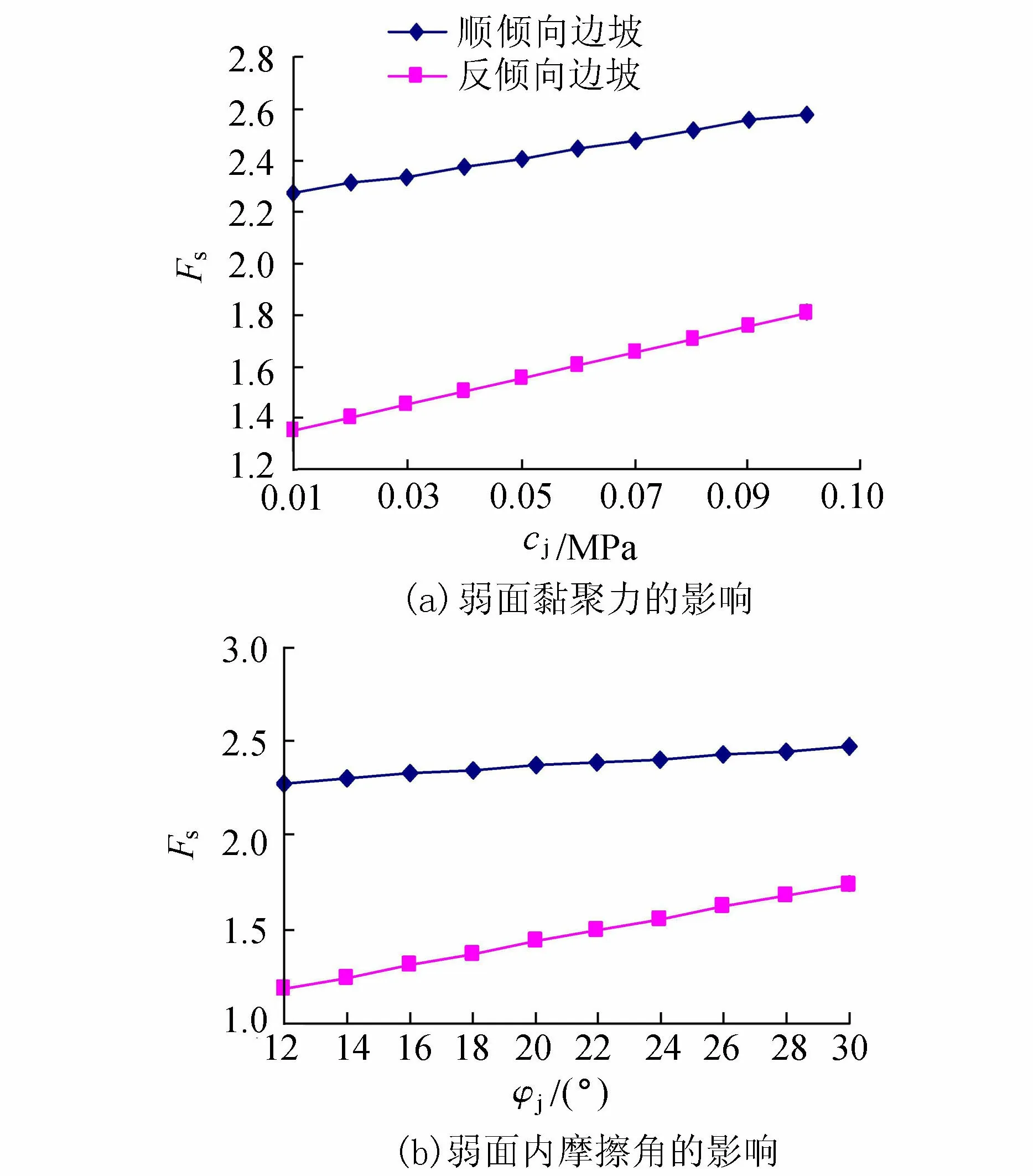
图12 安全系数与弱面抗剪强度的关系

3 层状岩质边坡稳定性影响因素的灰色关联排序

在以上分析的层状岩质边坡稳定性影响因素中,为分析各影响因素影响程度,采用灰色关联理论对各影响因素进行排序。

灰色关联分析用来衡量因素间的关系程度、子因素对母因素的贡献程度,其基本原理为[17],设有一母因素数列,记作X0≡{X0,1,X0,2,…,X0,n},同时又有一系列子因素数列,X1、X2、…、Xm,记作:

X1≡{X1，1,X1，2,…,X1，n}

(8)

X2≡{X2，1,X2，2,…,X2，n}

(9)

⋮

Xm≡{Xm,1,Xm，2,…,Xm，n}

(10)

记Xi(i=1,2,…,n)对X0在K采样点的关联系数为L0i,k,则:

(11)

式中:Δmin为因素间最小绝对差;Δmax为比较点上因素间的绝对差;ρ为分辨系数,一般取0.5。

由于关联系数较多,信息分散,不利于实际比较,为此,可采用Xi对X0的关联度r0i来比较子因素对母因素的关联程度:

(12)

从式(12)可看出,关联度r0i值越大,子因素对母因素的影响程度也就越大。

依据上述原理,根据各因素影响下的顺倾向和反倾向层状边坡安全系数值,可得出顺倾向和反倾向边坡的坡高、坡角、弱面倾角、层间弱面黏聚力以及内摩擦角的灰色关联度r0i分别为0.811、0.793、0.783、0.800、0.772和0.742、0.751、0.693、0.737、0.771。计算结果表明,对于顺倾向边坡,坡高对其稳定性影响最大,其次为弱面黏聚力和坡角,而弱面倾角和弱面内摩擦角相对影响较小；对于反倾向边坡,弱面内摩擦角对稳定性影响最大,其次依次为坡角、坡高、弱面黏聚力和弱面倾角。

4 结 论

a. 顺倾向边坡,当β≤15°时,其破坏形式主要是拉裂-剪切-滑移破坏,滑面不沿弱面;当15°<β<α时,产生顺层滑移破坏；β≥α时,坡顶沿弱面滑移,坡角弯折破坏。对于反倾向坡,β较小时为压剪型破坏,当β较大时为倾倒破坏。

b. 随着β的增大,顺倾向边坡的安全系数呈先减、后增、再减的趋势,且水平层状边坡的稳定性要高于直立边坡;而反倾向边坡的安全系数变化趋势与顺倾向边坡相反。当β>α时,顺倾向坡的稳定性要高于同倾角的反倾向坡。

c. 各因素对顺倾向和反倾向边坡的稳定性影响显著性不同。顺倾向边坡,坡高对其稳定性影响最大,其次为弱面黏聚力和坡角,而弱面倾角和弱面内摩擦角相对影响较小。对于反倾向边坡,弱面内摩擦角对稳定性影响最大,其次依次为坡角、坡高、弱面黏聚力和弱面倾角。

[ 1 ] 张玉军, 刘谊平.层状岩体的三维弹塑性有限元分析[J].岩石力学与工程学报, 2002, 21(11): 1615-1619.(ZHANG Yujun, LIU Yiping.3D elasto-plastic FEM analysis on layered rockmass[J].Chinese Journal of Rock Mechanics and Engineering, 2002, 21(11): 1615-1619.(in Chinese))

[ 2 ] 陈志坚,吉林.层状岩质边坡地下水分布特征及其控稳作用[J].河海大学学报(自然科学版),2001,29(1):107-110.(CHEN Zhijian,JI Lin.Distribution character and stability controlling effect of underground water in layered rock slope[J].Journal of Hohai University(Natural Sciences),2001,29(1):107-110.(in Chinese))

[ 3 ] 汪小刚,贾志欣,陈祖煜,等.岩质边坡倾倒破坏的稳定性分析方法[J].水利学报,1996,28(3):7-12.(WANG Xiaogang,JIA Zhixin,CHEN zuyu.The research of stability analysis of toppling failure of jointed rock slopes[J].Journal of Hydraulic Engineering, 1996,28(3):7-12.(in Chinese))

[ 4 ] 伍法权.云母石英片岩斜坡弯曲倾倒变形的理论分析[J].工程地质学报,1997,5(4):306-311.(WU Faquan.Theoretical analysis of bending and toppling deformation in slope ofmica-quartz schist[J].Journal of Engineering Geology,1997,5(4):306-311.(in Chinese))

[ 5 ] 刘小丽, 周德培.用弹性板理论分析顺层岩质边坡的失稳[J].岩土力学, 2002, 23(2): 162-165.(LIU Xiaoli, ZHOU Depei.Stability analysis of layered dip rocky slopes with elastic plane theory[J].Rock and Soil Mechanics, 2002, 23(2): 162-165.(in Chinese))

[ 6 ] 邓荣贵, 周德培, 李安洪, 等.顺层岩质边坡不稳定岩层临界长度分析[J].岩土工程学报, 2002, 24(2): 178-182.(DENG Ronggui, ZHOU Depei, LI Anhong, et al.On the critical length of unstable rock stratum on bedrock slope[J].Chinese Journal of Geotechnical Engineering,2002, 24(2): 178-182.(in Chinese))

[ 7 ] 朱晗迓, 马美玲, 尚岳全.顺倾向层状岩质边坡溃曲破坏分析[J].浙江大学学报(工学版), 2004, 38(9): 1144-1149.(ZHU Hanya, MA Meiling, SHANG Yuequan.Analysis of buckling failure of consequent rock slope[J].Journal of Zhejiang Universisty(Engineering Science), 2004, 38(9): 1144-1149.(in Chinese))

[ 8 ] 冯君, 周德培, 李安洪.顺层岩质边坡开挖模型试验及稳定性影响因素分析[J].工程地质学报, 2005, 13(3):294-299.(FENG Jun, ZHOU Depei, LI Anhong.Test and numerical modeling of the stability of rock bedded slope[J].Journal of Engineering Geology, 2005, 13(3):294-299.(in Chinese))

[ 9 ] 吴顺川, 金爱兵, 高永涛.基于遍布节理模型的边坡稳定性强度折减法分析[J].岩土力学, 2006, 27(4): 537-542.(WU Shunchuan, JIN Aibing, GAO Yongtao.Slope stability analysis by strength reduction method based on ubiquitous-joint model[J].Rock and Solid Mechanics,2006, 27(4): 537-542.(in Chinese))

[10] 蒋青青,胡毅夫,赖伟明.层状岩质边坡遍布节理模型的三维稳定性分析[J].岩土力学, 2009,30(3): 712-716.(JIANG Qingqing, HU Yifu, LAI Weiming.Three dimensional stability analysis of stratified rock slope based on ubiquitous-joint model[J].Rock and Soil Mechanics, 2009,30(3): 712-716.(in Chinese))

[11] 林杭,曹平,李江腾,等.层状岩质边坡破坏模式及稳定性的数值分析[J].岩土力学, 2010, 31(10): 3300-3304.(LIN Hang, CAO Ping, LI Jiangteng, et al.Numerical analysis of failure modes and stability of stratified rock slopes[J].Rock and Solid Mechanics, 2010, 31(10): 3300-3304.(in Chinese))

[12] 卢敦华,曲艳伟,何忠明,等.结构面强度参数对层状边坡稳定性影响的三维分析[J]中南大学学报(自然科学版),2011,42(1):147-151.(LU Dunhua,QU Yanwei,HE Zhongming,et al.Three dimensional analysis for effect of structural plane strength parameters on stratified slope stability[J].Journal of Central South University(Science and Technology), 2011,42(1):147-151.(in Chinese))

[13] 阎石,杜海涛,于琦乐,等.顺层岩质高边坡的静力稳定性安全评价[J].防灾减灾工程学报,2014,34(4):407-414.(YAN Shi,DU Haitao,YU Qile, et al.Static stability safety evaluation of high bedding rock slope[J].Journal of Disaster Prevention and Mitigation Engineering,2014,34(4):407-414.(in Chinese))

[14] Itasca Consulting Group.Inc.FLAC2D (fast lagrangian analysis of continua) Theory and Background[Z].Minneapolis:Itasca Consulting Group,2002.

[15] 张晓霞, 周柏卓.正交各向异性材料弹性本构关系分析[J].航空发动机, 1997, 23(1): 20-25.(ZHANG Xiaoxia,ZHOU Baizhuo.Elastic constitutive relation of orthotropic material[J].Aeroengine,1997,23 (1): 20-25.(in Chinese))

[16] 张鲁渝,郑颖人,赵尚毅,等.有限元强度折减系数法计算土坡稳定安全系数的精度研究[J].水利学报,2003,34(1):21-25.(ZHANG Luyu, ZHENG Yingren, ZHAO Shangyi,et al.The feasibility study of strength-reduction method with FEM for calculating safety factors of soil slope stability[J].Journal of Hydraulic Engineering,2003,34(1):21-25.(in Chinese))

[17] 邓聚龙.灰色系统基本方法[M].武汉:华中理工大学出版社, 1996.

Analysis of failure characteristics and stability of layered rock slope based on multi-fracture model of FLAC3D

LU Haifeng, YAO Duoxi, HU Youbiao, GUO Peng

(College of Earth and Environment, Anhui University of Science and Technology, Huainan 232001, China)

Using the FLAC3D multi-fracture constitutive relation, a numerical model of anisotropic failure characteristics of a layered rock slope was established. With the strength reduction method, the relationships between the slope safety coefficient and the interlayer weak plane dip angleβ, slope angleα, slope heightH, and shear strength of the rock mass were determined, and the impacts of various factors on the safety coefficient were investigated with the grey correlation method. Results show that for a bedding slope (with the slope direction consistent with the obliquity of the rock layer) atβ≤15°, damage is mainly caused by tensile cracking-shear-slippage failure, and a sliding surface does not occur along the interlayer weak plane; bedding slippage failure appears at 15°<β<α; and the top of the slope slips along the weak plane, and bending failure appears at the slope foot atβ≥α. For a reverse slope (with the slope direction opposite to the obliquity of the rock layer), the compression-shear failure is the main failure mode atβ<50°, and toppling failure appears whenβis larger (β≥50°). With the increase ofβ, the safety coefficient of the bedding slope shows a tendency to decrease first, then increase, and then decrease again, and the stability of the horizontal layered slope is higher than that of the vertical one. The safety factor change tendency of the reverse slope is opposite to that of the bedding slope. In the case ofβ>α, the stability of the bedding slope is higher than that of the reverse slope at the same dip angle. For a bedding slope, the slope height has the greatest impact on the stability, followed by the cohesion of the weak plane and slope angle, and the influences of the dip angle and friction angle of the weak plane are relatively small; for a reverse slope, the influence of each factor on its stability is ranked by the friction angle of the weak plane, slope angle, slope height, and cohesion and dip angle of the weak plane.

multi-fracture model; layered rock slope; stability; strength reduction

国家自然科学基金(51474008,41472235);安徽省自然科学基金(1508085QE89)

鲁海峰(1983—),男,副教授,博士,主要从事岩石力学与地质灾害研究。E-mail:luhaifeng7571@126.com

10.3880/j.issn.1006-7647.2017.04.007

TU457

A

1006-7647(2017)04-0036-06

2016-07-20 编辑：郑孝宇)