论流域水文模型

芮孝芳

(河海大学水文水资源学院，江苏 南京 210098)



论流域水文模型

芮孝芳

(河海大学水文水资源学院，江苏 南京 210098)

论述了流域水文模型结构和参数的水文学基础、物理上的耦合关系，以及集总式流域水文模型与分布式流域水文模型的本质区别，讨论了2种模型解算方法的特点，以及在参数率定中产生异参同效的原因和减少异参同效影响的措施；提出了一个比较客观的模型验证和相互比较的方法。

流域水文模型；集总式模型；分布式模型；异参同效；大数据

早在20世纪60年代后期，流域水文模型一经问世，水文学术界就抱有2种截然不同的态度：一是认为有了“模型”就可以由降雨过程直接推算出洪水过程了，水文观测将来就不再需要了；二是认为“模型”就是传统上所说的“公式”，并不因为将“公式”换成“模型”就能解决实际中遇到的复杂水文问题。持前一种态度者显然表现出了对新事物的盲目性，而持后一种态度者则似乎还未意识到“模型”的潜在作用。半个世纪过去了，人们对流域水文模型的认识和理解已渐渐走向理性，对“模型”无论是“夸张”或“保守”的看法，都是缺乏严肃科学性的表现。

世界上第一台电子计算机1945年在美国Pennsylvania大学诞生，世界上第一个真正意义上的流域水文模型——Stanford模型1966年在美国Stanford大学诞生。这2件事先后都发生在美国，凑巧体现了流域水文模型是水文学与计算机科学相结合的产物。流域水文模型的兴起标志有着300多年发展史的定量水文学通过接受现代科学技术的渗透，在经历了缓慢发展阶段后开始进入快速发展阶段。流域水文模型为考虑流域降雨径流形成的精细机理和复杂的耦合关系提供了新的研究工具。

笔者从事水文学研究已逾半个世纪，不仅亲身感受到流域水文模型从“黑箱子”“概念性”向“具有物理基础”，从集总式、分散式向分布式，从仅考虑确定性向同时考虑确定性和不确定性，从仅模拟降雨径流形成过程向耦合模拟泥沙、水质过程的如火如荼发展历程，而且目睹了流域水文模型表面繁荣以及存在的阻碍其进一步发展的深层次问题，近年更是无时无刻不在思索这些问题。现将对这些问题的所思所想归纳成模型的结构及参数、集总式模型和分布式模型、模型的解算、不敏感参数和异参同效、模型的验证和比较等5个问题，在本文中展开讨论。

1 模型的结构及参数

通过一定的结构及参数模拟流域上一场特定时空分布降雨形成的流域出口断面流量过程是研究流域水文模型的目的。水文学已经揭示，流域降雨径流形成将经历2种机制[1]:其一为降雨量再分配机制，结果导致降雨量分成损失量和净雨量两部分，净雨量可形成地面径流、壤中水径流、地下水径流等径流成分；其二为净雨过程再分配机制，结果导致净雨过程推移和坦化成流域出口断面流量过程，流域对净雨过程的推移和坦化作用综合起来就是流域调蓄作用。前一个再分配发生在包气带，是流域产流问题；后一个再分配发生在坡面、相对不透水面、含水层、河网等场合，是流域汇流问题。产流问题涉及截留、填洼、下渗、蒸散发、土壤水分变化等过程，汇流问题则涉及净雨量从坡面上、土壤中和河网内向流域出口断面的汇集过程。因此，流域水文模型的结构和参数必须具有处理流域产流和流域汇流的功能，如图1所示，在数学上可表示为

Q(t)=ψ(x1(t),x2(t),…,

xn(t),b1,b2,…,bn)

(1)

式中：x1(t)、x2(t)、…、xn(t)分别为流域空间位置1、2、…、n处的降雨过程与雨期蒸散发过程的差值，即为流域水文模型的输入；b1、b2、…、bn为相应的初始条件；Q(t)为x1(t)、x2(t)、…、xn(t)在流域下垫面作用下形成的流域出口断面流量过程，即为流域水文模型的输出；ψ为流域水文模型的结构及参数，起着流域下垫面对x1(t)、x2(t)、…、xn(t)的上述2种再分配作用。式(1)也可表达为

Q(t)=φ(x1(t),θ1,b1；x2(t),θ2,b2；

…;xn(t),θn,bn)

(2)

式中：θ1、θ2、…、θn分别为流域空间位置1、2、…、n处下垫面对x1(t)、x2(t)、…、xn(t)作用的参数；φ为流域水文模型的结构；其余符号意义同前。

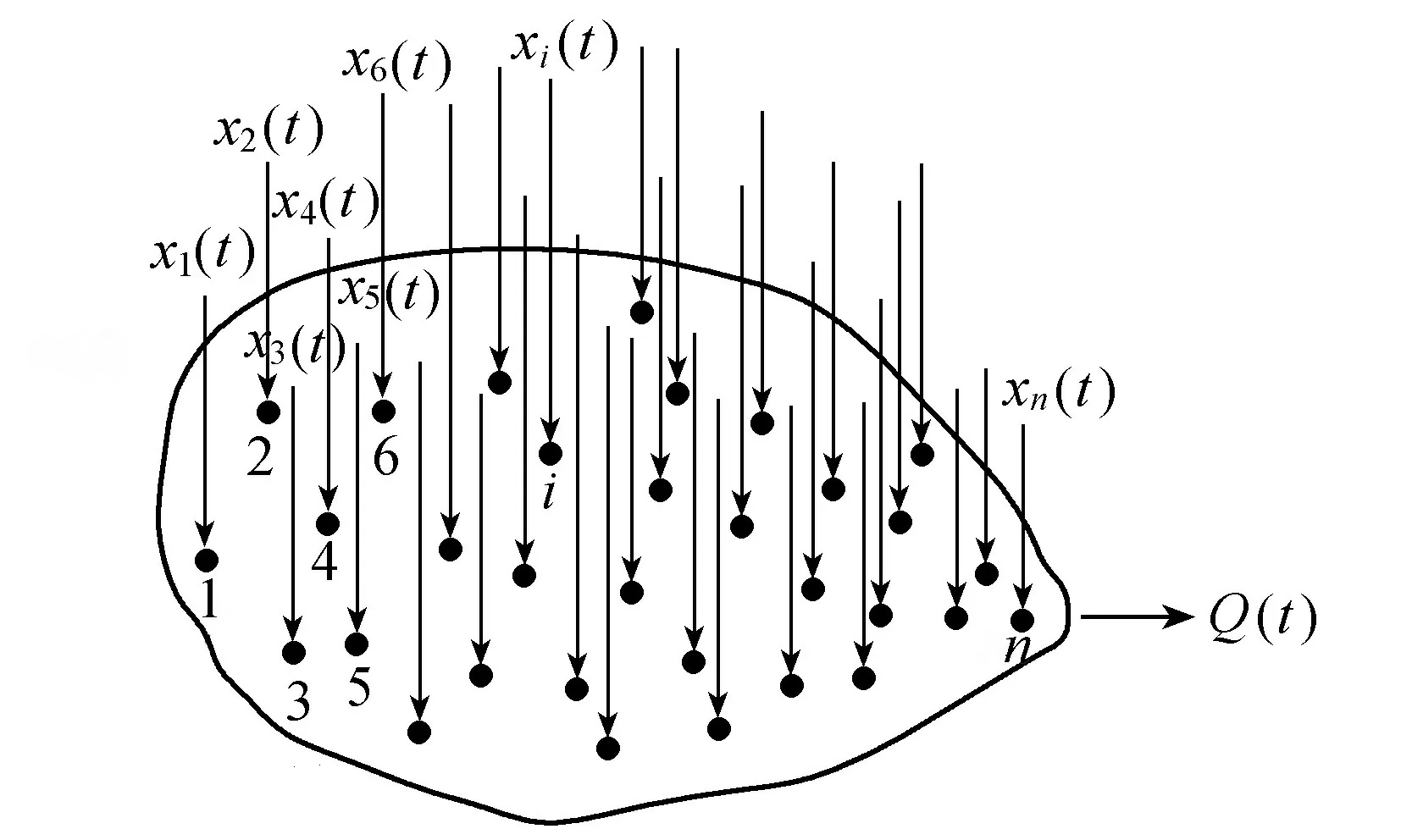
图1 一场降雨形成的流域出口断面流量过程

式(1)和式(2)表明，流域降雨径流形成是一个必须用多输入单输出系统描写的水文现象(图1)，不仅如此，而且其中每个输入在形成相应的输出时经历的下垫面作用有所不同，它们合成总输出的机理也可能十分复杂。理论上式(1)和式(2)中的n应为无穷大，但为了实用n只能取有限值，对此有2种处理方法:一是将流域剖分成若干个单元；二是假设降雨、蒸散发、初始条件和下垫面作用均为空间分布均匀，即x1(t)=x2(t)=…=xn(t)=x(t),θ1=θ2=…=θn=θ,b1=b2=…=bn=b。对于后一种处理方法，式(1)和式(2)分别简化为

Q(t)=ψ(x(t)，b)

(3)

Q(t)=φ(x(t),θ,b)

(4)

此外，在流域降雨径流形成过程中，若存在输出对下垫面的反馈作用，则式(4)应改为

Q(t)=φ(x(t),θ(Q),b)

(5)

式中θ(Q)为Q(t)函数的参数组。式(5)显然比式(4)复杂得多，但在一般情况下输出对下垫面的反馈作用并不明显。

由此可知，流域水文模型是通过结构与参数的耦合来达到模拟流域降雨径流形成的物理图景的目的的。参数用来描写下垫面对模型输入的作用，其中产流参数描写下垫面的透水性、热性质、缺水程度等对模拟输入的作用，汇流参数描写下垫面的地形、粗糙度、大小形状、水系分布等对模型输入的作用。而结构所体现的则是模型的输入和参数与模型输出之间的物理关系。结构与参数都是流域水文模型的核心问题，两者必定相依存在。因此，将流域水文模型简单地说成“结构+参数”容易引起误导。曾经有一种说法：参数是模型的关键，只要参数合理、正确，结构简单的模型也可以获得比结构复杂的模型好的模拟结果。这种说法貌似有理，其实有害。因为结构不合理的模型，其中参数是不可能有清晰的物理意义，并予以正确定量的。结构与参数两者的正确性是相辅相成的，只有流域水文模型的结构正确，其中的参数才可能有清晰的物理意义，其定量才可能合理、正确，模拟结果才可能与现实世界的物理图景一致。将流域水文模型参数视作随模型输入而变也是误导，因为流域出口断面流量过程是下垫面对输入作用的结果，所以模型中的参数仅反映下垫面对模型输入的作用，而不是参数受到输入的影响。人类活动对流域产汇流的影响，一般是通过改变下垫面来影响模型参数的，也不能认为是参数受到了输入的影响。流域水文模型参数本质上是反映下垫面对模型输入作用的物理量，必然与流域下垫面特征有密切的关系，可以依据普适性物理定律和水文现象本构关系，通过科学实验、理论推导、统计综合等研究方法揭示这种关系[2]。可以设想，随着这种定量关系的不断被揭示，依赖实测水文资料，利用最优化算法率定的流域水文模型参数将会逐步减少。

2 集总式模型和分布式模型

早期的流域水文模型，限于当时对流域产汇流机理的认识水平，几乎都是集总式的，即模型的结构和参数都是针对整个流域的，模型的输入要么必须空间分布均匀，要么视作集中式单输入，其数学表达式为式(4)。后来发现，这种集总式的流域水文模型，由于忽略了下垫面条件空间变异性和输入空间分布及其不均匀对流域产汇流的影响，因此，即使求得的流域出口断面流量过程与实测结果吻合很好，也不能证明模型的结构和参数是正确的[3]。

有鉴于此，一些水文学家开始寻求对集总式流域水文模型的改进，例如Stanford模型[4]用下渗能力面积分配曲线考虑下垫面空间变异对超渗地面径流的影响；新安江模型[5]用流域蓄水容量曲线考虑下垫面空间变异对蓄满产流总径流的影响。由于下渗能力面积分配曲线和流域蓄水容量曲线均为统计曲线，只有统计意义，因此，这类流域水文模型只能考虑降雨空间分布均匀时下垫面空间变异对流域产流的影响，而不能同时考虑降雨空间分布不均匀和下垫面变异对流域产流的影响，也不能考虑作为多输入的净雨，在其空间分布不均匀时对流域汇流的影响。为区别于集总式流域水文模型，称这类流域水文模型为半分布式流域水文模型。

为了使半分布式流域水文模型能进一步考虑降雨空间分布不均匀对流域产汇流的影响，水文学家提出按流域中雨量站布局将流域划分成不嵌套、数目与雨量站数目相当的子流域，使每个子流域降雨空间分布基本均匀。对这样的子流域，显然可使用半分布式流域水文模型来考虑子流域下垫面变异对其产流的影响，若再通过河网汇流，就可将各子流域的输出汇集成流域出口断面流量过程。这样就得到了分散式流域水文模型。与半分布式流域水文模型相比，分散式流域水文模型仅仅是一个初步考虑降雨空间分布不均匀对流域产流影响的模型。由于受到雨量站密度的制约，难以保证每个子流域的降雨空间分布基本均匀，加之描述下垫面空间变异的下渗能力面积分配曲线和流域蓄水容量曲线是统计曲线，它不仅未解决好降雨空间分布不均对流域产流的影响，而且仍未能解决净雨空间分布不均匀对流域汇流的影响。

经历一段曲折的发展过程后，分布式流域水文模型终于来到了这个世界[6]，与集总式、半分布式和分散式流域水文模型不同，分布式流域水文模型必须能同时考虑降雨空间分布及其不均，以及下垫面空间变异对流域产汇流的影响。因为分布式流域水文模型的最主要特征是需要对流域进行剖分，也就是必须将流域划分成许多互不嵌套也不交叉、能够支撑精细描述降雨空间分布和下垫面变异的小单元。每个单元内的下垫面将基本一致，降雨空间分布亦均匀，而不同单元的下垫面和降雨量则可以相同，也可以不同。对流域通过这样的处理，模型的降雨输入就是多输入、分布式，而不是单输入、集总式，模型的参数也是分布式而不是集总式，其数学表达式为式(2)。建立在对流域进行剖分基础上的分布式流域水文模型，不仅能同时考虑降雨空间分布不同和下垫面变异对流域产流的影响，而且能考虑由此造成的净雨空间分布不均对流域汇流的影响，其模拟的精度将取决于模型结构物理上的合理性、参数的正确性、单元的尺寸、单元之间产汇流联系等。

虽然分布式流域水文模型的主要表征是必须对流域进行分剖分，但这并等于只要对流域进行剖分就算是分布式流域水文模型了，将流域划分成许多不嵌套也不交叉、能够支撑精细描述降雨空间分布和下垫面变异的小单元只是分布式流域水文模型的必要前提，而不是充分条件。有些所谓分布式流域水文模型只是将流域进行了网格化，不仅仍使用流域平均降雨以单输入形式作为模型输入，而且每个网格单元的模型参数也仍采用完全相同的值，这种不是实质性考虑降雨空间分布及其不均匀和下垫面变异对流域产汇流影响的流域水文模型，并不是真正的分布式流域水文模型。

分布式流域水文模型要求将流域剖分，与求微分方程数值解要求将流域划分成网格或有限单元不是同一个概念，前者是为了考虑降雨空间分布及其不均匀和下垫面变异对流域产汇流的影响，而后者则是为了利用有限差分或有限单元将微分方程转换成代数方程来求解。笔者认为只有流域产汇流能用一组数学物理方程描写并用有限差分法或有限单元法进行数值求解的特殊情况，流域剖分才是“一箭双雕”，除此而外将两者混为一谈是不合适的。

流域水文模型从集总式向分布式的发展，标志着水文科学正逐步走向成熟，世界科技正逐步走向高端。因为如果没有产汇流理论的长足进步和计算机技术、GIS技术、遥感技术等的有力支撑，分布式水文模型的研制及应用都将是十分困难的。

3 模型的解算

在流域水文模型的结构和参数已确定的前提下，根据其输入推求其输出即为模型的解算。流域水文模型的结构可能是一组微分方程，也可能是数学表达式与逻辑关系的集成。如果用连续介质力学观点考察流域产汇流过程，模型结构将由微分方程组和相应定解条件构成的定解问题来表达[7]。如果用水文学观点考察流域产汇流过程，由于“界面效应”“门槛效应”“调蓄效应”等可以描述流域产汇流现象[1]，模型结构就可用集成这些“效应”的数学式与逻辑关系来表达。

SHE模型是迄今为止唯一一个全部用连续性方程和动力方程控制流域产汇流的流域水文模型[7]。由描述流域产汇流各子过程的连续性方程和动力方程构成的方程组本质上是一个具有耦合关系的非线性偏微分方程组，再加上复杂的定解条件，就成为至今无法得到解析解的复杂数学问题。SHE模型选择了数值解，即利用有限差分格式将偏微分方程组离散成代数方程进行数值求解。SHE模型曾用于模拟英国威尔士的Wye河流域的产汇流过程。Wye河流域是一个面积仅为10.55 km2的小流域，平面网格的尺度采用250 m×250 m,包气带垂向划分成38个子层，每个子层的土厚为0.05 m。耗费了大量人力和时间，虽获得了计算结果，但精度令人失望。SHE模型将流域网格化原本是为了微分方程的数值解，但事实上也适应了模型考虑降雨空间分布和下垫面空间变异对流域产汇流影响的需要，因此是一个分布式流域水文模型。

模型解算的另一种思路是先给出流域产汇流过程所包含的每个子过程的解，然后将这些子过程的解按其在流域产汇流过程中物理上的关联进行集成，最终形成模型的解，这样就避开了对复杂的非线性微分方程组的求解。现以新安江模型为例[5]具体说明这种模型解算的思路。新安江模型先将流域产汇流过程分成流域产流和流域汇流2个阶段。在流域产流阶段，用三层蒸散发模式推求不同时刻的流域蒸散发量，以包气带蓄水容量为“门槛”确定蓄满产流总径流量，用流域蓄水容量曲线考虑降雨空间分布均匀时包气带蓄水容量空间变异对流域产流的影响，以带底孔和侧孔的“线性水库”将总径流量划分成饱和地面径流、壤中水径流、地下水径流等径流成分。在流域汇流阶段，用单位线或等流时线或线性水库串并联结构分析坡面汇流、壤中水汇流和地下水汇流，用水文学洪水演算法或水力学洪水演算法分析河网汇流。容易理解，新安江模型的这种解算思路并不因流域尺度而不同，因此，这种思路如针对整个流域，就成为集总式流域水文模型的解算思路；如针对子流域和单元，再考虑各子流域或各单元的水流汇集关系，就成为分散式流域水文模型和分布式流域水文模型的解算思路。

与SHE模型相比，新安江模型的解算思路具有3个特点：一是用“界面效应”“门槛效应”“调蓄效应”等代替控制连续介质运动的微分方程组；二是对于一些子过程之间的耦合关系，利用分单元、分阶段、分径流成分、分先后次序等思路，通过有关参数或系数进行解耦，避开了复杂的微分方程组的求解；三是用线性理论处理模型解算中遇到的“分解”和“聚合”问题，忽略非线性干扰。

相当长时间以来，一般认为上述前一种模型解算思路才是具有物理基础的，其实后一种模型解算思路的物理意义也是明确的。对于前一种模型解算思路，由于流域产汇流的每个子过程并非均属于连续介质运动，加之数学求解的困难，要达到实用的目的看来还有很长的路要走。对于后一种模型解算思路，由于在保持基本物理概念的前提下避开了复杂的数学处理，是仍有发展空间的模型解算思路。受“大数据”的启发[8]，笔者曾提出模型解算的新思路，具体可参见文献[9-10]。

4 不敏感参数和异参同效

流域水文模型包含的参数，一般分为3类：一是几何参数；二是物理参数；三是经验参数。经验参数指无明确几何意义和物理意义的参数，无法直接测定，也无法由理论导出。几何参数和物理参数中也会有一些直接测定困难甚至不可能者，这些参数只能通过有关实测资料反求，称这种确定模型参数的方法为“率定”。率定的准则一般是模拟与实测结果的吻合程度，反映这种吻合程度的指标可用计算误差，也可用确定性系数。用计算误差作指标，则误差越小，吻合程度越高；用确定性系数作指标，则确定性系数越大，吻合程度越高。

参数率定在数学上是一个最优化问题，它由目标函数和约束条件构成。能使目标函数在约束条件制约下达到极小或极大的参数值就是采用的模型参数值。目标函数可基于计算误差来构建，也可基于确定性系数来构建，但基于相关系数构建目标函数是不妥的，因为相关系数只能说明模拟值与实测值的相关程度，用以说明模拟值与实测值的吻合程度是不充分的。

就参数率定方法的技术思路本身而言，至少可能有2个问题会影响到所得模型参数的客观、合理性：一是不敏感参数的存在；二是异参同效的干扰。因此，在模型参数率定时识别不敏感参数，回避异参同效就显得十分重要。

Beven等[11]提出的GLUE(generalihood uncertainty estimation)法就是一个识别不敏感参数的方法。GLUE法基于Monte-Carlo统计试验的思路，先在待率定参数可能的取值范围内随机抽取数量庞大的参数组，如果模型包含有n个待率定参数，那么每个参数组就是n维空间中一个点，对每个参数组驱动模型即可得相应的目标函数值，然后点绘参数组中每个参数与相应的目标函数值的散点图(图2)。这种散点图表明，对应于参数组中任一参数的一定取值，将有其他参数的随机取值与之构成不同的参数组，并可得出相应的目标函数值，其中可能有一个极值，这样的极值是随该参数的取值而变化的，其连线就是散点图的外包线(图2)。如果散点分布如图2(a)所示，那么说明参数组中的参数θj是不敏感参数，因为对不同的θj，当与其他参数配合时得到的目标函数极值相同或几乎相同。如果散点分布如图2(b)所示,那么说明参数组中的参数θj是敏感参数，因为对不同的θj，当与其他参数配合时得到的目标函数极值不同，而且峰值明显或最大峰值明显。曾经有人将GLUE法按字面理解成是识别不确定性的方法，笔者认为这容易引起混淆，因为率定模型参数出现解的不确定性就是解的不唯一性，这与自然现象表现为不确定性并非同源。在理解了异参同效问题后还会明白，其实GLUE法只是一个识别不敏感参数造成异参同效的方法。将不敏感参数识别出来后，应当根据其物理意义和有关经验先予确定，使其不再参与参数率定，以免由此引起异参同效问题。

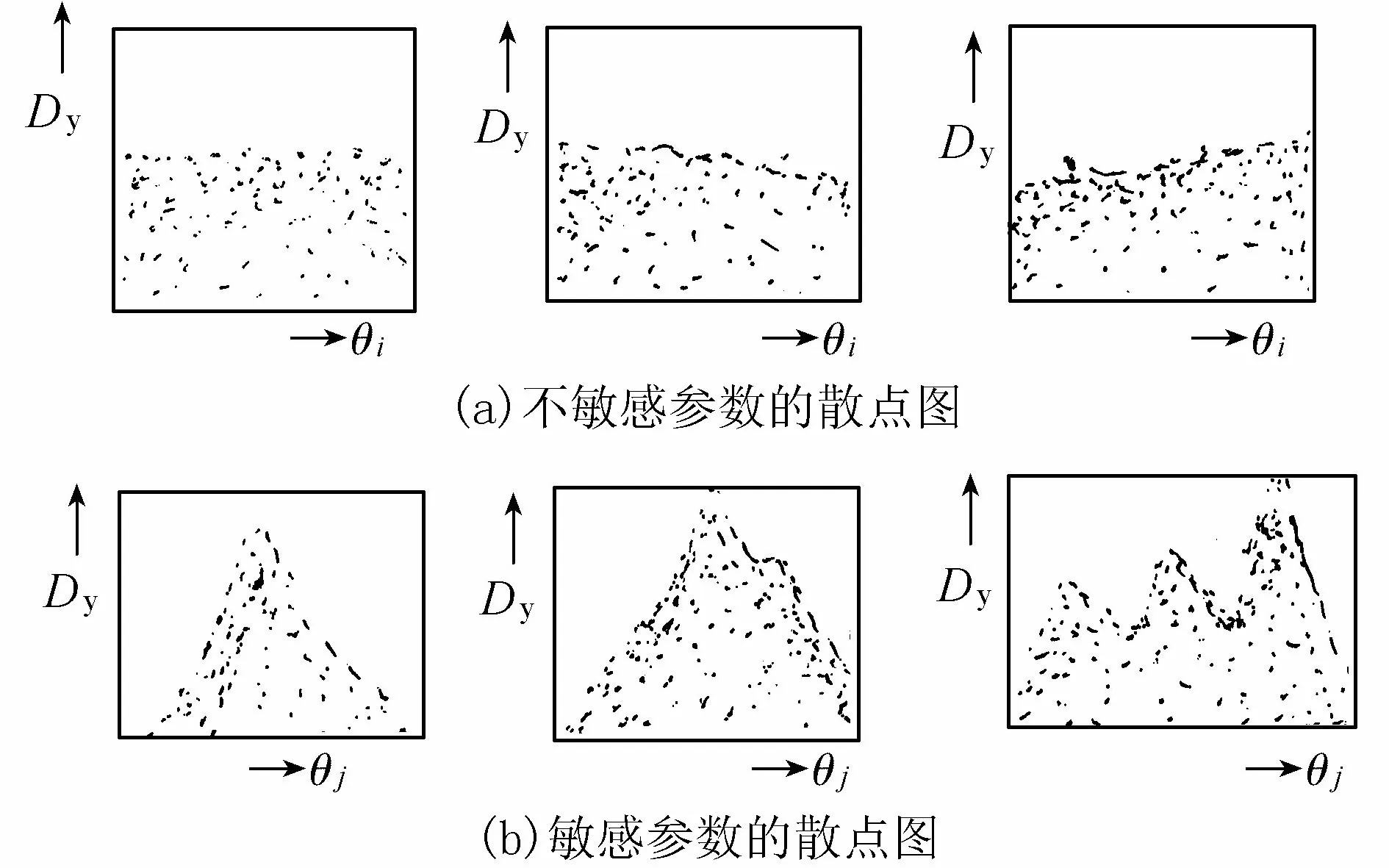
图2 模型参数θj与确定性系数Dy的散点图

如果模型只包含一个待率定的敏感参数，那么只要目标函数存在极值，就一定能通过率定获得该敏感参数的唯一解，即不存在异参同效问题。但是，如果模型包含2个待率定的敏感参数，情况就要复杂一些。这时，即使目标函数存在极值，也不一定能获得这2个待率定敏感参数的唯一一组解，即可能出现异参同效问题。应用响应面可以直观地识别只有2个待率定敏感参数的模型是否存在异参同效问题。因为目标函数值与2个待率定参数之间的关系可视为三维空间中的“几何体”，其在平面上的投影将是以目标函数值为参变量的2个待率定参数的关系即响应面(图3)。若响应面近似同心圆(图3(a))，则必然有一组敏感参数能使目标函数达到极值，表明解是唯一的，不存在异参同效问题；若响应面为一系列不相交的狭长椭圆(图3(b))，则由于与目标函数极值相应的敏感参数组有无穷多，解不唯一，因而必然存在异参同效问题。图3(c)和图3(d)所示为目标函数具有多极值的情况，其中图3(c)为每个极值相同的多极值情况，表明有有限组敏感参数能使目标函数达到同样的极值，仍属于存在异参同效问题的情况，而图3(d)为每个极值不相同的多极值情况，表明必有一组敏感参数能使目标函数达到极值中的极值，因而可归入不存在异参同效之列。当模型包含的待率定敏感参数多于2个时，上述识别异参同效问题的方法仍可使用，只要先将待率定敏感参数分成不重复的两两一组就可以了。不难看出，若模型包含的待率定敏感参数较多，识别其异参同效问题将是一件很烦琐的事。

具有多于2个敏感参数的流域水文模型，用最优化方法率定参数之所以有可能出现异参同效问题，数学上是因为所采用的最优化算法未能形成与待定敏感参数相同数目的方程，以致实际上是在解一个没有唯一解的不定方程组；而物理上则是因为敏感参数之间存在相互补偿作用，即所谓互补性。例如在新安江模型中，控制蓄满产流流域产流量的敏感参数是流域蒸散发系数K和流域蓄水容量Wm。对于一个流域，降雨量形成径流量是一个客观的水文过程，但如果通过调试K和Wm来模拟这个水文过程，就会发现有多组K和Wm值都是合适的，因为当降雨相同时，取大一些的K及小一些的Wm值，或取小一些的K及大一些的Wm值，存在相互补偿，因而将会取得基本一致的模拟结果。流域水文模型中一些敏感参数对模拟结果所表现出的这种相互补偿作用，表面上似乎是它们之间“相关性”的体现，但却不能理解为参数之间存在什么相关关系，事实上，也许它们在物理上没有任何联系，就像新安江模型中的流域蒸散发系数K和流域蓄水容量Wm没有任何物理联系一样。因此，在这里是不宜用“相关性”代替“互补性”的。

如果说敏感参数之间的互补性是产生异参同效的内因，那么各种误差的存在就成为加重异参同效的外因。用最优化方法率定模型的敏感参数，误差主要来自以下几方面：一是降雨和流量观测误差；二是处理降雨空间分布的误差；三是模型结构不合理误差；四是最优化方法构建不完善误差；五是数值计算的截断和舍入误差；六是确定初始条件的误差。利用理想资料可以揭示前3种误差对异参同效的影响。所谓理想资料就是由已知结构和参数的流域水文模型在确定的初始条件下生成的资料，由于这种理想资料没有降雨和流量观测误差、处理降雨空间分布的误差、确定初始条件的误差和模型结构不合理误差，因此，通过比较可以得知仅仅是敏感参数的互补性对异参同效的影响。另外2种误差，即最优化方法构建不完善误差和数值计算的截断和舍入误差对异参同效的影响，也可以针对理想资料，通过使用不同的目标函数和不同的最优化算法获得的结果比较得知，具体请参阅文献[12-13]。

异参同效无疑是流域水文模型研制和应用的“天敌”。因此，尽可能消除异参同效的影响是流域水文模型发展中必须解决的瓶颈问题[14]。笔者初步认为，克服异参同效问题的思路和措施主要是：尽可能通过实验或理论提高模型结构的精度并独立给出模型参数的物理定量方法或合理取值范围；识别出不敏感参数，使其不要混杂在待率定的参数之中；将流域水文模型合理地分解为一些子模型，分别制定相应的目标函数，以减少每个目标函数所包含的待率定参数；借助高新技术手段，提高降雨和流量观测以及处理降雨空间分布的精度；选择合适的目标函数形式和最优化算法等。

5 模型的验证和比较

对流域水文模型进行验证的重要性是不言而喻的，但笔者从现有诸多文献中发现，对待这个问题确实存在一些值得商榷的做法，例如：有的片面地以与实测流量过程线拟合最优作为准则；有的以少许几场洪水甚至一场洪水拟合合格论“英雄”；有的仍使用参与率定模型的那些资料作为验证资料；有的甚至改用洪水历时曲线而不用洪水过程线进行验证等。在模型验证阶段最应该防止的就是那些伪证，而上述这些做法均存在作伪证的风险。

鉴于水文学理论至今还未成熟到能完全从物理上揭示流域产汇流机理和规律的程度，水文观测资料误差的不确定性也不可避免，因此，验证模型的充分客观方法是缺失的。作为一孔之见，笔者在总结以往经验的基础上，试图提出下列一些原则性建议，作为进行模型验证的参考：一是判断所选用的流域水文模型的结构是否适合研究流域的产汇流机理，如发现有不适合的地方，应对模型结构作适当改进，或者重新选用或研制更适用的模型，不要盲目套用；二是对降雨径流观测资料和其他相关信息的可靠性要进行认真审核，对雨量站网能否较好地控制降雨空分布不均匀性要进行科学评估；三是用作率定模型参数的那组资料不得再用作验证，但可以互相交换，实行“往返”验证(“往返”验证的去伪存真作用一般会比“单向”验证明显)；四是无论是率定模型参数，还是验证模型结构，都不能只取1场或2场洪水，一般应取5～10场洪水，而且能跨越3～5年；五是充分利用径流实验站的观测资料，甚至室内水文实验成果进行模型验证。

现在全世界已有数以百计的流域水文模型[15]，每个模型的产生都有其一定的物理背景或应用需求。由于水文学还不能完全准确揭示流域产汇流机理和规律，因此不同模型之间存在差异是难以避免的，于是，模型比较研究就摆到了水文学家的面前，世界气象组织(WMO)[16]曾于1967年组织了一次世界性的流域水文模型“竞赛”，竞赛的规则简单而直观，竞赛前匿名公布一些流域的部分实测水文资料及流域地形、地貌、气候、水利工程等基本信息，供参赛者率定和验证模型参数之用，竞赛时再公布这些流域的另一部分实测水文资料，供参赛者在比赛现场验证模型之用。竞赛的评判准则就是现场验证精度。中国于1997年也举办过类似的流域水文模型“竞赛”[17]。笔者认为，这种不顾及模型结构与参数是否科学地反映研究流域的产汇流特点，仅以拟合精度作为唯一指标的模型比较是有一定缺陷的。因为不同模型的差异首先体现在其结构和参数上，因此，在进行模型比较时，必须将结构和参数的比较放在重要位置，应当从水文学原理上搞清楚参与比较的模型模拟流域产汇流特性的差别，再利用理想资料定量分析这些差异所引起的结果。对于后者，具体步骤如下所述。

令待比较的2个流域水文模型为A和B，先利用其中一个模型，例如模型A，生成理想资料，这样生成的理想资料显然是完全符合模型A的结构和参数的。再将这样的理想资料分成两部分，其中一部分用于率定模型B的参数，另一部分则用于验证模型B。如果验证精度令人满意，那么就可认为模型B和模型A所描述的流域产汇流特点相近，2个模型的模拟精度接近，在实际应用中可认为是适用性基本相同的2个流域水文模型；反之，就可认为这2个模型所描述的流域产汇流特点相差较远，模拟精度大相径庭，在实际应用中是适用性有很大差异的2个流域水文模型。为了增加这种比较分析的客观性，一般尚须将2个被比较的模型互换后再进行一次比较。

实验和逻辑是科学研究的两大基石[18]。前者为德国哲学家培根提出，他认为凡是不能用实验证明的命题，都值得怀疑；后者为法国科学家笛卡尔提出，他认为凡是不能用从最基本前提出发演绎证明的命题，都值得怀疑。现实情况是，在流域水文模型的验证和比较中，实验验证十分缺乏，演绎证明残缺不全。流域水文模型的发展举步维艰，这是值得每一个水文学家深思的问题。

6 结 语

流域水文模型的结构和参数必须尽可能反映流域的产汇流特点，这样才有可能使模拟结果与实际发生的现象有好的物理上的吻合。模型结构描写的是模型输出与输入、初始条件和参数之间的函数关系，模型参数体现的是模型输入在下垫面作用下将怎样形成模型输出的。

由于降雨呈空间分布及其不均匀性，以及下垫面空间变异，构建能考虑这些因素对流域产汇流影响的流域水文模型是水文学家追求的目标。分布式流域水文模型因此受到水文学家的青睐，而对流域产汇流真实物理机理作了概化和均化的集总式流域水文模型，虽然能模拟出与出口断面流量过程比较一致的结果，但并不能表明其结构和参数在物理上是合理的。集总式流域水文模型本质是一种基于均化思想的模型，它不能反映水文现象的真实物理过程；分布式流域水文模型则是基于精细化思想的模型，理论上应能反映水文现象的真实物理过程。

将流域产汇流视作连续介质运动，用所导出的一组偏微分方程及一组定解条件来表达分布式流域水文模型的结构参数，不仅基本假定的合理性有待验证，而且数学求解十分困难，至今尚无比较成功的算例。而基于流域剖分、“界面效应”“门槛效应”和“调蓄效应”等概念构建的分布式流域水文模型，无论模型的表达还是数学求解都比较容易实现。

只要模型中包含2个以上的敏感参数，用最优化方法率定模型就有可能发生异参同效问题。当消除模型中不敏感参数干扰后，之所以发生异参同效问题，内因是参数之间的补偿作用，外因是资料误差、结构不合理、初始条件误差、目标函数形式，以及数值计算的截断和舍入误差。现在的问题主要不是去发现异参同效的存在，而是要努力去寻找减少甚至消除异参同效的良策。

模型验证是消除其结构和参数虚假性，增加其合理、可靠性的重要措施之一，仅以模拟值与实测值吻合作为验证准则可能有失客观性，采用“往返”验证是一个现实可行的方法。模型比较也不能只以拟合精度为唯一准则，必须尽可能对模型结构和参数作物理上的比较分析。在此前提下，采用理想资料再作定量分析是有意义的。

务必牢记，模型是用来解决问题的，不是用来当花瓶作摆设的。

[ 1 ] 芮孝芳.水文学原理[M].北京：高等教育出版社，2013.

[ 2 ] 芮孝芳，蒋成煜.流域水文与地貌特征关系研究的回顾与展望[J].水科学进展，2010，21(4)：444-449.(RUI Xiaofang,JIANG Chengyu.Review of research of hydro-geomorphological processes interation[J].Advances in Water Science,2010,21(4):444-449.(in Chinese))

[ 3 ] 芮孝芳.流域水文模型研究中的若干问题[J].水科学进展，1997，8(1)：94-98.(RUI Xiaofang.Some problems in research of watershed hydrological model[J].Advances in Water Science,1997,8(1):94-98.(in Chinese))

[ 4 ] CRAWFORD N H,LINSLEY R K.Digital simulationin hydrology:Stanford Watershed Model Ⅳ[R].Palo Alto,CA:Stanford University,1966.

[ 5 ] 赵人俊.流域水文模拟：新安江模型与陕北模型[M].北京：水利电力出版社，1984.

[ 6 ] 芮孝芳，黄国如.分布式水文模型的现状与未来[J].水利水电科技进展，2004，24(2)：55-58.(RUI Xiaofang,HUANG Guoru.Today and future of distributed hydrologic models[J].Advances in Science and Technology of Water Resources,2004,24(2):55-58.(in Chinese))

[ 7 ] ABBOTT M B,BATHURST J C,CUNGE R E,et al.An introduction to the European Hydrological System-Systeme Hydrologique Europeen,“SHE”,1:history and philsophy of a physically based distributed modelling system[J].Journol of Hydrology,1986,87:45-59.

[ 8 ] 芮孝芳.水文学与“大数据”[J].水利水电科技进展，2016，36(3)：1-4.(RUI Xiaofang.Hydrology and big data[J].Advances in Science and Technology of Water Resources,2016,36(3):1-4.(in Chinese))

[ 9 ] 芮孝芳.随机产汇流理论[J].水利水电科技进展，2016，36(5)：8-12.(RUI Xiaofang.Random theory of runoff yield and flow concentration[J].Advances in Science and Technology of Water Resources,2016，36(5)：8-12.(in Chinese))[10] 芮孝芳.单元嵌套网格产汇流理论[J].水利水电科技进展，2017，37(2)：1-6.(RUI Xiaofang.Theory of runoff yield and confluence by grid inlaid in watershed basic unit[J].Advances in Science and Technology of Water Resources,2017，37(2)：1-6.(in Chinese))

[11] BEVEN K J,FREER J.Equifinality,data assimilation,and uncertainty in mechanistic modeling of complex environmental systems using the GLUE methodolgy[J].Journal of Hydrology,2001,249:11-29.

[12] 张超.流域水文模型参数自动优化率定及不确定性研究[D].南京：河海大学，2010.

[13] 朱君君.Nash模型异参同效问题及参数确定方法研究[D].南京：河海大学，2011.

[14] 芮孝芳.水文学前沿科学问题之我见[J].水利水电科技进展，2015，35(5)：95-102.(RUI Xiaofang.Discussion of some frontier problems in hydrology[J].Advances in Science and Technology of Water Resources,2015，35(5)：95-102.(in Chinese))

[15] SINGH V P,WOOLHISER D A.Mathematical modeling of watershed hydrology[J].Journal of Hydrologic Engineering,2002,7(4):270-292.

[16] WMO.Intercomparison of conceptual models used in operational hydrological frecasting[R].Gneve,Switzerland:WMO Operational Hydrology,1975.

[17] 全国水文预报技术竞赛水文预报技术组.流域水文模型精度验证及进一步发展模型的建议[J].水文，1999(增刊1)：20-28.(Hydrologica Forecasting Techniques Group of National Hydrological Forecasting Techniques Competion.Verification of accuracy of watershed hydrological models and suggestions of further developing models[J].Hydrology,1999(Sup1):20-28.(in Chinese))

[18] TOBY H.近代科学为什么诞生在西方？[M].2版.北京：北京大学出版社，2010.

Discussion of watershed hydrological model

RUI Xiaofang

(College of Hydrology and Water Resources, Hohai University, Nanjing 210098, China)

The hydrological principle of the structure and parameters of watershed hydrological models, the physical coupling relationship between the structure and parameters, and the essential difference between lumped and distributed watershed hydrological models were investigated. The characteristics of the solution methods for these two models, and the reasons causing the phenomenon of equifinality for different parameters during the calibration of the watershed hydrological models, as well as methods to alleviate the effects of this phenomenon, are discussed. A method for verification and comparison of the watershed hydrological models is proposed.

watershed hydrological model; lumped model; distributed model; equifinality for different parameters; big data

国家自然科学重点基金(41430855);国家重点研发计划(2016YFC0402700)

芮孝芳(1939—)，男，教授，主要从事水文水资源研究。E-mail:jiangguo@hotmail.com

10.3880/j.issn.1006-7647.2017.04.001

P333

A

1006-7647(2017)04-0001-07

2017-04-28 编辑：熊水斌)