动车组天线梁随机振动疲劳寿命评估

徐 杰 肖守讷 阳光武

(西南交通大学牵引动力国家重点实验室,610031,成都∥第一作者,硕士研究生)



动车组天线梁随机振动疲劳寿命评估

徐 杰 肖守讷 阳光武

(西南交通大学牵引动力国家重点实验室,610031,成都∥第一作者,硕士研究生)

为对动车组天线梁的随机振动疲劳寿命进行评估,首先,建立天线梁及构架结构有限元模型,并对其分析得到天线梁的固有频率;然后,利用软件编程得到德国低干扰轨道不平顺自功率谱,再根据自功率谱得到各轮对间互功率谱;最后,在有限元分析软件中对各轮对进行激励加载,采用模态叠加法对天线梁进行随机振动疲劳寿命分析,得到结构疲劳寿命薄弱位置。

动车组; 天线梁; 振动疲劳; 寿命评估

Author′s address State Key Laboratory of Traction Power,Southwest Jiaotong University, 610031,Chengdu,China

结构振动疲劳是指结构受到频率与自身固有频率相近的动态载荷作用所产生的破坏[1]。振动疲劳现象在轨道交通车辆结构(构架及车轮等)中十分常见。引起车辆振动的主要原因就是轨道不平顺[3]。

天线梁通过螺栓固定在列车一位转向架构架的端部,其在列车运动过程中承受了来自于构架端部传递的振动激励。这些来自构架端部的随机振动激励很容易导致天线梁疲劳破坏。保证天线梁的安全服役至关重要,这关系着列车的行车安全。本文重点研究轨道不平顺对天线梁寿命的影响,同时还特别分析了前后轮对的时延性。结合天线实际安装情况,建立车体、构架及天线梁的整体有限元模型。对天线梁进行疲劳寿命分析,使之更好地满足工程需求。

1 随机振动疲劳理论

结构破坏发生在危险位置,危险位置的应力功率谱密度(PSD)可用G(f)来表示[4]。通过应力功率谱来构建结构应力变程σi的概率密度函数p(σi),最后利用线性疲劳损伤准则获得疲劳寿命T。

线性疲劳损伤准则基于Miner假设

(1)

式中:

D——疲劳损伤；

nσi——应力变程σi下的循环数;

Nσi——应力变程σi下的平均循环数;

Δσ——应力区间;

N——应力变程的平均循环数。

将式(1)转换为积分表达式:

(2)

式中:

σ——应力变程；

C、m——疲劳特性常数;

N0——单位时间内应力以正斜率通过零值的数目。

工程运用中,p(σ)常采用Dirlik的经验表达式[5]。令mi表示G(f)的i阶矩,则有

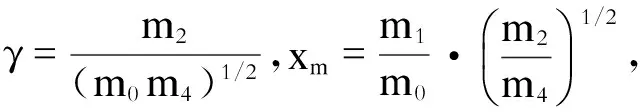
(3)

(4)

由式(3)可得,当疲劳损伤D=1时

(5)

2 天线梁随机振动寿命分析

2.1 有限元模型

结合转向架构架与天线梁的几何形状、受力特点以及对计算精度的要求,选用实体单元分布对构架和天线梁进行离散。采用10 mm大小的六面体单元对天线梁进行离散,采用15 mm大小的四面体单元对构架进行离散。天线梁各部件主要采用电弧焊连接。在天线梁模型中不直接构建焊缝的形状,分析时提取质心位于焊趾处单元的应力作为焊缝的名义应力,以尽量避免焊缝造成的应力集中,并在天线梁表面附着一层薄壳单元,以模拟焊缝单元的表面应力。构架及天线梁上承载的设备均以集中质量的形式加载在各自的质心位置。车辆轮对均以梁单元简化,一系、二系的弹簧及减震器分别用CELAS2和CDAMP1单元来代替。有限元模型如图1和图2所示。

图1 构架天线梁整体有限元模型

图2 天线梁及整车模型

2.2 轨道不平顺输入

轨道不平顺是指用来支撑和引导车轮的轨道接触面沿轨道长度方向和理论平顺轨道面之间的偏差。列车在轨道上行驶受到的振动主要来源于轨道的不平顺、车轮缺陷及轮轨冲击等外部因素。轨道不平顺随机特性统计包含轨道不平顺的幅值统计和轨道不平顺的功率谱统计。本文采用德国高速竖向轨道功率谱来描述轨道的不平顺。在直线段的轨道不平顺可以分为轨道竖向不平顺、水平不平顺、方向不平顺和轨距不平顺4种类型。

本文采用的德国高速竖向轨道功率谱均以空间频率给出,在应用过程中需转换成时间频率下的轨道功率谱。德国高速轨道竖向功率谱的竖向轨道不平顺数学表达式为[6]:

(6)

式中：

Av——表征不平顺的参数;

Ωr——较小截断频率,一般取0.020 6 rad/m;

Ωc——较大截断频率,一般取0.824 6 rad/m;

v——列车速度;

Ω——空间波数。

因Ω=vω,ω=2πf,Ω=2πf/v(其中,ω为角频率，f为频率)，则根据能量守恒定律有S(f)df=S(Ω)dΩ。故竖向不平顺表达式为:

(7)

则经转化后为:

简化后的单节车运动模型如与3所示。本文评价的列车运行速度为300km/h。根据文献[6]可知,300km/h及以上运行速度的动车组天线梁寿命预测应采用德国低干扰功率谱。经转换后的德国低干扰轨道竖向激励、水平激励和方向位移激励如图4—图6所示。

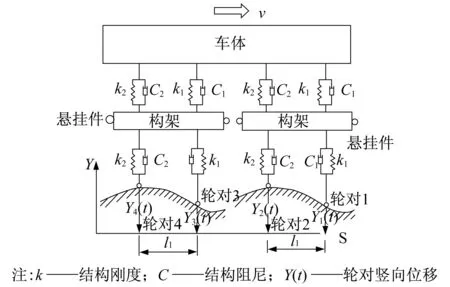
图3 单节车运动简化图

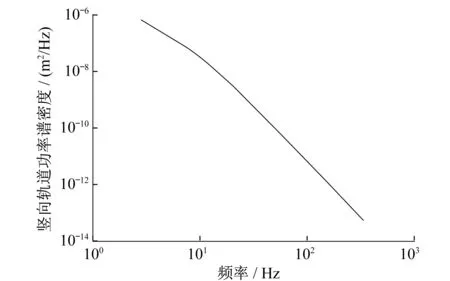
图4 轨道竖向不平顺功率谱

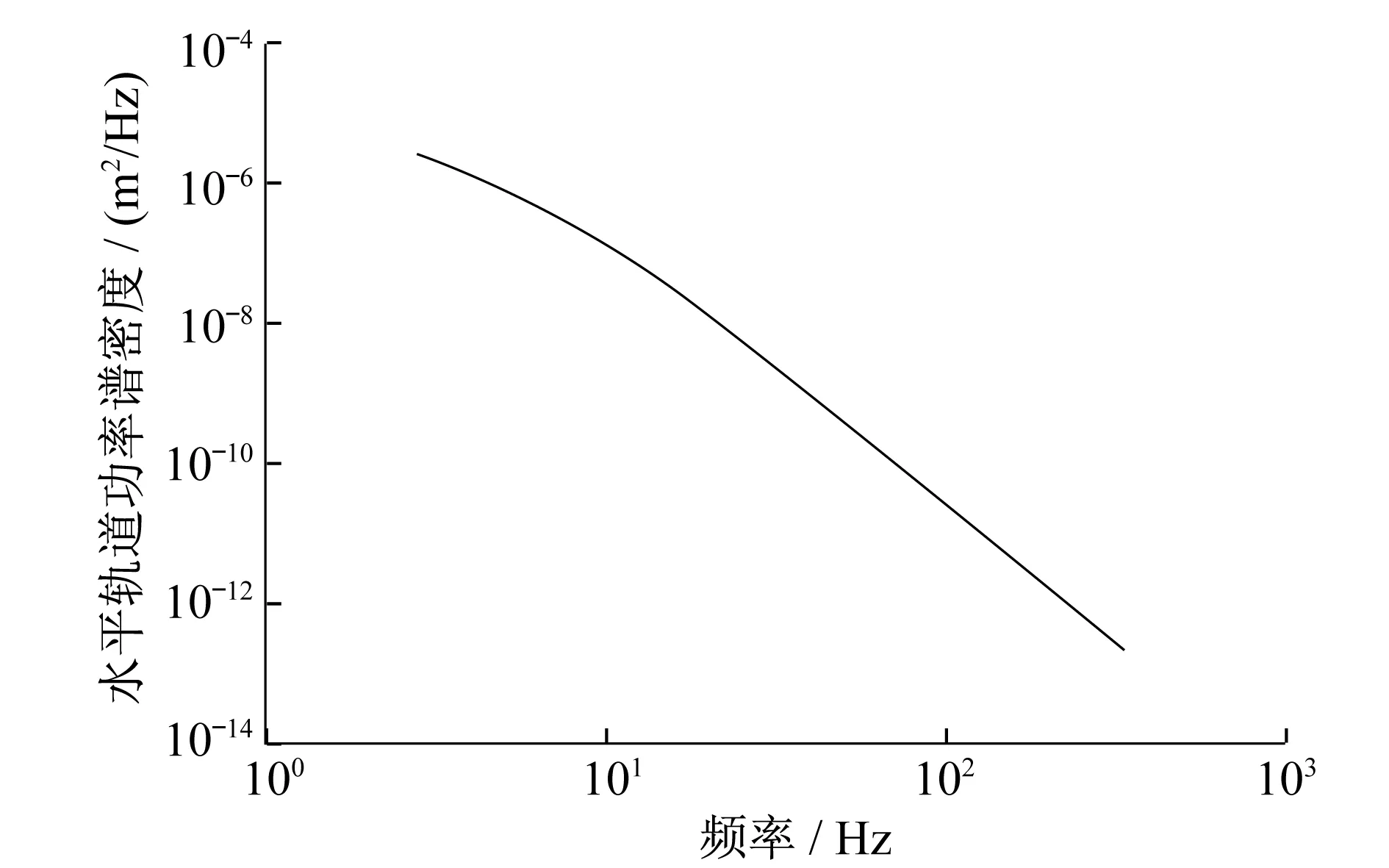
图5 轨道水平不平顺功率谱

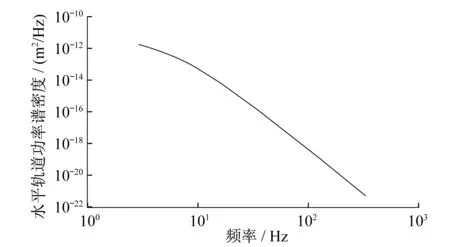
图6 轨道方向不平顺功率谱

假设轮对距轨面的高度分别为Z1(t)、Z2(t)、Z3(t)和Z4(t),单节车辆运动简化示意图如图6所示,则其轨道竖向不平顺功率谱密度SZ1(ω)=SZ2(ω)=SZ3(ω)=SZ4(ω)。当列车以速度v向前行驶时,前后轮时差τ0=l/v(其中l为转向架中心

距即车辆定距),故轮对1和轮对2的高度变化存在相关性[7]:

Z2(t)=Z1(t-τ0)

相关函数:

RZ1，Z2(τ) =E[Z1(t),Z2(t+τ)]

=E[Z1(t),Z1(t+τ-τ1，2)]

=RZ1(τ-τ1，2)

式中：

τ——轮对间的时延;

τ1,2——轮对1和轮对2的时差;

E[a,b]——a、b两者之间的期望值;

RZ1——轮对1的自相关函数。

互功率谱密度:

exp[-jω(τ-τ1,2)]·

d(τ-τ1,2)exp(-jωτ1,2)

=exp(-jωτ1,2)SZ1(ω)

用矩阵表示的轮对1和轮对2竖向位移激励为:

上述只考虑了轮对1和轮对2之间的时差,同样,轮对1和轮对3,轮对1和轮对4,轮对2和轮对3,轮对2和轮对4,轮对3和轮对4之间都存在时差:

τ1,2=τ3,4=l/v

τ1,3=τ2,4=l1/v

τ2,3=(l-l1)/v

τ1,4=(l+l1)/v

式中:

l1——轴距;

l2——车辆滚动圆横向跨距。

同理可得,四轮对竖向不平顺矩阵、方向不平顺矩阵和水平不平顺(直线上水平不平顺可以理解为绕x轴的转动即转动功率谱)矩阵为:

2.3 天线梁随机振动寿命分析结果

2.3.1 模态分析

为使结构响应在其固有频率附近聚集,以便更好地模拟结构与激励共振频率下的应力分布,随机振动分析采用模态叠加法,前、后天线梁模态分析结果见表1及表2。

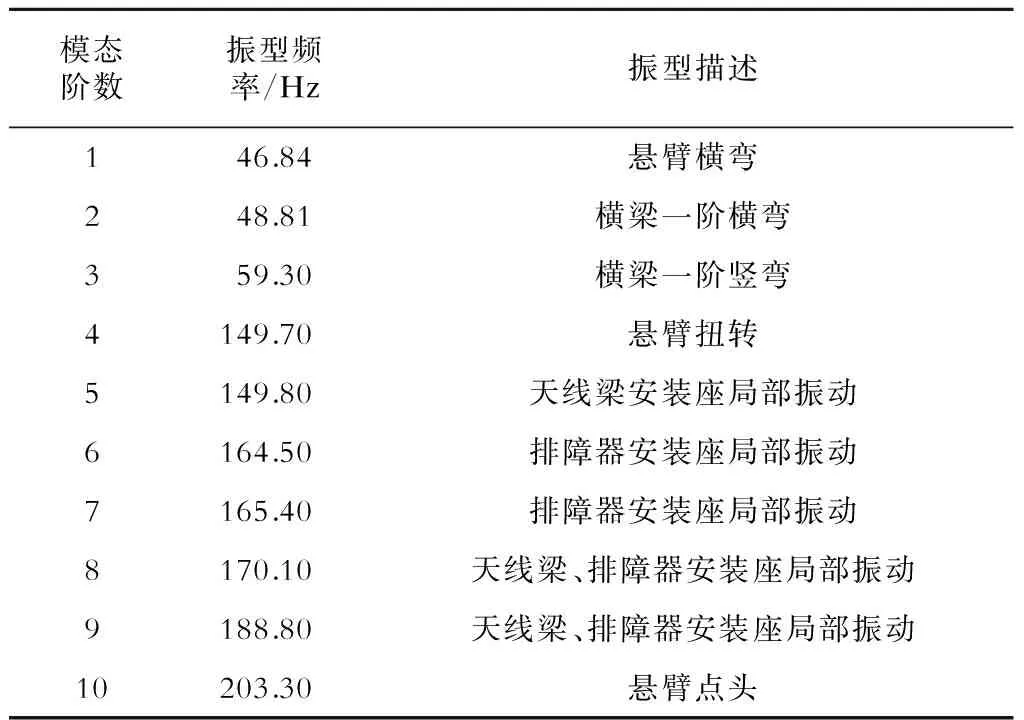
表1 前天线梁模态分析结果

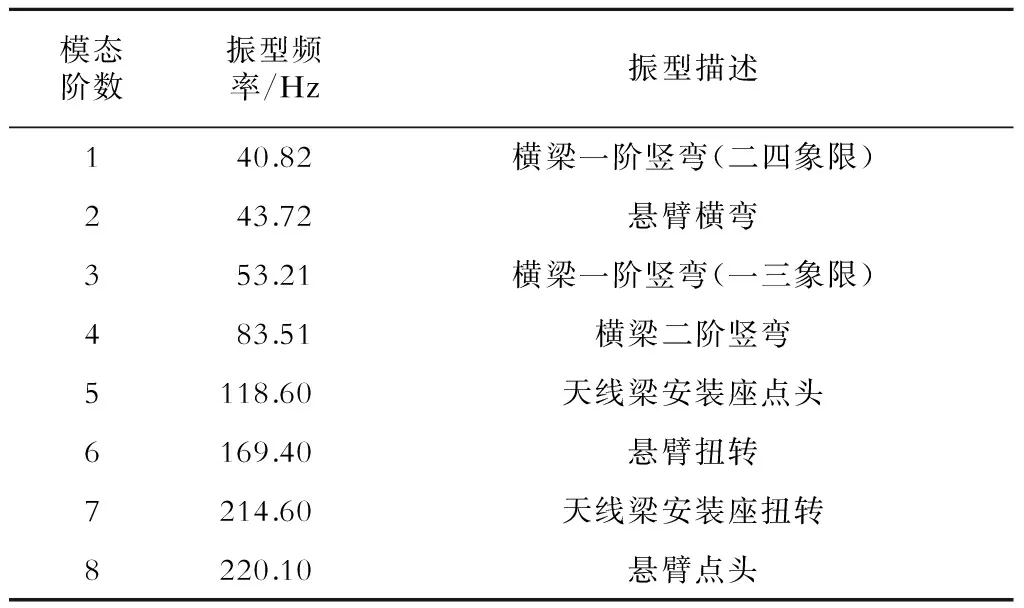
表2 后天线梁模态分析结果

2.3.2 随机振动寿命分析结果

分别将左右轨道不平顺的平均值作为输入值,同时将激励施加在2个转向架的4个轮对中心位置(如图7所示)。激励包括轨道竖向不平顺自功率谱和互功率谱、方向不平顺自功率谱和互功率谱以及水平不平顺自功率谱和互功率谱。天线梁在各向轨道不平顺共同激励作用下损伤最大的前4个单元及T型焊缝位置见表3,前、后天线梁损伤分布及其疲劳薄弱点应力功率谱如图8～图11所示。

图7 约束及激励施加位置

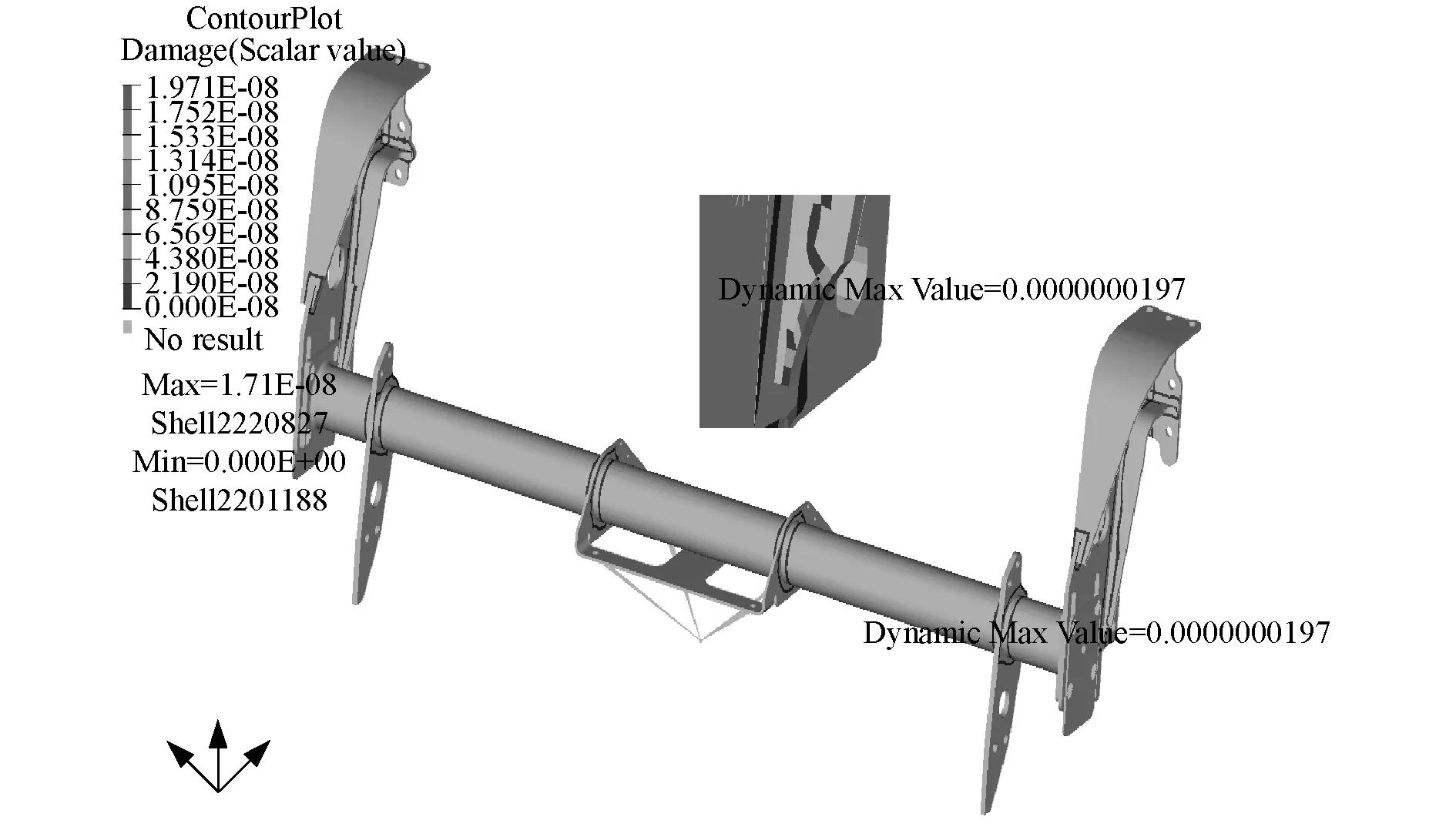
图8 前天线梁每秒损伤分布图

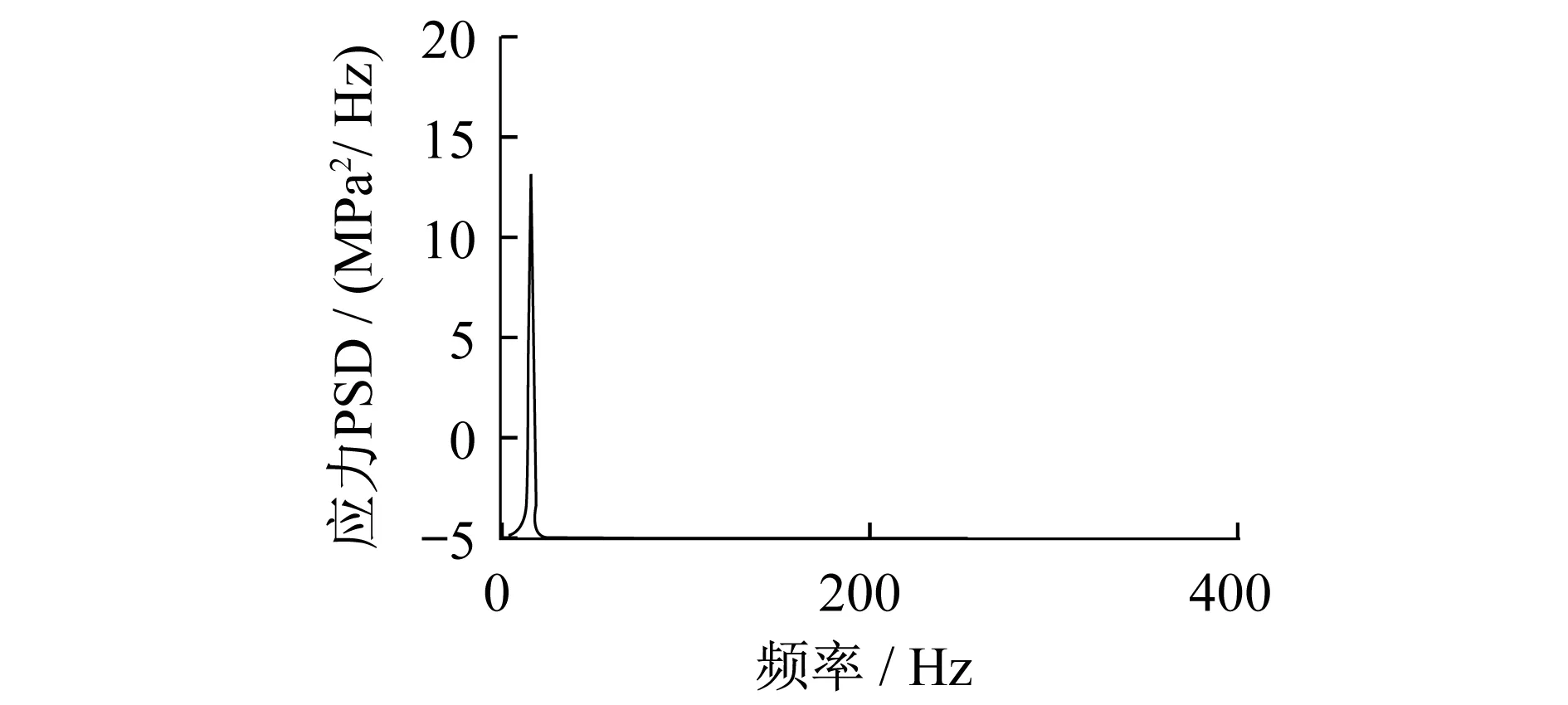
图9 前天线梁疲劳薄弱点应力功率谱密度分布

图10 后天线梁每秒损伤分布

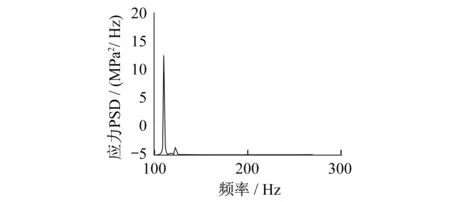
图11 后天线梁疲劳薄弱点应力功率谱

单元编号寿命/s运行里程/km疲劳薄弱位置30041103.519×107293后天线梁下盖板与立板T型焊缝22241143.658×107305前天线梁上盖板与立板T型焊缝4637073.978×107317前天线梁下盖板与立板T型焊缝4608304.321×107360后天线梁端板与下盖板T型焊缝

3 结论

通过建立前、后天线梁有限元模型,可得到天线梁的固有频率。采用德国低干扰轨道功率谱,并考虑前后轮的时延性,可得到德国低干扰轨道功率谱各自轮对间的自功率谱和互功率谱。分析前、后天线梁在轨道不平顺作为激励作用下的应力及动态响应,其结果表明:如前、后天线梁一阶、二阶固有频率同不平顺载荷频率接近,则会引起较大共振损伤。在轨道不平顺振动作用下,前天线梁疲劳损伤最大值位置为悬臂上盖板与立板T型焊接部位,后天线疲劳损伤最大值位置为天线梁安装座与横梁焊缝、悬臂下盖板与立板上下端焊接部位。设计人员应对疲劳损伤最大处予以重视,必要时需对结构进行修改。

天线梁寿命分析计算采用的是速度恒定的德国低干扰轨道功率谱。这与真实情况有所差别,列车实际运行中起动、运行、制动之间的速度都是不一样的。因此，本文计算的结果偏于保守,要使计算寿命与实际寿命更加接近,需要统计出车辆在不同速度等级下所运行的里程和轨道功率谱的实际情况。这将作为下一步研究的内容。

[1] 刘文光,陈国平，贺红林，等.结构振动疲劳综述[J].工程设计学报，2012,19(1):1-8.

[2] 李晓明,孙志鹏.动车组天线梁结构优化设计[J].铁道车辆,2011(11):22-24.

[3] 袁博.高速动车组转向架关键部件性能分析[D].大连：大连交通大学，2012.

[4] 孟凡涛,胡愉愉.基于频域法的随机振动载荷下飞机结构疲劳分析[J].南京航空航天大学学报，2012，44(1)：32-36.

[5] 李超.基于功率谱密度的疲劳寿命估算[J].机械设计与研究,2005,21(2):6-8.

[6] 张卫华.机车车辆动态模拟[M].北京:中国铁道出版社 ,2007 :90-93.

[7] 刘建树.高速列车转向架构架频域疲劳寿命分析[D].成都:西南交通大学,2011.

Evaluation of the Random Vibration Fatigue Life for Bullet Train Antenna Beam

XU Jie, XIAO Shoune, YANG Guangwu

A finite element model of antenna beam and truck frame structure is set up to evaluate the random vibration fatigue life of bullet train antenna beam,the natural frequency of the antenna beam through model analysis is obtained. Then,the auto-power spectrum of Germany low interference track spectrum is obtained by software programming,which is used to get the cross-power spectrum for each wheel.Finally,each wheel is incentive loaded in finite element analysis software,and the random vibration fatigue life of antenna beam is analyzed by using model superposition method.Thus,the weak position in antenna beam structure is detected.

bullet train; antenna beam; vibration fatigue; life evaluation

U266.281

10.16037/j.1007-869x.2017.06.013

2015-02-28)