基于移动实时位置信令数据的轨道交通换乘行为分析

黄天印 徐文洁 陆林华 赵时旻

(1.上海申通地铁集团有限公司,201103,上海; 2.上海久誉软件系统有限公司,200233,上海∥第一作者,高级工程师)



基于移动实时位置信令数据的轨道交通换乘行为分析

黄天印1徐文洁1陆林华2赵时旻1

(1.上海申通地铁集团有限公司,201103,上海; 2.上海久誉软件系统有限公司,200233,上海∥第一作者,高级工程师)

介绍了上海轨道交通清分规则。在现有上海轨道交通K条最短路径的清分算法基础上,融合移动实时位置信令(OIDD)数据,对换乘行为中的主要换乘路径选择比例进行精细化设置,并对次要换乘路径的换乘比例算法作出补充。通过对乘客行为的分析和应用,实现了对现有上海轨道交通清分规则中换乘路径比例的精细化计算。

轨道交通; 移动实时位置信令数据;K条最短路径; 清分算法

First-author′s address Shanghai Shentong Metro Group Co., Ltd.,201103,Shanghai,China

2016年,上海城市轨道交通路网总长度达617 km,包括14条线路和366座车站。其中,换乘车站有51座。随着上海城市轨道交通出行路线选择的多样化,客流出行模式从先前的同线出行或一次换乘出行转变为同线出行、一次换乘为主、多次换乘为辅的混合模式。这种模式的转变使轨道交通运营方对轨道交通换乘客流及票价清分的精细程度提出了更高要求。

1 上海轨道交通票务清分规则

上海轨道交通票务的清分模型主要依据基础数据建立、路网路径选择和路径比例分配等3部分内容。基础数据主要包括线路与车站名、站间距、区域表、换乘站设定、换乘步行时间、列车平均行驶速度、收益方及比例、拥挤系数等[1]。路网路径选择采用基于Dijkstra算法的K条最短路径法(KSP)。首先,通过Dijkstra算法计算K条路径;然后,结合“换乘权”优化处理,剔除大于最小路径(计算权)1.5倍的路径,从而得到每对OD记录(起终点间的出行量)最多K条路径(包含换乘次数、总权重、实权、虚权、计算权)。通过使用“正态分布方式”可得到各路径比例[2-3]。

现有的上海轨道交通的清分模型是基于经验权重值计算的概率分布模型,其在换乘路径比例(即选择某换乘路径的客流量占总换乘客流量的比例)的精细化程度上有进一步提升的空间。

本文所使用的数据资源覆盖时间范围从2015年4月1日至2015年4月30日,包括近27万条电信OIDD (移动实时位置信令)数据,近4亿条检售票系统交易数据,以及近340万条ATS (列车自动监视)系统数据及轨道交通运营计划图数据。

2 乘客出行路径选择的相关研究

理解乘客出行的路径选择行为是一个重要的研究方向[5-8],其研究成果可应用于许多场景。

交通领域中很早就有人对这一问题进行了研究。典型的研究模型为UE (单位经济)模型[9]和MPS (物质产品平衡表体系)模型[10]。然而,许多已有工作多是基于经验的模型假设,缺乏数据支持[11-12]。随着智能交通卡广泛使用而生成的大量数据有助于进一步解决这一问题。在城市轨道交通中,智能交通卡数据不同于GPS (全球定位系统),某个OD (起讫)对间的乘客换乘选择是没有被记录的,所以不能直接从数据中得到的结果。

文献[13]利用经验模型作为先验知识,提出了一种基于贝叶斯推理的框架来解决路径选择这一问题。文献[14]利用遗传算法对路径选择问题进行了优化处理。这类方法结合了历史数据,其模型精度较基于经验的模型有较大提升。但是,不可避免的,这些方法均以经验模型作为先验知识,故在一定程度上仍会受到经验的影响。

文献[15]在预先知道特定OD对候选路径的情况下,通过K-means聚类方法,统计不同路径上的乘客数量,从而得到乘客路径选择的结果。文献[16]将乘客的刷卡数据与城市轨道交通的营运时刻表相结合,从而识别乘客的换乘行为。这类方法避免了先验知识的影响,但处理数据稀疏的OD对时,其模型的准确度会受到影响。

大量的OIDD数据可为城市轨道交通乘客匹配精确的位置信息,为实现乘客换乘行为的识别提供了支持。

3 OIDD数据与轨道交通换乘行为的匹配

3.1 OIDD数据

OIDD数据涵盖了用户手机联络基站的时间、基站号、联扇区号、开关机信息等。在有通信行为时,手机还可通过心跳方式定期与基站联络,产生OIDD数据。也就是说,即使用户没有任何通信行为,只要开机,就可定期获得用户的大致位置。

使用OIDD数据,可在一定的时间周期内估测任意区域内的人数,可估测任意区域或路线上的人流车流,可用于分析大型活动期间人流的来源、去向及公交换乘链等信息,可根据电话归属地和用户注册信息来分辨本地用户或外地游客。

3.2 OIDD数据的设备定位方法

目前,根据OIDD数据进行设备定位主要采用COO(cell of origin)方法,即通过单个基站ID(cell ID)定位。该方法计算简单,速度极快。但定位精度与基站的覆盖半径R有关(如图1所示)。监测区域内基站分为宏站、街道站和微站。利用COO方法进行定位时,如数据来自宏站,则误差相对较大;如来自街道站和微站,则精度相对较高。

通过优化COO方法可进一步提高了OIDD数据定位精度。优化方法主要利用了信号跳变,并基于以下三个假设条件:①信号跳变由目标的移动引起,而非干扰;②任何基站的覆盖范围及信号发射强度相同,且不受建筑物和天气因素的影响;③周边建筑物、电网及电力电子设备等对电磁波无干扰。

优化后,OIDD定位时,设某人的周围有k个基站,且基站的坐标集为 {P1(x1,y1),P2(x2,y2),…,Pk(xk,yk)}。其中,Pi代表第i个基站,(xi,yi)表示第i个基站的经纬度坐标。在某一段时间内,此人的手机信号在这k个基站间来回跳变。由优化方法的假设可得,当信号在2个基站间跳变时,人所在位置在平面上的分布必为对称分布,且位置的期望必为两基站连线的中心,从而实现定位(如图2所示)。

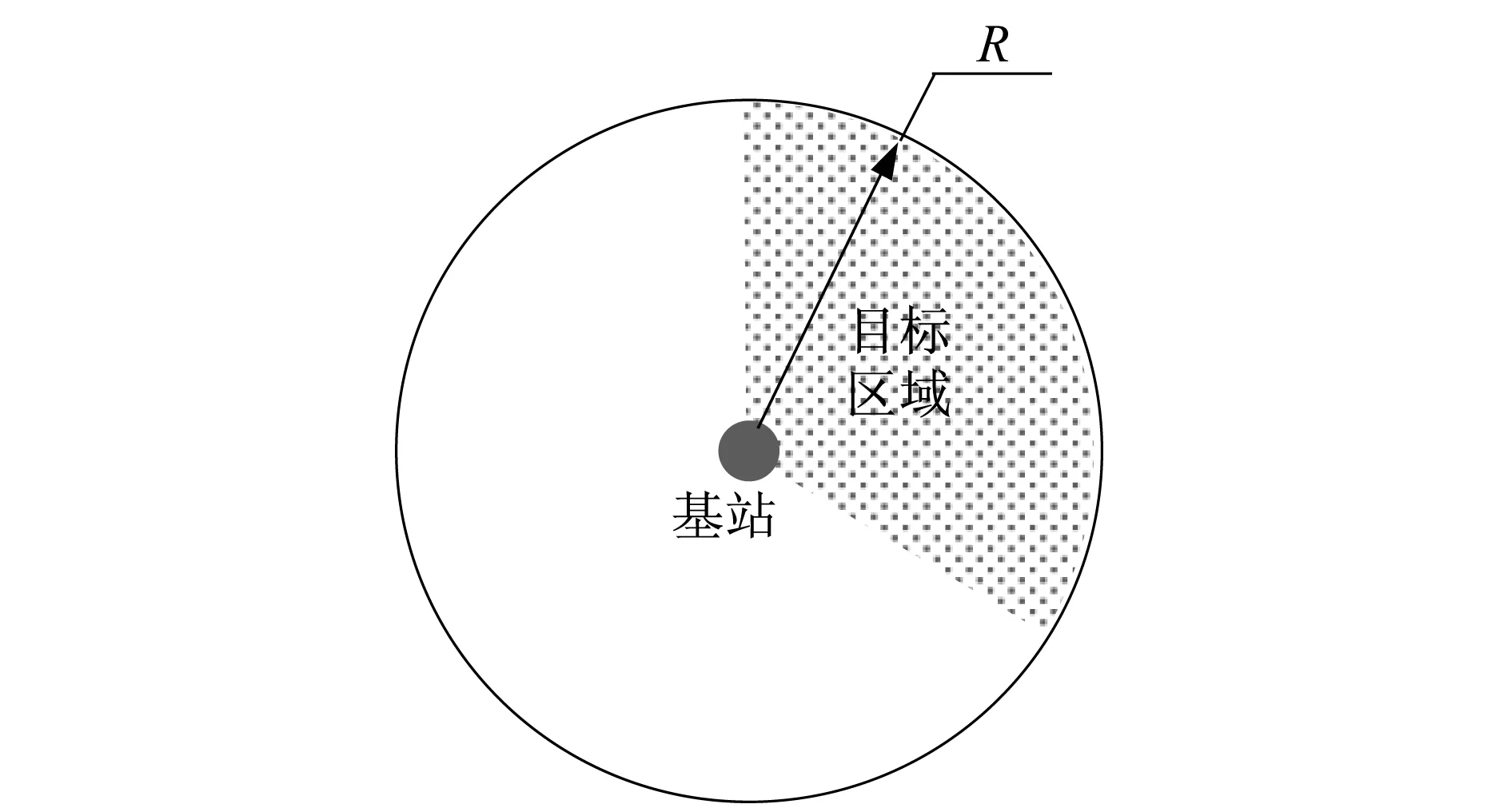
图1 COO定位方法

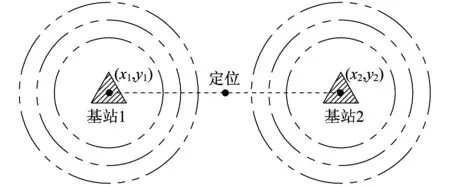
图2 当信号在2个基站间跳变时的定位

3.3 基于OIDD的乘客OD数据统计

在OIDD数据基础上,可进一步分析统计乘客换乘出行OD数据。具体的计算方法及步骤如下。

步骤1:从OIDD数据中抽取在城市轨道交通起始车站及其周围出现的数据集{O1,O2,…,Oi}。

步骤2:按步骤1的方法抽取在目的地车站及其周围出现的数据集{D1,D2,…,Di}。

步骤3:找出步骤1和步骤2所得数据的交集σ={O1,O2,…,Oi}∩{D1,D2,…,Di},即可找出从起始站上车和目的地站下车的人。

步骤4:根据步骤3的数据交集σ,分析出现在目的车站及其周围的时间和出现在起始车站及其周围的时间,并抽取时间间隔在15～90 min范围内的数据集R={σt1,σt2,…,σti},15 min≤ti≤90 min;

步骤5:将一天按5 min刻度划分为288个等级,将满足步骤4的数据集分别划分到这288个等级中,并统计各个等级中不同的数据集量值。最终即可得到基于OIDD数据的分时段OD客流。

其中,步骤3起始站上车和目的站下车的判断规则为:如该人从起始车站及其周围出现前60 min内没有出现在其他车站,则视为该人为从起始车站上车;当该人从目的车站及周围出现后的60 min内没有出现在其他车站,则视为该人为从目的车站下车。

3.4 OD数据的匹配处理

不同年龄的人具有不一样的移动终端设备使用习惯。小孩、老人与青年人相比较差异性很大。此外,人们使用手机的行为或习惯也不一致。有些人手机常关机或手机通话较少。而且手机数据采集技术本身也会漏抓部分数据。因此基于手机数据的出行行为分析针对的人群并不能表示总体人群。因此,需要将抽样数据扩样至总体人群的出行数据,进而反映总体人群的出行特征与出行规律[4]。

以上海轨道交通九亭站至人民广场站(以下简为“九亭—人民广场”)的路径为例分析,将在该路径上涉及的相关换乘车站电信基站作为采样基站。则详细统计结果如表1所示。

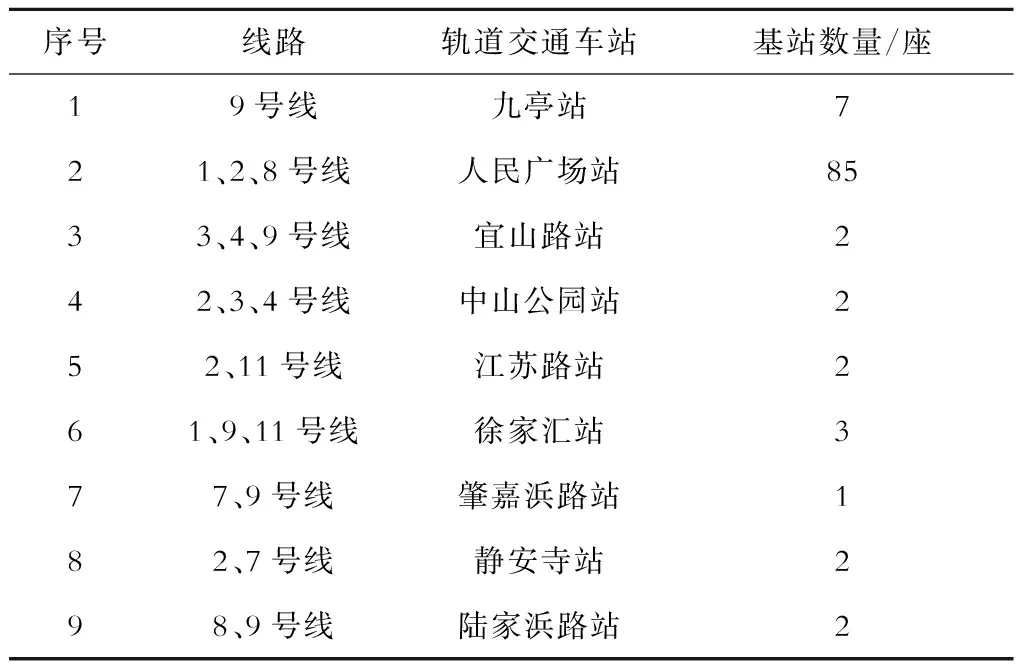
表1 九亭—人民广场路径基站数量统计

以2015年4月期间九亭—人民广场的OIDD数据作为扩样样本数据。首先,根据城市轨道交通的运营时间,将OIDD数据整理出OD数据;然后,将得到的结果与九亭—人民广场的售检票系统OD数据进行对比。对比结果如图3所示。

售检票系统数据处理采用多层扩样模型。以轨道交通售检票系统数据作为基准数据,先以单日样本进行扩样计算,再通过时间序列平滑法得到月平均扩样值。

时间序列是数理统计的重要分支,在经济发展和工业建设方面有着重要应用。时间序列是指在研究过程中,在一系列时刻(t1,t2,…,tn)对某1个或1组变量进行测量,得到的测量值序列。

图3 2015年九亭—人民广场基于售检票系统OD数据与基于OIDD的OD数据对比

时间序列平滑法是指用平均的方法,把时间序列中的随机波动剔除掉,使序列变得比较平滑,以反映出其基本轨迹,并结合一定的模型得到目标计算值。时间序列平滑法所用平均数可以是简单平均数,也可以是加权平均数。在第一次平均计算之后,就局部而言,还可进行第二次、第三次以至更多次的平均计算,以实现多层次的平滑。时间序列平滑法计算如式(1)所示。

F(T+1)=(1/N)×∑X(I)

(1)

式中:

X(I)——时间序列的第I期实际值;

F(T+1)——目标计算值;

T——当前时刻;

T+1——目标时刻;

N——平均个数。

通过对扩样值的平滑平均计算,即可得到合适的扩样比例。以2015年4月期间九亭—人民广场的OD数据为例分析,得到扩样值序列如表2所示。根据表2及式(1)可得,平均扩样比例为1∶6.95。

3.5 融合OIDD数据后的换乘路径比例

以九亭—人民广场路径为例,根据K条最短路径法计算可得,到九亭—人民广场可选择的换乘路径为9号线换乘1号线(徐家汇站换乘),9号线换乘8号线(陆家浜路站换乘),9号线换乘7号线(肇嘉浜路站换乘)再换乘2号线(静安寺站换乘),9号线换乘3/4号线(宜山路站)再换乘2号线(中山公园站换乘)。

对九亭—人民广场的IODD数据进行采集分析,得到不同的换乘路径比例(见图4)。

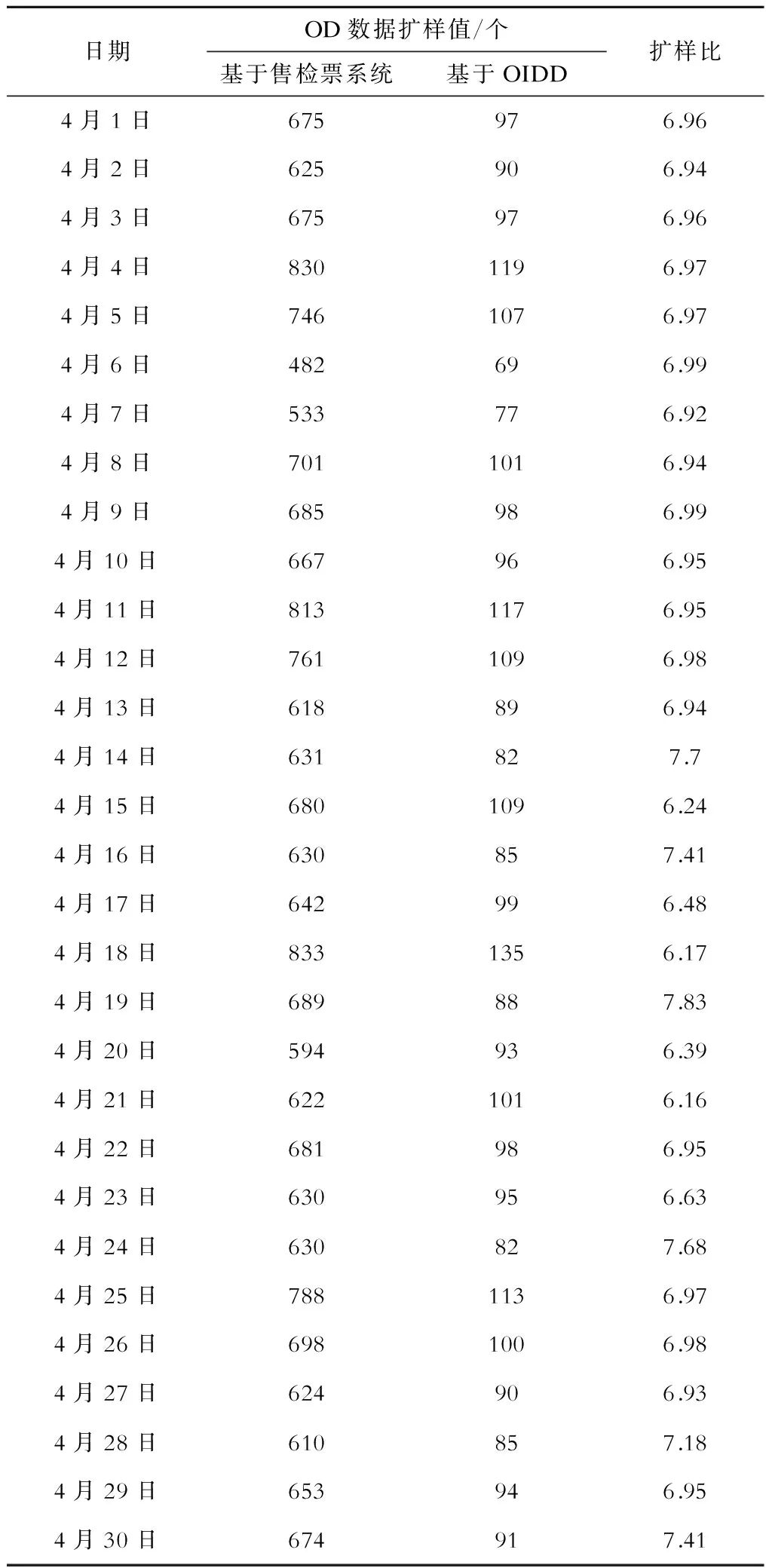
表2 基于售检票系统的数据OD和基于OIDD的OD数据扩样值及扩样比

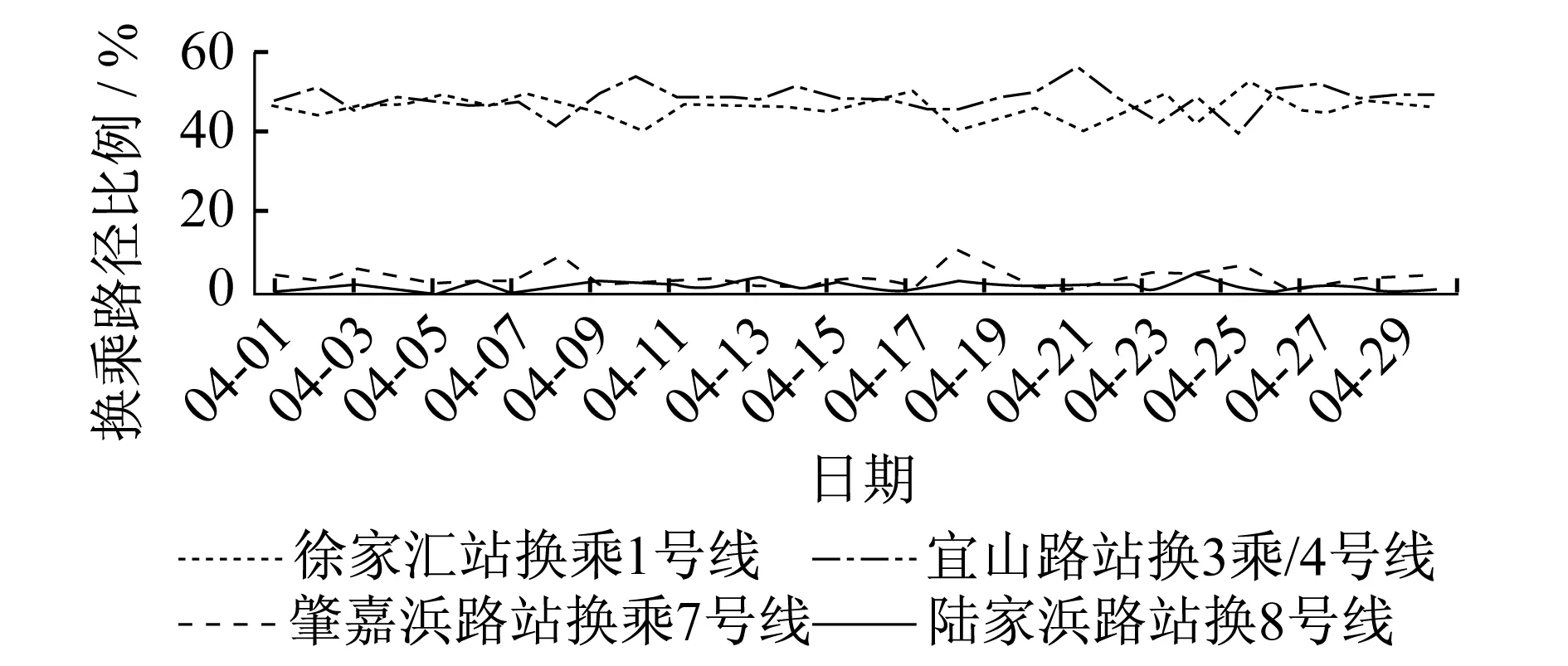
图4 2015年4月九亭—人民广场换乘路径比例

分别通过现有上海轨道交通清分算法,以及IODD数据权重分析后的清分模型,可计算得到九亭—人民广场的换乘路径比例(如表3所示)。

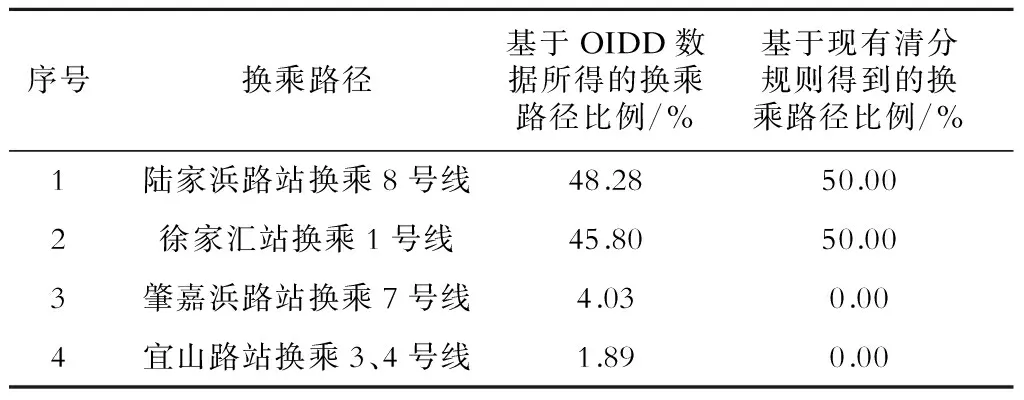
表3 通过不同计算依据得到的换乘路径比例

由表3可见,按现有清分规则,选择在陆家浜路站换乘8号线及在徐家汇站换乘1号线的客流量各占总客流量的50%,而选择在肇嘉浜路站换乘7号线和在宜山路站换乘3、4号线的比例均为0。这显然不符合实际情况。

因此,基于OIDD数据计算的结果更精细,而且在二次换乘的路径比例设置上也有补充。

4 不同时段的换乘比例情况分析

4.1 时段的划分

由于乘客在不同的时段(如工作日、节假日,或高峰时段、其他时段等),其出行的目的和对出行的路径选择会有差异。因此,轨道交通线路的换乘比例也会变化。根据工作日和非工作日上海轨道交通各线路的换乘情况,工作日的乘客换乘比例通常比非工作日高出约10% (如图5所示)。

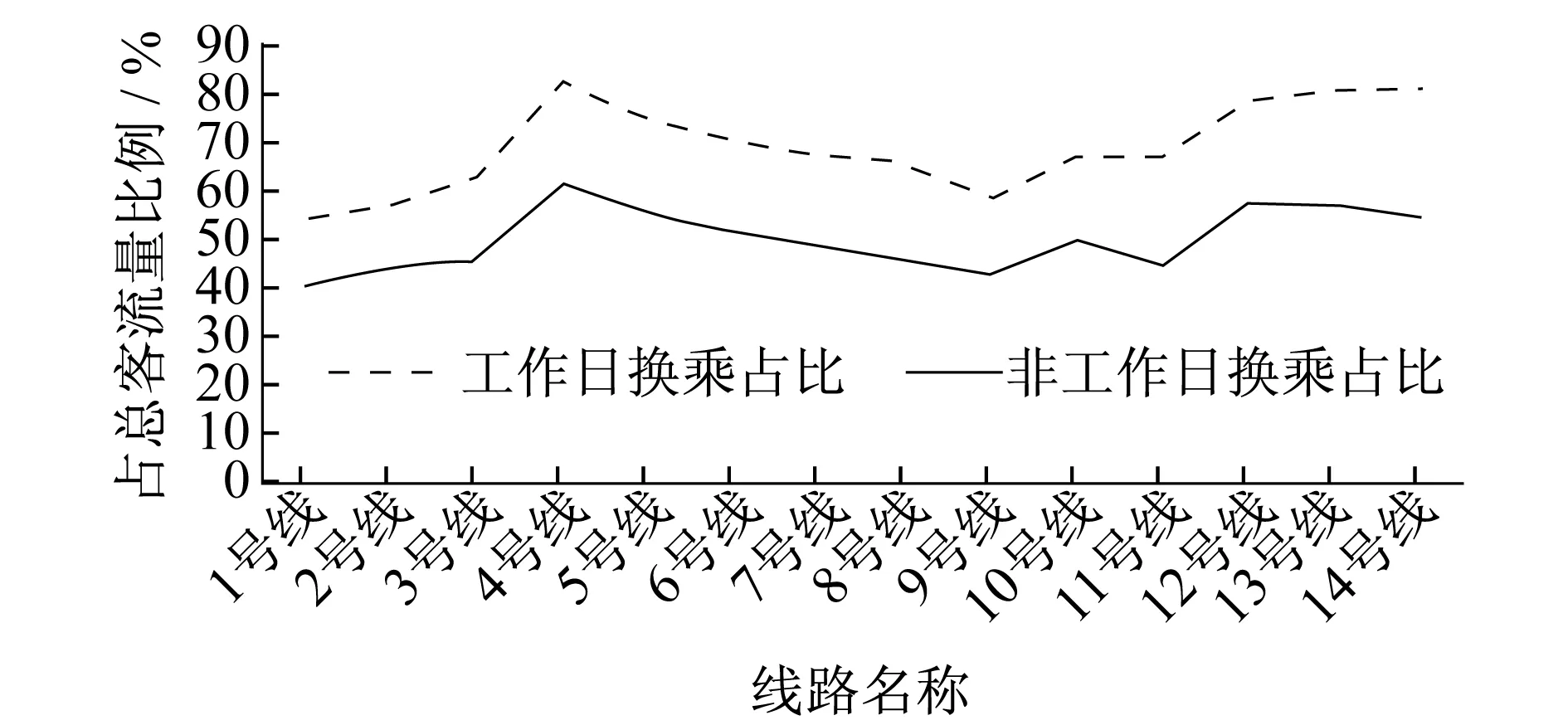
图5 工作日及非工作日上海轨道交通各线路换乘比例

在工作日期间,高峰时段(6:30—9:30及17:00—19:00)的出行客流量是低峰时段(除高峰时段外的其他时段)的1.6倍左右。而且,高峰时段的乘客出行目的与低峰时段不同,乘客对于换乘路径的选择也可能存在差异。针对这种情况,本文采用融合OIDD数据的计算方法,对工作日、非工作日,以及工作日中不同时段的换乘比例进一步研究。

以九亭—人民广场为OD段,分别统计工作日及非工作日的换乘比例。

分析高低峰客流换乘情况采用的方法是将OIDD客流密度扩样数据根据0.5 h时间维度进行细分。然后,以6:30—9:30及17:00—19:00作为高峰时段,其余时段作为低峰时段进行分析。

4.2 处理逻辑

对OIDD数据处理逻辑查询包含3层嵌套。

(1) 第1层嵌套。对九亭—人民广场基于OIDD的OD客流量数据表进行处理,获取记录中的进站代码、日期、高低峰标志、进站时间、站点1代码、站点1经过时间、站点2代码、站点2经过时间、出站时间、客流量、换乘标志、30 min进站时间标示ID (将时间折算成以30 min为间隔的进位取整的整数)等字段。

(2) 第2层嵌套将第1层嵌套查询得到的记录,以日期、换乘标志及时间ID为维度来统计符合条件记录的客流总量。

(3) 第3层嵌套将第2层嵌套查询到的记录,以起始时间、结束时间、换乘标志及高低峰标志等维度来统计客流总量。

(4) 最外层将第3层嵌套查询到的记录,以换乘标志、高低峰标志、起始时间,结束时间及客流量等维度统计客流总量,以及不同换乘线路在高低峰时段的客流量占比情况。得到的数据结果(部分)如图6所示。

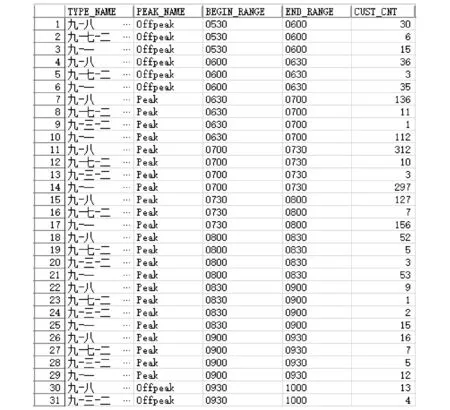
注:TYPE_NAME表示换乘线路名称;PEAK_NAME为高低峰标志;BEGIN_RANGE为起始时间;END_RANGE为结束时间;CUST_CNT为客流量;offpeak为低峰时段peak为高峰时段

根据图6所示的数据,计算换乘路径比例,得到的结果如表4所示。

表4 基于OIDD数据计算得到的九亭—人民广场高低峰时段乘客换乘路径比例

同样,将基于OIDD的客流密度数据按工作日及非工作日的时间维度进行划分,并根据划分结果计算,即可得到换乘路径比例情况(如表5所示)。

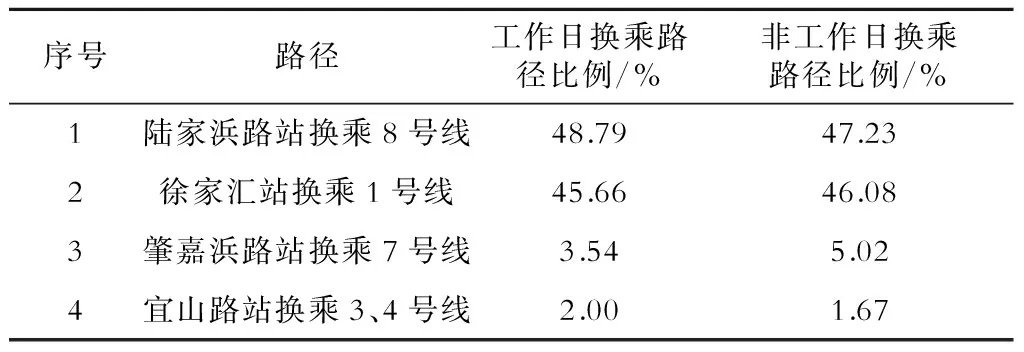
表5 基于OIDD数据的九亭—人民广场工作日及非工作日乘客换乘路径比例

由表5可以看出,乘客的出行选择会随着时段的不同而发生变化。研究换乘路径比例在不同时段的变化情况,对未来上海轨道交通的清分规则中换乘比例分配的精细化发展是有帮助的。

5 结语

本文将OIDD实测数据融入清分算法分配的权重设置中。一方面可验证现有分配比例的正确性和合理性,对现有的清分算法换乘路径比例分配算法形成补充,使得现有清分规则无论在主要换乘路径还是次要换乘路径上的比例分配都能更为精细;另一方面也可对不同场景下的换乘路径比例进行细分,为未来上海清分系统分时段调整换乘路径比例提供数据参考。

未来,还将通过OIDD数据计算全路网的换乘比例,并结合现有的轨道交通刷卡的OD数据、轨道交通ATS数据(包括进站时间、出站时间、上下行方向等)、列车满载量、车站容积率等数据,相对精确地计算出城市轨道交通客流的移动情况、客流在站台的积压程度及列车的满载率等数据。这些数据对于城市轨道交通运营方的客运组织、大客流应对,以及运能效率的规划均有较大的参考价值。

[1] 殷锡金.轨道交通网络客流清分规则与“鉴识车票乘车路径”理论[J].轨道交通,2009(12):44.

[2] 韦强,谢宗毅,诸仕荣,等.基于概率模型的轨道交通清分算法[J].城市轨道交通研究,2009(12):43-46.

[3] 顾佳源.城市轨道交通清分算法的介绍与比较[C]//中国土木工程学会城市轨道交通技术推广委员会.城市轨道交通关键技术论坛暨地铁学术交流会.上海:上海申通地铁集团有限公司,2010.

[4] 冉江宇,过秀成,何小洲.基于出行链的OD扩样方法研究[J].交通运输工程与信息学报,2010(6):37.

[5] LIU C,QU Q.Trip fare estimation study from taxi routing behaviors and localizing traces[C]//IEEE International Conference on Data Mining Workshop.Atlantic City,NJ:IEEE,2015:1109-1116.

[6] WU H,MAO J,SUN W,et al.Probabilistic robust route recovery with spatio-temporal dynamics[C]// ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. San Francisco:ACM,2016:1915-1924.

[7] LI M,AHMED A,SMOMLA A J.Inferring movement trajectories from GPS snippets[C]//Eighth ACM International Conference on Web Search and Data Mining.San Francisco:ACM,2015:325-334.

[8] SU H,ZHENG K,HUANG J,et al.Calibrating trajectory data for spatio-temporal similarity analysis[J].The VLDB Journal,2015,24(1):93-116.

[9] WARDROP J G.Some theoretical aspects of road traffic research[J].OR,1952,1(3):325-362.

[10] DIAL R B.A probabilistic multipath traffic assignment model which obviates path enumeration[J].Transportation research,1971,5(2):83-111.

[11] NAKAYAMA S,KITAMURA R.Route choice model with inductive learning[J].Transportation Research Record Journal of the Transportation Research Board,2000(1725):63-70 .

[12] TALAAT H,ABDULHAI B.Modeling driver psychological deliberation during dynamic route selection processes[C]//Intelligent Transportation Systems Conference,2006.Toronto:IEEE,2006:695-700.

[13] SUN L,LU Y,JIN J G,et al.An integrated bayesian approach for passenger flow assignment in metro networks[J].Transportation Research Part C Emerging Technologies,2015,52:116-131.

[14] ZHU H W,HU H,HUANG Z.Calibrating rail transit assignment models with genetic algorithm and automated fare collection data[J].Computer-Aided Civil and Infrastructure Engineering,2014,29(7):518-530.

[15] FU X,LENG B,XIONG Z.Metro traffic route assignment using K-means clustering[C]// International Conference on Electronics,Communications and Control.Ningbo:IEEE,2011:902-905.

[16] ZHAO J,ZHANG F,TU L,et al.Estimation of passenger route choice pattern using smart card data for complex metro systems[J].IEEE Transactions on Intelligent Transportation Systems,2016,(99):1-12.

Analysis of Rail Transit Transfer Behavior Based on Real-time Location of Signaling Data

HUANG Tianyin, XU Wenjie, LU Linhua, ZHAO Shimin

The clearing rules of Shanghai rail transit is introduced.Based on Shanghai metro clearing algorithm——K shortest path,and combined with OIDD data,a better set in the main transfer path selection is made and the ratio of the secondary transfer path selection is replenished.Through analysis of passenger transfer behavior in rail transit,the fine calculation of transfer path selection ratio in Shanghai rail transit clearing rules has been achieved.

rail transit; OIDD;Kshortest path; clearing algorithm

U293.13

10.16037/j.1007-869x.2017.06.011

2016-01-01)