基于非负张量分解的视频篡改检测方法

张雪莉，黄添强，林晶，黄维

（1. 福建师范大学软件学院，福建 福州 350007；2. 福建省大数据挖掘与应用工程技术研究中心，福建 福州 350007；3. 福建师范大学数学与计算机科学学院，福建 福州 350007）

基于非负张量分解的视频篡改检测方法

张雪莉1,2，黄添强1,2，林晶3，黄维1,2

（1. 福建师范大学软件学院，福建 福州 350007；2. 福建省大数据挖掘与应用工程技术研究中心，福建 福州 350007；3. 福建师范大学数学与计算机科学学院，福建 福州 350007）

鉴定视频的真实性和完整性是信息安全领域的重要内容之一，针对视频帧间篡改操作，提出一种基于非负张量分解的视频篡改检测方法。首先，对视频帧进行快速特征提取，利用主要压缩特征创建三维张量描述视频；然后，使用Tucker分解方法对张量进行非负分解，提取时间维因子矩阵进行相关性计算；最后，利用切比雪夫不等式自适应地定位篡改位置。实验证明，该方法能快速顽健地检测出视频帧间篡改操作。

视频篡改检测；非负张量分解；Pearson相关系数；离散余弦变换；切比雪夫不等式

1 引言

随着数码成像设备的普及和多媒体编辑软件功能的日益强大，人们可以轻易实现对图像/视频的修改。一些修改操作会使图像/视频更加美观有趣，但是其中不乏出现一些出于各种目的伪造图像/视频的情况。多媒体数据的可靠性在新闻媒体、科学发现、法庭证物等领域都有比较重要的价值[1]，因此，对多媒体数据真实性和完整性的判断就显得尤为重要。

视频取证技术主要分为主动取证技术和被动取证技术2种。主动取证技术主要通过事先对视频嵌入一些防伪信息，检查防伪信息是否遭到破坏判断视频是否遭到篡改，如水印或电子签名等。但面对如今海量的多媒体数据，主动取证技术就显得过于局限。相较而言，不需要外部嵌入信息，只通过视频本身信息进行篡改检测的被动取证技术有更为广泛的实际应用。

目前，国内外关于视频帧间篡改的被动取证技术已取得了一定的进展。文献[2]提出一种基于模式噪声的数字视频篡改检测算法，根据成像传感器的非理想性，利用维纳小波滤波器从视频中提取每帧相对稳定的残留模式噪声的平均值作为模式噪声，通过比较待鉴别帧的噪声与模式噪声之间的相关性来判定视频是否遭到篡改，但是其只能检测非同源成像设备的篡改，且不能检测视频删除篡改。文献[3]针对背景静止或运动缓慢的视频相邻帧间的纹理特征相关性大，且篡改后会一定程度上使其相关性变小的特性，通过计算相邻帧灰度共生矩阵的相关性找出异常帧，该方法适用于各种格式的视频，但不能有效检测视频删除篡改。文献[4]提出通过灰度值来表示视频帧内容，利用帧间内容的相关性连续度是否发生变化，二次利用切比雪夫不等式，自适应地设定阈值找出篡改点，但对于删除操作的检测效果不够好，容易产生漏检。文献[5]提出将待测视频序列用四维张量表示，使用Tucker分解算法分解视频张量，提取时间维度因子矩阵的每一行表示每帧内容，计算其相关性来确定是否有帧的插入或删除篡改，但其对于视频特征的表示有过多重复数据，设计不够合理。

本文针对视频相邻帧具有极强相关性的原理，对视频帧间篡改操作进行检测和定位。首先对视频帧进行快速特征提取，提取主要压缩信息形成特征矩阵，针对视频特征矩阵序列，创建三维张量对每帧特征进行描述，然后将三维张量进行非负Tucker分解，提取代表视频主要成分的时间维因子矩阵进行相关性计算，定位篡改位置。文献[5]直接将彩色视频生成四维张量处理，冗余信息过多，而本文将视频帧灰度化后进行快速特征提取，与文献[5]相比，算法计算复杂性更小，性能更好。

本文提出的检测算法不需要限制视频的格式，对成像设备也无要求，适用性强。使用快速提取帧压缩特征与张量分解的结合方法，将每帧特征由矩阵压缩为向量，计算量更小。本文算法与现有算法相比，检测时间更短、效率更高。

2 非负张量分解

张量即一个多维数组[6]，可以看作由若干个向量空间中基底的外积张成的空间。如图1所示，每个小立方体代表一个数据。

图1 张量的概念

在现实世界中，大量事物可以用张量表示，如文本数据、视频流等。一幅RGB图像就可以看作R、G、B三元矩阵组成的三维张量。张量结构在数据表达和计算方面具有良好的性能[7]，与传统数据表示方法相比，可以保证多维数据的空间结构不被破坏，在数据挖掘、化学分析、计量心理学、信号处理、数据压缩等领域有广泛的应用。

张量分解是在矩阵奇异值分解概念上的延伸[8]。目前存在CP分解、Tucker分解等多种张量分解的模型，本文采用Tucker模型对视频张量进行分解。Tucker模型是一种高阶主成分分析方法[9]，它将N阶张量分解为一个核心张量和每一维乘上一个因子的形式。

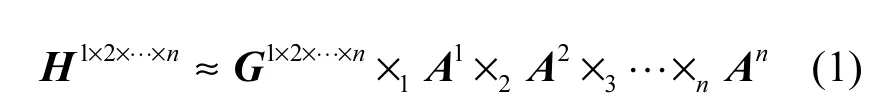
其中， G1×2×…×n为分解后的核心张量， A1,A2,…, An为每一维上的因子矩阵，可以视为该维的主要成分。

图2是三维张量的Tucker分解形式。三维张量可以分解为3个因子矩阵A、B、C和1个核心张量G，其中核心张量G看作是对原始张量X的压缩[6]，各个维度的因子矩阵可以视为该维的主要成分。在某些情况下，相较于原始张量，压缩后的张量所占用的存储空间更小。

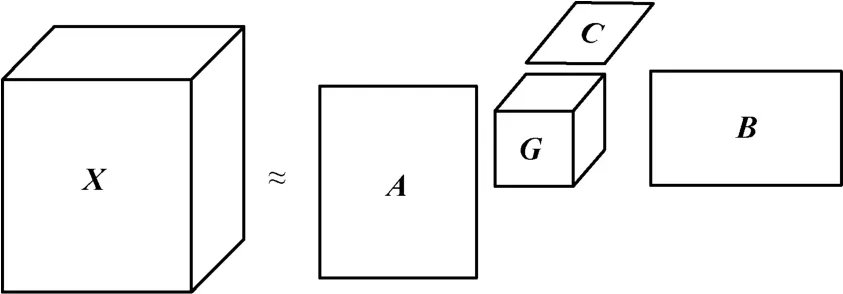
图2 三维张量的Tucker分解形式

3 篡改检测算法

本文算法利用 Tucker分解方法将视频张量进行分解，然后提取时间维因子矩阵代表视频特征的主要成分，进行相关性计算。算法主要步骤如图3所示。

3.1 预处理

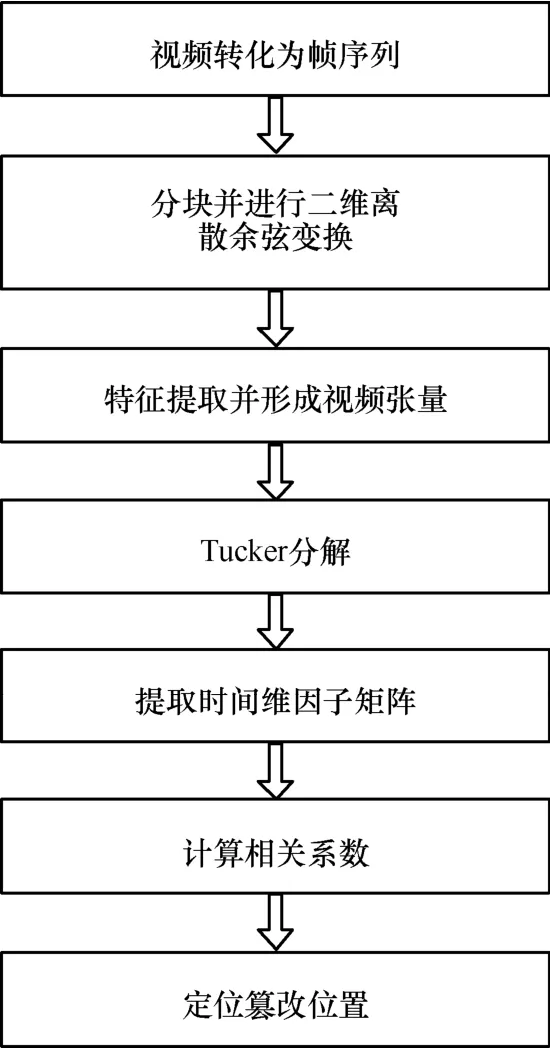
图3 检测算法流程

将待检测视频转换为帧序列，并对每帧图像进行灰度化处理。记录视频帧序列的长度为T。

3.2 特征提取

将每帧图像分为 B ×B的不重叠的块，利用离散余弦变换（DCT，discrete cosine transform）对视频帧进行压缩处理[10]，经过离散余弦变换的图像块的信息从均匀分布变换为不同密度分布，变换后的每个图像块都会产生与原图像块大小一致的系数矩阵。在矩阵中，图像的低频信息集中在左上角，高频信息集中在右下角，图像低频部分的信息量要大于高频部分的信息量，因此，本文取系数矩阵左上角的8× 8的系数形成新的特征矩阵F来表示图像块的内容。

对特征矩阵F进行量化。将矩阵F对应位置除以一个量化表Q，四舍五入取整，得到一个量化后的矩阵K。如图4所示，量化表Q中左上角的值按Z字形向右下角递增，使量化后的矩阵K左上角的值保持不变，右下角的值呈现能量递减。量化目的是抑制矩阵F右下角的高频分量，保持左上角的低频分量不变。

对量化后得到的矩阵K，同样采用图4的Z字形模式进行扫描数据，得到一个1× 64维的特征向量FeaV。在图像中，低频信息较高频信息更为重要，因此使用Z字形模式编码后，可以使特征向量每个数据的重要性由头至尾递减。

图4 Z字形模式编码

对于M × N大小的帧，有block_NUM个块，对于每个图像块，都会得到一个1× 64的特征向量，那么每帧图像都将产生一个 block_NUM×64的特征矩阵来表示该帧的内容。

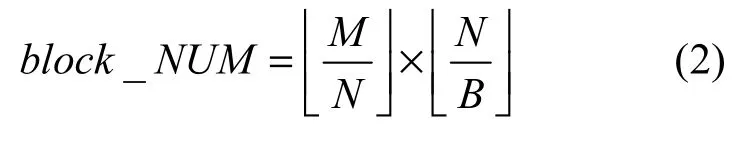
3.3 张量分解

经过特征提取后，每帧图像内容可以用一个特征矩阵来表示，对矩阵直接进行相关性计算，计算量大、算法复杂，因此本文使用可以对大量高维数据表达、操作且保持良好性能的张量方法来描述视频特征。将视频特征形成一个三维张量，若视频的长度为 T，每帧图像的特征矩阵大小为那么视频将形成一个大小为的三维张量R，对三维张量R进行分解，提取时间维的因子矩阵信息，该因子矩阵的每一行可视为每帧特征的主要成分。把计算相邻帧之间的相关性问题转换为计算相邻向量间的相似度问题。由于视频数据具有非负特性，所以本文使用非负张量分解，分解后的核心张量及各维度的因子矩阵均为非负值。

对于三维张量 RI×J×T（I为block_NUM，即每帧划分的图像块数量，J为64，T为视频的长度），本文使用交替最小二乘（ALS, alternating least squares）方法，融合所有其他矩阵去处理一个因子矩阵，重复过程直到收敛。当到达某一个最大迭代次数或因子矩阵改变很小的时候，结束算法。

输入 张量R，最大迭代次数T_max

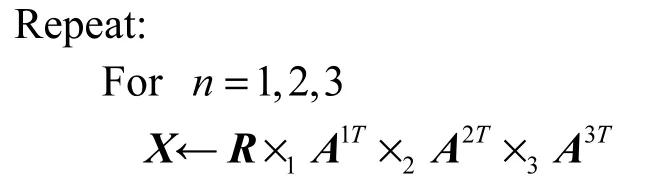
对X进行SVD分解，求得左奇异值向量An

End for

当迭代次数达到最大迭代次数T_max或因子矩阵变化很小时，停止迭代。

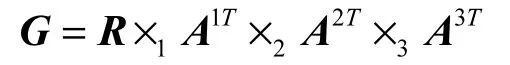
3.4 计算相关性

用时间维度的因子矩阵的每一行向量来表示每帧的内容，然后通过计算相邻向量的相关系数确定是否有帧的删除或插入篡改。本文使用Pearson相关系数用来衡量因子矩阵每个相邻向量之间的相关性。

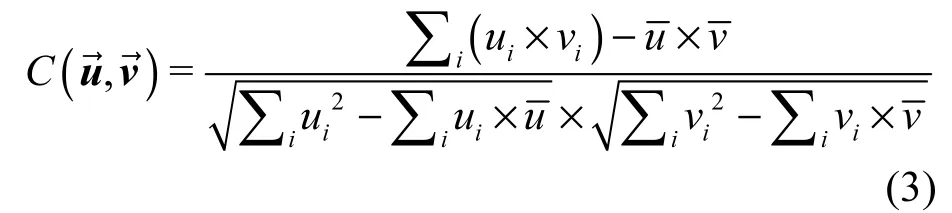
相关系数C的值介于−1与 1之间。当相关系数C趋近于1时，表示2个向量是极强相关的。若被检测视频未经篡改，相邻帧间应具有很强的相关性。当视频经过帧间篡改，篡改位置的帧间的相关性将被削弱，相关系数C会趋近于−1。

3.5 定位篡改位置

对于一个长度为T的视频张量，可以求得 T−1个相关系数C，将产生一个相关系数集合Cf。

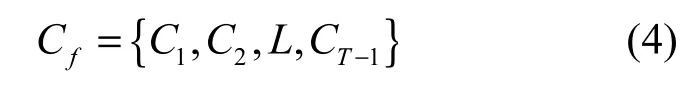
篡改位置时，帧间的相关性会减弱，相关系数会出现异常。为了定位篡改位置，需找到集合Cf中的异常点。本文使用切比雪夫不等式[11]定位异常点。

切比雪夫不等式证明，在随机数据中，每个数据到该数据集均值的距离都遵循一定的概率，这种概率与数据集的标准差有关。

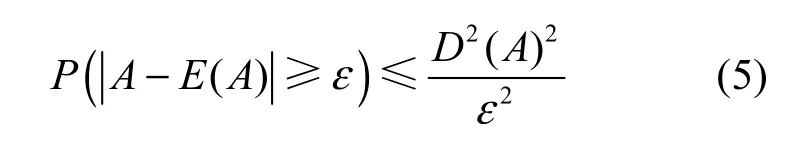
其中，E(A)为数据集合A的均值，D(A)为标准差，ε为标准差的整数倍。

由式(5)可以推导得到：

当 ε =3D(A)时，

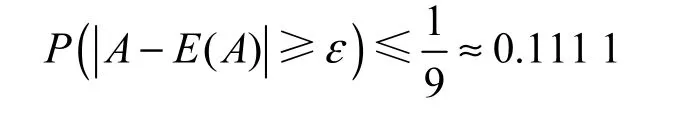
当 ε =4D(A)时，

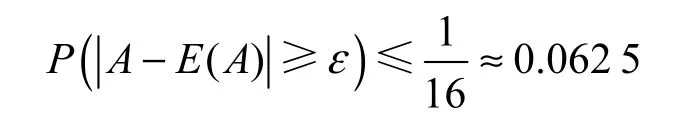
当 ε= 5D(A)时，

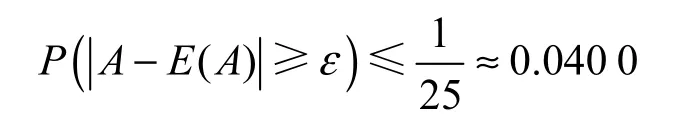
可以看出，在一个样本集合中，距离均值越远的数据点出现的概率越小，可以认为是数据样本中的离群点。因此，可以根据切比雪夫不等式，找出与数据集均值的距离大于ε的数据，认为该数据是异常点。使用切比雪夫不等式，可以根据每个数据集的分布特点，自适应地设定一个阈值，而无需人为设定阈值。

本文将ε的值设定为相关系数集合Cf的标准差D(Cf)的3倍，即在相关系数集合Cf中，若数据点到集合Cf的均值E(Cf)的距离大于阈值ε，如式(6)，则该数据点被认为是异常点。

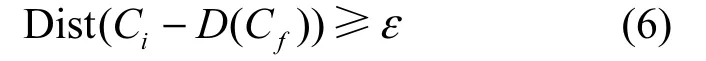
4 实验分析

本文用来进行实验的视频来自 Surrey University Library for Forensic Analysis (SULFA)[12]视频库和自己拍摄的视频，自己拍摄的视频使用 Canon EOS 6D 设备拍摄，视频分辨率有 3种，为1920× 1080、1280 × 720、640 × 480。使用Adobe Premiere Pro CC软件进行视频篡改，使用Matlab R2014b进行算法的实现，计算机配置为Intel Core i5-4590 CPU 3.30 GHz、8 GB内存、Windows 7系统。

本文对视频时域上的帧间篡改操作进行检测，分别有帧删除篡改、同源帧插入、异源视频帧插入这3种篡改方法。

针对异源视频帧插入篡改，插入的帧会与原始视频帧极不相似，如图5(a)所示，第28帧和第29帧之间的相关系数、第38帧和第39帧的相关系数会趋近−1，因为第 29～38帧为其他视频插入的帧，与原始视频帧不相似，相关系数会趋近于−1。对于插入同源视频帧的篡改，由于插入的帧来自待检测视频本身，因此具有一定的相似度，容易发生漏检现象，但相邻视频帧具有极强的相关性，被插入的帧与相邻帧的相似度会降低，如图5(b)所示，第12帧和第13帧之间的相关系数、第20帧和第21帧的相关系数与其他相关系数相比偏低。针对视频帧删除篡改，必须删除一定数量的帧才能达到有意义的篡改，本文实验采用删除20帧以上数量的帧的视频，经过帧删除篡改的视频，被篡改的位置会出现不连续的情况，该位置的相邻帧的相似度会降低，如图 5(c)所示，在 120帧位置进行了帧删除操作，因此120帧与121帧之间的相关系数会出现偏低的情况。

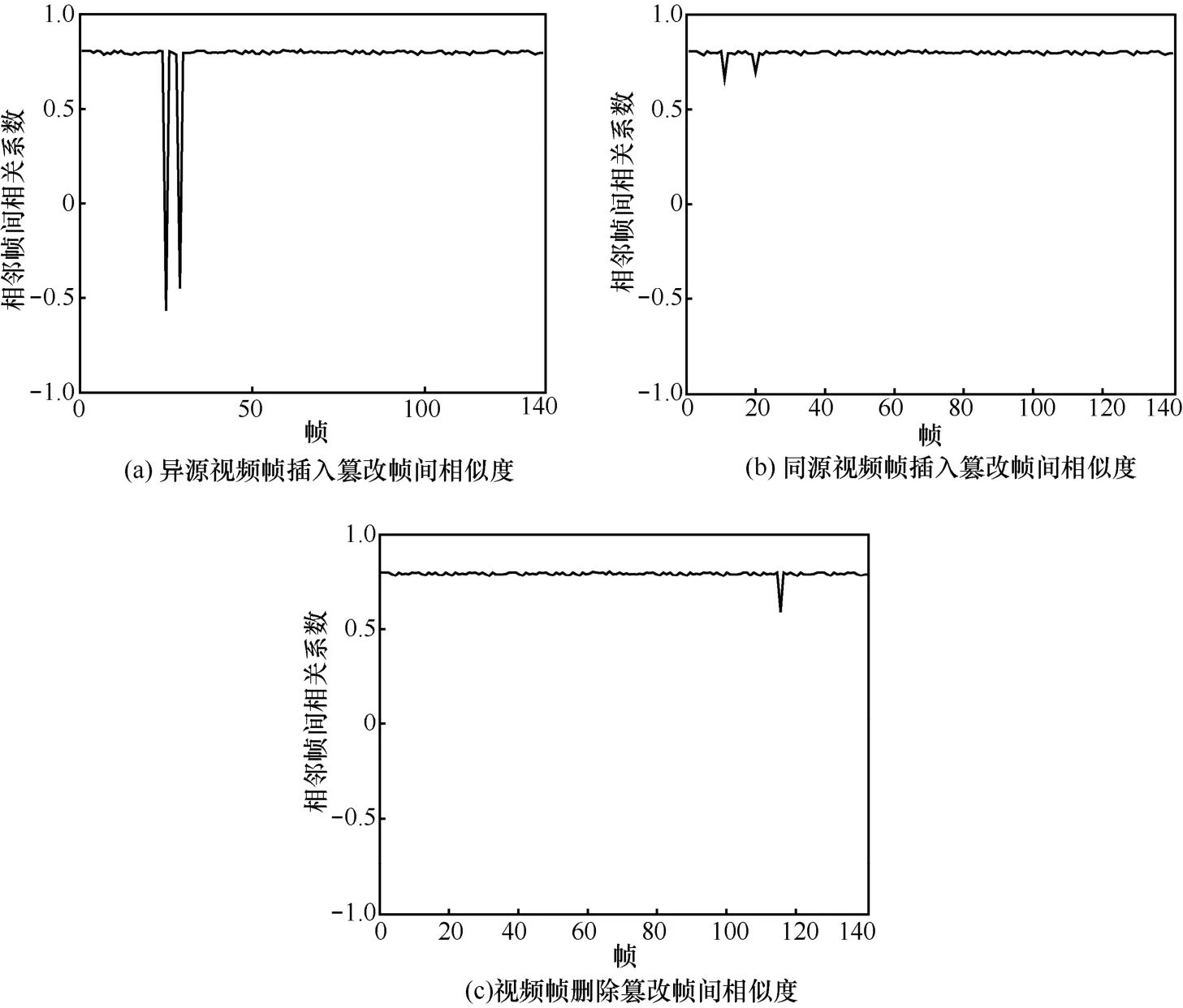
图5 视频相邻帧相关系数

为了评价算法的性能，本文使用准确率(precision)和召回率(recall)对实验结果进行分析。

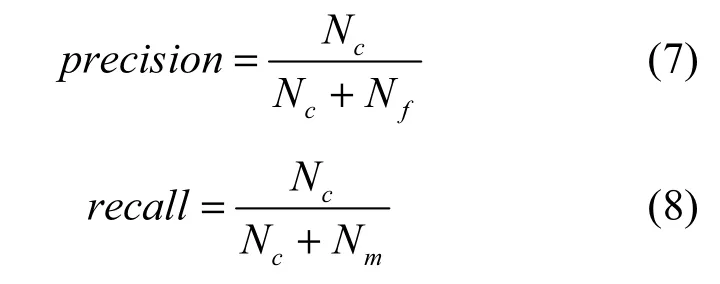
其中，Nc是算法正确检测出的帧的数量，Nf是错误检测的帧的数量，Nm是算法误认为是正常帧的篡改帧的数目，即漏检的帧的数量。

实验的具体结果如表1所示，平均每帧检测所需时间较短。本文算法与文献[5]的算法进行比较，文献[5]的实验视频均为异源视频插入篡改，且检测视频均为背景静止的视频。通过对比实验发现，文献[5]对于同源视频插入篡改检测的效果不够理想，且针对视频删除篡改检测的漏检较多。本文与文献[5]的不同篡改操作检测对比结果如表2～表4所示，本文算法的准确率和召回率均高于文献[5]。

5 结束语

本文提出一种基于非负张量分解的视频篡改检测方法，快速提取视频特征，并将其张量化，使每个视频可以用一个三维张量进行表示，然后对张量进行Tucker分解，提取时间维因子矩阵信息，代表视频特征的主要成分，利用视频相邻帧高度相似的原理，进行视频相邻帧相关系数的计算，寻找异常点，定位篡改位置。通过实验表明，本文算法能有效检测出视频时域上的帧插入和删除篡改，快速提取帧压缩特征与张量分解的结合方法大大提高了检测速度。不足之处在于帧删除篡改和同源视频帧插入篡改的检测仍存在一定的局限性，由于篡改后的视频帧之间仍可能存在高度相似性，容易造成漏检，这也是今后需要重点研究的工作。

表1 不同分辨率视频篡改检测结果

表2 异源视频帧插入篡改检测结果

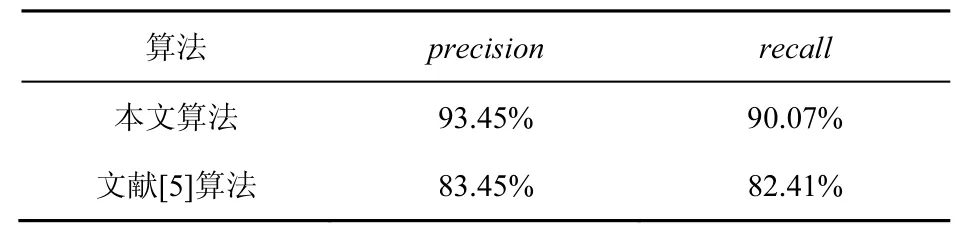
表3 同源视频帧插入篡改检测结果

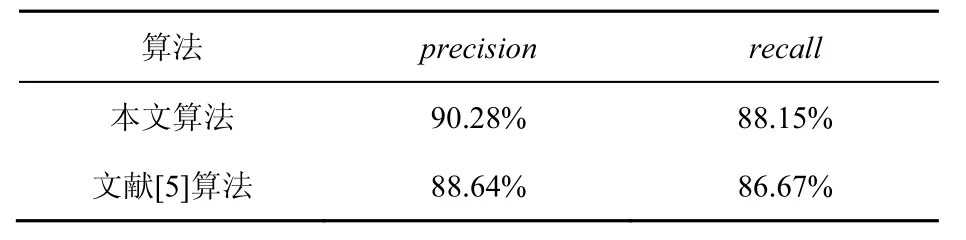
表4 视频帧删除篡改检测结果

[1] 胡永健, 刘琲贝, 贺前华. 数字多媒体取证技术综述[J]. 计算机应用, 2010, 30(3):657-662.

HU Y J, LIU B B, HE Q H. Review of digital multimedia forensics[J]. Journal of Computer Applications, 2010, 30(3):657-662.

[2] 王俊文, 刘光杰, 张湛, 等. 基于模式噪声的数字视频篡改取证[J].东南大学学报(自然科学版), 2008(S2):13-17.

WANG J W, LIU G J, ZHANG Z, et al. Digital video tampering with evidence based on modal noise[J]. Journal of Southeast University (Natural Science), 2008(S2):13-17.

[3] 袁秀娟, 黄添强, 陈智文, 等. 基于纹理特征的数字视频篡改检测[J]. 计算机系统应用, 2012, 21(6):91-95.

YUAN X J, HUANG T Q, CHEN Z W, et al. Digital video tamper detection based on texture feature[J]. Computer Systems & Applications, 2012, 21(6):91-95.

[4] 黄添强, 陈智文, 苏立超, 等. 利用内容连续性的数字视频篡改检测[J]. 南京大学学报(自然科学), 2011, 47(5):493-503.

HUANG T Q, ZHEN Z W, SULC, et al. Digital video tamper detection with Content continuity[J]. Journal of Nanjing University (Natural Science), 2011, 47(5):493-503.

[5] YIN L, BAI Z, YANG R. Video forgery detection based on nonnegative tensor factorization[C]//The 4th IEEE International Conference on Information Science and Technology(ICIST). 2014: 148-151.

[6] KOLDA T G, BADER B W. Tensor decompositions and applications[J]. SIAM Review, 2009,51(3):455-500.

[7] TUCKER L R. Some mathematical notes on three-mode factor analysis[J]. Psychometrika, 2006, 31(3):279-311.

[8] LATHAUWER L D, MOOR B D, VANDEWALLE J. A multilinear singular value decomposition[J]. Siam Journal on Matrix Analysis & Applications, 2000, 21(4):1253-1278.

[9] BADER B W, KOLDA T G. Algorithm 862: Matlab tensor classes for fast algorithm prototyping[J]. ACM Transactions on Mathemat-ical Software, 2006, 32(4):635-653.

[10] 林晶, 黄添强, 赖玥聪, 等. 采用量化离散余弦变换系数检测视频单帧连续多次复制-粘贴篡改[J]. 计算机应用, 2016, 36(5): 1356-1361.

LIN J, HUANG T Q, LAI Y C, et al. Detect a siagle frame video’s continuous copy and paste by using Quantitative discrete cosine transform coefficients[J]. Compute Application, 2016, 36(5): 1356-1361.

[11] 贺忠. 基于 Lip-切比雪夫方法的数据流异常检测分析[J]. 计算机系统应用, 2009, 18(10):61-64.

HE Z. The data flow anomaly detection analysis based on Lip-Chebyshev method[J]. Computer System Application, 2009, 18(10): 61-64.

[12] QADIR G, YAHAYA S, HO A T S. Surrey university library for forensic analysis(SULFA)of video content[C]//The 2012 IET Conference on Image Processing．2012: 1-6.

Video tamper detection method based on nonnegative tensor factorization

ZHANG Xue-li1,2, HUANG Tian-qiang1,2, LIN Jing3, HUANG Wei1,2

(1. Faculty of Software, Fujian Normal University, Fuzhou 350007, China; 2. Fujian Provincial Engineering Research Center of Big Data Analysis and Application, Fuzhou 350007, China; 3. School of Mathematics and Computer Science, Fujian Normal University, Fuzhou 350007, China)

The authenticity and integrity of video authentication is one of the important contents in information security field. A video tampering detection method based on non-negative tensor decomposition was proposed for video inter-frame tampering. First of all, spectral feature of video frame was extracted quickly. The video was described by a three-dimensional tensor which created by the main compression feature. The tensor was factorized by Tucker non-negative decomposition method and then the time dimension matrix was extracted to calculate correlation. Finally, the tampering position was determined by using the Chebyshev’s inequality. Experiments show that this method can detect the video inter-frame tampering quickly and robustly.

video tampering detection, nonnegative tensor factorization, Pearson correlation coefficient, discrete cosine transform, Chebyshev’s inequality

s: The National Natural Science Foundation of China (No.61070062, No.61502103), The Industry-University Cooperation Major Project of Fujian Province(No.2015H6007), The Science and Technology Program of Fuzhou (No.2014-G-76), The Program for New Century Excellent Talents in University of Fujian Province(No. JAI1038), The Science and Technology Department of Fujian Province K-Class Foundation Project (No.2011007), The Education Department of Fujian Province A-Class Foundation Project (No.JA10064), The Graduate Education Reform Project of Fujian Normal University(No.MY201414)

TP393

A

10.11959/j.issn.2096-109x.2017.00174

张雪莉（1993-），女，河南正阳人，福建师范大学硕士生，主要研究方向为信息安全、数字多媒体取证。

黄添强（1971-），男，福建仙游人，博士，福建师范大学教授，主要研究方向为机器学习、数字多媒体取证。

林晶（1992-），女，福建莆田人，福建师范大学硕士生，主要研究方向为信息安全、数字图像取证。

黄维（1994-），女，福建莆田人，福建师范大学硕士生，主要研究方向为信息安全、数字多媒体取证。

2017-01-25；

2017-03-15。通信作者：黄添强，fjhtq@fjnu.edu.cn

国家自然科学基金资助项目(No.61070062,No.61502103)；福建省高校产学合作科技重大基金资助项目(No.2015H6007)；福州市科技计划基金资助项目(No.2014-G-76)；福建省高等学校新世纪优秀人才支持基金资助项目(No.JAI1038)；福建省科学厅K类基金资助项目(No.2011007)；福建省教育厅A类基金资助项目(No.JA10064)；福建师范大学研究生教育改革研究基金资助项目(No.MY201414)