安全高效的可验证大型线性方程组求解外包计算方案

2017-07-05张兴兰刘祥

网络与信息安全学报 2017年6期

关键词：线性方程组方程组复杂度

张兴兰，刘祥

（北京工业大学信息学部，北京 100124）

安全高效的可验证大型线性方程组求解外包计算方案

张兴兰，刘祥

（北京工业大学信息学部，北京 100124）

针对目前大型线性方程组求解在外包计算中遇到的用户信息泄露、计算结果被篡改等问题，提出一种安全高效的可验证外包计算方案。通过随机置换和线性方程组的恒等变换，构造了新的具备相似解的线性方程组，避免了当前数据伪装方案易受求解公因式法攻击的问题，同时提高了客户端的验证效率，降低了空间复杂度。性能分析表明，该方案具有极高的效率。

云外包计算；解线性方程组；可验证性

1 引言

随着现代科学技术的不断发展，计算机网络正以不可思议的速度改变着人们的生产生活方式。云计算作为一种十分快捷、高效、共享的服务模式，正成为信息技术领域最热门的研究问题。云计算的出现极大缓解了在大型科学计算和工程代数运算中本地终端所承受的巨大压力，为一些受本地计算资源束缚而无法进行的大型计算任务提出了有效的解决方案。外包计算模式由此产生，它将本地无法处理的大型计算任务发送到有能力的云端，然后云端再将运算结果返回客户端。

外包计算虽然带来了诸多便利，但也存在一些安全隐患，如用户的数据隐私问题[1]。在外包计算过程中，当用户把数据上传至云端后，由于其底层计算过程对用户来说是不透明的，即云端的操作对用户来说是不可控的，因此，为了保护用户的数据安全，降低机要数据被恶意外泄的风险，需要对用户隐私数据进行加密处理[2]。目前，传统的数据加密方式并不能直接应用于云安全外包计算领域，是因为传统的加密方式虽然可以实现对数据隐私的保护，但同时也阻止了云端对底层数据进行任何有意义的操作。因此，目前安全外包计算依然是学术界重点关注的领域之一。

当前可用的安全外包技术方案主要是基于冗余策略、伪装技术和密码学的方法[3～7]。2001年，Atallah等[8～10]第一次研究了数值分析和科学计算问题的安全外包计算方案，提出了一系列适合于线性计算、排序、字符串模式匹配等不同科学应用问题的数据伪装技术。这些数据伪装技术虽然在一定程度上保护了用户数据的隐私性，但在数据隐藏的时候每一组系数都含有一个公共的因子，当攻击者使用提取公因子法攻击时，可以轻而易举地恢复出明文；另外，虽然在一定程度上实现了对数据隐私的保护，但并没有实现对云服务器计算结果进行正确性和可靠性验证，当攻击者返回一个错误结果时，用户并不能及时发现，且协议的效率不高，执行时存在多轮交互的通信开销。2011年，Payman[11]利用矩阵同态加密方案设计了基于线性代数的云外包计算协议，虽然该方案实现了对隐私数据的保护，但协议中采用同态加密方案产生的密文较长，需要较大的预计计算量，导致计算效率较低，也增加了通信的开销。2013年，胡杏等[12]利用系数矩阵逆的外包计算的方案实现了线性方程组解的外包计算，但该方案存在2个缺陷：1)将系数矩阵进行2次加密处理，然后发送云端求逆，降低了运算效率；2)在2次矩阵逆的外包计算过程中，需要将2个加密矩阵分别发送到服务器上，然后再由服务器将结果返回到客户端，这不仅增加了通信开销，同时也增加了存储开销。2015年，Chen等[13]同样利用数据伪装和矩阵的恒等变换构建了一个可验证的外包协议，但是该协议并没有提高用户输入数据的安全性，同时在验证时需要将解向量整体带入线性方程组，给客户端造成压力。2016年，蔡建兴等[14]基于克罗内克函数和随机置换算法提出了 2次通信的线性方程组的外包方案，该方案虽然降低了通信效率和空间存储复杂度，但并没有从根本上解决由于系数的每行（列）都存在公共的系数，攻击者利用提取公因子攻击可以很容易恢复出明文的问题；另外，该方案同样利用系数矩阵逆的方法求方程组的解，在结果验证时通过系数矩阵和其逆矩阵做乘法来判断其正确性，这大大增加了客户端的计算压力，使整个协议的执行效率受到极大影响。

本文在综合文献[8～14]优点和不足的基础上，采用冗余策略和数据伪装的思想[2,3]，通过扩充系数矩阵，构造一个与原线性方程组近似同解的新线性方程组。这样，既保证了原始系数规模和状态的安全性，同时又保护了解向量的安全性；且通过本文的计算方案，可以大大降低通信的传输效率和客户端结果验证的效率。本文与当前文献中主要利用系数矩阵的逆求解线性方程组不同，为求解线性方程组的外包计算提出了新思路。

2 外包计算模型

本文构建的外包计算模式如图1所示，是一个单云服务模型，接下来，分别从客户端和云端这2个方面介绍其主要工作流程。

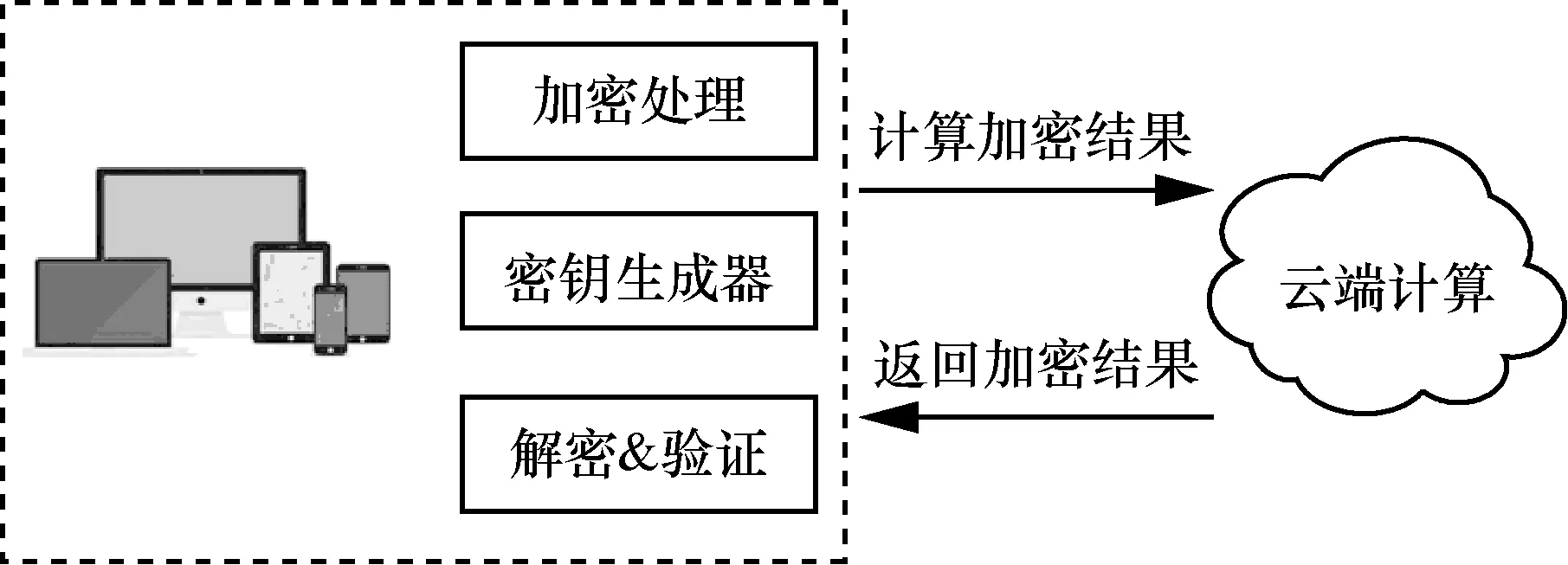
图1 外包计算模型

客户端：在客户端，用户的工作主要包括数据加密和数据解密验证这2个方面。在数据加密阶段，客户端利用密钥生成器，随机生成一个m t×随机矩阵 P，t阶对角矩阵Λ，以及t维随机解向量C。通过以上随机密钥值，构造一个新方程组，与原方程组相比，新方程组的解向量除了多添加的随机解向量C外，没有任何区别。然后，利用方程组的恒等变换和矩阵的可逆变换对增广矩阵进行处理，实现数据加密。在解密验证阶段，客户端通过逆变换将矩阵还原，然后找出解向量中添加的随机值，验证其是否正确，同时将原方程组的解向量随机代入方程组中的几个等式中，验证其正确性。

云服务器端：云服务器端的主要工作是根据用户发送的数据信息，如实地进行求解线性方程组的运算。客户端并不关心服务器以何种方式进行求解运算，只需要其能够返回运算结果，即线性方程组的解向量。

本协议面临的风险主要是来自云端的攻击行为，按照其攻击手段的差异，将其划分为半诚实模型和恶意模型。半诚实模型是指云端总会按照用户协议正确执行每一步操作，但可能会将用户数据泄露给存有恶意的第三方。恶意模型是指云端既不会严格按照用户协议正确地执行每一步操作，也不能保证其不会通过用户数据对原始数据或结果进行恶意推测、篡改等行为。为了保证方案的广泛适用性，本文所提协议主要针对恶意模型，因此必须满足以下几个方面。

1)正确性：如果云服务器能够按照协议的每一步正确执行，则其返回结果一定是正确的且一定能通过客户端验证。

2)安全性：攻击者不能从用户输入数据获取任何原始数据信息，也不能从计算结果推测出原始方程解的信息。

3)高效性：通过本文协议，客户端工作量远小于服务器的工作量，同时也远小于本地求解原始方程组的工作量。

4)可验证性：能够对服务器返回结果的正确性进行验证。通过验证的一定是正确的解；不能通过验证的解一定是错误的解。

3 安全外包计算协议

安全外包计算协议通过外包计算对线性方程组 Ax =B求其解向量

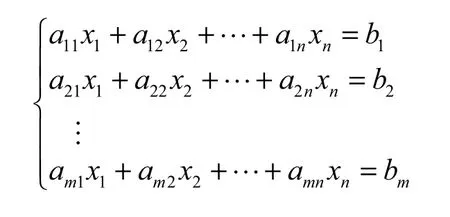
其中，

为结果矩阵。

3.1 置换函数和置换矩阵

本文引入组合论中随机置换函数π的概念，随机置换函数π可以用柯西两行式表示为

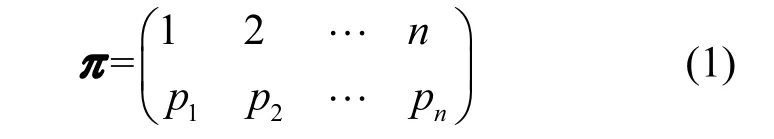
式(1)通过如下方式变换得到。

Step1 生成恒等置换函数

Step3 输出变换后的置换函数

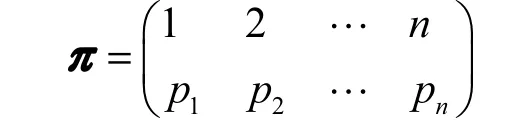
由上述随机置换函数的思想，结合矩阵论中置换矩阵的概念，即每行每列有且只有一个非零元 1。可以构造随机置换矩阵 Q，其中，

3.2 协议实现

大型线性方程组求解云外包计算协议 LP步骤如下。

Step2 客户端计算 C1=PC， C2=ΛC ，构造矩阵

Step3 生成2个m +t维随机置换函数π1、 π2和一个随机数集合K，对增广矩阵做如下变换得到矩阵

Step4 客户端生成 2个随机置换矩阵 Q1和其阶数分别为m +t和n + t，以及非零随机数λ，令

Step7 客户端验证。对 R1进行分块处理：

4 协议分析

本节从正确性、安全性、高效性和可验证性4个方面对上文提出的大型线性方程组求解云外包计算协议LP进行分析。

4.1 正确性

本协议满足正确性要求。根据协议 LP，可以得到，返回结果R一定是方程组的解。

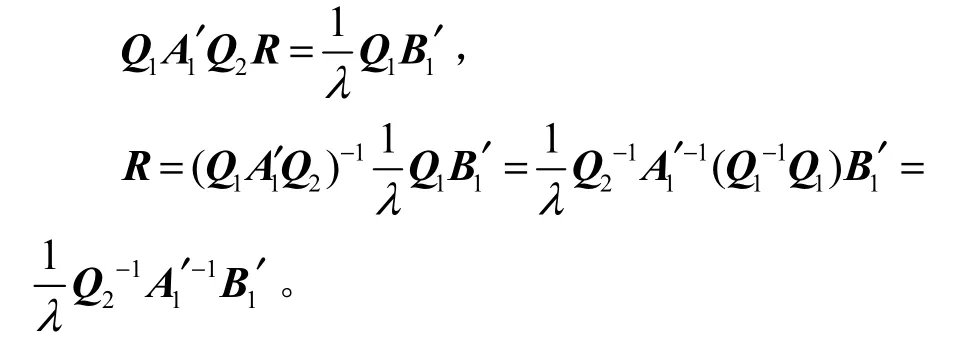
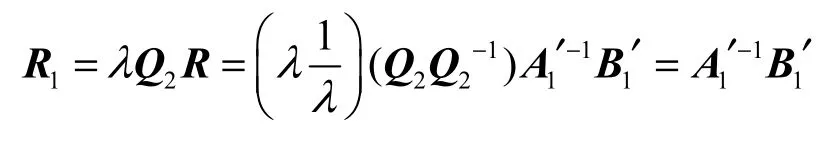
即 R1为方程组的解。

在Step3中，A1和 B1做的是等式的恒等变换，根据方程组的性质可知，方程组 A1x =B1一定与同解，即 R1也是方程组的解。

综上，该协议一定是正确的。

4.2 安全性

协议LP在恶意云模型中是可以安全运行的，接下来，从输入隐私数据的安全性和输出结果的安全性这2个方面进行分析。

输出安全性：输出安全性主要从2个方面进行分析，首先是服务器正确执行所有操作后，从输出结果推导出正确结果的概率；其次是服务器恶意返回错误的计算结果且通过客户端验证，被误认为正确结果接收的概率。

接下来，分析攻击者通过运算结果推出方程解的概率。服务器计算的结果R为方程的解，即

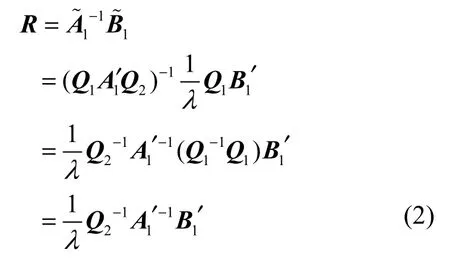
最后，分析攻击者返回错误的计算结果，而通过客户端验证被用户接受的概率。由于客户端对返回数据的验证是通过 2个方面进行的：首先验证返回的方程组解向量中特定位置的常数解和加密时添加的解是否完全一致，这需要从解向量中找出t个数；然后对其全排列，再乘以一个随机数λ，能正确恢复的概率是另外，客户端还需验证解向量是否满足方程组 Ax =B，一组错误的解同时满足方程组中t个随机等式的可能性是可以忽略不计的，所以，攻击者返回错误的计算结果，而被客户端接受的概率是可以忽略不计的。

综上，协议LP满足安全性的要求。

4.3 可验证性

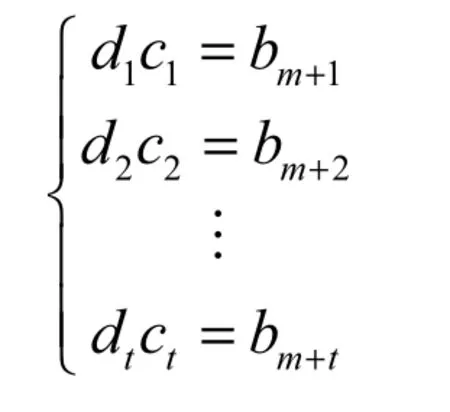
4.4 高效性

协议 LP具有高效性，以下从时间复杂度和空间复杂度2个方面对该协议进行分析。

从时间复杂度上来看，协议 LP的主要计算开销集中在数据伪装加密阶段。Step3中对数据进行恒等变换就是将其中一行系数的k倍加到其他行，其复杂度为Step4中对数据进行行列变换，就是将一整行或一整列整体移到其他行列，这样使用户数据和冗余数据充分融合，增加破译的难度，它的时间复杂度也是在数据验证阶段，其消耗只集中在将结果回代入方程组的k个等式中验证结果的正确性，其时间复杂度是综上，本协议中客户端的运算复杂度是若不采用外包计算，客户端直接进行解线性方程组的运算，最简单的方法就是利用矩阵的逆，直接求出系数矩阵的逆阵，其时间复杂度为然后再用系数矩阵的逆矩阵左乘结果矩阵得到线性方程组的解向量。所以，从时间复杂度上来看，本协议具备高效性。

从空间复杂度来看，协议LP主要的空间开销是保存2个随机置换矩阵 Q1和 Q2，已知置换矩阵每行每列有且只有一个非零元素1，所以可以考虑利用一维数组保存其每行非零元的位置，这样，其空间的复杂度为另一个开销是保存扩充的系数矩阵所占用的空间如果不进行数据外包，直接在本地进行计算，则需要计算出系数矩阵的逆矩阵，其所占用的空间为 O(m n)。因为t相对于矩阵的规模m和n来说，是一个很小的数，可以看出，通过外包计算的确能够增加客户端存储的复杂度，但增加的幅度并不是很大，是完全可以接受的。

综上，协议LP满足高效性。

5 实验分析

本节通过与相关文献[12～14]的对比分析和仿真实验对协议效率进行评估。

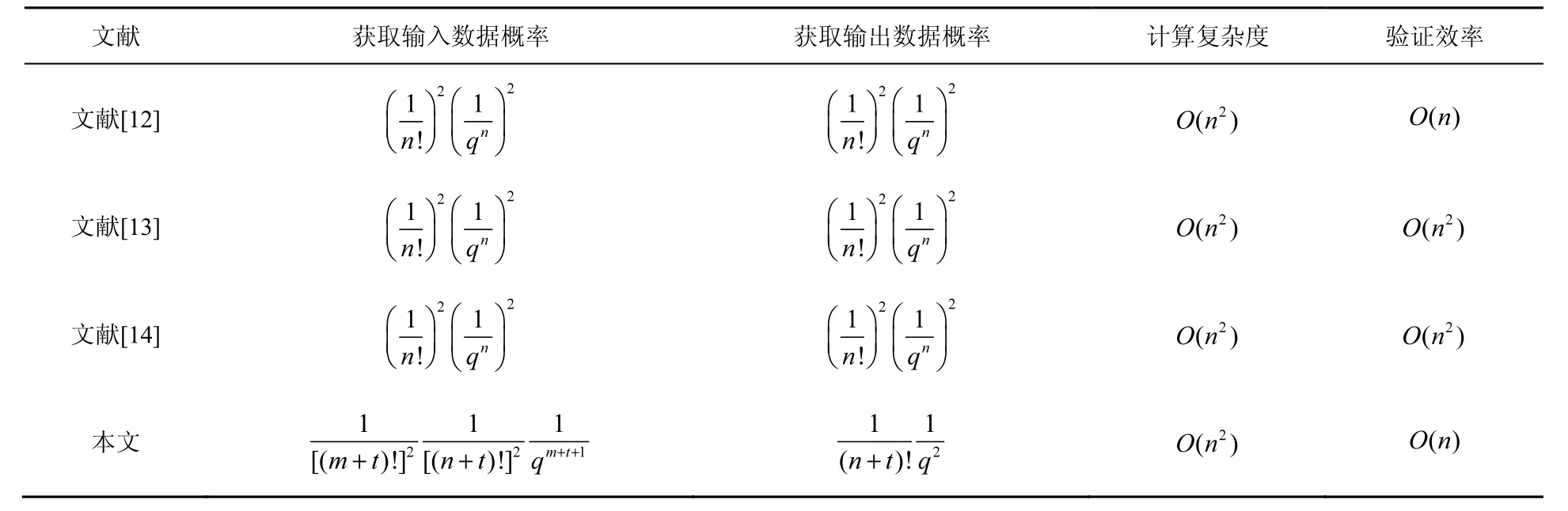
表1 本文协议与相关文献的协议性能比较

通过表1数据可以看出，虽然在输出数据的隐私性方面，该线性方程组外包计算协议 LP稍显逊色，但就所要面对的大型数据计算来说，也是足够抵御恶意攻击的。另外，本文所提协议LP在保证合理计算复杂度的基础上，具备较高的输入隐私性，同时降低了验证的效率。

接下来，通过数据仿真实验对协议性能进一步分析。本文采用通过Python的NUmpy科学计算数据库对协议进行实现，然后将其客户端和云端共同部署在Windows 7 64 bit双核、8 GB内存的终端上，这样，一方面保证了实验免受网络延时的影响，另一方面通过对比云端数据在本地的计算时效和原始数据的计算时效，可以分析外包方案LP对计算量的影响，令通过图2可以看到，随着矩阵规模的增大，云端计算时间快速增长，而客户端的计算时效保持在一个较低的水平，增长速度较平缓，说明本文所提线性方程组求解外包计算方案 LP能够有效降低客户端的计算复杂度。另外，虽然通过协议LP加密后的方程组规模有所增加，但云服务器端的计算效率与本机直接计算原始数据的效率相差并不大，说明通过外包协议并 LP没有过多地增加计算的复杂度。

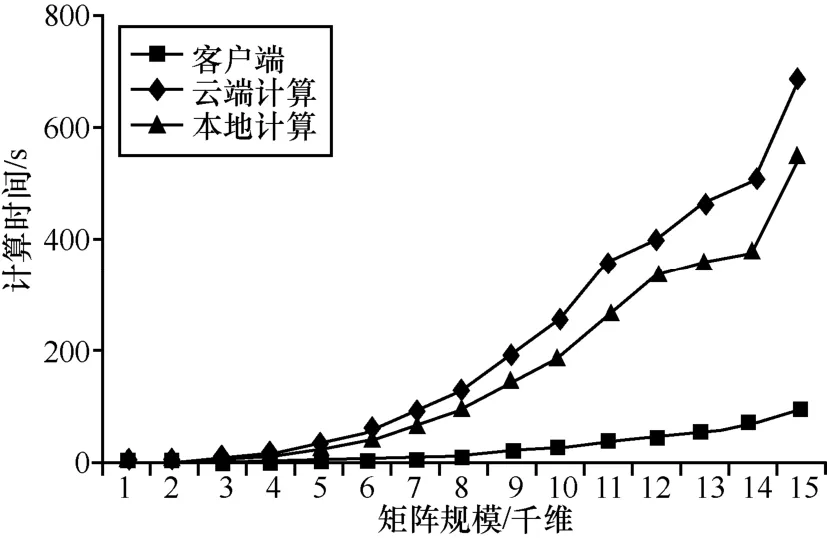
图2 协议执行效率折线

通过以上性能对比和仿真实验，该线性方程组求解外包计算协议LP在保证安全性的基础上，同时具备极高的效率。

6 结束语

本文利用随机置换和线性方程的恒等变换思想，构建了一个新的线性方程组求解的外包计算协议。该协议克服了原有外包计算方案中容易被求解公因子算法攻击的弊端，通过线性恒等变换，避免了公因子的存在；本文通过构建一个与原方程组解相似的新的方程组，将其进行外包计算，直接返回解向量，提高了客户端验证的效率，同时也降低了客户端的空间复杂度。该方案通过构造新的线性方程组，一改以往通过外包计算线性方程组系数矩阵逆的方法求解线性方程组，为线性方程组安全外包计算的研究提出了新思路。

[1] 冯登国, 张敏, 张妍, 等. 云计算安全研究[J]. 软件学报, 2011, 22(1): 71-83.

FENG D G, ZHANG M, ZHANG Y, et al. Study on cloud computing security[J]. Journal of Software, 2011, 22 (1):71-83.

[2] SHAMIR A. How to share a secret[J]. Communications of the ACM, 1979, 22(11):612-613.

[3] WANG C, REN K. Secure and practical outsourcing of linear programming in cloud computing[C]//IEEE Infocom. 2011:820-828.

[4] 任艳丽, 谷大武, 蔡建兴, 等. 隐私保护的可验证多元多项式外包计算方案[J]. 通信学报, 2015, 36(8): 23-30.

REN Y L, GU D W, CAI J X, et al. Verifiably private outsourcing scheme for multivariate polynomial evaluation[J]. Journal onCommunications, 2015, 36(8):23-30.

[5] WANG C, REN K, WANG J, et al. Harnessing the cloud for securely solving large-scale systems of linear equations[C]//The 31st International Conference on Distributed Computing Systems. 2011: 549-558.

[6] FIORE D, GENNARO R. Publicly verifiable delegation of large polynomials and matrix computations, with applications[C]//ACM Conference on Computer and Communications Security. 2012: 501-512.

[7] 邬国欣. 矩阵运算可验证安全外包计算协议的研究[D]. 西安:西安电子科技大学, 2014.

WU G X. On verifiable and secure outsourcing protocols for matrix operations[D]. Xi'an: Xidian University, 2014.

[8] ATALLAH M, FRIKKEN K. Securely outsourcing linear algebra computations[C]//ACM Symposium on Information, Computer and Communications Security. 2010:48-59.

[9] ATALLAH M J, PANTAZOPOULOS K N, RICE J R, et al. Secure outsourcing of scientific computations[J]. Adv Comput, 2001,54(1): 216-272.

[10] ATALLAH M J, FRIKKEN K. Securely outsourcing linear algebra computations[C]//The 5th ACM Symposium on Information, Computer and Communications Security. 2010: 48-59.

[11] PAYMAN M. Efficient and secure delegation of linear algebra[J]. IACR Cryptology Eprint Archive, 2011:1-33.

[12] 胡杏, 裴定一, 唐春明, 等. 可验证安全外包矩阵计算及其应用[J].中国科学: 信息科学, 2013, 43(7): 842-852.

HU X, PEI D Y, TANG C M, et al. Verifiable and secure outsourcing of matrix calculation and its application[J]. Scientia Sinca Informationis, 2013, 43(7): 842-852.

[13] CHEN X, HUANG X, LI J, et al. New algorithms for secure outsourcing of large-scale systems of linear equations[J]. IEEE Trans on Information Forensics and Security, 2015, 10(1): 69-78.

[14] 蔡建兴, 任艳丽. 大型线性方程组求解的可验证外包算法[J].计算机应用研究. 2017(2).

CAI J X, REN Y L. Verifiable outsourcing algorithm for large-scale systems of linear equations[J]. Application Research of Computers, 2017(2).

Secure efficient and verifiable large linear equations solve outsourcing computing scheme

ZHANG Xing-lan, LIU Xiang

(Faculty of Information Technology, Beijing University of Technology, Beijing 100124, China)

A secure, efficient and verifiable outsourcing computation scheme was proposed based on the current problems of leaking users information and tampering with the calculating results, which were encountered while solving large-scale linear equations in outsourcing computation. A new linear equation with similarity solutions was constructed based on the constant transformation between random permutation and linear equations. It avoids the problem that the current data camouflage scheme is easily attacked by solving common factor method. It also improves the verification effciency and reduces the complexity of space. The performance analysis shows that the scheme is highly efficient.

outsourcing cloud computing, solving linear equations, verifiability

The National Natural Science Foundation of China (No.61272044)

TP309.7

10.11959/j.issn.2096-109x.2017.00161