基于密码结构的扩散层构造

2017-07-05李鹏飞

网络与信息安全学报 2017年6期

关键词：二进制寄存器分支

李鹏飞

（1. 中国科学院信息工程研究所信息安全国家重点实验室，北京 100093；2. 中国科学院大学网络空间安全学院，北京 100049）

基于密码结构的扩散层构造

李鹏飞1,2

（1. 中国科学院信息工程研究所信息安全国家重点实验室，北京 100093；2. 中国科学院大学网络空间安全学院，北京 100049）

以分组密码扩散层为研究对象，根据轻量级分组密码的特点，基于2种密码结构构造轻量级扩散层，分别是基于Feistel结构构造面向软件实现的扩散层和基于LFSR构造面向硬件实现的扩散层。利用三轮Feistel结构，轮函数采用基于循环移位和异或的线性变换，构造出作用在8个4 bit和8 bit S盒上分支数为7的轻量级对合扩散层。基于LFSR构造出作用在4个4 bit和8 bit S盒上的次最优扩散层和作用在8个4 bit和8 bit S盒上分支数为7的扩散层。另外，利用LFSR构造出了6、7、8维MDBL矩阵以及16、18、32维分支数分别为7、7、12的大维数二进制矩阵。研究结果在分组密码的设计方面具有较高的应用价值。

分组密码；扩散层；Feistel结构；反馈移位寄存器；MDBL矩阵

1 引言

随着物联网（IoT，Internet of things）技术的快速发展，射频识别（RFID，radio frequency identification）标签、无线传感器网络（WSN，wireless sensor network）、个人数字助理（PDA，personal digital assistant）终端等微型嵌入式设备越来越发达，它们广泛应用于人们生活的方方面面，将任何物品与互联网连接起来，实现物与物、物与人、物与网络的信息交互，达到万物的智能化识别、定位、跟踪、监控和管理。然而，由于这些微型嵌入式设备只有有限的计算能力、通信能力、存储空间和能量来源，消耗更多软硬件资源、运行速度较差的传统密码算法（如DES[1]、AES[2]、SM4[3]等）已很难适用，给安全带来了极大的挑战，为了保障用户的数据和隐私安全，轻量级密码学应运而生，轻量级是相对于普通密码提供的安全保护级别和实现所需资源而言的，旨在安全性、面积功耗、时延速度等多个方面实现较好的折中。近几年，随着物联网的安全问题逐渐成为重要的研究课题，研究者相继提出了许多轻量级密码算法，包括轻量级分组密码、Hash函数、认证加密算法（如HIGHT[4]、PRESENT[5]、CLEFIA[6]、LED[7]、LBlock[8]、PRINCE[9]、SIMON和SPECK[10]、Zorro[11]、SIMECK[12]、PHOTON[13]、PRIMATEs[14]）等，这些算法的典型特点是：在严格规定的硬件资源条件下，能够达到一定的安全级别。

分组密码因其加解密速度快，便于软硬件实现和易于标准化等特点，成为轻量级密码学研究的重点，受到了学者的广泛关注。扩散层作为分组密码的一个重要部件，它的设计不但影响分组密码算法的安全性，而且影响分组密码在软硬件中的实现效率。一方面，扩散层为分组密码提供主要的扩散性，在抵抗差分分析和线性分析中扮演着重要的角色；另一方面，实现相同的安全性指标时，精心选择的扩散层可以显著提升分组密码算法在软硬件中的实现效率。目前，扩散层不仅是分组密码算法的必备部件，也在其他对称密码体制（如Hash函数、认证加密算法）中有广泛应用。扩散层的安全性能主要由文献[2]中提出的分支数的概念衡量，它是度量连续两轮差分和线性特征中活跃S盒数目下界的一个重要指标，利用它可以有效地计算差分特征概率和线性逼近概率的上界，估计密码算法的安全性。扩散层的分支数越小，分组密码越容易遭受差分分析、线性分析以及一些未知分析方法的攻击；反之，分支数越大，扩散层的扩散效果越好、安全性越好，因此，分组密码设计者面临的一大挑战是如何设计分支数大、软硬件实现代价低的扩散层，特别是在资源极端受限的物联网环境下。近几年，分组密码设计与改进的重点以及有所创新的地方主要集中在扩散层，有很多研究成果。

MDS（maximum distance separable）矩阵可以保证分支数达到最大，扩散性能达到最优，从而可以最大限度地保证密码算法在差分和线性分析下的安全性。许多密码算法都将 MDS矩阵作为扩散层使用，分组密码如 SHARK[15]、Rijndeal[2]、Twofish[16,17]、Square[18]、Anubis[19]、Khazad[20]、FOX[21]、CLEFIA、LED等，流密码如MUGI[22]，Hash函数如Maelstrom[23]，Grøstl[24]，WHIRLPOOL[25]和PHOTON轻量级Hash函数族[13]等。尽管这么多算法的扩散层都采用 MDS矩阵，但不可否认，MDS矩阵在提供最优扩散性的同时，也使算法的效率有所降低，它们通常需要较长的执行时间，消耗更多的软硬件资源，例如，硬件实现AES所需的最少电路门数为2 400等效门数[26]（GE，gate equivalents），其中仅列混淆部分就需要263 GE。关于MDS矩阵的研究也有很多[27～39]，这些MDS矩阵主要面向硬件实现，所需的异或个数极少，但没有过多地考虑软件实现效率。

分组密码算法设计中还经常采用 MDBL（maximum distance binary linear）矩阵作为扩散层使用，如ARIA[40]、Camellia[41]、E2[42]、MIBS[43]、Midori[44]、FIDES[45]、Minalpher[46]等密码算法中的扩散层都是使用MDBL矩阵，MDBL矩阵是二进制矩阵中具有最大分支数的矩阵[47]，它们相对MDS矩阵而言具有较高的软硬件实现效率，实现过程只需要异或操作，大大降低了软硬件资源消耗。表1给出了一些采用MDBL矩阵作为扩散层使用的密码算法。

相对于MDS矩阵，关于MDBL矩阵的研究比较少[48,49]，Kang等[50]证明了可逆8 × 8二进制矩阵的分支数小于等于5，即具有分支数5的8× 8二进制矩阵是最优的。Kwon等[40]证明了可逆16× 16二进制矩阵的最大分支数为 8，同时构造了许多分支数为8的16× 16对合二进制矩阵，并且使用一些数学方法找到了矩阵乘积的形式，使二进制矩阵在8 bit和32 bit处理器上软件的实现效率大大提高。

表1 一些采用MDBL矩阵作为扩散层的密码算法

Kanda等[51]通过搜索所有候选矩阵找到10 080个具有分支数5的8× 8二进制矩阵，这些矩阵的汉明重量均为44，其中，4个列（行）向量的汉明重量为6，另外4个列（行）向量的汉明重量为5，这些结果对E2和Camellia算法扩散层的设计具有一定的指导意义。

文献[52]提出了一种统一化的方法构造所有具有最大分支数5的8×8二进制矩阵，并且总结了它们的特征，发现这些矩阵的汉明重量集中在33～44。文献[53,54]采用组合小矩阵的方式构造大维数的二进制矩阵（16× 16或32 × 32矩阵）。文献[55]基于4× 4的 Hadamard矩阵和循环矩阵构造带有一个固定点并且分支数为7的16× 16二进制矩阵。

关于MDBL矩阵的研究，研究者很少提及二进制矩阵的软硬件实现，Dehnavi等[56]提出一种特殊类型（按位异或）的线性变换，这些线性变换可以表示成具有最大分支数的二进制矩阵的形式，可以有效地在软硬件上实现。

Feistel和线性反馈移位寄存器（LFSR，linear feedback shift register）是2种重要的密码结构。Feistel结构不仅广泛应用于对称密码算法（如DES、LBlock、SIMON和SIMECK）中，而且也被用来构造密码算法的关键部件——S盒和扩散层，如CRYPTON算法[57]、ZUC[58]、CS-Cipher[59]均采用三轮Feistel结构构造S盒，MISTY[60]算法也使用三轮Feistel结构构造它的非线性部分FI，文献[61]对三轮Feistel结构构造的S盒做了进一步研究，文献[62]使用三轮Feistel结构和MISTY结构构造轻量级S盒。同时，文献[63]研究了利用Feistel结构构造最优二进制矩阵，其轮函数采用比特置换。

对称密码中的流密码广泛应用于信息加密、分布式计算、码分多址（CDMA，code division multiple access）系统等领域。流密码技术的核心是构造性能优良的密钥流，线性反馈移位寄存器是一种基本的密钥流生成器，由于采用逻辑运算，具有原理简单、计算速度快、便于硬件实现等优点，成为构造密钥流生成器的重要部件之一[64]。正是由于LFSR的诸多优点，有学者将LFSR应用于分组密码扩散层的构造上，文献[7,16,29,30]设计的迭代型扩散层中就用到了LFSR。

本文结合Feistel和LFSR这2种密码结构的优势，将其用来构造分组密码的扩散层，首先研究了基于Feistel结构构造轻量级扩散层，轮函数采用基于循环移位和异或的线性变换，利用三轮Feistel结构构造出了作用在8个4 bit和8 bit S盒上的分支数为 7的轻量级对合扩散层；接着研究了基于LFSR构造轻量级扩散层，使用LFSR构造出了作用在n个m比特S盒上（ n= 4,8;m= 4,8）的轻量级扩散层和6、7、8维MDBL矩阵以及分支数分别为7、7、12的16、18、32维二进制矩阵。

2 预备知识

本节给出分支数的定义和 Feistel结构以及LFSR的基础知识。

2.1 分支数

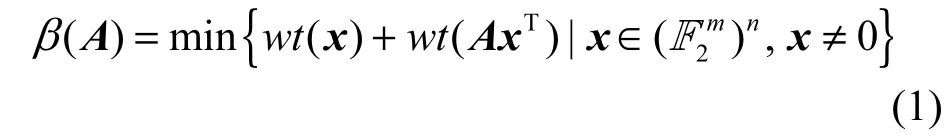
也称为扩散层θ的分支数，其中 wt(x)表示 x中非零分量的个数。

由定义1可知，扩散层的分支数 β≤ n+1。

定义2 将分支数达到最大(n + 1)时的扩散层称为最优扩散层，对应的矩阵称为MDS矩阵，其中，

定义3 将分支数达到次最大n时的扩散层称为次最优扩散层，对应的矩阵称为次MDS矩阵，其中，

2.2 Feistel结构

Feistel结构[65]广泛应用于对称密码算法中，许多分组密码算法都采用Feistel结构，其中最著名的是由IBM公司在20世纪70年代设计的DES算法。图1给出了Feistel密码结构的加解密过程。加密算法的输入是长度为2wbit的明文分组和用户密钥K，明文分组被分为等长（w bit）的两部分： LE0和 RE0，这两部分数据经过n轮迭代后组合成密文分组，第i轮迭代的输入 LEi−1和 REi−1来自于上一轮迭代的输出，第i轮迭代的轮密钥Ki是由用户密钥K推导出来的，一般地， Ki不同于K，并且 Ki之间也互不相同。

Feistel密码结构代替操作作用在数据的左半部分，整个结构通过将轮函数F作用于数据的右半部分后，与左半部分数据进行异或完成。Feistel结构每轮迭代都有相同的轮变换，但每轮的轮密钥 Ki不同，也就是说，轮函数F是w bit长的右半分组数据以及y bit长的轮密钥函数，第i轮轮函数的输出为w bit长的值轮函数操作后，与左半部分数据异或得到第 i+1轮右半部分数据 REi，第 i+1轮的左半部分数据 LEi是第 i轮的右半部分数据。在最后一轮迭代之后有一个交换，用以抵消在最后一轮迭代中的左右部分数据的交换。

Feistel密码结构的解密过程本质上和加密过程一致，其规则如下：将密文作为算法的输入，但逆序使用轮密钥 Ki，也就是说，第一轮使用Kn，第二轮使用 Kn−1，直到最后一轮使用 K1。基于以上特点，Feistel结构只需实现一个算法便可以完成加密和解密操作，大大简化了硬件实现的电路和软件实现的代码量。

2.3 LFSR

反馈移位寄存器由两部分组成：移位寄存器和反馈函数，移位寄存器是一个比特序列，它的长度用比特表示，若移位寄存器的长度为n bit，则称为n级移位寄存器。图2给出了二元域 GF(2)上的n级反馈移位寄存器，其中，n个寄存器从右至左依次称为第1,2,… ,n级。为反馈函数，它是 n个变量的布尔函数n级反馈移位寄存器的工作原理是：当一个时钟脉冲到来时，第i级寄存器的内容传送给第 i−1级寄存器第1级寄存器的内容为反馈移位寄存器的输出。反馈函数的值传送给第n级寄存器，可以看出，第 n级寄存器的值是根据其他寄存器的值计算得到的。反馈移位寄存器的输出序列（称为反馈移位寄存器序列）为

定义5 如果一个n级反馈移位寄存器的反馈函数是线性函数

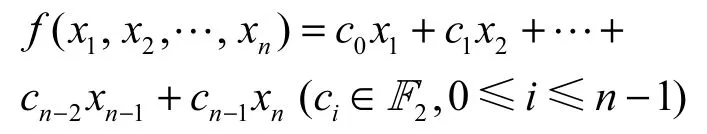
则称该反馈移位寄存器为线性反馈移位寄存器，输出序列称为线性反馈移位寄存器序列，记为LFSR序列。LFSR只有一种运算：异或运算，系数不全为0，若c0≠ 0,则称LFSR为非退化的，若 c0= 0,则称为退化的 LFSR。图 3给出了n级LFSR的结构图。

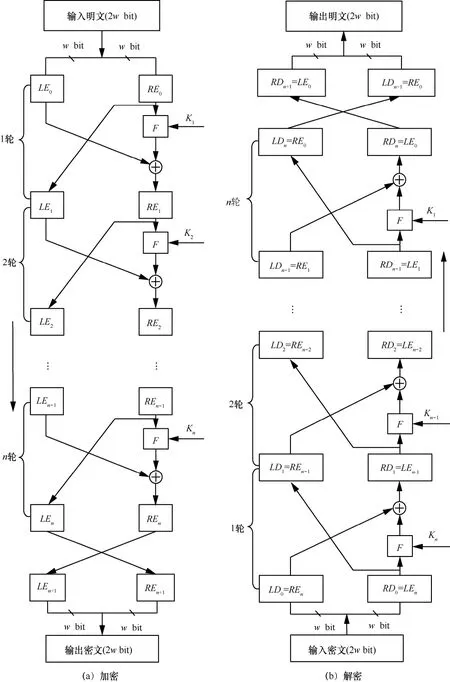
图1 Feistel密码结构加解密过程

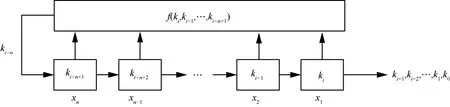
图2 反馈移位寄存器基本结构

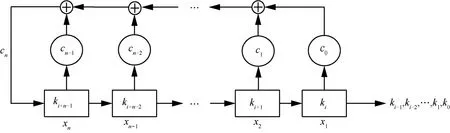
图3 n级LFSR结构

n级 LFSR可以由它的状态转移矩阵唯一表示，n级LFSR矩阵可以由状态转移矩阵的n次方计算得到，n级LFSR的状态转移矩阵如下。

其中， βn−1βn−2βn−3βn−4βn−5βn−6…β0为i的二进制表示，即 (i)2=βn−1βn−2βn−3βn−4βn−5βn−6…β0。

3 基于Feistel结构构造扩散层

本节使用三轮Feistel结构构造分组密码的扩散层，并且主要集中在对合扩散层的构造上。假设其中（m是S盒的比特长度，n是S盒的个数），基于Feistel结构的扩散层如图4所示，这类扩散层可以由矩阵表示为

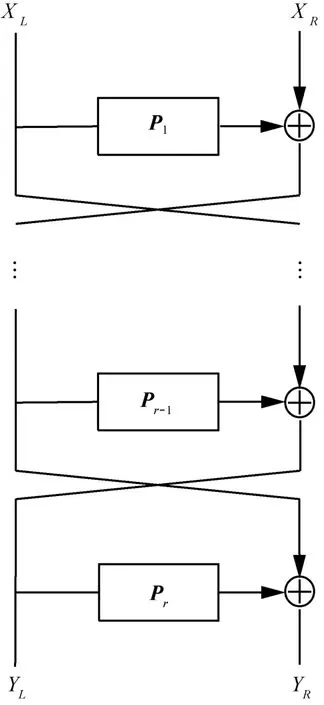
图4 r轮Feistel结构构造的扩散层

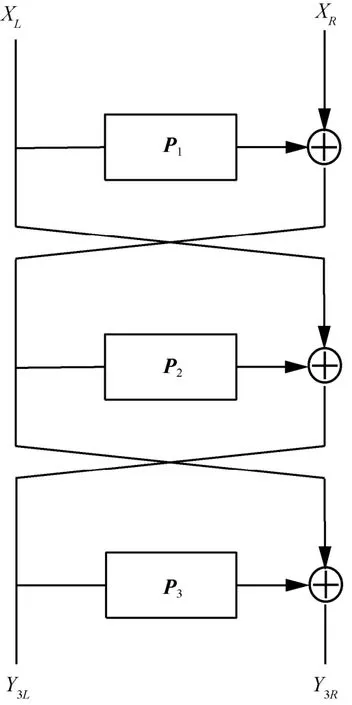
图5 三轮Feistel结构构造的扩散层

基于 Feistel结构构造轻量级扩散层的特点如下。一方面，基于Feistel结构构造的扩散层逆变换和其本身具有相同的结构，只需简单地按顺序反向使用轮函数即可实现逆变换。这种结构使扩散层和它的逆变换拥有相同的异或数，特别地，对合的扩散层可以使用相同的代码和电路实现加密和解密，大大节省了软硬件资源，当轮函数是对称的时候，矩阵 M为对合矩阵，如和另一方面，Feistel结构简单，它实际上是利用小矩阵构造大矩阵，如果采用简单的轮函数，将会构造出十分容易实现的扩散层。为了构造出既安全又高效的扩散层，限定采用三轮Feistel结构，并且只搜索对合扩散层。图 5给出了三轮 Feistel结构构造的扩散层，矩阵逆矩阵为对合扩散层要求轮函数 P1和 P3相同。下面给出作用在上的基于三轮 Feistel结构构造的轻量级对合扩散层。

本节研究使用循环移位和异或线性变换作为三轮Feistel的轮函数构造轻量级对合扩散层。基于 (Fm)n上的循环移位和异或运算的线性变换

2构造作用在上的扩散层即轮变换为基于循环移位和异或运算的线性变换：共含有k项，并且0 ≤ bj≤为了节省软硬件实现开销，利用3项及以下的基于循环移位和异或运算的线性变换构造分组密码的扩散层，即1 ≤ k≤ 3,并且只考虑对合扩散层。由于实际密码算法中8个4 bit和8 bit的S盒比较常见，所以这里令 n=4;对合扩散层矩阵为为简便起见，令轮变换为

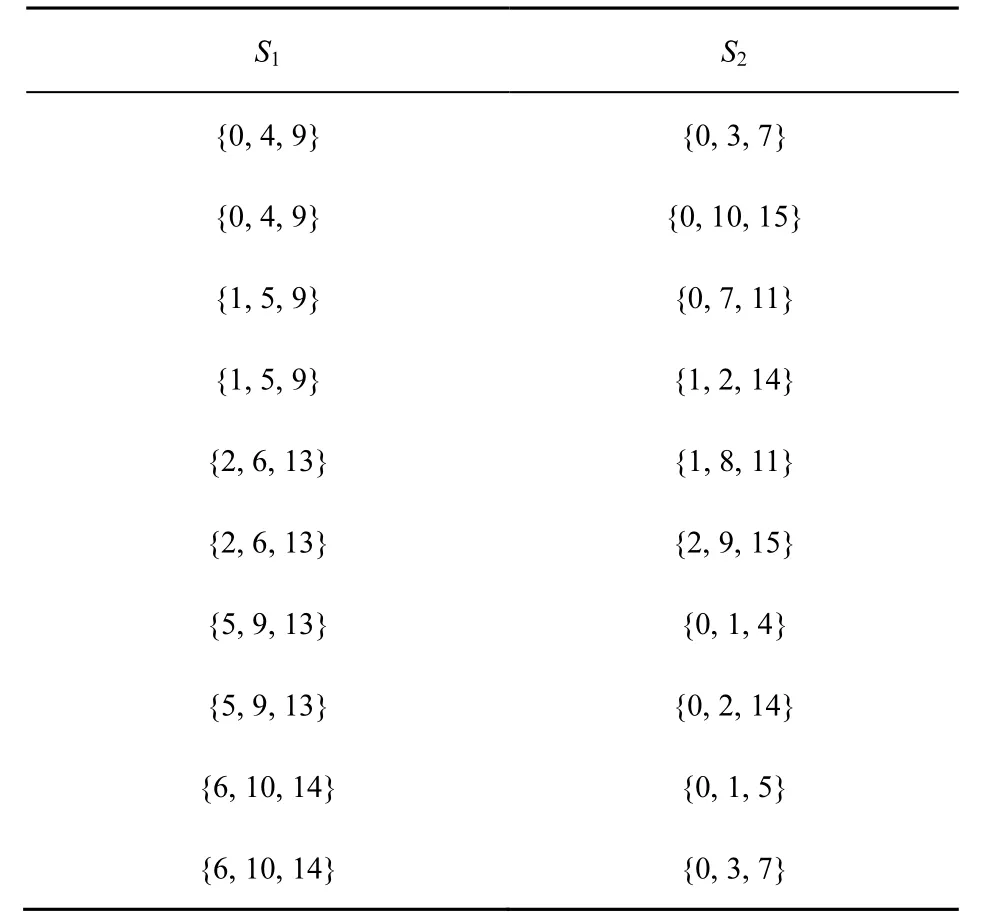
表2上构造分支数为7的对合扩散层L(X)

S1S2{ 0 , 4 , 9 } { 0 , 3 , 7 } { 0 , 4 , 9 } { 0 , 1 0 , 1 5 } { 1 , 5 , 9 } { 0 , 7 , 1 1 } { 1 , 5 , 9 } { 1 , 2 , 1 4 } { 2 , 6 , 1 3 } { 1 , 8 , 1 1 } { 2 , 6 , 1 3 } { 2 , 9 , 1 5 } { 5 , 9 , 1 3 } { 0 , 1 , 4 } { 5 , 9 , 1 3 } { 0 , 2 , 1 4 } { 6 , 1 0 , 1 4 } { 0 , 1 , 5 } { 6 , 1 0 , 1 4 } { 0 , 3 , 7 }

当n=4,m=8时，搜索了部分三轮Feistel结构构造的可逆扩散层，并且轮函数采用3项及以下的循环移位和异或运算的线性变换，没有找到MDS矩阵，找到部分作用在上的分支数为7的对合扩散层，表3给出了部分分支数为7的对合扩散层 L(X )的例子。

表3上构造分支数为7的对合扩散层L(X)

S1S2{ 6 , 1 4 , 2 2 } { 6 , 1 4 , 2 3 } { 6 , 1 4 , 2 2 } { 6 , 1 4 , 2 5 } { 6 , 1 4 , 2 2 } { 6 , 1 4 , 2 7 } { 6 , 1 4 , 2 3 } { 8 , 1 3 , 2 8 } { 6 , 1 4 , 2 3 } { 8 , 1 3 , 3 0 } { 6 , 2 1 , 2 9 } { 6 , 1 3 , 2 9 } { 6 , 2 1 , 2 9 } { 6 , 1 3 , 3 1 } { 6 , 2 1 , 2 9 } { 6 , 1 4 , 1 7 } { 6 , 2 2 , 3 0 } { 6 , 1 4 , 1 5 } { 6 , 2 2 , 3 0 } { 2 3 , 2 4 , 3 1 } { 6 , 2 2 , 3 0 } { 2 3 , 2 5 , 3 1 }

4 基于LFSR构造扩散层

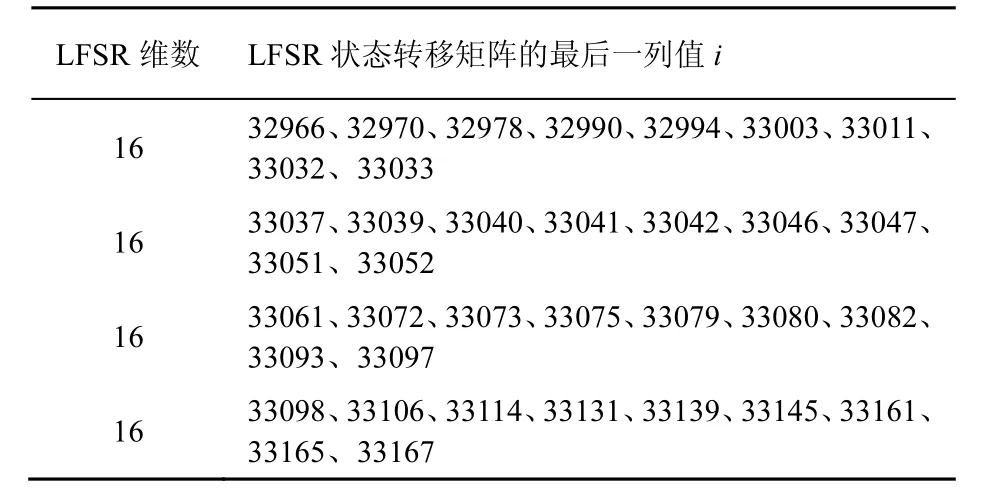
表4 利用LFSR构造出上的次最优扩散层

L F S R维数 L F S R状态转移矩阵的最后一列值i 1 6 3 2 9 6 6、3 2 9 7 0、3 2 9 7 8、3 2 9 9 0、3 2 9 9 4、3 3 0 0 3、3 3 0 1 1、3 3 0 3 2、3 3 0 3 3 1 6 3 3 0 3 7、3 3 0 3 9、3 3 0 4 0、3 3 0 4 1、3 3 0 4 2、3 3 0 4 6、3 3 0 4 7、3 3 0 5 1、3 3 0 5 2 1 6 3 3 0 6 1、3 3 0 7 2、3 3 0 7 3、3 3 0 7 5、3 3 0 7 9、3 3 0 8 0、3 3 0 8 2、3 3 0 9 3、3 3 0 9 7 1 6 3 3 0 9 8、3 3 1 0 6、3 3 1 1 4、3 3 1 3 1、3 3 1 3 9、3 3 1 4 5、3 3 1 6 1、3 3 1 6 5、3 3 1 6 7

表5 利用LFSR构造出上的次最优扩散层

LFSR维数 LFSR状态转移矩阵的最后一列值i 32 2147520533、2147520538、2147520547、2147520551、2147520562 32 2147520565、2147520571、2147520574、2147520578、2147520587 32 2147520590、2147520593、2147520598、2147520599、2147520619 32 2147520630、2147520631、2147520634、2147520642、2147520650

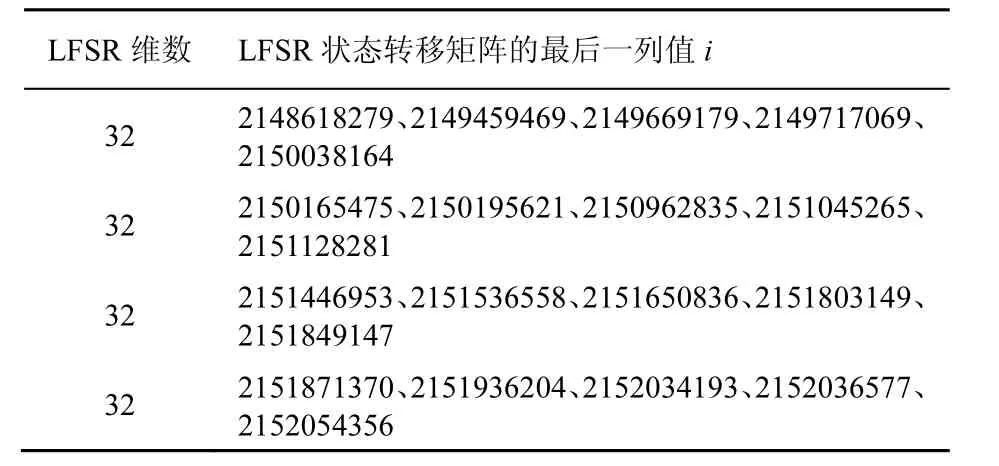
表6 利用LFSR构造出上分支数为7的扩散层

L F S R维数 L F S R状态转移矩阵的最后一列值i 3 2 2 1 4 8 6 1 8 2 7 9、2 1 4 9 4 5 9 4 6 9、2 1 4 9 6 6 9 1 7 9、2 1 4 9 7 1 7 0 6 9、2 1 5 0 0 3 8 1 6 4 3 2 2 1 5 0 1 6 5 4 7 5、2 1 5 0 1 9 5 6 2 1、2 1 5 0 9 6 2 8 3 5、2 1 5 1 0 4 5 2 6 5、2 1 5 1 1 2 8 2 8 1 3 2 2 1 5 1 4 4 6 9 5 3、2 1 5 1 5 3 6 5 5 8、2 1 5 1 6 5 0 8 3 6、2 1 5 1 8 0 3 1 4 9、2 1 5 1 8 4 9 1 4 7 3 2 2 1 5 1 8 7 1 3 7 0、2 1 5 1 9 3 6 2 0 4、2 1 5 2 0 3 4 1 9 3、2 1 5 2 0 3 6 5 7 7、2 1 5 2 0 5 4 3 5 6

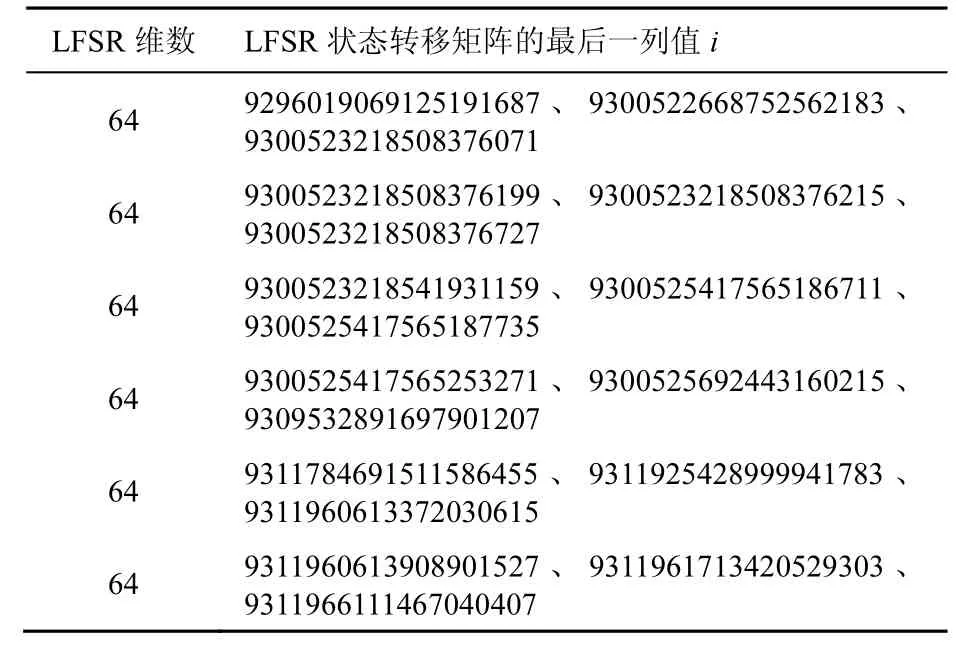
表7 利用LFSR构造出上分支数为7的扩散层

LFSR维数 LFSR状态转移矩阵的最后一列值i 64 9296019069125191687、9300522668752562183、9300523218508376071 64 9300523218508376199、9300523218508376215、9300523218508376727 64 9300523218541931159、9300525417565186711、9300525417565187735 64 9300525417565253271、9300525692443160215、9309532891697901207 64 9311784691511586455、9311925428999941783、9311960613372030615 64 9311960613908901527、9311961713420529303、9311966111467040407

4.2 构造二进制矩阵

二进制矩阵因为具有结构简单、实现过程只需要异或操作等优点，被广泛应用于分组密码算法中，MDBL矩阵是二进制矩阵中具有最大分支数的矩阵，很多密码算法，如ARIA、Camellia、E2、MIBS、Midori、FIDES、Minalpher等的扩散层都使用MDBL矩阵。本节讨论了基于n维LFSR构造作用在上n × n大小的二进制矩阵 Mn，这里m是S盒的比特长度，n是S盒的个数。

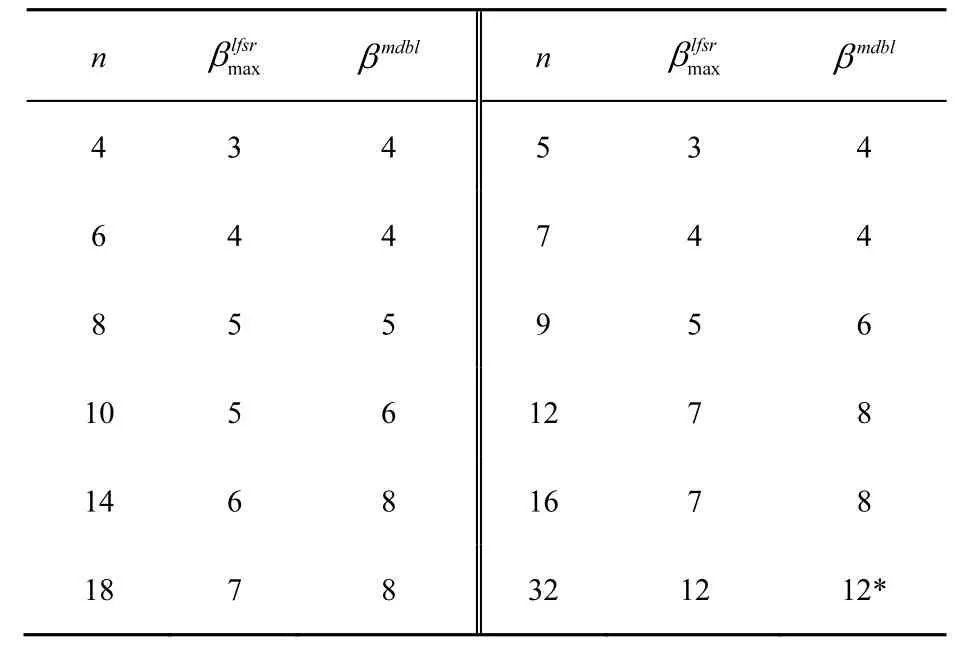
表8 n维LFSR矩阵最大分支数和MDBL矩阵的分支数 βmdbl

nmaxβlfsrβ nmaxmdblβ βmdbllfsr 4 3 4 5 3 4 6 4 4 7 4 4 8 5 5 9 5 6 10 5 6 12 7 8 14 6 8 16 7 8 18 7 8 32 12 12*

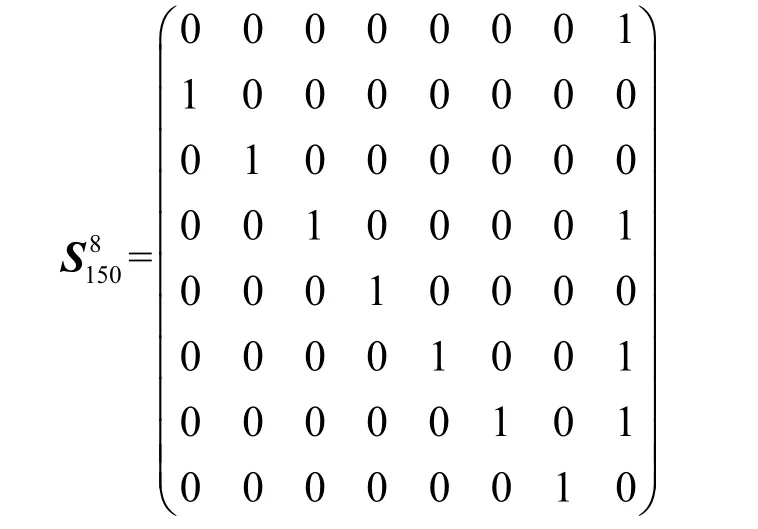
表 9统计了当矩阵维数为6,7,8时，利用 n维LFSR构造出的MDBL矩阵。表9中的为n维LFSR的状态转移矩阵，的n次方表示对应的MDBL矩阵 Mn，即

表9 当n=6,7,8时，利用LFSR构造出的MDBL矩阵

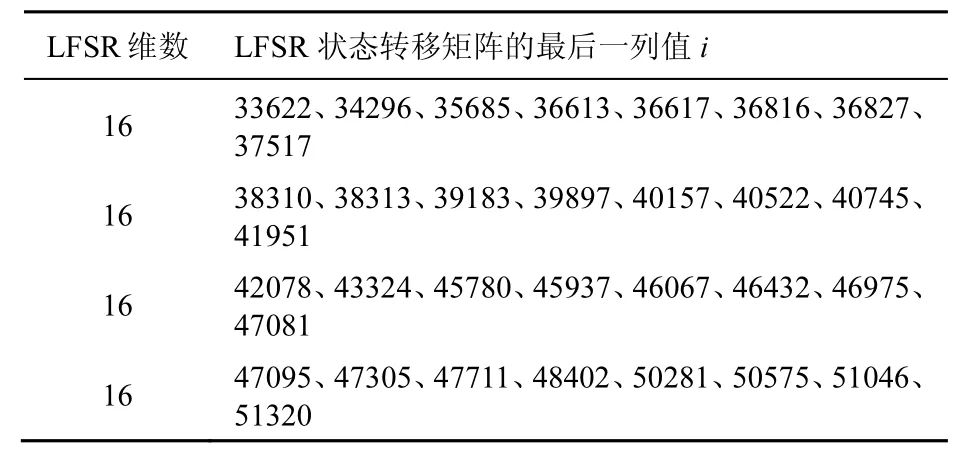
表10 利用16维LFSR构造出的分支数为7的二进制矩阵

表11给出了部分利用18维LFSR构造出的分支数为7的二进制矩阵，表中i表示18维LFSR状态转移矩阵的最后一列值。

表11 利用18维LFSR构造出的分支数为7的二进制矩阵

表12给出了部分利用32维LFSR构造出的分支数为11的二进制矩阵，表中i表示32维LFSR状态转移矩阵的最后一列值。

表12 利用32维LFSR构造出的分支数为11的二进制矩阵

5 结束语

扩散层作为分组密码的一个重要部件，在密码算法中扮演着重要角色，近几年，很多研究者都将目光转移到该问题上，产生了一系列的研究成果[27～56]。然而，目前的结果主要是面向硬件实现的，很少针对软件实现设计扩散层。本文首先介绍扩散层的研究现状，接着基于两大密码结构构造扩散层，分别是基于Feistel结构构造面向软件实现的扩散层和基于LFSR构造面向硬件实现的扩散层。

Feistel结构因其软硬件实现效率高，加解密一致，加解密速度快等优点受到广大研究者的青睐，Feistel结构不仅广泛应用于分组密码算法的整体设计中，而且也用来构造分组密码的主要部件S盒和扩散层。本文基于三轮Feistel结构构造轻量级扩散层，轮函数采用基于循环移位和异或的线性变换，构造出了一系列作用在和上分支数为 7的对合扩散层，一方面，对合性质使扩散层的加密和解密操作在硬件上可以使用相同的电路，在软件上可以使用相同的代码，并且轮函数采用基于循环移位和异或运算的线性变换，在支持循环移位指令的处理器中，循环移位运算通常可以通过一条指令实现，而在不支持循环移位的处理器中，通常只需要将该指令分解成3条指令：逻辑左移1次、逻辑右移1次、两者异或[67]。不管是移位运算还是循环移位运算，软件实现所需的CPU周期数均很低，大大提高了软件实现效率；另一方面，对于作用在8个4 bit或8 bit S盒上的扩散层，分支数为7的扩散层已经可以提供较好的扩散效果，并且分支数为7的扩散层是安全性和效率方面的权衡。

LFSR因其具有原理简单、计算速度快、便于硬件实现等优点，通常被用来构造密钥流生成器，而且也被用来构造分组密码的扩散层[7,13,14,29,30]，基于 LFSR构造的扩散层具有很高的硬件实现效率，扩散层只需实现LFSR且能在不需要额外逻辑控制电路的情形下重用已有的存储，大大降低了硬件消耗。本文基于LFSR构造出作用在和上的次最优扩散层，这些次最优扩散层应用于软硬件要求极其苛刻的环境下，可以使密码算法软硬件消耗极度降低。利用LFSR也构造出了作用在和上分支数为7的扩散层。另外，二进制矩阵相对于MDS矩阵（实现过程需要异或、查表和xtime操作[68]）而言，实现过程只需要异或操作，具有较高的软硬件实现效率，非常适合轻量级密码的设计，本文利用n维LFSR构造了作用在上n × n大小的二进制矩阵，列出了维二进制矩阵的分支数，并给出了采用LFSR构造的6、7、8维MDBL矩阵的具体构造，以及分支数分别为7、7、12的16、18、32维二进制矩阵的具体构造。本文构造的扩散层在轻量级密码的设计方面具有较高的应用价值。

[1] SCHNEIER B, SCHNEIER B. Data encryption standard (DES)[C]// Advances in Cryptology — EUROCRYPT’ 85. 1985:3-5.

[2] DAEMEN J, RIJMEN V. The design of Rijndael: AES, the advanced encryption standard[M]. Berlin: Springer,2002.

[3] 无线局域网产品中使用的 SMS4算法[EB/OL]. http://www. oscca.gov.cn/UpFile/200621016423197990.pdf. SMS4 algorithm used in wireless LAN products[EB/OL]. http://www. oscca.gov.cn/UpFile/200621016423197990.pdf.

[4] HONG D, SUNG J, HONG S, et al. HIGHT: a new block cipher suitable for low-resource device[C]//Cryptographic Hardware and Embedded Systems. 2006: 46-59.

[5] BOGDANOV A, KNUDSEN L R, LEANDER G, et al. PRESENT: an ultra-lightweight block cipher[C]//Cryptographic Hardware and Embedded Systems .2007:450-466.

[6] SHIRAI T, SHIBUTANI K, AKISHITA T, et al. The 128 bit blockcipher CLEFIA[C]//The 14th International Conference on Fast Software Encryption. 2007:181-195.

[7] GUO J, PEYRIN T, POSCHMANN A, et al. The LED block cipher[C]//Cryptographic Hardware and Embedded Systems. 2011: 326-341.

[8] WU W, ZHANG L. LBlock: a lightweight block cipher[C]//Applied Cryptography and Network Security. 2011: 327-344.

[9] BORGHOFF J, CANTEAUT A, GÜNEYSU T, et al. PRINCE—a low-latency block cipher for pervasive computing applications[C]// The International Conference on the Theory and Application of Cryptology and Information Security. 2012: 208-225.

[10] RAY B, DOUGLAS S, JASON S. The simon and speck families of lightweight block ciphers[R]. 2013.

[11] GÉRARD B, GROSSO V, NAYA-PLASENCIA M, et al. Block ciphers that are easier to mask: How far can we go?[C]// International Workshop on Cryptographic Hardware and Embedded Systems. 2013: 383-399.

[12] YANG G, ZHU B, SUDER V, et al. The simeck family of lightweight block ciphers[C]//The International Workshop on Cryptographic Hardware and Embedded Systems. 2015: 307-329.

[13] GUO J, PEYRIN T, POSCHMANN A. The photon family of lightweight Hash functions[C]//Advances in Cryptology Conference. 2011:222-239.

[14] ANDREEVA E, BILGIN B, BOGDANOV A, et al. Submission to the CAESAR competition[EB/OL].http://competitions.cr.yp.to/ round1/ primatesv1.pdf.

[15] RIJMEN V, DAEMEN J. The cipher shark[C]//Fast Software Encryption. 1996:99-112.

[16] SCHNEIER B, KELSEY J, WHITING D, et al. Twofish: a 128 bit block cipher[C]//The 1st AES Candidate Conference on National Institute for Standards and Technology. 1998.

[17] SCHNEIER B, KELSEY J, WHITING D, et al. The twofish encryption algorithm[M]. New York:John Wiley & Sons. 1999.

[18] DAEMEN J, KNUDSEN L R, RIJMEN V. The block cipher square[C]//The 4th Fast Software Encryption Workshop. 1997: 149-165.

[19] BARRETO P, RIJMEN V. The anubis block cipher[EB/OL]. http://www.larc.usp.br/～pbarreto/AnubisPage.html.

[20] BARRETO P, RIJMEN V. The khazad legacy-level block cipher[C]//Primitive Submitted to NESSIE. 2000.

[21] JUNOD P, VAUDENAY S. FOX: a new family of block ciphers[C]//Selected Areas in Cryptography. 2004:114-119.

[22] DAI W, FURUYA S, YOSHIDA H, et al. A new keystream generator MUGI[M]//Fast Software Encryption. Berlin: Springer, 2002:37-45.

[23] FILHO G D, BARRETO P, RIJMEN V. The maelstrom-0 Hash function[C]//The 6th Brazilian Symposium on Information and Computer Systems Security. 2006.

[24] GAURAVARAM P, KNUDSEN L R, MATUSIEWICZ K, et al. Grøstl a SHA-3 candidate[EB/OL]. http://www.groestl.info.

[25] BARRETO P S L M, RIJMEN V. The Whirlpool hashing function[EB/OL].http://read.pudn.com/downloads67/sourcecode/disk/2 40939/Whirlpool.pdf.

[26] MORADI A, POSCHMANN A, LING S, et al. Pushing the limits: a very compact and a threshold implementation of AES[C]//Advances in Cryptology – EUROCRYPT .2011.

[27] 崔霆, 金晨辉. 对合 Cauchy-Hadamard型 MDS矩阵的构造[J].电子与信息学报, 2010, 32(2):500-503.

CUI T, JIN C H. Construction of involution cauchy-hadamard type MDS matrices[J]. Journal of Electronics & Information Technology, 2010, 32(2): 500-503.

[28] SAJADIEH M, DAKHILALIAN M, MALA H, et al. On construction of involutory MDS matrices from Vandermonde Matrices in GF [J]. Designs, Codes and Cryptography, 2012, 64(3):287-308.

[29] SAJADIEH M, DAKHILALIAN M, MALA H, et al. Recursive diffusion layers for block ciphers and Hash functions[C]//The International Conference on Fast Software Encryption. 2012:385-401.

[30] WU S, WANG M, WU W. Recursive diffusion layers for (lightweight)block ciphers and Hash functions[C]//Selected Areas in Cryptography. 2012:355-371.

[31] AUGOT D, FINIASZ M. Exhaustive search for small dimension recursive MDS diffusion layers for block ciphers and Hash functions[C]//IEEE International Symposium on Information Theory Proceedings.2013:1551-1555.

[32] BERGER T P. Construction of recursive MDS diffusion layers from Gabidulin codes[C]//INDOCRYPT. 2013:274-285.

[33] AUGOT D, FINIASZ M. Direct construction of recursive MDS diffusion layers using shortened BCH codes[C]// Fast Software Encryption.2014:3-17.

[34] KHOO K, PEYRIN T, POSCHMANN A Y, et al. FOAM: searching for hardware-optimal SPN structures and components with a fair comparison[C]//Cryptographic Hardware and Embedded System. 2014:433-450.

[35] SIM S M, KHOO K, OGGIER F, et al. Lightweight MDS involution matrices[C]//Fast Software Encryption. 2015:471-493.

[36] NAKAHARA J, ABRAHO L. A new involutory MDS matrix for the AES[J]. International Journal of Network Security, 2009, 9(2): 109-116.

[37] GUPTA K C, RAY I G. On constructions of circulant MDS matrices for lightweight cryptography[C]// Information Security Practice and Experience. 2014:564-576.

[38] LIU M, SIM S M. Lightweight MDS generalized circulant matric-es[C]// Fast Software Encryption. 2016.

[39] LI Y, WANG M. On the construction of lightweight circulant involutory MDS matrices[C]// Fast Software Encryption. 2016.

[40] KWON D, KIM J, PARK S, et al. New block cipher: ARIA[C]// ICISC. 2003:432-445.

[41] AOKI K, ICHIKAWA T, KANDA M, et al. Camellia: a 128 bit block cipher suitable for multiple platforms design and analysis[C]//Selected Areas in Cryptography. 2000:39-56.

[42] KANDA M, MORIAI S, AOKI K, et al. E2—a new 128 bit block cipher[J]. Ieice Transactions on Fundamentals of Electronics Communications & Computer Sciences, 2000, 83(1):48-59.

[43] IZADI M, SADEGHIYAN B, SADEGHIAN S S, et al. MIBS: a new lightweight block cipher[C]//The International Conference on Cryptology and Network Security.2009:334-348.

[44] BANIK S, BOGDANOV A, ISOBE T, et al. Midori: a block cipher for low energy[C]//The International Conference on the Theory and Application of Cryptology and Information Security. 2014: 411-436.

[45] BILGIN B, BOGDANOV A, KNEŽEVIĆ M, et al. Fides: lightweight authenticated cipher with side-channel resistance for constrained hardware[C]//The International Workshop on Cryptographic Hardware and Embedded Systems. 2013: 142-158.

[46] SASAKI Y, TODO Y, AOKI K, et al. Minalpher v1[C]//Submission to the CAESAR Competition. 2014.

[47] KWON D, SUNG S H, SONG J H, et al. Design of block ciphers and coding theory[J]. Trends in Mathematics, 2005, 8(1): 13-20.

[48] KOO B W, JANG H S, SONG J H. Constructing and cryptanalysis of a 16×16 binary matrix as a diffusion layer[C]//The International Workshop on Information Security Applications. 2003:489-503.

[49] KOO B W, JANG H S, SONG J H. On constructing of a 32×32 binary matrix as a diffusion layer for a 256-bit block cipher[C]// Information Security and Cryptology (ICISC). 2006:51-64.

[50] KANG J S, HONG S, LEE S, et al. Practical and provable security against differential and linear cryptanalysis for substitution permutation networks[J]. ETRI Journal, 2001, 23(4): 158-167.

[51] KANDA M, TAKASHIMA Y, MATSUMOTO T, et al. A strategy for constructing fast round functions with practical security against differential and linear cryptanalysis[C]//Selected Areas in Cryptography. 1998: 264-279.

[52] GAO Y, GUO G. Unified approach to construct 8×8 binary matrices with branch number 5[C]// The 1st Acis International Symposium on Cryptography, and Network Security, Data Mining and Knowledge Discovery, E-Commerce and ITS Applications, and Embedded Systems. 2010:413-416.

[53] ASLAN B, SAKALLI M. Algebraic construction of cryptographically good binary linear transformations[J]. Security and Communication Networks, 2014, 7(1):53-63.

[54] SAKALL M T, ASLAN B. On the algebraic construction of cryptographically good 32×32 binary linear transformations[J]. Journal of Computational & Applied Mathematics, 2014, 259: 485-494.

[55] SAKALL S M T, ASLAN B. Algebraic construction of 16×16 binary matrices of branch number 7 with one fixed point[EB/OL]. http://www.singacom.uva.es/～edgar/cactc2012/trabajos/CACT2012_ Sakalli.pdf.

[56] DEHNAVI S M, RISHAKANI A M, SHAMSABAD M R M. Bitwise linear mappings with good cryptographic properties and efficient implementation[J]. Antiquity, 2015, 75.

[57] LIM C H. CRYPTON: a new 128-bit block cipher[J]. Nist Aes Proposal, 1998.

[58] ETSI/SAGE TS 35.222-2011, Specification of the 3GPP Confidentiality and Integrity Algorithms 128-EEA3 & 128-EIA3; Document 2: ZUC Specification[S].

[59] STERN J, VAUDENAY S. CS-Cipher[J]. Lecture Notes in Computer Science, 1998, 1372:189-205.

[60] MATSUI M. New block encryption algorithm MISTY[C]//The International Workshop on Fast Software Encryption. 1997:54-68.

[61] LI Y, WANG M. Constructing s-boxes for lightweight cryptography with feistel structure[C]//Cryptographic Hardware and Embedded Systems.2014:127-146.

[62] CANTEAUT A, DUVAL S, LEURENT G. Construction of lightweight s-boxes using feistel and misty structures[C]//The International Conference on Selected Areas in Cryptography. 2015: 373-393.

[63] GUO Z, WU W, GAO S. Constructing lightweight optimal diffusion primitives with feistel structure[C]//The International Conference on Selected Areas in Cryptography. 2015: 352-372.

[64] 张雪锋, 范九伦. 基于线性反馈移位寄存器和混沌系统的伪随机序列生成方法[J]. 物理学报, 2010, 59(4):2289-2297.

ZHANG X F, FAN J L. Pseudo-random sequence generating method based on LFSR and chaotic system[J]. Acta Physica Sinica, 2010, 59(4):2289-2297.

[65] STALLINGS W. Cryptography and network security: principles and practice, fifth edition[M]. Pearson Education, 2011.

[66] TODO Y, AOKI K. Wide trail design strategy for binary mixcolumns[M]. Applied Cryptography and Network Security. 2016.

[67] 公丽丽. 分组密码的软件实现评估方法研究及RECTANGLE在X86平台的软件实现测评[D]. 北京: 中国科学院大学, 2015.

GONG L L. A study of software implementation of block cipher and software implementation of RECTANGLE on X86 platforms[D]. Beijing: The University of Chinese Academy of Sciences, 2015.

[68] NAKAHARA J,ABRAHÃO E. A new involutory MDS matrix for the AES[J].International Journal of Network Security, 2009, 9(2): 109-116.

Construction of diffusion layers based on cipher structures

LI Peng-fei1,2

(1. The State Key Lab of Information Security, Institute of Information Engineering, Chinese Academy of Sciences, Beijing 100093, China; 2. School of Cyber Security, University of Chinese Academy of Sciences, Beijing 100049, China)

Taked diffusion layers of block cipher algorithms as the research object, lightweight diffusion layers were constructed by two cipher structures based on the characteristics of diffusion layers of lightweight block cipher algorithms, which were the construction of software-oriented diffusion layers based on Feistel structure and the construction of hardware-oriented diffusion layers based on LFSR. Lightweight involution diffusion layers with branch numbers 7 over eight 4-bit and 8-bit S-boxes were constructed by 3-round Feistel structure and the round functions adopt linear transformations with rotation and XORs. Some suboptimal diffusion layers over four 4 bit and 8 bit S-boxes and diffusion layers with branch numbers 7 over eight 4 bit and 8 bit S boxes based on LFSR were constructed. In addition, 6, 7, 8 dimension MDBL matrices and many 16, 18, 32 dimension binary matrices with big dimension and branch numbers 7, 7, 12 based on LFSR were constructed. The experimental results have high practical significance in realm of the design of block cipher algorithms.

block cipher, diffusion layer, Feistel structure, linear feedback shift register, MDBL matrix

The National Natural Science Foundation of China (No.61379142)

TP393

10.11959/j.issn.2096-109x.2017.00170