论一维δ势阱定态问题的求解方法

2017-07-05唐世清许成科苏卫平汪新文

湖南科技学院学报 2017年6期

唐世清　许成科　苏卫平　汪新文

论一维δ势阱定态问题的求解方法

唐世清1许成科2苏卫平3汪新文1

（1.衡阳师范学院物理与电子工程学院，湖南衡阳 421002；2.衡阳师范学院南岳学院，湖南衡阳 421008；3.湖南省益阳市南县第一中学，湖南益阳 413200）

一维势阱的束缚态问题是量子力学中重要的一维定态问题。由于存在奇异点，数学上的处理与其它的一维定态问题有很大不同。本文归纳、总结和分析对比一维δ势阱束缚态求解的三种解法（积分极限法、傅里叶变换法和动量表象法），通过详细的推导过程，展现各种方法的优缺点。对各种方法的特点的分析不仅有利教师和学生对相关问题的理解，更有利于激发了学生的学习兴趣、培养了学生的创新思维。在笔者多年的教学实践中，收到了较好的教学效果。

量子力学；势阱；傅里叶变换；动量表象

1　引　言

在物理学、数学和现代工程技术等许多领域中，人们都是通过建立物理模型来分析问题。对于物理量集中于空间某一点或时间的某一瞬间是经常遇到的两种物理情况。人们为了更好地抽象出物理图像，抓住主要矛盾，就建立了理想化的模型。如集中质量和集中电荷，就分别对应质点和点电荷；此外，还有瞬间冲量，瞬时作用力等。从数学上讲，这里面蕴含着某些空间点或时间点会出现无穷大的分布，为了解决这类包含某种无穷大的量以及不连续函数的微分等问题, 著名物理学家狄拉克(Dirac)引入了函数。后来，物理学家们更是广泛地使用函数描述物理学中的一切点量和瞬时量，不仅方便而且物理意义非常清楚。严格说来，函数不是传统数学中的函数，它只是一种分布。但是函数具有一些特殊性质，例如局部无限突变、整体积分有限性等，为我们解决一些抽象的物理问题提供了一种量化模型，从而使复杂的问题变得简单。也正是由于这一点，使得函数在近代物理和工程技术领域都有着比较广泛的应用[1-4]。

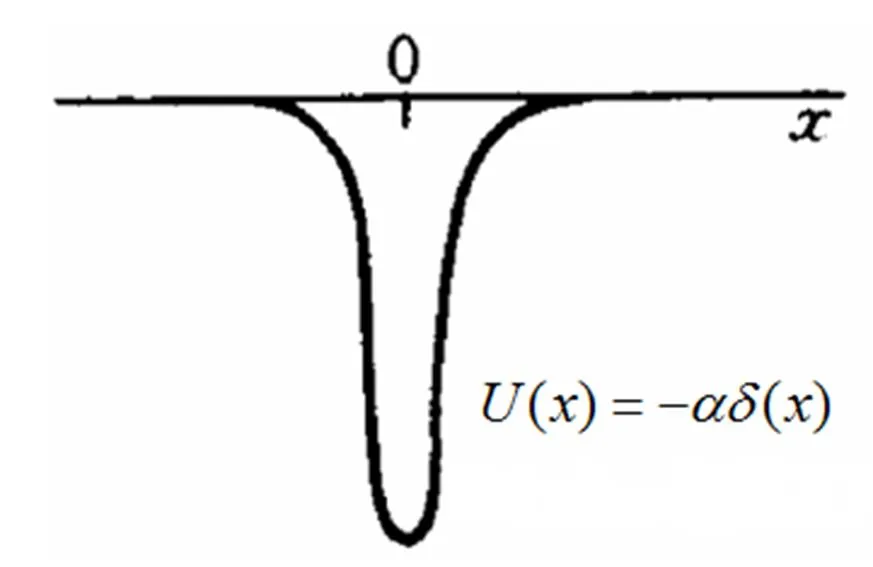
图1.势阱示意图

2　积分极限法求解势阱中的束缚态的优缺点分析

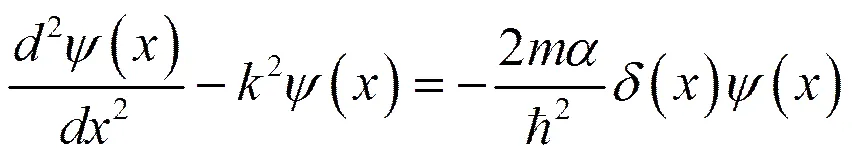
(2)

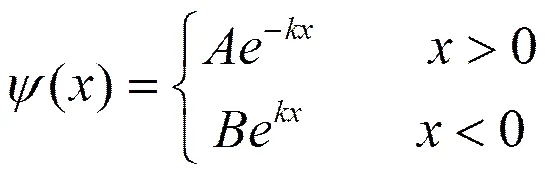
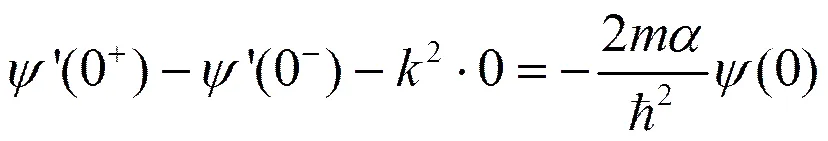
由此可得出粒子能量的本征值

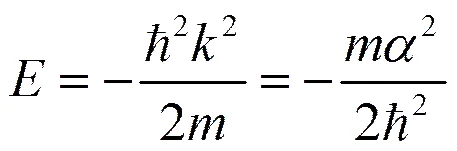
(7)

这种方法数学求解过程看似简单，学生理解起来有些困难。这是因为势场是函数，具有奇异性，在时，于是，从而导致了导数在不连续。所以需要分和来讨论。甚至还有部分学生根据无限深势阱求解的经验想当然的认为：由时,得出这样错误的结论。究其原因还是因为对不理解所致。的函数图像是无限高而无穷窄的，只有在积分下才有意义的。

3　傅里叶变换法求解势阱中的束缚态的优缺点分析

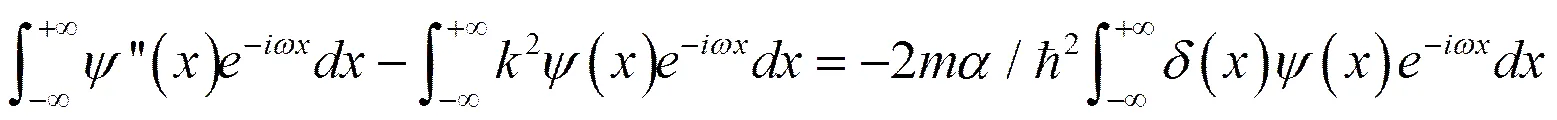
(9)

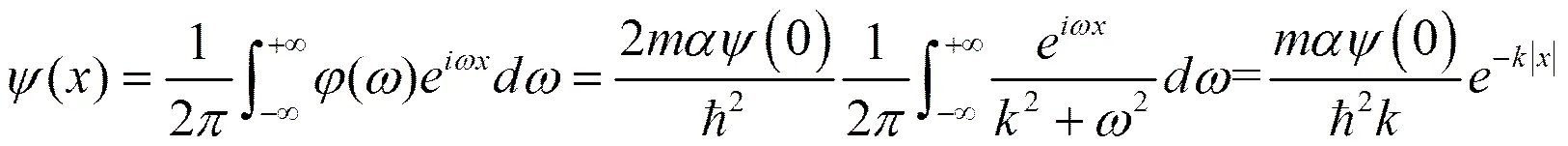
这种方法数学求解过程看起来好像复杂一些，需要用到傅里叶变换的导数定理，甚至学生还要求解一个很复杂的积分。其实这个导数定理和复杂积分都是《数学物理方法》教材上有的，完全没有必要担心。但这种方法的整个求解更为流畅自然，物理思想明确，思路清晰，无需分区讨论，也不必绕开奇异点，甚至不用考查波函数一阶导数的不连续性，也不会犯低级错误。

4　动量表象下求解势阱中的束缚态的优缺点分析

除了上述两种方法外，我们还可以转到动量表象下求解。动量表象中的能量本征方程由下式给出

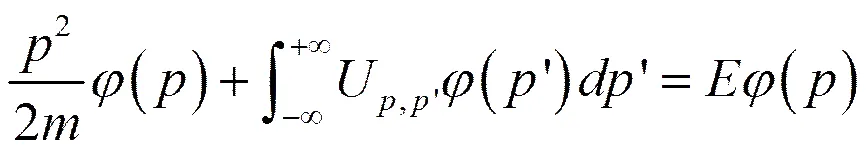
(12)

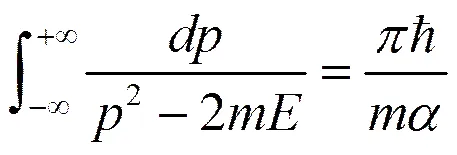
(14)

这种方法同样也无需分区讨论，不用考查波函数一阶导数的不连续性。其本质仍是傅里叶变换，但却不需要导数定理，这是因为动量表象下的能量本征方程是以动量为自变量的。同时，这种方法有利于学生理解在动量空间下求解量子力学问题的方法，因为对于大部分学生而言熟悉的都是坐标表象。事实上，有些问题如果转到动量空间去计算，可能会收到意想不到的简捷奇妙之效。