翻转课堂模式下《数学分析》课程教学方式

赵艳辉　唐作明



翻转课堂模式下《数学分析》课程教学方式

赵艳辉1唐作明2

（1.湖南科技学院 理学院，湖南 永州 425199；2.湖南省永州市教育科学研究院，湖南 永州 425000）

利用“翻转课堂”教学模式，从教学视频的制作、教学内容的设计、翻转课堂的开展等方面对《数学分析》课程教学模式进行了探讨。旨在转变教师的教学方式，培养学生的自主学习能力、研究能力和创造性思维能力，为学生的可持续发展打下基础。

翻转课堂；《数学分析》课程；教学方式

翻转课堂译自“Flipped Classroom”或“Inverted Class-room”，是指教师将课程重点、难点和部分新知识进行重构创建相关教学视频，学生利用课下时间预先通过观看教学视频自主学习新的课程，自主完成在线测试，完成对新知识的吸收内化，最后带着学习过程中的疑问参与课堂上师生、生生之间的互动交流、合作与讨论，实现其对新知识的完全理解和熟练掌握，从而完成学习的过程[1]。因此“翻转课堂”创设了学生自主学习的环境，有助于学生寻找适合自己的课外学习方式，改变了单纯依赖老师传授的传统教学模式。翻转课堂的内容可被永久的保存,可供查阅和修改, 所有的学生都能获得个性化教育。

《数学分析》是大学数学专业最重要的一门专业基础课，是本科乃至研究生阶段很多后继课程的深化或应用。对数学分析课程的教学改革不少重点本科院校从数学分析的内容、教材结构体系、教育教学方法、作业批改等很多方面做了有益的尝试，取得了很好的成绩。但这些改革仍然是以教师的讲为中心的，在课堂上大多是老师讲、学生听，老师是主体。学生自由思考的空间不多，学习的主动性未能充分调动起来，主体地位没有得到充分体现。本文将在“翻转课堂”的基础上从教学视频的制作和翻转课堂的开展等方面探讨教师的教学方式，旨在培养学生的自主学习能力、研究能力和创造性思维能力，为学生的可持续发展打下基础。

1　精心制作教学视频

翻转课堂的教学过程包括课前的自主学习(知识传授)和课堂的互动学习(知识内化)两个阶段。课前,学生根据自己的学习情况选择合适的学习时间和学习空间,掌握学习内容和学习进度,课堂上,学生积极参与教师、同学的交流互动，进一步深化和理解新知识。因此学生课前自主学习授课视频效果的好坏将直接影响到翻转课堂上知识内化过程的实施与好坏，是推行“翻转课堂”的先决条件。

1.1创设适当的教学情境，以问题链方式呈现教学视频

人类学习是一种自发的、有目的的、有选择的学习过程。在《数学分析》课程中，以现实背景导入数学知识，或创设一些有意义的问题，引发学生思考。如为什么要引入极限概念？介绍极限概念产生过程中的无穷小悖论，也可以增加一些趣味数学知识，穿插一些数学美、数学史和数学家们的奇闻逸事等人文主义教学内容，提高学生观看视频课的兴趣。同时在教学中教师要相信学生的潜能，注意科学引导。有教育工作者指出：“有趣的思考胜过千言万语的赞美。学习成绩高的学生，并不是预期会得到好的奖赏，而是将学习当成一趟有趣的发现之旅，不断地发现学习的乐趣。”

1.2深入浅出，以数学思想方法贯穿教学视频

知识是人类智慧的结晶，是数学家们思想的体现和人格力量的外化，知识是能力的基础。在教学中，一位优秀的教师不仅会考虑怎样将知识传授给学生，还会考虑怎样激发学生的学习兴趣，培养学生自主学习的习惯、意识和能力。所以在教学中教师要根据自己的人生阅历、生活经验和知识背景，结合学生的实际生活、学习情况，深入浅出地引导学生去发掘和领会知识产生过程中数学家们的思维劳动，总结数学思想方法。如导数和积分是数学分析课程中的两个重要概念，在教学中，我们要鼓励学生依据所学过的相关数学知识对将要学习的新数学概念下定义，而不是教师直接写出概念。事实上，导数处理的是非均匀量的商，定积分处理的是非均匀量的积。求均匀量的商与积我们可以用除法和乘法，但现实生活和科学技术工作中大量存在的是非均匀量的处理问题，这样就有了导数和积分的定义。揭示问题的本质不仅显示了导数和积分的重要性，同时也指出了导数和积分的应用方向。

在知识的传授过程中要教渗透在知识当中的科学家们的智慧、丰富的数学思想方法和前辈数学家们的人格魅力。例如在学习定积分概念时，不仅仅是掌握定积分概念这个知识点，更重要的是教会学生思考数学家们是怎样提出定积分概念的，其中蕴含的数学思想方法是什么？除了教教材中现成的知识外，我们还要在课堂中教学生怎样做数学研究，教学生研究问题的方法，使学生感受到老一辈数学家们的人格魅力，使自己的人格得到升华。从而培养学生的合情推理与演绎推理能力，体会数学分析中的转化与化归思想，学会用数学的眼光来分析问题、解决问题。

2　有效开展翻转课堂

翻转课堂与传统的课前预习不同之处在于：传统的课前预习是学生在无人指导的情况下的自学，课堂上老师会继续讲解新知识，这样学生通常会在开学前预习一段时间，到后面就觉得没必要了，反正课堂上老师都要讲的。而翻转课堂是学生按照老师给的学习任务有针对性的自主学习，并实时检测自己的学习情况，课堂上老师不再继续讲解新知识，而是和学生一起讨论学生课前提出的问题并进行解答，能及时发现学生的知识漏洞。

如在讨论二元函数可微性与偏导数的定义时，可以提出以下两个问题引入课题：

问题1：在一元函数中, 函数在一点连续、可导和可微三者的关系是什么？

问题2：在二元函数中这些结论还成立吗?

由此引导学生思考多元函数在一点的全微分和偏导数的定义，并学会将未知的知识和已知的知识建立联系。接着由一元函数连续、可导与可微的关系引导学生结合二元函数的全微分和偏导数定义思考以下问题：

问题3：如果二元函数在一点可偏导，那么该二元函数在这点可微吗？即一元函数中可导和可微等价在这里还成立吗？请学生思考并猜想，同时考虑以下例1。

引导学生从函数的连续性、可微性定义出发通过自主探究、小组合作等方式解决问题，加深对相应数学概念的理解。最后展示解答过程。

例1表明，即使函数在一点连续且存在偏导数，函数在这一点也不一定可微，由此得到函数在一点可微的必要条件。

问题4：二元函数在一点连续且偏导数存在时, 还需要什么条件函数才在该点可微?

引导学生主动探索，再一次从二元函数可微的数学定义出发，体会数学定义在数学学习中的重要性。从而得出二元函数在一点可微的充分条件。

问题5：二元函数在一点可微时函数在该点的偏导数连续吗？考察例2：

引导学生根据前面问题的分析进行自主探索研究、小组合作等方式解决问题。最后展示解答过程。

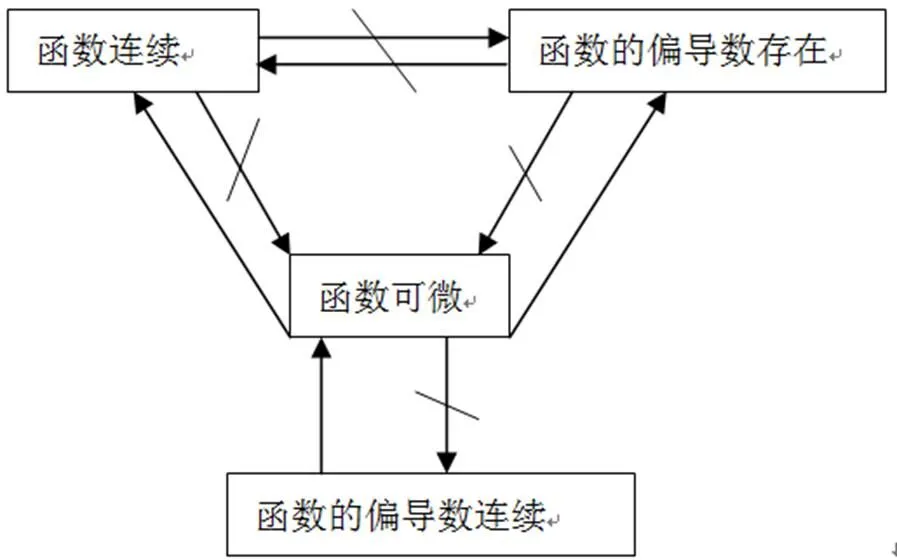
课堂上，教师组织引导学生进行讨论和交流，从而可以发现学生在解题中出现的“懂而不会”现象的原因。如对教学设计中的例1、2的问题大多数学生都是“懂而不会”，这时老师要引导学生从函数的连续性、偏导数的存在性、可微性及偏导数的连续性定义出发通过自主探究、小组合作等方式解决问题，加深对相应数学概念的理解，并通过类似例题加强对数学概念的理解和掌握。最后多媒体展示解答过程。

通过翻转课堂，学生在自身能力范围内已对所学内容进行了充分的思考和理解，学生在知识建构过程中产生的疑惑可在翻转课堂上向老师、同学请教，同时老师可构建一些有探究价值的问题，供学生选择探究，使学生和老师在探究问题的过程中产生思维的共鸣，提高学生的参与率，真正实现课堂教学效果的最大化。

[1]张金磊,王颖,张宝辉.翻转课堂教学模式研究[J].远程教育杂志,2012,(8):46-51.

[2]孙炯,杨联贵,等.数学视频公开课建设的实践与思考[J].中国大学教育,2003,(4):12-14.

[3]钟秉林,方芳.“慕课”发展与大学人才培养模式改革[J].中国高等教育,2015,(11):24-28.

[4]郝兴伟,张强.翻转课堂教学:经验与趋势[J].中国大学教育,2015,(10):65-67.

（责任编校：何俊华）

2017－01－20

湖南省教育科学“十二五”规划项目“翻转课堂教学模式下学生学习方式的探索与研究”（项目编号XJK015CGD023）研究成果。

赵艳辉（1969－），女，湖南益阳人，副教授，研究方向为数学与教学。

G424.1

A

1673-2219（2017）06-0010-02