某型号加工中心整机模态的分析测试及预测评价*

闫文飞，米 洁，王福乾

(北京信息科技大学 机电工程学院，北京 100192)



某型号加工中心整机模态的分析测试及预测评价*

闫文飞，米 洁，王福乾

(北京信息科技大学 机电工程学院，北京 100192)

为了准确、有效、快速地获取某型号加工中心整机的固有频率和振型，结合改进弹簧刚度法与虚拟材料法对某加工中心关键结合面进行了处理，建立了该加工中心的有限元模型。采用有限元分析法获得了该加工中心的前4阶模态参数，以有限元分析结果为指导，确定模态测试的布点密度、测点位置、采样频率、边界条件等试验参数;采用SIMO锤击法对该加工中心进行模态测试，通过比照模态分析与模态测试的结果，修正仿真模型获得更为精确的仿真模型。分析结果表明：使用改进的弹簧刚度法与虚拟材料法比单独使用弹簧刚度法及虚拟材料法能够更加准确地拟合试验结果。最后，根据机床实际工况确定边界条件，以模态仿真结果为依据对机床动态特性进行评价，为后续建立机床适应性评价体系提供了可行、准确的特征参数提取方法。

加工中心；模态分析；模态测试；动态特性评价

0 引言

机床由许多零部件组成，零部件之间的连接方式多种多样。如螺栓紧固连接、平面导轨和滚动导轨的滑动连接以及转子支撑连接等等[1]，这些连接便构成了结合面。据统计，机床静刚度的(30～50)%源自结合面的刚度特性，且总阻尼值的 90%以上来源于结合面[2]。因此，如何快速获取结合面参数是模态分析过程的重中之重。在机床领域，常采用有限元及试验模态分析相结合的方法，即采用试验模态参数修正有限元模型，以获得精确、有效的虚拟样机[3-6]。另外建立较为合理的有限元模型，也有助于设计师在设计或试制阶段对机床动态特性进行有效评估[7]。所以，模态分析的重点是如何建立准确、有效、合理的有限元模型。

首先，本文采取一种改进的弹簧刚度法与虚拟材料法相结合的方法对某加工中心关键结合面进行了处理，建立了该加工中心的有限元模型。然后，分别采用改进的弹簧刚度-虚拟材料法、弹簧刚度法、虚拟材料法对机床进行了模态分析；并采用SIMO锤击法进行了模态测试。比照模态分析与模态测试的结果，表明使用改进的弹簧刚度法与虚拟材料法比单独使用弹簧刚度法及虚拟材料法能够更加准确地拟合试验结果。最后，根据机床实际工况确定边界条件，以模态仿真结果为依据对机床动态特性进行评价。

1 结合面处理方法及其参数识别方法

1.1 结合面处理方法

目前主流的虚拟模型结合面处理方法有：节点耦合法、弹簧法、弹簧-阻尼法、虚拟材料法等。综合各方法的优缺点，本文采用了一种改进的弹簧法和虚拟材料相结合的方法来进行模态分析。该方法综合了弹簧刚度法与虚拟材料法的优点，有效避免了他们的不足。

该机床主要结合面包括螺栓结合面和导轨结合面，本文采用虚拟材料法处理机床与地面间的接触面，有效减弱了外部因素带来的影响。其余结合面采用改进弹簧法，有效地减少了计算量，缩短了分析时间。

1.2 结合面参数识别方法

目前国内众学者对结合面参数识别方法的研究主要集中在两个方面：①通过大量试验获得结合面参数，并基于特征参数建立结合面特性的数学模型[8-10]；②基于赫兹接触理论及统计理论推导结合面接触数学模型，如，以分形几何为基础的MB模型[11-13]。然而，上诉的方法过于繁琐不适合工程的应用。文献 [14-15]中运用已建立的结合面特性经验公式对机床结合面刚度进行了计算和拟合，但其并未考虑结合面三向刚度之间的耦合关系。因此，本文对结合面刚度计算过程加以改进，认为每个方向的刚度都与其他方向的刚度有关。

设每个接触面都有三个方向的刚度分别为kx、ky、kz，法向刚度knx、kny、knz，切向刚度kτx、kτy、kτz则有：

(1)

各方向法向刚度和切向刚度计算公式为：

kni(kτi)=αpβΔS

(2)

式中：kni(kτi)—法向(切向)刚度(i=x、y、z),单位N/μm；p—法向面压，单位：MPa；α、β—与结合面的材料、加工方式、表面粗糙度和润滑等有关的参数；ΔS—实际接触面积，单位为m2。

该加工中心整体与地面接触的结合面采用虚拟材料法。运用文献[16]中虚拟材料法建立结合面数学模型并计算得到虚拟材料的参数，杨氏模量8.96×108N/m2、泊松比0.410、密度8.90×102kg/m3，该材料近似于聚乙烯(PPC)。

2 有限元模态分析及结果

2.1 有限元摸态分析

采用有限元软件ANSYS Workbench对图1所示的加工中心整机进行模态分析。模型简化处理后导入到ANSYS Workbench中，设置各部件材料属性如下：立柱、床身、垫块设置为HT300(杨氏模量1.30×1011N/m2、密度7300kg/m3、泊松比0.25)；其余为45#钢(杨氏模量12.09×1011N/m2、密度7.89×103kg/m3、泊松比0.269)；虚拟材料层近似为聚乙烯(PPC)(杨氏模量8.96×108N/m2、泊松0.410、密度8.90×102kg/m3)。依据部件大小采用合适的网格划分方法对各部件进行网格划分。对除机床与地面接触结合面外其他结合面采用改进弹簧法进行处理，将其结合面特征等效为三个方向的弹簧，每个弹簧对应一个刚度，弹簧刚度确定首先要对各结合面进行受力分析(此处涉及空间力系分配和求解)，得出结合面上各向所受的力。

图1 加工中心整机三维图

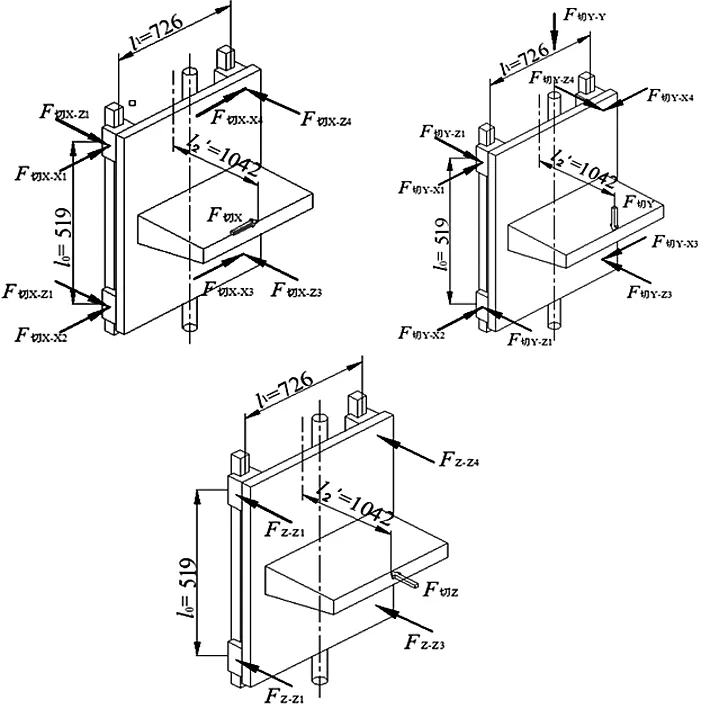
图2 Y向导轨在X、Y、Z三向的受力分析

以Y向导轨受力分析计算为例：如图2为Y向导轨在X、Y、Z三向的受力分析，将导轨所受力分配到各结合面上，以确定结合面相关参数：导轨与滑块间结合面接触属性：钢-铸铁接触，油润滑，表面粗糙度Ra=1.6，结合面法向参数α=1110430，β=0.63；切向参数α=156969，β=0.39。再计算得出结合面面压，最后通过式(1)和式(2)算出等效弹簧各向刚度。其他结合面计算与此类似，此处不做详述，结合面总计123个等效弹簧，只给出等效弹簧刚度值数值，如表1所示。

表1 各结合部等效弹簧刚度值 单位：N/μm

输入等效弹簧对应的刚度值，设置好虚拟材料属性，添加整机边界条件。整机床身下端垫有10个金属垫块，且未采用螺栓紧固，垫块下面设置厚度大约5mm的虚拟材料，此时垫块与整机、整机与地面之间有微小移动，但在整机重力作用下与地面的横向摩擦力约束了该位移。故对整机与垫块接触部分、整机底部添加fixed约束。其他不重要的结合面采用Bonded。至此有限元模型建立完毕，提交至求解器进行求解。

2.2 有限元摸态分析结果

整机有限元模态分析频率及振型如表2和图3所示。

表2 有限元模态分析结果 单位：Hz

图3 整机有限元模态分析前4阶振型

3 模态测试及结果分析

3.1 模态测试试验

采用东方振动噪声研究所模态试验测试分析设备，用SIMO锤击法进行模态试验。

整机安装复杂，工厂不便提供理想的试验环境，因此采用垫块将整机垫起。根据机床结构的特点和试验目的，以不遗漏模态为前提尽可能简化结构和零部件进行布点建模。

测点布置如图4所示，总测点数共789个。建模时为了简单分为10个小部件分别建模，完成后将各部件通过线面关系进行组装。建模时要避免布点重复，否则测量数据会产生叠加影响测量的精度。建模要选择合理的布点密度，疏密度要保持在可操作的范围之内。

激振点要保证系统的可辨识性，要避开机床各阶模态的节点和节线，以此尽可能多的激励结构模态。最好在试验之前进行预试验，通过不同方向、不同位置的响应来选择最优激振点，最后选择激振点位于图4高亮点处。设定好分析频率、采样频率等参数，采用变时基采样技术，以同时保证力信号的时间分辨率和响应信号的频率分辨率，变时基倍数为8。进行预试验调整各参数至最优状态，可进行试验，共击振获得263组数据，每组激振为三次，单次激振对应测点数为3。

图4 测点及激振点布置

3.2 模态测试试验结果与分析

采用Coinv DASP V10中集总平均法进行模态定阶识别，分析时忽略工频(50Hz)干扰产生的虚假模态。

试验结果如图5和表3所示，通过三种方法有限元模态分析结果与试验模态结果对比情况可知，本文所采用的方法明显比其他两个方法更加准确地拟合了试验的结果。虽然第1阶误差较大，但考虑到测量过程中工厂噪音过大，整机结构过大等因素,分析频率与试验频率误差在可以接受的范围之内，阻尼比小于5.5%，说明采用改进弹簧法与虚拟材料法相结合对关键结合面进行处理，建立的有限元模态分析仿真模型是较为准确的，能够通过该虚拟模型进行机床整机模态参数的预测。

图5 整机试验模态振型

表3 三种方法与试验模态结果对比情况 单位：Hz

根据分析与试验的结果可推断出整机的立柱与Z向导轨的结合面为其薄弱处，薄弱原因可能为立柱筋板刚度不足，结合面刚度不够。故提出如下建议：机床整机的重心偏高，应适当的降低整机重心。

4 整机加工状态模态参数预测

该机床在加工时，整机与地面是通过16个M30的地脚螺栓进行固定的，这与试验工况是不同的。因此采用改进弹簧法与虚拟材料法相结合对关键结合面处理，建立的有限元模态分析仿真模型对该加工中心在加工状态下的固有频率和振型进行预测。这样就可以在不进行模态试验的情况下对模态参数有一个初步的预测，可以大大减少机床整机模态参数获取的时间，避免了实验过程中大量劳动，使得模态参数获取更加快速，简便。预测显示振型与试验并未发生过大的改变，只是固有频率有所不同：1阶为38.558Hz，2阶为55.559Hz，3阶为81.972Hz，4阶为103.96Hz。

通过对20台加工中心的固有评论进行统计分析，可以得出前两阶固有频率的分布图如图6所示。

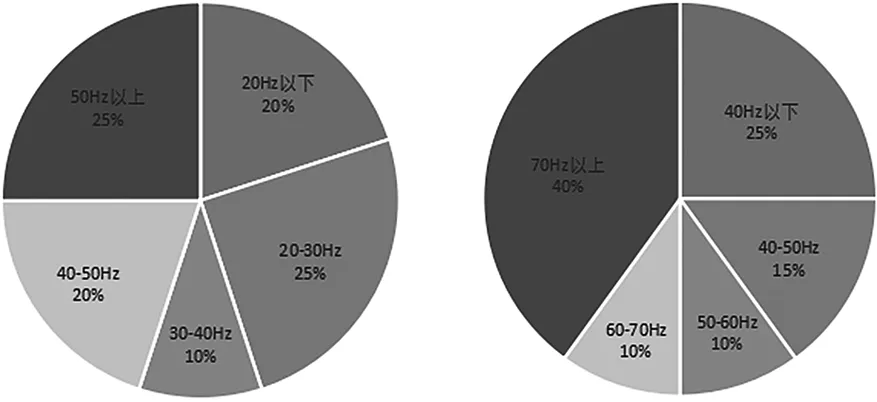
图6 前2阶固有频率的分布图

从图可知，80%的加工中心第一阶固有频率在20Hz以上，只有20%的在20Hz以下；75%的加工中心第2阶固有频率在40Hz以上，只有25%的在40Hz以下。该加工中心的前两阶固有频率分别在30～40Hz和50～60Hz的区间内。就固有频率而言，该加工中心属于同类产品中较为高档的。

5 结论

(1)相比单独使用弹簧法或虚拟材料法，结合两者对结合面处理的方法更加准确，为预测其他机床或结构提供了一种行之有效的方法。

(2)加工中心整机模态的分析测试结果表明：立柱与Z向导轨的结合面为其薄弱环节，应通过增加联接螺栓的数量或增加联接螺栓的预紧力来增大结合面刚度。

(3)该方法可以为机床刚度评价系统中机床模态参数的特征提取提供一定的借鉴，并对机床进行适应性评价提供了有效、准确的评价模型。

[1] 谭锋.高速卧式加工中心静动态性能分析与结构优化[D].成都:电子科技大学,2015.

[2] 程天昱.重型数控机床螺栓结合部动力学建模及影响因素研究[D]. 哈尔滨:哈尔滨理工大学,2015.

[3] 蒲凡,胡光忠,唐勇明,等.立式加工中心主轴箱结构分析与优化[J].组合机床与自动化加工技术,2016(8):12-15.

[4] 齐陆燕,王禹林,周斌,等.精密内螺纹磨削中心用磨杆静动态有限元分析及试验研究[J].组合机床与自动化加工技术,2013(9):9-12.

[5] 史科科,谢志坤,路平,等.基于ANSYS 的HTM40100动静态特性分析[J].组合机床与自动化加工技术,2013 (7):44-45,53.

[6] 谭峰,殷国富,方辉,等.基于ANSYS Workbench的微型数控车床主轴动静态性能分析[J].组合机床与自动化加工技术,2015(4):29-32,36.

[7] 穆希望,米洁. 基于关键螺栓结合面的立主轴模态分析[J].制造技术与机床,2014(8):78-82.

[8] 蔡力钢,王锋,李玲,等.栓接结合部动态特性研究进展[J].机械工程学报,2013,49(9):158-168.

[9] 武友德,李柏林.TJK6916机床结合面参数优化识别[J].机械设计与研究,2013,29(4):103-106.

[10] 杨勇,张为民,陈希光,等.数控机床导轨滑块结合部组建模与参数辨识方法研究[J].农业机械学报,2014,45(7):313-320.

[11] 李小彭,梁亚敏,郭浩,等.结合面广义间隙的等效模型研究[J].振动工程学报,2014,27(1):25-32.

[12] 田红亮,钟先友,秦红玲,等.依据各向异性分形几何理论的固定结合部法向接触力学模型[J].机械工程学报,2013,49(21):108-122.

[13] 王南山,张学良,兰国生,等.临界接触参数连续的粗糙表面法向接触刚度弹塑性分形模型[J].振动与冲击,2014(9):72-77.

[14] 陈金.基于结合面的CKX53280铣车床整机动态特性分析[D].武汉:华中科技大学,2013.

[15] 米洁.高精度立式磨床关键结合面动态特性研究[J].机械科学与技术,2014,33(2):224-228.

[16]TIAN Hong-liang, LIU Hong-qi, LI Bing. A new method of virtual material hypothesis-based dynamic modeling on fixed joint interface in machine tools[J].International Journal of Machine Tools & Manufacture, 2011, 51(3):239-249.

(编辑 李秀敏)

The Modal Analysis, Test, Prediction and Evaluation of a Certain Type of NCPC

YAN Wen-fei, MI Jie, WANG Fu-qian

(Mechanical Electrical Engineering School,Beijing Information Science & Technology University, Beijing 100192,China)

In order to obtain the natural frequencies and vibration modes of a certain type of machining center. Combining the improved spring stiffness method and the virtual material method, the model of key binding surfaces of the machining center is processed and the finite element model of the machining center is established. The first four order modal parameters are respectively obtained by the finite element analysis. Based on the analysis results, the parameters of the modal test are determined, such as distribution density, measuring points, sampling frequency and boundary conditions etc. The modal test is carried out by using the SIMO hammering method and the more accurate simulation model is modified by comparing the results of modal analysis and modal test. The results shows the method can more accurately fit the test results than the spring stiffness method and the virtual material method. Finally, the boundary conditions are determined according to the actual working conditions of the machine tool, the dynamic characteristics of the machine tool are evaluated basing on the modal simulation results. It provides a feasible and accurate method to extract the characteristic parameters of the machine tool adaptability evaluation system.

machining center; modal analysis; modal test;modal prediction

1001-2265(2017)06-0093-04

10.13462/j.cnki.mmtamt.2017.06.024

2016-09-07；

2016-10-14

国家科技部04重大专项：“中小型航空发动机零件铣车加工单元研制”(2013ZX0400-1061)

闫文飞(1990—)，男，甘肃天水人，北京信息科技大学硕士研究生，研究方向为机械设计及数字化设计，(E-mail) yanwenfei1028@163.com。

TH122;TG506

A