精密定位平台柔性支撑杆屈曲分析*
2017-07-05伍建军欧阳丹廖泰健
伍建军,汪 辉,欧阳丹,李 南,廖泰健
(江西理工大学 机电工程学院,江西 赣州 341000)
精密定位平台柔性支撑杆屈曲分析*
伍建军,汪 辉,欧阳丹,李 南,廖泰健
(江西理工大学 机电工程学院,江西 赣州 341000)
针对工程机械关键结构精密定位平台柔性支撑杆在结构设计上普遍存在屈曲失稳问题。首先基于瑞利-里兹能量变分法,建立计算精密定位平台柔性支撑杆屈曲临界载荷的数学模型并与有限元的Block Lanczos方法所求其前1阶屈曲载荷和屈曲模态进行对比,结果表明理论值与实验值偏差不大于0.26%,验证了基于瑞利-里兹能量变分法建模的准确性。最后对柔性支撑杆进行参数研究,发现长度比L/l与屈曲临界载荷呈反比例,直径比D/d小于1.5对屈曲临界载荷影响较大,倒角半径R与屈曲临界载荷正相关,为密定位平台柔性支撑杆的设计提供新的思路。
柔性支撑杆;屈曲临界载荷;有限元分析;稳定性
0 引言
柔性支撑杆是机械工程中一种重要的支撑和传动设备,常用于机器人、精密仪器等领域。这种柔性支撑杆,具有较强的支撑精度和导向精度。其中间环节最易失稳,常因外载荷作用下,应力集中造成局部屈曲失稳,准确预测和优化结构临界载荷和失稳形式,具有重要的工程意义。对于杆的屈曲问题,以往文献已有很多研究[1-5]。文献[6]应用计算机仿真技术,建立新型圆柱杆柔性纤维数学模型,但是建模的模型是简化的屈曲形态不够准确。文献[7]Paidoussia推导了受两端约束的圆柱体在横向运动下的线性微分方程,研究了稳态和动态形式,但是没有对复杂载荷研究。Paidoussis等[8-9]给出了悬臂圆柱体的非线性数学模型,同时用数值模拟了其动态行为。文献[10]基于欧拉屈曲载荷,提出了柔性管屈曲解析解公式,但是得出的屈曲载荷值误差过大。关于对精密定位平台柔性支撑杆的屈曲问题深入研究很少,以往的建模方法存在不合理性,得出的精度不高,而且对结构设计的优化没有具体的研究。针对以往研究的不足,本文采用瑞利-里兹能量法建立精确屈曲数学模型,在ANSYS中运用APDL语言建立柔性支撑杆的有限元模型,研究精密定位平台柔性支撑杆在不同工艺要求下的屈曲现象;同时分析了长度比、直径比、倒角半径与柔性杆临界屈曲载荷的关系。对精密定位平台柔性支撑杆的深入复杂研究和同类杆件的研究具有一定的参考价值。
1 构建屈曲临界应力理论计算模型
图1所示为精密定位平台柔性支撑杆的结构示意图(以下简称:柔性支撑杆)。从势能驻值原理出发,推导瑞利-里兹能量法[11-13]求解临界载荷。
设柔性支撑杆下端固定,上端自由,在力P作用下处于临界屈曲状态。根据弯曲变形理论建立其数学理论模型(图2),在图2中L代表柔性支撑杆刚体长度,l代表支撑杆柔性长度。
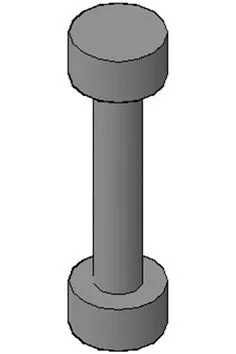
图1 柔性支撑杆
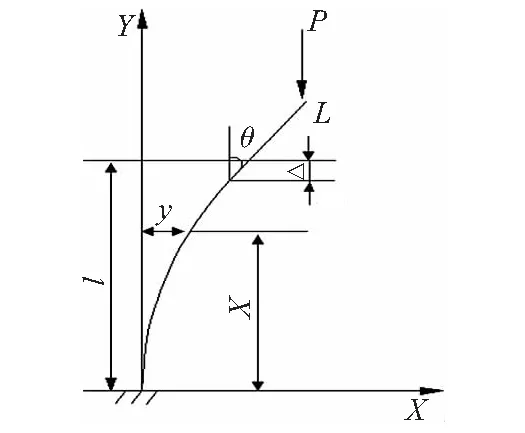
图2 柔性支撑杆屈曲数学模型
以柔性支撑杆的直线平衡位置为参考状态,对任一几何位移,其总势能为:
EP=U+UP=U-PΔ
(1)
体系在临界状态时总势能恒为0,则:
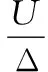
(2)
U和Δ与体系几何位移有关。柔性支撑杆可能存在无限个几何位移,故式(2)的值就不止一个。
弹性曲线方程式对于求解复杂的情况,很难全部满足实际边界条件。故给出下面的曲线方程,拟用含若干参数的变形曲线去逼近真实曲,即:
(3)
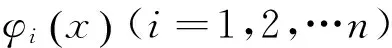
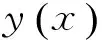
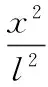
(4)
式中,ai为待定的系数i=1,2;式(4)是假设符合固定端几何边界条件的函数,即:
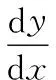
(5)
按式(4)形状函数的选取应确保各柔性支撑杆顶点处的挠度为a1+a2,按式(4)给出的形状函数,柔性支撑杆上任意截面处所受的弯矩M为:
(6)
式中,P为施加在柔性支撑杆顶点处的载荷,L、l分别为柔性支撑杆的刚体长度和柔性长度,θ为支撑杆刚体与x轴之间的夹角。由此可求得杆件的变形能U为:
(7)

计算载荷P作用点沿x轴方向的位移Δ为:
(8)
求得系统总势能Ep为:
EP=U-PΔ
(9)
则可得柔性支撑杆的临界应力Pcr计算公式:
(10)
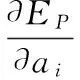
(11)

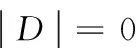
(12)
(13)
将具体数据带入式(13),可以求出临界应力Pcr=minP(上述方程有多个解,取其中最小的一个正解,即1阶失稳,其余解去除)。利用MATLAB编程求解出其最小的P值。
2 有限元屈曲分析
按照上述计算模型,采用有限元软ANSYS14.0对柔性支撑杆进行相应的建模。为了方便分析,结果取最小屈曲临界载荷,即第1阶屈曲临界载荷。
以柔性支撑杆为例,设下端固定、上端为自由端的柔性支撑杆,受上端竖直向下的压力P=888N作用,材料采用铝合金 (7075-O),弹性模量E=72GPa,泊松系μ=0.33,质量密度ρ=2.81g/cm3。D代表支撑杆刚体部分直径,d代表柔性支撑杆的直径。模型参数如表1。

表1 柔性支撑杆尺寸参数
将上述参数带入式(13),MATLAB编程运用SYMS函数,可以解出临界应力Pcr=24405.44N(有3个解,取其中最小的一个正解,其余解去除)。
选用solld185对模型进行网格划分,生成柔性支撑杆有限元模型(如图3):共1757个单元,473个节点。上端面用mass21单元建立耦合刚性面,在中心节点施加集中载荷,使用LANB(分块兰索斯法)进行特屈曲分析如图4所示。

图3 柔性支撑杆有限元模型
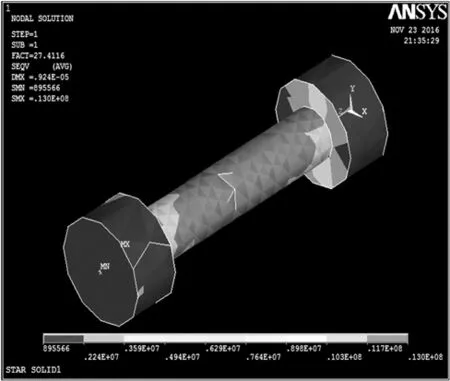
图4 柔性支撑杆屈曲分析
有限元分析结果可得第1阶模态的屈曲载荷系数为27.412,可计算得到有限元分析环境下的屈曲载荷为24341.856N,与精确计算屈曲载荷值相比,差值不超过0.26%,两者结果具有一致性。
3 支撑杆参数与临界载荷的关系
3.1 支撑杆L/l值与临界载荷的关系
分析柔性支撑杆L/l值对屈曲临界载荷的影响,并得出其影响变化规律。分别利用ANSYSY14.0和理论模型对L/l分别为0、0.2、0.5、1、5、10、50的支撑杆进行1阶屈曲分析,数据如表2所示。

表2 不同L/l值下临界载荷及相对误差
表2中Pcr为临界载荷理论计算值,Pcr1为有限元特征值,e为Pcr1与Pcr的相对误差。通过分析表2的数据,可以看出屈曲临界载荷理论计算值与限元分析特征值非常接近,误差不超过3%。对ANSYS求得的1阶屈曲载荷和L/l进行数据处理,得出其影响变化规律,结果如图5所示。
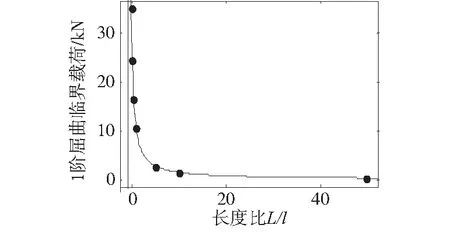
图5 支撑杆L/l值与1阶屈曲载荷的关系
从图5可以看出:柔性支撑杆L/l与其1阶屈曲载荷呈反比例。当L/l从0到1时,下降幅度快,1阶屈曲载荷从34.891kN~10.464kN,下降幅度为70%;当L/l从1~10时,下降幅度慢,1阶屈曲载荷从10.464kN~1.368kN,下降幅度为9.7%;当L/l从10~50时,下降幅度平稳,1阶屈曲载荷从1.368kN~0.261kN,下降幅度为1.6%。可以看出,L/l的变化对1阶屈曲载荷影响极大,因此在柔性支撑杆结构设计时,应充分注意L/l的选择对柔性支撑杆承载力的影响。
3.2 支撑杆D/d值与临界载荷的关系
从柔性支撑杆的截面直径比D/d值影响因素出发,探讨其变化对屈曲临界载荷的影响变化规律。保持柔性支撑杆,其他尺寸参数不变,D/d分别选择0.1、0.2、0.5、1、1.5、2、10、50。利用ANSYSY软件求解1阶屈曲载荷,分析同上,结果如图6所示。
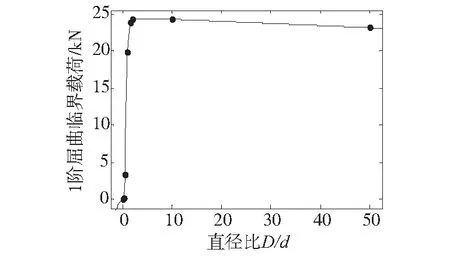
图6 支撑杆D/d值与1阶屈曲载荷的关系
从图6可以明显看出,随着柔性支撑杆D/d的逐渐增加,其1阶屈曲载荷先急剧增加,然后趋于平稳,且有小幅度下降。
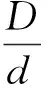
3.3 支撑杆R值与临界载荷的关系
柔性支撑杆是运用普遍和加工工艺比较简单的结构模型,根据以上的分析,这里引入倒角半径R(如图7),对柔性支撑杆进行研究。保持柔性支撑杆,其他尺寸参数不变,R分别为5mm、4mm、3mm、2mm、1mm、0.5mm,为了彻底分析R对临界屈曲载荷的影响,摘取了两极端的倒角半径5mm、0mm。分析方法同上,结果如图8所示。

图7 柔性支撑杆倒角半径R
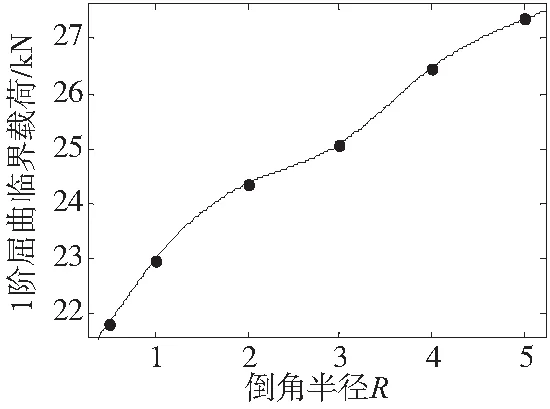
图8 支撑杆R值与1阶屈曲载荷的关系
从图8可以看出: 在保持其他尺寸不变的情况下,仅仅改变R值,柔性支撑杆R值与其1阶屈曲临界载荷呈正相关。当0≤R≤2时,1阶屈曲临界载荷上升幅度较快;当2≤R时,其上升增加但幅度减小。随着R值的增加,其1阶屈曲载荷呈增大趋势,但是R值增加到一定值时,其对1阶临界屈曲载荷的影响在减弱。因此,在对柔性支撑杆结构设计时,在加工工艺锻造水平内,引入倒角半径R,可以大幅度提高稳定性。考虑到结构的加工材料和受力影响,不能无限地增大。
4 结论
本文基于瑞利-里兹能量法,推导计算了精密定位平台柔性支撑杆临界载荷的公式。给其它类型机械关键结构柱杆的稳定性分析提供了一定理论指导意义。同时探讨了柔性支撑杆结构参数对临界载荷的影响,得到结果如下:
(1)随柔性支撑杆L/l增加,支撑杆1阶屈曲载荷下降,呈反比例相关性。当L/l从0~1时,下降幅度为70%,下降最快。随柔性支撑杆D/d逐渐增加,其1阶屈曲载荷先急剧增加,然后趋于平稳,且有小幅度下降;当D/d从2~0.2时,其1阶屈曲载荷锐减99.6%,表明柔性支撑杆D/d值不宜过小。
(2)引入倒角半径R,对柔性支撑杆进行研究,其1阶屈曲载荷随R值的增加而增加,利于实现结构的轻量化设计。
[1]KopeckiT,MazurekP,LisT,etal.Post-bucklingDeformationStatesofSemi-monocoqueCylindricalStructureswithLargeCut-outsUnderOperatingLoadConditions.NumericalAnalysisandExperimentalTests[J].EksploatacjaINiezawodnosc-MaintenanceandReliability, 2016, 18(1):16-24.
[2]ZhangL,WangJ,ZhouYH.Largedeflectionandpost-bucklinganalysisofnon-linearlyelasticrodsbywaveletmethod[J].InternationalJournalofNon-LinearMechanics,2016,78:45-52.
[3]TennysonRC.BucklingModesofCircularCylindricalShellsunderAxialCompression. [J].AiaaJournal, 2015, 7(8):1481-1487.
[4]LaiC,WangJ,LiuC.ParameterizedFiniteElementModelingandBucklingAnalysisofSixTypicalCompositeGridCylindricalShells[J].AppliedCompositeMaterials, 2014, 21(5):739-758.
[5]SahmaniS,BahramiM,AghdamMM.SurfaceStressEffectsonTheNonlinearPostbucklingCharacteristicsofGeometricallyImperfectCylindricalNanoShellsSubjectedtoAxialCompression[J].InternationalJournalofEngineeringScience, 2015, 99(1):92-106.
[6] 张锋, 王三刚, 高致富,等. 新型圆柱杆链柔性纤维模型的建模方法[J]. 中国造纸, 2015, 34(11):48-51.
[7]PaïdoussisMP.DynamicsofCylindricalStructuresSubjectedtoAxialFlow[J].JournalofSound&Vibration, 1973, 29(3):365-385.
[8]PaïdoussisMP,GrinevichE,AdamovicD,etal.LinearandNonlinearDynamicsofCantileveredCylindersinAxialFlow.Part1:PhysicalDynamics[J].JournalofFluids&Structures, 2002, 16(6):691-713.
[9]LopesJL,PaïdoussisMP,SemlerC.LinearandNonlinearDynamicsofCantileveredCylindersinAxialFlow.Part2:TheEquationsofMotion[J].JournalofFluids&Structures, 2002, 16(6):715-737.
[10]SvikS,ThorsenMJ.TechniquesforPredictingTensileArmourBucklingandFatigueinDeepWaterFlexiblePipes[C]//ASME2012,InternationalConferenceonOcean,OffshoreandArcticEngineering,2012:469-482.
[11]JovanovicV,KoshkinS.TheRitzMethodforBoundaryProblemswithEssentialConditionsasConstraints[J].AdvancesinMathematicalPhysics, 2016, 2016(2):1-12.
[12]Arregui-MenaJD,MargettsL,MummeryPM.PracticalApplicationoftheStochasticFiniteElementMethod[J].ArchivesofComputationalMethodsinEngineering, 2016, 23(1):171-190.
[13]CastroSGP,MittelstedtC,MonteiroFAC,etal.EvaluationofNon-linearBucklingLoadsofGeometricallyImperfectCompositeCylindersandConesWithTheRitzMethod[J].CompositeStructures, 2015, 122(122):284-299.
(编辑 李秀敏)
Precision Positioning Platform Flexible Support Bar Buckling Analysis
WU Jian-Jun, WANG Hui, OUYANG Dan, LI Nan, LIAO Tai-jian
(College of Mechanical and Electrical Engineering, Jiangxi University of Science and Technology, Ganzhou Jiangxi 341000, China)
Precision positioning platform for engineering mechanical key structure is common in the structural design of flexible support bar buckling instability problems. First based on Rayleigh Ritz energy variation method, the calculation precision support through building the mathematical model of precision positioning platform flexible support bar buckling critical load and finite element Block Lanczos method for the 1 order before buckling load and buckling mode is compared, the results show that the theoretical value and experimental value deviation is not more than 0.26%, and verified the Rayleigh Ritz energy variation method based on the accuracy of the model. Finally the parameters study on flexible support bar, seeing an inverse proportion in length thanL/landthebucklingcriticalload,thandiameterD/dlessthan1.5influenceonbucklingcriticalloadisbigger,chamferingradiusRandthebucklingcriticalloadisrelated,forthedesignofthepositioningplatformflexiblesupportbarprovidesnewtrainofthought.
flexible support bar; buckling critical load; finite element analysis; reliability
1001-2265(2017)06-0026-04
10.13462/j.cnki.mmtamt.2017.06.007
2017-01-12;
2017-01-20
国家自然科学基金资助项目(51365015,51665017);江西省科技厅科技项目(20142BBE50058,20161BBE80041)
伍建军(1974—),男,四川南充人,江西理工大学副教授,博士,研究方向为工业工程、质量与可靠性研究,(E-mail)391485400@qq.com;通讯作者:汪辉(1993—),男,江西景德镇人,江西理工大学硕士研究生,研究方向为质量与可靠性,(E-mail)2469046602@qq.om。
TH112;TG
A
