基于改进MFCC的鸟鸣声识别方法研究

程龙，张华清

(中国传媒大学 信息工程学院，北京 100024)

基于改进MFCC的鸟鸣声识别方法研究

程龙，张华清

(中国传媒大学 信息工程学院，北京 100024)

鸟鸣声识别的关键就在于对鸣声信号进行合理的特征值提取。鸟鸣声信号具有非平稳性，传统的梅尔倒谱系数(MFCC)仅能反映鸣声信号的静态特性，并且算法中直接运用FFT处理非平稳信号存在局限性。本文提出了一种基于经验模态分解(EMD)改进的MFCC算法，通过对鸟鸣声信号进行经验模态分解，得到一系列固有模态函数分量后再进行FFT计算，频域合成后通过Mel滤波器，取其对数能量进行DCT变换，然后对结果作差分得到改进的MFCC参数，再采用高斯混合模型(GMM)进行鸟鸣声的识别。实验结果表明，改进的MFCC识别率达到70.09%，与未改进的MFCC识别率相比提高了3.42%。

鸣声识别；梅尔倒谱系数；经验模态分解；高斯混合模型

1 引言

鸟类不同于其他物种[1]，具有移动不确定性大、移动范围广的特点，且广泛存在大规模迁徙的习性，其栖息地大部分在丛林，由于植被丰富，树木掩映下时常出现未见其身而只闻其声的状况，因此很难凭借肉眼判断，但是鸟类普遍具有鸣叫的特征，从而使分析鸟类叫声成为了可行的种别辨识手段。

研究表明，和哺乳动物一样，鸟类是用嘴来发出声音的。鸣声发自气管与支气管交界处的特殊发生器：鸣管[2-3]。鸣管由内、外鸣膜、半月膜和鸣肌等组成。鸣膜(亦称鼓膜)是由支气管的软骨短管延长变形、内外侧管壁变薄形成。鸣管正中有一舌状突起，称半月膜。鸣管外侧附着小簇肌肉，称鸣肌，其收缩可控制鸣管的伸缩变形，从而调节进入鸣管的空气量和鸣膜的张力而发出声音。

根据鸟鸣声来识别鸟类的重点就在于分析其鸣声中具有辨识性的成分。鸟类的鸣声也会受到诸如性别、年龄、情绪等的影响，但是同种鸟类的鸣管构造是相似的，不同种类之间却存在差异。常用的鸟鸣声识别方法有时域分析方法和频域分析方法，时域分析方法受限于鸟鸣声样本的选取，难以稳定地获取鸟鸣声特征来加以识别。已有多位学者在对鸟鸣声进行识别时采用频域分析方法，其中应用最多的就是MFCC分析方法[4-6]。

鸟鸣声信号具有非平稳性，传统的MFCC仅能反映鸣声信号的静态特性并且算法中直接运用FFT处理非平稳信号存在局限性。本文提出了一种基于EMD[7-8]改进的结合差分的MFCC算法，对鸟类鸣叫声进行特征提取，并结合高斯混合模型进行鸟鸣声的识别。

2 MFCC特征提取

对于语音信号来说，倒谱参数所包含的信息较其他参数多，它是目前普遍采用的说话人特征参数。倒谱系数反映了声道的共振性能。常用的倒谱系数有：线性预测倒谱系数(LPCC)和Mel倒谱系数(MFCC)。与LPCC不同的是，MFCC的分析着眼于人耳的听觉机理[9-11]，依据听觉实验结果来分析语音的倒谱，获得了较高的识别率和较好的噪声鲁棒性。将MFCC应用在鸟鸣声识别上就是为了剔除其他因素的影响，保留鸣管的发声特性。

MFCC是在Mel标度频率域提取出来的倒谱参数，Mel标度描述了人耳频率的非线性特性，它与频率的关系可用下式近似表示：

(1)

MFCC的计算过程如图1所示。

图1 MFCC计算过程

MFCC的具体计算步骤如下：

(1)对输入的声音信号进行预加重，分帧，加窗等预处理。

(2)对帧信号做快速傅立叶变换(FFT)：

(2)

(4)对每个滤波器的输出取对数，得到相应的对数能量。

(5)将Mel滤波器组输出的对数能量进行离散余弦变换(DCT)，得到MFCC倒谱系数：

(3)

传统的MFCC仅能反映鸣声信号的静态特性，而鸣声信号的动态特性可以用这些静态特征的差分来描述。差分MFCC倒谱系数Dn的计算公式为：

(4)

其中k为常数，一般取2。

3 改进的MFCC特征提取

3.1 经验模态分解

经验模态分解(EMD)即EMD法，是美国工程院士黄锷博士于1998年提出的一种信号分析方法，特别适用于非线性非平稳信号的分析处理。而鸟鸣声信号具有明显的非平稳性，故EMD分解能够适用于鸟鸣声信号的分析与处理。

黄锷等人认为任何信号都是由若干本征模函数组成，任何时候，一个信号都可以包含若干个本征模函数，如果本征模函数之间相互重叠，便形成复合信号。EMD分解的目的就是为了获取本征模函数(IMF)，一个IMF必须满足以下两个条件：

(1)在整个信号序列内，局部极值点和过零点的数目必须相等或最多相差一个。

(2)在任意时刻点，由局部最大值构成的包络(上包络线)和由局部最小值构成的包络(下包络线)的平均值必须为零。

EMD分解流程如图2所示。

图2 EMD分解流程

EMD具体分解步骤如下：

(1)确定信号序列x(n)中所有的极大值点和极小值点。

(2)用三次样条线分别拟合原序列的上包络线和下包络线。

(3)求出上下包络线的均值为m(n)，并计算差值h(n)=x(n)-m(n)。

(4)判断h(n)是否符合IMF条件，如不符合则将h(n)作为信号序列输入，重复上述过程，如此循环直到得到第一个IMF分量e(n)。

在得到第一个IMF分量后，将信号序列减去分量重复上述步骤，得到第二个IMF分量，这样不断重复直到得到所有IMF分量。

图3表示对预处理后的金黄鹂鸣声信号进行EMD分解的结果，分解得到六个IMF分量和一个残余分量。E1到E6为IMF分量，E7为残余分量。其频率从高到低排列，E1频率最高，E6最低，E7为残余项。可见EMD分解可以完全体现鸣声信号的变化。

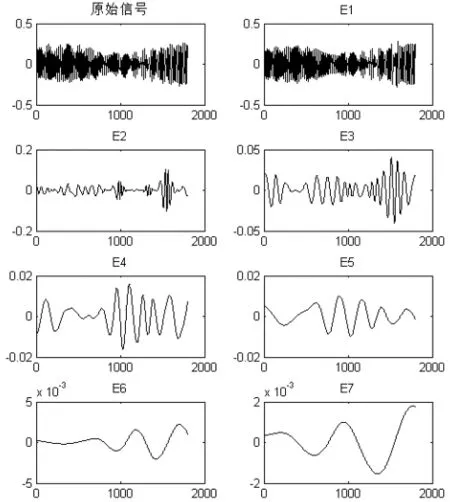
图3 金黄鹂鸣声经EMD分解后的结果

3.2 改进的MFCC

相比传统的MFCC特征提取算法，改进的MFCC特征提取流程如图4所示。首先对鸟鸣声信号进行预加重，分帧，加窗等预处理；然后对每帧鸟鸣声信号进行EMD分解，得到多个频率由高到低的IMF分量，接着对每个IMF进行FFT变换；分别计算各个IMF分量的能量谱，频域合成后通过Mel滤波器组滤波；然后对Mel滤波器组的输出取对数，进行DCT变换，得到静态MFCC系数；对静态MFCC作差分，得到动态MFCC系数；最后将静态MFCC系数与动态MFCC系数结合便是改进的MFCC。

图5是同一帧苍头燕雀鸣声信号的不同MFCC算法的特征参数对比图。传统MFCC取12维系数作为特征参数，结合差分的MFCC特征参数为24维，可以看出前12维特征参数相同，但是后者还包含了12维动态特性。本文改进的MFCC为24维，并且每一维度的值都与未用EMD改进的结合差分的MFCC不同，其中前12维静态参数更加平滑，而后12维动态参数变化更明显。

图4 改进的MFCC计算过程

图5 苍头燕雀鸣声的不同特征参数

4 实验结果与分析

本文所用鸟鸣声样本均来自XC网站(www.xeno-canto.org)。考虑到鸣声样本获取的难易度和地理位置等因素，选择我国西南地区常见的暗绿柳莺、八声杜鹃、苍头燕雀、大尾莺、黑胸麻雀、金黄鹂和紫水鸡等7种鸟类一共594个鸣声样本。其中暗绿柳莺157个，八声杜鹃83个，苍头燕雀78个，大尾莺108个，黑胸麻雀61个，金黄鹂62个，紫水鸡45个。

仿真实验过程中，每种鸟类60%的鸣声样本作为训练样本，40%的鸣声样本作为测试样本。本文选择GMM模型分类器[12-14]对提取的特征参数进行训练。分别在传统MFCC、结合差分的MFCC和改进的MFCC三种不同特征提取方法下进行鸟鸣声识别实验。传统MFCC的识别率见表1，结合差分的MFCC的识别率见表2，本文提出的改进MFCC的识别率见表3。

对比表1和表2可知，结合差分的MFCC的鸟鸣声总体识别率较传统MFCC有提高，提高了3.85%，但是在个别鸟类鸣声识别率上反而有所下降。这表示虽然结合差分的MFCC引入了动态特性，然而并不能稳定的提升鸟鸣声识别率。

对比表2和表3可知，本文提出的改进MFCC的鸟鸣声总体识别率比结合差分的MFCC的总体识别率提高了3.42%，比传统MFCC则提高了7.27%，并且没有出现个别鸟鸣声识别率下降的情况。黑胸麻雀的鸣声识别率低于其他鸟类，是因为黑胸麻雀喜群居生活，XC网站上所录制的音频样本存在多只黑胸麻雀同时鸣叫的情况。

表1 传统MFCC的识别率(%)

表2 结合差分的MFCC的识别率(%)

续表

表3 改进MFCC的识别率(%)

5 结束语

鸟鸣声信号具有非平稳性，传统的梅尔倒谱系数(MFCC)仅能反映鸣声信号的静态特性并且算法中直接运用FFT处理非平稳信号存在局限性。针对上述问题，本文提出了一种基于EMD改进的结合差分的MFCC算法，对鸟类鸣叫声进行特征提取并配合GMM模型分类器对鸟鸣声进行识别。实验结果表明，改进MFCC的鸟鸣声识别方法的识别率达到70.09%，比未改进的鸟鸣声识别方法的识别率提高了3.42%。下一步工作就是对该方法的实用性和鲁棒性进行研究。

[1]杨勇，温俊宝，胡德夫. 鸟类栖息地研究进展[J]. 林业科学，2011，47(11)：172-180.

[2]李东风，蓝书成. 鸟类鸣叫学习机理研究回顾[J]. 生理科学进展，1991，(4)：324-328.

[3]吕琳娜. 鸟类鸣声初探[J]. 生物技术世界，2016，(5)：93-93.

[4]王恩泽，何东健. 基于MFCC和双重GMM的鸟类识别方法[J]. 计算机工程与设计，2014，35(5)：1868-1871.

[5]伟利国，张小超，吴文彪. 鸟鸣叫声特征提取方法的研究[J]. 辽宁师范大学学报(自然科学版)，2010，33(1)：108-111.

[6]戴天虹，李野，孙鹏. 基于MATLAB鸟叫声特征提取方法的研究[J]. 森林工程，2013，29(2)：130-134.

[7]Huang N E，Shen Z，Long S R. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society A Mathematical Physical & Engineering Sciences，1998，454(1971)：903-995.

[8]Colominas M A，Schlotthauer G，Torres M E. Improved complete ensemble EMD：A suitable tool for biomedical signal processing[J]. Biomedical Signal Processing & Control，2014，14(1)：19-29.

[9]S Nakagawa，L Wang，S Ohtsuka.Speaker Identification and Verification by Combining MFCC and Phase Information[J].IEEE transactions on audio，speech，and language processing，20，2012.

[10]M A Hossan，S Memon，M A Gregory.A novel approach for MFCC feature extraction[J].Signal Processing and Communication Systems(ICSPCS)，2010.

[11]朱春媚，黎萍. 基于子带能量变换改进MFCC的咳嗽识别[J]. 计算机工程与应用，2016，52(11).

[12]V R Apsingekar，P L De Leon.Speaker Model Clustering for Efficient Speaker Identification in Large Population Applications[J].IEEE transactions on audio，speech，and language processing，17(4)：848-853，2009.

[13]S K Biswas，D P Mukherjee.Recognizing Architectural Distortion in Mammogram：A Multiscale Texture Modeling Approach with GMM[J].IEEE Transactions on Biomedical Engineering，58(7)，2011.

[14]Haipeng Wang，Xiang Zhang，HongbinSuo，Qingwei Zhao，Y Yan.A novel fuzzy-based automatic speaker clustering algorithm[J].ISNN ，639-646，2009.

(责任编辑：宋金宝)

Research of Birdsong Recognition Method Based on Improved MFCC

CHENG Long，ZHANG Hua-qing

(Information Engineering School，Communication University of China，Beijing 100024，China)

To choose a proper feature extraction method is the key of birdsong recognition. The signals of birdsong are non-stationary.The conventional Mel-Frequency Cepstral Coefficients(MFCC)can only reflect signals’ static features and has a certain limitation to use FFT to process the signals directly. In this paper，an improved MFCC algorithm is raised on the basis of Empirical Mode Decomposition(EMD).FFT is used after divided signals of birdsonginto intrinsic mode functions with EMD. The next steps are frequency synthesis，Mel filtering，logarithm and DCT. In the end，the improved MFCC parameters are obtained by doing differential calculation of the DCT results. The birdsongs can be recognized through the Gaussian Mixture Model(GMM). The results show that the recognition rate of the improved MFCC is 70.09%，and the recognition rate is increased by 3.42% compared with the conventional MFCC.

birdsong recognition；Mel-Frequency Cepstral Coefficients(MFCC)；Empirical Mode Decomposition(EMD)；Gaussian Mixture Model(GMM)

2016-11-15

程龙(1988-)，男(汉族)，江西南昌人，中国传媒大学硕士研究生. E-mail：552151607@qq.com

TN912.3

A

1673-4793(2017)03-0041-06