一类无限维李代数的双导子

黄晶晶，张志兰，付佳媛

(中国传媒大学 理工学部，北京100024)

一类无限维李代数的双导子

黄晶晶，张志兰，付佳媛

(中国传媒大学 理工学部，北京100024)

本文给出了一类与Virasoro代数相关的无限维李代数，详细刻画了该类李代数的双导子结构与性质，并且得到该类李代数上的线性交换映射的形式。

Virasoro代数；代数导子；双导子；线性交换映射

1 前言

在李代数的领域里，导子与广义导子的结构与性质是比较重要的课题。Virasoro代数[1]是一类非常著名的无限维李代数，在物理与数学的许多分支里具有广泛的应用，许多学者对其结构已经做了细致而深刻的研究。双导子与线性交换映射是近年来比较热门的方向，例如对Schrödinger-Virasoro 李代数，以及Super-Virasoro代数的双导子的计算。文献[2] 中，Schrödinger-Virasoro代数的双导子与线性交换映射的问题得到了解决。在文献[3]中，作者定义了W(a，b)代数上所有斜对称双导子，并且发现了外双导子的存在。双导子同时适用于超代数上，其被称作超双导子，文献[4]表明Super-Virasoro代数上的斜对称超双导子也是内双导子。有了这些作者们积极的探索，将有助于我们刻画出一类与Virasoro代数相关的无限维李代数的双导子结构，并得出比较好的性质。

2 预备知识

在本文中，我们用G表示一般的李代数，S表示一类无限维李代数，表示整数，表示复数域。

定义2.1[5]对任意的李代数G，定义一个线性映射D：G→G，如果对∀x，y∈G，D满足以下条件：

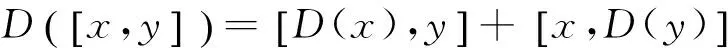
我们就称D是G的导子。

定义2.2 对李代数G，定义一个双线性映射δ：G×G→G，我们称δ为G的双导子，如果对∀x，y，z∈G，满足以下关系式：

其中m，n，p，q∈。

引理2.4[6]Der(S)/Inn(S)=0，也就是说，李代数S的每一个导子D都可以写做D=adx，其中x∈S。

3 李代数S的双导子

这一部分当中，我们将逐步讨论得到李代数S的双导子结构，在此仍然用δ表示S的双导子。

定理3.1若δ是李代数S的双导子，则：

δ(x，y)=[φ(x)，y]=[x，ψ(y)]，∀x，y∈S

其中φ，ψ是两个线性映射：

φ：S→S

ψ：S→S

证明：以下分两步来证明该定理：

(1)对于S中的某一个元素x，我们定义映射：φx：S→S，使得

δ(x，y)=φx(y)，任取a，b，c∈S，由于：

δ(a，[b，c])=φa([b，c])，

[δ(a，b)，c]+[b，δ(a，c)]=[φa(b)，c]+[b，φa(c)]

显然易证φx是S的导子，又由引理2.4知S的导子都是内导子，故存在映射φ，φ：S→S，使得φx=adφ(x)。那么φx(y)=ad(φ(x))(y)=[φ(x)，y]，即证δ(x，y)=[φ(x)，y]。又由于δ是双线性映射，则φ一定是线性映射。

(2)相似地，我们定义一个映射ψy：S→S，使得ψy(x)=δ(x，y)，ψy是S中的内导子，同样存在映射ψ：S→S，使得ψy=ad(-ψ(y))，那么δ(x，y)=ψy(x)=ad(-ψ(y))(x)=[x，ψ(y)]。

定理3.2李代数S的双导子都是内双导子。

我们将该定理的证明分为以下两个引理。

引理3.3存在μ∈，使得

φ(Ln)=μLn，ψ(Ln)=μLn

φ(Mn)=μMn，ψ(Mn)=μMn

φ(Yn)=μYn，ψ(Yn)=μYn

其中n∈。φ：S→S，ψ：S→S

证明：设对任意的m∈，有

(1)

(2)

(3)

其中，i∈，

鉴于接下来的运算量比较大，为了方便起见，我们分以下四步来讨论：

第一步，将(1)式代入，通过直接运算得到：

(4)

(5)

(6)

(7)

(8)

对(6)式，

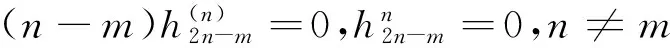
综上，令m，n取遍m≠n的所有整数，得到：

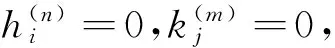
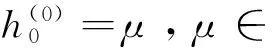
对(7)式，

对(8)式，

以下是m，n不全为偶数的情况：

当m为偶数，n为奇数时，令n=2k+1，m=2l，k，l∈，代入到(8)式中去，有

综合上述所得到的结果，可得到：

(9)

第二步，

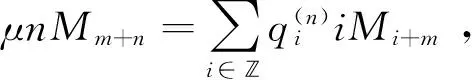
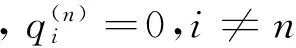
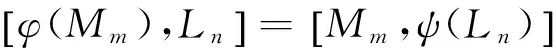
(10)

(11)

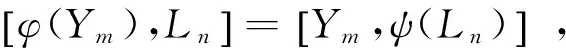
将所得的结果代入到(9)(11)式中，可知：

从而该引理得证。

引理3.4若δ是李代数S的双导子，当且仅当δ是李代数S的内双导子，也就是说存在μ∈使得∀x，y∈S。

证明：若δ是李代数S的内双导子，显然易证δ是李代数S的双导子。反过来，若δ是李代数S的双导子，由引理3.3知，φ(x)=μx，ψ(y)=μy，μ∈，又由定理3.1知δ(x，y)故

4 线性交换映射

定理4.1若φ是无限维李代数S上的线性交换映射，当且仅当存在复数μ使得φ(x)=μx，x∈S。

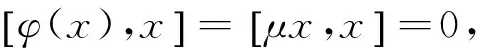
[1]YucaiSu，KaimingZhao.GeneralizedVirasoroandsuper-Virasoroalgebrasandmodulesoftheintermediateseries[J].JournalofAlgebra， 2002.

[2]Wang D，Yu X. Biderivations and linear commuting maps on the Schrödinger-VirasoroLie algebra[J]. Communications in Algebra，2013，41(6)：2166-2173.

[3]Han X，Wang D，Xia C. Linear commuting maps and biderivations on the Lie algebras W(a，b)[J]. Journal of Lie theory，2016，26(3)：777-786.

[4]Xia C，Wang D，Han X. Linear super-commuting maps and super-biderivations on the super-Virasoro algebras[J]. Communications in Algebra，2016，44(12)：5342-5350.

[5]苏育才，卢才辉，崔一敏.有限维半单李代数简明教程[M].北京：科学出版社，2008.

[6]吕彦玮，朱林生.一类李代数的导子代数[J].常熟理工学院学报(自然科学版)，2011，25(2).

[7]Bregar M.Commuting maps：a survey[J].Taiwanese Journal of Mathematics，8(3)：361-397，2004.

(责任编辑：宋金宝)

Biderivation of a Class of Infinite-dimensional Lie Algebra

HUANG Jing-jing，ZHANG Zhi-lan，FU Jia-yuan

(Faculty of Science and Technology，Communication University of China，Beijing 100024，China)

A class of infinite-dimensional Lie algebra related to Virasoro algebra is introduced in this paper，we research its biderivation structure clearly and then the property is determined. Besides，we get the forms of linear commuting map on the algebra.

Virasoro algebra；derivation；biderivation；linear commuting map

2016-12-05

黄晶晶(1990-)，女(汉族)，山东菏泽人，中国传媒大学硕士研究生.E-mail：1543460315@qq.com

O152.5

A

1673-4793(2017)03-0063-06