应用COMSOL对二维三角晶格光子晶体带隙仿真

张雁茗，逯贵祯

(中国传媒大学，北京 100024)

应用COMSOL对二维三角晶格光子晶体带隙仿真

张雁茗，逯贵祯

(中国传媒大学，北京 100024)

介绍了一种使用COMSOL用数值计算方法仿真2D光子晶体色散图的方法，通过COMSOL将Z方向无限延伸的介质介质圆柱阵列形成的二维三角晶格光子晶体等效为二维平面进行仿真，并采用了独特的矩形结构作为该三角晶格光子晶体的单元晶格，相比传统的用正六边形作为单元晶格的方法，建模与设置Floquet周期边界条件的过程更为简单。成功仿真出了该光子晶体的色散图，并与参考文献中的结果进行了对比分析，带隙、色散曲线与文献中结果基本吻合，证明了这种仿真方法的正确性。

光子晶体；光子带隙；色散图；三角晶格；COMSOL

1 引 言

光子晶体是由不同介电常数的介质材料在空间中呈周期排布的结构，当电磁波在介电常数周期性排列的光子晶体中传播时可产生使某些频率的电磁波无法传播的的光子带隙，即特定频率范围的电磁波无法在光子晶体中传播[1]。

二维光子晶体为两种及两种以上电介质材料在空间中呈二维周期性排列的结构，其晶格常数与光波或电磁波波长相当。目前，二维光子晶体晶格多采用四方晶格，三角晶格、六角晶格[1]。其中三角晶格受制造不均匀性的影响最小，比较容易实现较为完整的光子带隙。要在三角晶格中得到完整的带隙，必须保证足够的空隙率，即r/a(r为介质柱半径，a为相邻介质柱最小中心距离)。除此之外，介质柱的形状对带隙的结构也有影响，横截面为圆形、三角形、四边形的介质柱所形成的带隙结构中，其中圆柱型介质柱形成的光子晶体具可以产生有较为显著的带隙。

仿真二维光子晶体带隙的常用方法为平面波展开法，应用Matlab软件编写出计算程序之后对光子晶体进行模拟计算。本文使用了仿真软件COMSOL，通过数值计算方法来对其进行建模与仿真。COMSOL的二维建模功能可以将在空间中延z方向无线延伸的三角介质柱阵列形成的二维光子晶体等效为在xoy平面上的周期结构进行仿真。以往应用仿真软件对三角晶格光子晶体进行建模时，通常方法为选取一个正六边形结构作为单元晶格，并通过周期拓展来等效三角晶格光子晶体阵列。本文在对三角晶格光子晶体的仿真过程中采用了独特的矩形单元晶格划分方法，使得建模更为简单，且单元晶格的周期边界是正交的，仅通过对X、Y两个方向的Floquet周期边界条件的设定，便可以等效三角晶格光子晶体的周期结构，以Bloch波矢k作为特征值[2]，计算了由介质构成的三角晶格光子晶体的能带结构，并通过对比参考文献中的结果，验证了该方法的正确性和有效性。

2 三角晶格光子晶体结构及其布渊区

图1是由介质柱周期排列构成的三角晶格光子晶体阵列，其在z方向无限延、半径r= 0.6、间距a=4(杆的中心之间的距离)、折射率n=2.9，背景介质为空气。

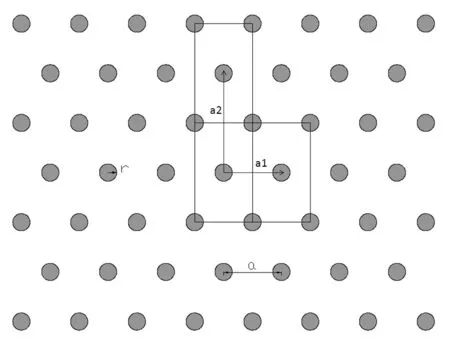
图1 光子晶体晶格单元图

图2 矩形晶格单元

每个晶体都有两种晶格，即真实空间中的晶格和倒易空间的晶格。平面正三角形晶格相邻原子间距为a，则三角晶格在正空间的基矢量：

由于将三维模型等效为二维平面，可将其中基矢量c被假定为单位向量ez，则倒格子的基矢量为：

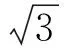
选取一个倒格点为原点，距原点最近的倒格子基矢量有6个，分别为：±A，±B，±(A+B)

由6个基矢量可以得出该三角晶格光子晶体的第一布里渊区如图3所示[3]，其中三角形区域ΓJX为三角晶格光子晶体的不可约布里渊区，其三个顶点坐标分别为：

Γ=2π/a(0，0)

J=2π/a(2/3，0)

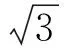
图3 第一布里渊区

3 仿真结果对比与分析

如图4所示，是选取矩形单元晶格情况下仿真得到的2D光子晶体色散图，该结果显示1 /λ=ω/(2πc)在0.1和0.14之间存在着明显的带隙，其结果与图5参考文献[4]中的结果基本吻合(考虑到与文献中使用不同的计算方法造成仿真结果使得高频模式存在细微误差，该误差不影响对带隙的分析)

图4 三角晶格2D光子晶体色散图

图5 参考文献中的色散图[4]

4 结论

同目前其他学者采用的方法相比[5-9]，本文的建模方法为选取矩形单元结构作为三角晶格光子晶体的单元晶格，由于边界条件是正交的，通过软件COMSOL设定Floquet周期边界条件的过程更为简便，进行周期拓展等效出三角晶格光子晶体阵列，并成功仿真出了该光子晶体的色散图，仿真结果经对比后与文献[4]中结果基本一致，证明了这种建模与仿真方法的可行性。

[1]马锡英.光子晶体原理及应用[M].北京：科学出版社，2010.

[2]谢处方，饶克谨.电磁场与电磁波 [M].北京：高等教育出版社，2015.

[3]黄昆.固体物理学[M].北京：北京大学出版社，2014.

[4]EnochS，TayebG，MaystreD.DispersionDiagramsofBlochModesAppliedtotheDesignofDirectiveSources[J].ProgressinElectromagneticsResearch，2003，41(1)：61-81.

[5]冯帅，杨笛，陈笑，等.二维三角晶格介质柱光子晶体的完全光子禁带[J].中央民族大学学报(自然科学版)，2009，18(3)：33-38.

[6]牛凯坤，王丽华，黄志祥，等.三角晶格有耗色散光子晶体的能带结构分析[J].光子学报，2016，45(3)：56-61.

[7]YangHYD，AlexopoulosNG，YablonovitchE.Photonicband-gapmaterialsforhigh-gainprintedcircuitantennas[J].IEEETransactiononAntennas&Propagation，1997，(1)：185-187.

[8]PlihalM，MaradudinAA.Photonicbandstructureoftwo-dimensionalsystems：Thetriangularlattice.[J].PhysicalReviewBCondensedMatter，1991，44(16)：8565-8571.

[9]SmithGS，KeslerMP，MaloneyJG.Dipoleantennasusedwithall-dielectric，woodpilephotonic-bandgapreflectors：Gain，fieldpatterns，andinputimpedance[J].Microwave&OpticalTechnologyLetters，2015，21(3)：191-196.

(责任编辑：王谦)

Application of COMSOL to Band Gap Simulation of Two-dimensional Triangular Lattice Photonic Crystals

ZHANG Yan-ming，LU Gui-zhen

(Communication University of China，Beijing 100024，China)

A method of simulating 2D photonic crystal dispersion by using COMSOL numerical simulation method is introduced.The two-dimensional triangular lattice photonic crystal formed by the cylindrical array of Z-direction infinite extension is equivalent to a two-dimensional plane by COMSOL.Using the unique rectangular structure as the lattice of the triangular lattice photonic crystal，it is simpler to model and set the Floquet periodic boundary condition than the traditional method of using the regular hexagon as a lattice.The dispersion diagram of the photonic crystal was successfully simulated and compared with the results in the reference.The bandgap and dispersion curves were consistent with the results in the literature，which proved the correctness of the simulation method.

photonic crystal；photonic band gap；dispersion diagram；triangular lattice；COMSOL

2017-03-07

张雁茗(1994-)，男(汉族)，辽宁沈阳人，中国传媒大学硕士研究生.E-mail：424193064@qq.com

O

A

1673-4793(2017)03-0031-03