带有阻尼机构的多柔体航天器动力学建模
2017-07-05朱孟萍陈新龙
朱孟萍,耿 磊,陈新龙,李 志
(中国空间技术研究院钱学森空间技术实验室,北京 100094)
带有阻尼机构的多柔体航天器动力学建模
朱孟萍,耿 磊,陈新龙,李 志
(中国空间技术研究院钱学森空间技术实验室,北京 100094)
对通过阻尼机构连接的多柔体航天器动力学问题进行研究,考察的系统由航天器本体、若干六自由度刚性阻尼平台以及固连于阻尼平台的大柔性附件构成,阻尼平台与航天器本体之间以弹性-阻尼装置连接,为典型的多柔体系统.以混合坐标描述系统的运动,利用Kane方程建立了具有较强通用性且有利于系统控制器设计的含有约束阻尼的动力学模型.数值仿真结果表明,阻尼器可有效衰减柔性附件的振动,有利于星体受扰后的快速稳定. 关键词: 柔性附件;阻尼器;动力学;Kane方程
0 引 言
由于现代航天任务的需要,许多航天器都带有大型柔性附件,例如大型太阳帆板、大型柔性天线以及天线支撑臂等.由于航天器柔性附件结构阻尼一般很小(0.001~0.005),其振动自然衰减很慢,使得柔性附件上的一些有效载荷的指向准确性难以有效保证.
在航天器本体与柔性附件之间使用阻尼器则可以使得柔性附件的振动能量以耗散能的形式释放,从而使得附件振动有效衰减.美国的SRTM(shuttle radar topography mission)就是在60 m长的柔性支撑臂的根部加装了阻尼器,从而提高支撑臂端部天线的指向精度以及航天飞机的姿控精度[1-3].
目前大型应用卫星的整星动力学建模方法是混合坐标法,基于这种方法针对其构形特征所建立的中心刚体加柔性附件类航天器动力学模型,要求中心体的转动惯量和质量远远大于柔性附件的转动惯量和质量,其控制对象为星本体的指向与稳定度,对柔性附件的处理主要考虑其振动对中心刚体指向和稳定度的影响.本文研究的对象背景是带有长天线支撑臂天基干涉SAR卫星,星上带有大型太阳阵和长度为60~80 m的柔性天线伸展臂,整星规模庞大,构形复杂,中心体的转动惯量仅占整星转动惯量的百分之五左右.该卫星的控制要求不仅是中心刚体的指向与稳定度,更重要的是天线支撑臂形成的干涉基线矢量的指向及稳定度.因此,基于中心刚体加柔性附件的混合坐标法不适用于该类卫星的动力学建模.
此类航天器动力学属于多体系统动力学问题.尽管已有诸多研究者对该类航天器动力学进行了深入广泛的研究,但研究对象中柔性附件通常是固接或铰接(三自由度)于航天器本体上[4-7].本文则以更为通用的带有六自由度柔性附件阻尼器的航天器系统为研究对象,利用Kane方程建立系统的动力学模型,并对姿态运动受扰后的动力学响应进行了数值仿真与分析.
1 系统描述与坐标系定义
为了简要清晰地论述本文研究的主要问题,图1 给出了简化的系统构型与坐标系示意图.
所研究的系统由刚性航天器本体、n个六自由度刚性阻尼平台以及固连于阻尼平台的柔性附件构成.刚性阻尼平台与航天器本体之间以若干弹性-阻尼装置连接,相对本体可具有六个运动自由度.柔性附件固连于阻尼平台上.在后续的动力学建模与仿真中忽略弹性-阻尼装置的质量和惯量特性,仅考虑其作用力.
为描述系统运动,定义如下坐标系:
(1)惯性坐标系FI(OXYZ):
原点位于地球中心O,Z轴沿地球极轴指向北极,X轴指向春分点,Y轴与X、Z轴构成右手坐标系,其单位基向量为eI=[eIxeIyeIz]T;
(2)航天器本体坐标系Fb(obxbybzb):
原点位于航天器本体质心ob,xb、 yb轴与zb轴为本体惯性主轴,且构成右手坐标系,其单位基向量为eb=[ebxebyebz]T;
(3)阻尼平台i体坐标系Fdi(odixdiydizdi):
原点位于阻尼平台i的质心odi,xdi、 ydi轴与zdi轴为阻尼平台i的惯性主轴,且构成右手坐标系,其单位基向量为edi=[edixediyediz]T;
(4)柔性附件i体坐标系Fai(oaixaiyaizai):
原点oai位于柔性附件i与阻尼平台i的连接处,xai、 yai轴与zai轴与柔性附件i固连,且构成右手坐标系,其单位基向量为eai=[eaixeaiyeaiz]T.
2 系统的运动学关系
首先定义下述矢径:
定义下述角速度矢量:
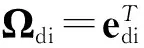
由上述各矢径定义可知,各体质量参考点在惯性坐标系中的矢径分别为
(1)航天器本体
(1)
(2)阻尼平台i(i=1,2,…,n)
(2)
(3)柔性附件i(i=1,2,…,n)
(3)
对式(1)~式(3)分别求时间导数可得各体质量参考点相对惯性系的速度为:
(1)航天器本体
(4)
(2)阻尼平台i(i=1,2,…,n)
(5)
(3)柔性附件i(i=1,2,…,n)
(6)
进一步对式(4)~(6)求时间导数可得各体质量参考点相对惯性系的加速度为
(1)航天器本体
(7)
(2)阻尼平台i(i=1,2,…,n)
(8)
(3)柔性附件i(i=1,2,…,n)
(9)
以3-1-2旋转顺序的欧拉角描述航天器本体相对惯性坐标系的姿态,则其运动学关系为
(10)
式中
其中φ、θ和ψ分别为航天器相对惯性系的滚动角、俯仰角和偏航角.若以同样旋转顺序的欧拉角描述阻尼平台i相对其标称位置的方位角,则有
(11)
式中Θdi、Tdi(Θdi)分别与Θ、Tb(Θ)具有类似的形式.
3 Kane方程的基本形式
Kane方程可以写为如下形式:
(12)
对于连续弹性体B,以上各量的计算过程如下[8]:
(13)
则
(14)
(15)
(16)

对于本文所研究的多体系统,也要先按各体分别计算,然后再求和.例如对于广义惯性力,应为:
(17)
式中各下标的含义是:第一个下标“I”表示广义惯性力,第二个下标表示它是与偏速度Wh对应的第h阶广义惯性力,第三个下标则是表示它是属于哪个体的.
4 偏速度与系统动力学方程
将柔性附件i的质量参考点的弹性位移写为如下形式:
dai=Naiqai
(18)
其中,Nai为相应的变形基函数矩阵,与柔性体各点位置有关,一般可取为弹性体的模态函数,qai为柔性体的广义坐标列阵,与时间有关,一般则可取为与模态函数对应的模态坐标.相应的弹性变形的速度和加速度则为:
(19)
选取各阶偏速度如下:

Wn+3=ωd1,…,W2n+2=ωdn,

根据如上选取的偏速度,结合系统中各体参考点的速度与加速度表达式,按照Kane方程的推导过程,最后可得到对应于各偏速度的动力学方程如下
(20)
(2)航天器本体转动方程(对应于偏速度ω)
(21)
(22)
(4)阻尼平台i的转动方程(对应于偏速度ωdi)
(23)
(24)
式中,Fb为作用于航天器本体的力,Tb为作用于航天器本体的力矩,均在航天器本体坐标系中描述;Fdi和Tdi则分别为阻尼平台i受到的弹性-阻尼装置的力和力矩,Fdi在航天器本体坐标系中描述,Tdi在阻尼平台i的体坐标系中描述.各方程右端的Q*项为非线性耦合项.方程左端各系数矩阵及方程右端的各非线性耦合项的表达式不再一一给出.
式(20)~式(24)还可以写为如下的统一形式:
(25)
式中,



X=[RΘS1Θd1qa1…SnΘdnqan]T,
F=[AIbFbTbFd1Td10 …FdnTdn0]T,
Q=[QRQΘQSd1QΘd1Qqa1…QSdn
QΘdnQqan]T.
M为系统的质量阵,为对称正定阵;K为系统的刚度阵.Fdi和Tdi的表达式与阻尼装置的具体结构相关.依据不同阻尼装置的具体结构可建立Fdi和Tdi的不同表达式,以应用于不同的系统.若阻尼平台在六个运动自由度上均具有线性解耦的刚度和阻尼形式,则有
(26)
(27)
其中KSdi和CSdi分别为平动刚度和阻尼对角阵,KΘdi和CΘdi分别为转动刚度和阻尼对角阵.
从以上系统的质量阵可以看出,加入阻尼平台后,质量阵除主对角元素以外的元素增多,整个系统,除了柔性附件与航天器本体之间的耦合外,还增加了阻尼平台与航天器、阻尼平台与柔性附件之间的耦合,整星耦合系数增大.当阻尼平台的刚度和阻尼如式(26)(27)所示时,系统的刚度矩阵等效为:
K′=
该等效刚度矩阵K′和系统质量阵M直接决定了整个航天器的系统频率,因此,在引入阻尼平台后,通过调节其刚度系数KSdi和阻尼系数KΘdi来调节整个航天器的系统频率,与姿态控制系统协调,共同实现整个系统的控制任务要求.
5 数值仿真与分析
数值仿真中采用的航天器模型由卫星本体、一个六自由度刚性阻尼平台和一个柔性梁结构组成,如图2所示.表1给出了系统中各体的质量及惯量参数.
阻尼平台标称位置为rb,d=[0 0.5 1.3]Tm,柔性梁的安装位置为rd,a=[0 0.5 0]Tm.利用有限元方法对柔性梁进行了模态分析,其基频为0.099Hz.仿真中取其前六阶模态,经计算可知,前六阶模态的模态质量占其总质量的86.56%,模态惯量占其总惯量的99.58%,因此前六阶模态已具有很高的惯性完备性.
仿真中假定阻尼平台具有如式(26)和(27)所示的线性解耦的刚度和阻尼形式,相关参数取为
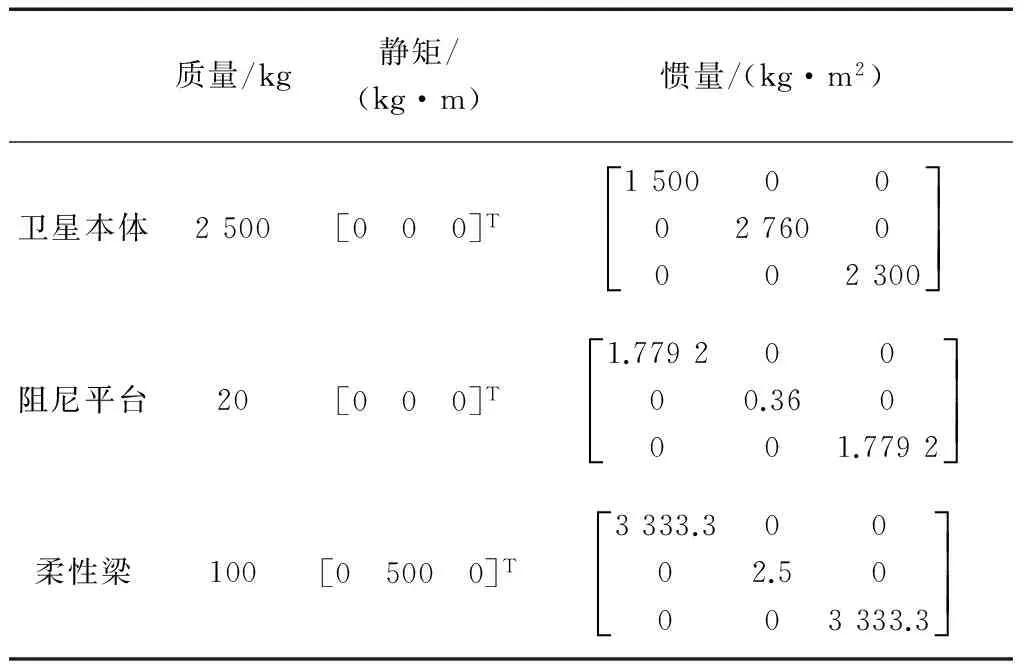
KSd=diag{233,120,233} N/m,KΘd=diag{161,161,101} (N·m)/radCSd=diag{270,150,270} (N·s)/m,CΘd=diag{298,298,177} (N·m·s)/rad表1 各体质量及惯量参数Tab.1 The mass and inertia parameters of each body
仿真中不考虑轨道运动,对卫星本体滚动轴和偏航轴施加如图3所示的正弦扰动力矩,考察系统的动力学响应.图4~8给出了系统的动力学响应结果.
图3所示的扰动力矩所积累的角动量为零,但在卫星本体受到的扰动结束后,由于所激励的阻尼平台的运动和柔性梁的振动,姿态运动仍然会持续一段时间.随着阻尼平台平动和转动运动的衰减,星体姿态角速度逐渐稳定于零,且柔性梁的弹性振动也随之衰减.
为了进一步验证阻尼平台在衰减柔性附件振动方面的作用,现将阻尼平台从系统去除,柔性梁直接固支在星本体上,其它仿真条件与带有阻尼平台的情形一致,得到的仿真结果如下所示.由此组仿真结果可以看出,未加入阻尼平台时,在同样的外部激励下,星体角速度呈持续震荡趋势,柔性附件振动幅度远高于加入阻尼平台的情况.
对比两组仿真结果可以看出,阻尼器的引入可有效地衰减柔性附件的振动,起到隔振效果,同时能够有效抑制星体角速度的变化.显然,此类航天器尽管在结构和动力学上较中心刚体固接柔性附件的航天器要复杂,但在提高姿态控制响应速度和姿态控制精度方面则具有潜在的优势.
6 结 论
本文以带有柔性附件六自由度阻尼器的航天器系统为研究对象,利用多体建模理论中的Kane方程建模方法建立了系统的动力学方程.该方程具有较强的通用性,可用于系统控制器的设计.数值仿真结果表明,阻尼器能够有效衰减柔性附件的振动,有利于星体受扰后的快速稳定.
[1] BONG W. Classical and robustH∞control redesign for the hubble space telescope[J]. Journal of Guidance Control and Dynamics,16(6): 1069-1077, 1993.
[2] BONG W, BYUN K. New genralized structural filtering concept for active vibration control synthesis[J]. Journal of Guidance, Control and Dynamics, 1989, 12(2): 147-154.
[3] JEFFREY W U. SRTM mast damping subsystem design and failure investigation[C]//Proceedings of the 35thAerospace Mechanisms Symposium. New York: Ames Research Center, 2001.
[4] LEONARD M, MOON K. K. Dynamics and control of spacecraft with retargeting flexible antennas[J]. Journal of Guidance, Control and Dynamics, 1990, 13(2): 241-248.
[5] ANDREW J M, GARY L G, ANDRE P M. Nonlinear spacecraft dynamics with a flexible appendage, damping, and moving internal submasses[J]. Journal of Guidance, Control and Dynamics, 2001, 24(3): 605-615.
[6] 史纪鑫, 曲广吉. 可变构型复合柔性结构航天器动力学建模研究[J]. 宇航学报, 2007, 28(1): 130-135. SHI J X, QU G J. Mathematical modeling of a class of variable structure spacecraft with flexible multibody appendages[J]. Journal of Astronautics, 2007, 28(1): 130-135.
[7] 贾英宏, 徐世杰, 聂润兔. 充液挠性航天器的建模与动力学分析[J]. 北京航空航天大学学报, 2003, 29(1): 35-38. JIA Y H, XU S J, NIE R T. Modeling and dynamics analysis of liquid-filled flexible spacecraft[J]. Journal of Beijing University of Aeronautics and Astronautics, 2003, 29(1): 35-38.
[8] 黄文虎, 邵成勋. 多柔体系统动力学[M]. 北京: 科学出版社, 1996.
Dynamic Modeling of Flexible Multi-Body Spacecraft withDamping Mechanism
ZHU Mengping, GENG Lei, CHEN Xinlong, LI Zhi
(QianXuesenLaboratoryofSpaceTechnology,ChinaAcademyofSpaceTechnology,Beijing100094,China)
The dynamics of spacecraft with root damper of antenna mast is investigated. The system consists of a spacecraft main-body, several six-freedom rigid damper platforms and flexible appendages which are connected with the damper platforms. The damper platforms are connected with the main-body by elasticity-damp mechanisms. Hybrid coordinates are used to describe the system motion. System dynamics which are established via using Kane’s equations have better versatility and are advantageous to controller design. Numerical simulation results show that the damper can efficiently attenuate elastic vibration of the appendages, which is beneficial for spacecraft rapid stabilization after disturbance.
flexible appendage; damper; dynamics; Kane’s equation
2016-08-24
朱孟萍(1983—),女,工程师,研究方向为航天器姿态动力学与控制;耿 磊(1985—),男,工程师,研究方向为飞行器控制;陈新龙(1976—),男,高级工程师,研究方向为飞行器总体设计;李 志(1966—),男,研究员,研究方向为飞行器设计.
V448.22
A
1674-1579(2017)03-0034-07
10.3969/j.issn.1674-1579.2017.03.006
