多约束条件下月球南极探测返回窗口设计

冯 飞，张雅声

(1. 装备学院研究生院，北京 101416； 2.装备学院航天装备系，北京 101416)



多约束条件下月球南极探测返回窗口设计

冯 飞1，张雅声2

(1. 装备学院研究生院，北京 101416； 2.装备学院航天装备系，北京 101416)

针对月球南极探测任务，综合考虑中国地基深空测控系统现状、月球南极地区光照及地球再入终端等约束条件，利用月球反垂点概念，提出一种从环月轨道出发的三级返回窗口搜索策略.其次，提出一种改进多圆锥截线法，将月球非球形摄动加入到区间的轨道外推中，基于二级返回窗口对返回轨道进行了初步设计.给出以月球南极地区Shackleton撞击坑边缘一点为假定落点，于2020年自月球南极地区返回的仿真算例.仿真结果表明：一方面，窗口搜索方法可以有效解决多约束条件下的月球南极返回窗口设计问题；另一方面，改进多圆锥截线法作为一种初始轨道设计方法，可以有效减少再入误差，同时为后续高精度轨道积分提供良好初值. 关键词： 月球南极地区；月地返回轨道；返回窗口；反垂点；改进多圆锥截线法

0 引 言

近年来，随着技术的不断成熟及潜在的丰富科学价值，月球南极地区已成为各个国家或组织深空探测的重要目标之一[1]，欧空局、日本、俄罗斯都制定了详尽的月球南极采样返回任务规划[2-3].国内对奔月段轨道发射窗口的研究成果较为丰富[4-5]，但对月球南极返回轨道及其窗口的研究相对较少.郑爱武等[6]将月地转移轨道设计和再入角计算相结合，提出了一种返回窗口搜索策略；高玉东、白玉铸等[7-8]对月地转移轨道设计和相关特性进行了研究.同时，自月球南极地区的返回窗口还受到南极地区光照、通信等诸多因素的限制，呈现出新的特点.国外方面，Chuang等[9]对月球南极返回的策略进行了研究，但并无模型描述.Diego[10]结合ESA月球着陆任务，对南极地区的多个潜在着陆点的特性进行了分析.

文章综合考虑月球南极地理条件和地球再入终端约束条件，以中国地基深空测控网为依据，结合欧空局对南极地区的观测数据，提出了一种针对月球南极返回任务的三级返回窗口搜索策略，并通过改进多圆锥截线法计算初始转移轨道，对设计实例进行了仿真验证，为中国后期的探月任务规划提供技术参考.

1 返回窗口设计策略及转移轨道数学模型

1.1 约束条件分析

充足的光照及良好的测控条件是有人或无人月面探测任务的前提.月球南极返回任务的特点在于南极地区太阳高度角极小，太阳直射点近似在月球南北纬(-1°32′32″,1°32′32″)范围内周期运动，且部分地区在部分时间内的光照度呈现出很大差别，同时测控条件也较为苛刻，这就对月面探测任务提出了较为严格的时间约束条件.

另一方面，再入终端对返回窗口的约束最为严格，包括返回落区位置的约束、回收条件的约束、再入点位置及再入角的约束等.这里引入反垂点[11]的概念，反垂点是指轨道射入(transearth injection，TEI)时刻月地连线在地球背离月球一侧与转移轨道的交点，一般在近似分析中认为，月地连线总是在背离月球一侧与返回轨道相交的[12].易知，反垂点的赤纬与TEI时刻月球赤纬大小相等，符号相反.

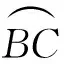
由球面三角形正弦公式得

(1)

(2)

(3)

文献[12]中证明，将转移轨道地心段近似为抛物线时，可得再入点θA至近地点的角距为再入角绝对值的2倍，在图1中即为

β+ω2=2|θA|

(4)

再入点A至着陆点的角距α可表示为

α=β+ω1

(5)

以上各关系式的意义在于理清了再入点纬度与着陆场纬度之间的关系，在近似分析中可以将近地点与月球反垂点视为重合，以便于通过改变返回窗口来调整月球反垂点的位置，进而确定合适的再入点纬度.

1.2 返回窗口设计策略

本文提出的设计策略是：首先根据任务规划确定发射年窗口；其次按照约束条件的强弱顺序，进一步确定满足月球南极光照、测控条件约束的返回窗口，称为一级窗口；之后在此窗口内利用二体拼接模型搜索符合地球再入终端约束的次级返回窗口(也称二级窗口)，最终在改进多圆锥截线法轨道计算中搜索确定符合全部约束条件的返回窗口(三级窗口).其中，年窗口设定为2020年，图2为具体设计过程流程图.

1.3 返回轨道动力学模型

多圆锥截线法是一种介于双二体拼接与高精度轨道积分之间解决多体问题的半数值解法.相比于双二体拼接法，它不是单纯的忽略多体引力，而是把转移时间分成若干小区间，在区间内以二体传播为主，并加以多体引力修正.文献[13]在月地转移轨道设计中，除三体引力外，考虑了地球引力位的J2项摄动，但在月球段轨道外推时仅将月球等效为球形引力体.事实上，地球非球形摄动在月地返回过程中的影响是非常有限的.以周期为3.5天的典型月地转移轨道为例，近月点轨道高度181 km，表1列出了不同摄动力对地球再入终端位置偏差的影响.

摄动力地球再入端位置偏差/km太阳引力(质点)2059.55月球非球形(21阶)407.92太阳辐射压12.46地球非球形J25.39

由于月球非球形摄动力作用在转移轨道初段所造成的偏差会在整个转移轨道中不断积累并发散，这与地月转移轨道中的情况有着很大差别.本文提出一种改进多圆锥截线法，将月球非球形摄动加入到月球影响球范围内的区间外推中，有效提高再入终端精度.

图3描述了多圆锥截线法的计算流程，详细推导过程见文献[14]，本文不再赘述.其中需要额外注意的是，在以月球为中心引力体的月心坐标系中，除地球对探测器的直接引力以外，地球和太阳产生的摄动加速度之和可表示为

(6)

式中：REM、rCM、RSM为探测器分别在地球、月球、太阳惯性坐标系中的位置矢量，μE、μS为地球、太阳的引力常数.因多圆锥截线法中涉及“状态回溯”及考虑地球中心引力的“状态外推”等设计步骤，故式(6)没有重复考虑地球对探测器的直接引力.

探测器在返回全程受力环境变化明显，采取以下变步长策略设置预报步长可提高计算效率

(7)

式中，S0为用户输入的步长因子.目的是通过设置合适的步长因子，使探测器在近月段和近地段力学环境变化剧烈处采用小步长，反之采用较大步长.图4 显示了当S0=0.01时，迭代步长的变化.

2 仿真结果与分析

2.1 光照与测控约束仿真分析

在2020年，太阳直射月球南半球的时间出现在这一年中的1月至次年6月.本文以月球南极附近的Shackleton撞击坑的边缘一点(89.778 8°S，153.434 9°W)为例，分析2020年1月至2020年6月期间其光照情况，如表2所示.

表2 2020.01—2020.06 Shackleton撞击坑边缘光照分析Tab.2 Lighting results of Shackleton rim from 2020.01 to 2020.06

可见，这一地区最长持续光照区间出现在2020-01-12 T 22:59—2020-06-02 T 17:47，对这一区间内当地的太阳高度角计算后得图5.考虑到当地地势地貌的情况，选取太阳高度角在1°以上的有效区间为2020-02-11 T 14:14―2020-05-02 T 16:11.

将位于智利的Santiago站、位于黑龙江的佳木斯站和位于新疆的喀什站组网，设雷达最小仰角为5°，可计算得到3个测控站组网后在2020年对南极Shackleton地区每个月的可见天数，如图6所示.在上文确定的有效光照区间内，测控站对该地区的可见情况如图7所示.

由于白道面与地球赤道面夹角的存在以及纬度天平动现象，在有效光照区间内，存在四段可被测控的区间，并以月球公转一周为单位呈规律性分布，且每段区间上都存在部分测控断点(盲区).此外，Santiago测控站的可见区间相对更长，这是因为此时月球的地面投影位于地球南半球，使得同样处于地球南半球的Santiago测控站受地球与月球遮挡影响相对较小.

结合上文对南极地区光照情况的分析，这样就确定了4段同时满足光照和测控约束条件的返回窗口，记为一级返回窗口，如表3所示.

表3 一级返回窗口Tab.3 First-stage window

2.2 再入终端约束仿真与分析

图8将表3中的4个一级返回窗口分别在白道上对应的月球位置进行了拟合，忽略了白道面空间指向的微小变化.可以看出：大部分返回窗口对应的月球位置都出现在白道、赤道交线以上的区域中，即星下点位于地球北半球的时刻，此时月球南极区域不受遮挡.但该区域内月球反垂点位于地球南半球，不符合再入要求.结合任务时长，月球应位于白、赤平面交线处附近，同时太阳与月球位置分别位于地球的两侧，符合回收光照要求.可见，满足此要求的返回时间只集中在第二、第三个一级返回窗口中.弹道-升力式再入方式所对应的月球反垂点纬度上限设定在北纬7°，即对应于月球星下点南纬7°.此时在第二、第三个一级返回窗口中对应的时刻分别为2020-3-12 T 21:23与2020-4-9 T 08:28，以上可在一级返回窗口的基础上确定同时满足再入要求的二级返回窗口，如表4所示.

窗口(UTCG)持续时间/h2020-03-09T20:07—2020-03-12T21:2373.32020-04-05T17:58—2020-04-09T08:2881.5

2.3 轨道动力学模型仿真与分析

基于文献[11]的双二体拼接的轨道模型，对表4 的二级返回窗口进行遍历，分别在第一、第二个二级返回窗口中得到了12组满足再入条件的轨道根数，而在第二个返回窗口中计算出轨道的再入时刻早于第一个时间窗口中的结果，因此从回收条件考虑，应尽量选择第二个返回窗口.在此窗口内利用改进多圆锥截线法，同时综合考虑能量最省的约束，得到在地球J2000惯性坐标系中的返回轨道历元及轨道根数如表5所示，仿真结果如图9所示，其中标记为蓝色的部分表示月球影响球内的转移轨道，红色表示地球影响球内的转移轨道.其中，为保证在一定计算精度的前提下提高计算效率，设定探测器在月球影响球内时为月球非球形引力场，出月球影响球后按月球球形引力场传播，同时考虑地球引力场J2项摄动.

设月球影响球半径为66 200 km，图10为探测器分别在传统多圆锥截线法与改进方法中运动至月球影响球边界时的位置、速度传播情况，其中月球非球形引力取前三阶.不难发现，月球非球形引力对探测器位置和速度矢量的影响主要集中在X和Vx方向，考虑非球形摄动后位置和速度的绝对值增加.而Y、Z方向上的影响相对较小，在邻近月球影响球出口处才呈现出发散趋势.需要声明的是，位置与速度的传播情况与初值在很大程度上相关，工程中应结合具体任务具体分析.

表5 三级返回窗口及初值轨道的3个特征点状态Tab.5 Orbit epochs and states of three feature points

3 结 论

本文以月球南极地区探测任务为背景，给出了一种在光照、通信、地球再入终端等多约束条件下的返回窗口设计方法.同时，提出了一种改进的多圆锥截线法，并结合此方法，对2020年落点在Shackleton撞击坑边缘的月球南极返回窗口进行了设计，最终确定的返回时间为2020-04-08 T 09:37，并计算了月地转移轨道射入点、月球影响球出口点以及地球再入点的状态.仿真表明该计算方法的有效性，以及改进后的多圆锥截线法可以有效减小终端误差.需要声明的是，返回窗口的计算不可独立开来，应将发射窗口、任务周期以及实际工程中的多种约束结合综合考虑.后续工作可结合具体的任务需求，围绕月球南极的精确落点选取、通信中继等问题开展进一步研究.

[1] 冯飞, 张雅声. 月球探测的新趋势以及对“嫦娥”工程的启示[C]//第一届中国航天指挥与控制论坛论文集.北京：中国指挥与控制学会,2014,80-85. FENG F, ZHANG Y S. The new development tendency of lunar exploration and enlightenments to the Chang’ e program[C]//Proceedings of the 1stChinese Forum of Command and Control. Beijing: Chinese Institute of Command and Control,2014,80-85.

[2] CARPENTER J D, FISACKERLY R, DE ROSA D, et al. Scientific preparations for lunar exploration with the european lunar lander[J]. Planetary and Space Science, 2012, 74(1): 208-223.

[3] Russian Federal Space Agency. Russia space programs and exploration handbook [R]. Moscow: Russian Federal Space Agency, 2011: 59.

[4] 李立涛, 张振民. 奔月转移轨道的快速设计方法研究[J]. 航空学报, 2003, 24(2): 152-156. LI L T, ZHANG Z M. Study of rapid design method for cislunar transfer trajectory[J]. Acta Aeronautica et Astronautica Sinica, 2003, 24(2): 152-156.

[5] 曾国强, 任萱, 郗晓宁. 快速设计月球卫星转移轨道的一种代数法[J]. 国防科技大学学报, 2000, 22(2): 1-6. ZENG G Q, REN X, XI X N. An algebraic method for fast design of lunar satellite transfer trajectory[J]. Journal of National University of Defense Technology, 2000, 22(2): 1-6.

[6] 郑爱武, 周建平. 直接再入大气的月地返回窗口搜索策略[J]. 航空学报, 2014, 35(8): 2243-2250. ZHENG A W. ZHOU J P. A search strategy of back windows for Moon-to-Earth trajectories directly returning to the Earth[J]. Acta Aeronautica ET Astronautica Sinica, 2014, 35(8): 2243-2250.

[7] 高玉东.月球探测器地月空间转移轨道研究[D]. 长沙： 国防科学技术大学, 2008. GAO Y D. Study on the cislunar transfer trajectory of the lunar probe[D]. Changsha： National University of Defense Technology, 2008.

[8] 白玉铸.载人登月轨道设计相关问题研究[D]. 长沙： 国防科学技术大学, 2010. BAI Y Z. Research on trajectory design for manned lunar landing mission [D].Changsha： National University of Defense Technology, 2010.

[9] CHUNG M K J, WEINSTEIN S S. Trajectory design of lunar south pole-aitken basin sample return mission[C]//AIAA/AAS Astrodynamics Specialist Conference and Exhibit. Washington D.C.: AIAA, 2004: 1-10.

[10] DIEGO D R, BUSSEY B, CAHILL J T, et al. Characterisation of potential landing sites for the european space agency’s lunar lander project[J]. Planetary and Space Science, 2012, 74(1): 224-246.

[11] STANLEY D, COOK S, CONNOLLY J, et al. NASA’s exploration systems architecture study[R]. NASA Final Report, TM-2005-214062, 2005.

[12] 沈红新, 李海阳, 彭祺擘, 等. 探月飞行器定点返回轨迹特性分析[J]. 国防科技大学学报, 2011, 33(4): 6-11. SHEN H X, LI H Y, PENG Q B, et al. Point return trajectory characteristics analysis for a lunar spacecraft[J]. Journal of National University of Defense Technology, 2011, 33(4): 6-11.

[13] 沈红新. 载人登月定点返回轨道问题研究[D]. 长沙： 国防科学技术大学, 2009. SHEN H X. Research on returning orbit from the moon to a specified landing site for manned lunar-landing mission[D]. Changsha： National University of Defense Technology, 2009.

[14] BYRNES D V, HOOPER H L. Multiconic: a fast and accurate method of computing space flight trajectories[R]. Washington D.C.： AIAA, 1970.

Design of Launch Window for Lunar South Pole ReturnMission with Multi Restrictions

FENG Fei1， ZHANG Yasheng2

(1.DepartmentofGraduateManagement,EquipmentAcademy,Beijing101416,China;2.DepartmentofSpaceEquipment,EquipmentAcademy,Beijing101416,China)

Aiming at the mission of Lunar south pole exploration, a launch window searching method of three stages is proposed, taking illumination conditions, the status quo of Chinese ground based TT&C systems and the constraint conditions of Earth reentry process into consideration. A return trajectory is calculated by an improved multi-conic method, which combines the lunar oblateness correction in trajectories propagation. Furthermore, return trajectory simulations from Lunar south pole are carried out based on an assumed site in Shackleton rim in 2020. Results show that this launch window searching method is effective and accurate. Additionally, the improved multi-conic method can reduce the terminal boundary errors effectively.

lunar south pole region； Moon-Earth trajectory； launch window； lunar antipode; improved multi-conic method

2017-02-21

冯 飞(1990—)，男，博士研究生，研究方向为航天任务分析和设计；张雅声(1974—)，女，教授，研究方向为航天任务分析和设计.

V412.41

A

1674-1579(2017)03-0021-07

10.3969/j.issn.1674-1579.2017.03.004