安徽省制造业的生产效率及其收敛性研究
——基于超效率 DEA 模型以及 Malmquist指数的分析
2017-07-03余华银
朱 婉,余华银
(安徽财经大学 统计与应用数学学院,安徽 蚌埠 233030)
安徽省制造业的生产效率及其收敛性研究
——基于超效率 DEA 模型以及 Malmquist指数的分析
朱 婉,余华银
(安徽财经大学 统计与应用数学学院,安徽 蚌埠 233030)
基于超效率 DEA 模型构建了安徽省制造业的生产效率评价指标体系,利用 MaxDEA6.0 软件,对 2006-2014 年安徽省制造业的各项指标数据进行了 Malmquist 指数分析及其分解,评价技术效率指标和技术进步指标,最后对安徽省制造业生产效率的差异性及其收敛性进行探讨。 实证结果显示,横向上安徽省制造业中资源密集型、劳动密集型、技术密集型以及资本密集型之间的生产效率值存在差异,纵向上各行业都存在不同程度的波动,且制造业整体的差异水平高于这 4 大分类之间的差异,30 个制造业行业呈现“总体收敛,局部发散”的特点,生产效率低的行业具有向生产效率较高的行业追赶的倾向,所以可以认为安徽省的制造业总体是协调发展的。
制造业;超效率 DE;Malmquist指数;收敛性
1 前 言
工业改革是人类文明的一大进步,随着工业化的发展,各国逐步进入现代化生产。工业发展直接体现的是制造业的生产进步,现如今制造业的发展更是体现了一个国家的生产力水平,在国民经济中扮演重要角色。在我国制造业作为支柱产业,近几年的发展态势良好,每年制造业的增加值在 GDP 的组成中都占有重要地位。对一个国家而言是这样,对一个省而言亦是如此。 我国自 2004 年提出中部崛起计划以来,中部 6 省的经济发展水平出现了显著提高,安徽省作为中部崛起的典型省份,近几年的制造业发展势头强劲,据安徽省 2015 年国民经济和社会发展统计公报显示,2015 年的地区生产总值为 22005.6亿元,按可比价格计算,比上年增长 8.7%,其中制造业增长 9.3%。
但是在资源稀缺的今天,如果一味的追求量的增长,不注重投入产出之间的比率关系,则无论对于企业还是环境资源而言都没有达到帕累托最优。所以现在很多的经济学学者们都将“生产效率”作为自己的重点研究领域,探索如何使得企业通过投入最少的资源来达到资源的有限性和人们不断增长的物质文化需求的均衡状态。“生产效率”问题反映了投入转化为产出的水平,能很好地衡量一个行业的发展情况,近些年来很多学者运用了不同的评价方法来分析多个行业的效率,其中涉及制造业、医疗卫生、粮食生产、财政支出等,但是对于制造业的效率研究,主要还是集中在制造业的技术创新能力、技术创新效率、制造业转型等方面,并且关注点集中在高新技术产业上,对于制造业全局的生产效率的评价研究比较少。
另一方面虽然近几年国内学者对于制造业生产效率的研究越来越深入,但是这些研究大多是从省域之间比较的角度出发进行研究,对于具体某个省的制造业全局横向行业之间以及纵向动态比较较少。 因此,本文通过构建超效率 DEA 模型对 2006-2014 年安徽省的全部制造业行业技术生产效率以及技术进步效率进行评价,随后对效率值的差异性进行分析,根据差异性分析其收敛和绝对收敛,最后根据实证结果,从行业、政府等角度提出提高安徽省制造业协调发展效率的相关建议。
2 方法介绍
2.1 经典数据包络分析(DEA)
DEA 法又称数据包络分析法(Data Envelopment Analysis,DEA), 是由美国运 筹学大师 A Charne 和W.W.Cooper 于 1978 年 提 出 来 的 。 首 个 DEA 模型——CCR 模型。基本原理是利用线性规划模型,将几个具有相同的多投入与多产出类型的主体看作是不同的决策单 元 DMU(Decision Making Unit),将 最少的投入实现最多的产出视为生产前沿线,并通过比较 DMU 与有效生产前沿线的投入产出比, 对各DMU 的生产效率进行综合评价。CCR 模型是一种理想的模型,适用于 DMU 最优规模运行的情况,自CCR 模型提出以来,更多的模型也随之推陈出新,这些新模型的应用领域也更加宽泛。
CCR 模型最经典的DEA模型,具体构建方法如下。
假设有 n个 DMU, 每个 DMU 都有 m 种投入以及 S 种产出,则评价第 j决策单位的生产效率,以投入为导向的 CCR 模型为:
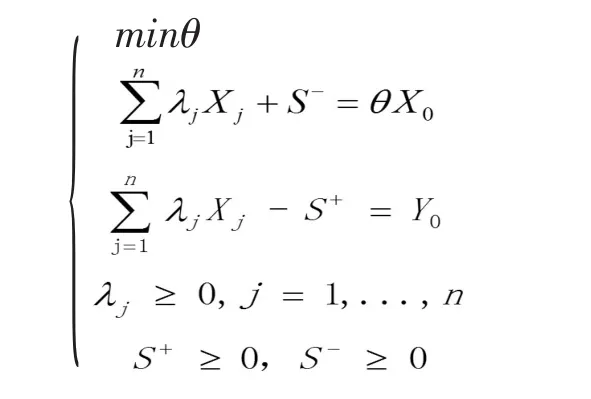
在 CCR 基本结构中,θ为决策单元 DMUj的有效值。 S+,S-为规划的松弛变量;λj有效 DMU 组合第 j个决策单元 DMUj的组合比例。 在该模型中:(1)当θ=1,并且 S+=S-=0 时,则称该 DMU 为 DEA 有效 ,即此时的投入产出的比例达到最优;(2)当 θ=1 且 S+≠0 或 S-≠0 时, 则称该 DMU 为 DEA 弱有效;(3)当θ<1 时,则称该 DMU 为 DEA 无效。
2.2 超效率 DEA 模型
当上述的 CCR 模型得到有较多个 DMU 实现了DEA 有效时,如果要继续对这些都实现了 DEA 有效的决策单元进行评价,则该模型就有了局限性。此时超效率 DEA 模型的提出就实现了有效决策单元之间 的 可比性 。 超 效率 DEA 方法 的 基本思 想 是[1]:在多个决策单元体系中,对某个决策单元进行评价时,可以将该决策单元排除在体系之外。即在评价 j决策单元时,可以将包含该决策单元的体系与不包含决策单元的体系分别进行构建模型比较评价结果。在保持相对有效性的前提下,DEA 有效的决策单元可以按比例增加投入,当这种投入增加的比例达到最大时,此比例值称为 DEA 超效率值。 超效率 DEA模型的基本形式如下:

2.3 Malmquist生产率指数
Malmquist指数最早可以追溯到 1953 年, 是由瑞 典 的 经 济 学 家 Sten Malmquist 提 出[2]。 Caves 等 人受 到 Malmquist 消 费 指 数 的 启 发 , 从 理 论 上 将Malmquist指数运用到生产率的分析中,并称这种分析 生 产 率 的 Malmquist 指 数 为 Malmquist 生 产 率 指数。 此后,随着 DEA 方法的提出,Fare 等人又从实证角度实现了 Malmquist生产率指数 ,至此,Malmquist生产率指数实现了从提出到理论化再到实证化。Malmquist效率指数是在技术条件不变的情况下,比较 s时期到 t时期的技术效率变化。 距离函数是Malmquist 效 率 指 数 的 理 论 前 提 , 所 以 在 进 行Malmquist效 率指 数比 较 时 , 首先 需要 构建 距离函数。 投入距离函数是生产点(q,x)向理想的最小投入点压缩的比例,表示如下:
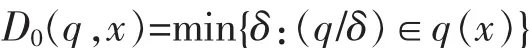
那么时期s下的距离函数可由如下的线性规划求 解[3]:
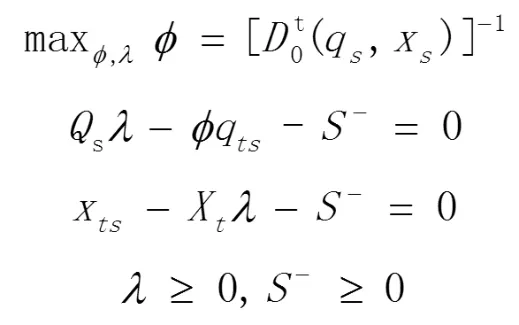
同时 Malmquist效率指 数可分解为技术效率指数和技术进步指数:
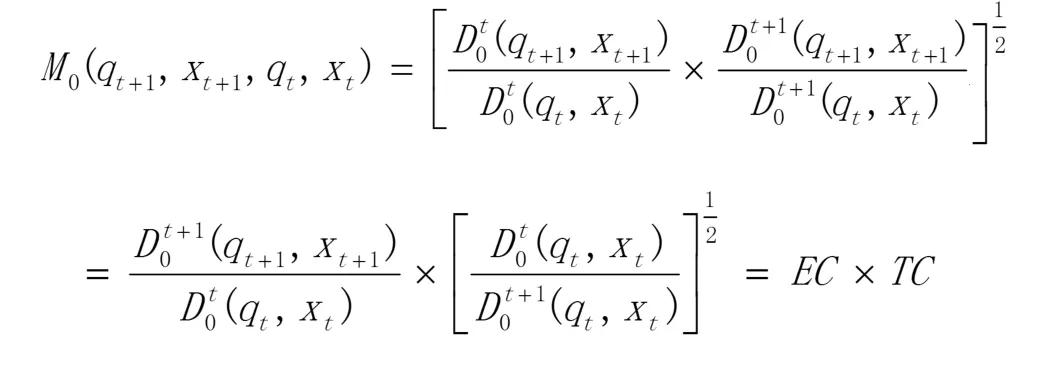
其中等式右边的第一部分记可以为技术效率指数(EC),第二部分记可以为技术进步指数(TC),所以对 Malmquist 效率指数进行分解还可以从 EC 和 TC这两个方面进行具体的分析比较。
2.4 效率的收敛性分析
在对制造业生产效率的收敛性进行分析时,可以分别对 σ收敛和绝对 β收敛分析。这两种收敛都反映了制造业之间的敛散程度,其中σ收敛可以用以下的统计量衡量:
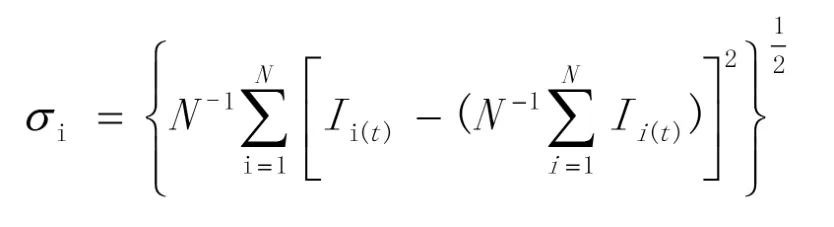
其中 Ii(t)表示第 i个决策单元 在 t时期的 DEA 效率评价值,N表示该体系中有多少个决策单元。
绝对β收敛是指效率水平较低的决策对象随着时间的推移,会向效率水平较高的对象趋同,这也就是说最终整个评价体系中的所有决策单元的效率值都会处于一个平衡状态。根据 Barro 等人关于经济增长是否收敛的研究方法, 这里绝对 β收敛是对前面计算出的效率值进行横截面分析,具体的回归系数用以下式子计算:
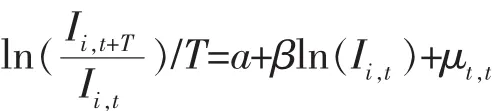
其 中 ,Ii,t和 Ii,t+T分 别 表 示 i第 个 决 策 单 元 , 在 t时期和 t+T 时期的 DEA 效率评价值,等式的整个左边表示该决策单元在T时期内的平均效率值增长率; 等式右边 的 a 为常 数项 ,β为 收 敛 系 数 ,μi,t为 随机扰动项。 若 β为负数,则存在绝对 β收敛;反之则不存在。因为本次的样本数据只有 2006-2014 年,为了最大效率地利用样本数据,并且使得数据具有连续性,本文将 T 取值为 1。
3 实证分析
3.1 评价指标体系的构建以及数据的来源
本次案例的数据均来自于安徽统计年鉴(2007-2015)与国民经济和社会发展统计公报,按照安徽统计年鉴的分类方法,将制造业分为农副食品加工业、食品制造业、酒饮料和精制茶制造业、烟草制品业、纺织业、纺织服装、服饰业、皮革毛皮羽毛及其制品和制鞋业、木材加工及木竹藤棕草制品业、家具制造业、造纸及纸制品业、印刷和记录媒介复制业、文教工美体育和娱乐用品制造业、石油加工、炼焦和核燃料加工业、化学原料和化学制品制造业、医药制造业、化学纤维制造业、橡胶和塑料制品业、非金属矿物制品业、黑色金属冶炼和压延加工业、有色金属冶炼和压延加工业、金属制品业、通用设备制造业、专用设备制造业、汽车制造业、铁路船舶航空航天和其他运输设备制造业、电气机械和器材制造业、计算机通信和其他电子设备制造业、仪器仪表制造业、其他制造业、废弃资源综合利用业 30 个行业,在本文中,为了方便叙述,分别以 1-30 的数字依次代表以上具体的制造业。
鉴于数据的可得性以及实际性,这里选取的产出指标有:
1.工业增加值(亿元):体现各制造业企业本期新增投入所创造的价值;
2.工业总产值(亿元):体现各制造业企业在本期内生产的产品总价值量;
3.工业销售产值(亿元):体现的各制造业企业本期生产并实现销售的产品总价值量,其中既有成品,也有半成品,也包括对外提供的工业性作业价值等;
4.主营业务收入(亿元):直接体现各制造业企业在本期内的主营业务收益情况。
投入指标有:
1.主营业务成本(亿元):直接体现本期内各制造业企业的主营业务投入的成本情况;
2.原煤用量(吨):体现本期内的原煤投入量;
3.用电量(亿千瓦时):电力资源是现代制造业生产不可缺少的投入,体现各制造业企业本期内的电能源投入量;
4.职工人数(人):体现各制造业企业本期内的人力资本投入量;
5.固定资产折旧(亿元):机器设备等的固定资产损耗是无形中的投入;
6.工业取水水总量(万立方米):体现水资源的投入使用量。如表1所示。

表1 评价指标体系
3.2 制造业的效率值水平分析
利用 MaxDEA6.0 软件,将 数据导入计算,得到的各行业各年份的效率值按照制造业的分类进行整理(这里的分类标准参照 Lall、盛斌等人对制造业的划分,即将制造业分为资源密集型、劳动密集型、技术密集型、资本密集型 4 类),并对制造业进行分类比较。
3.2.1 资源密集型制造业的效率值动态分析
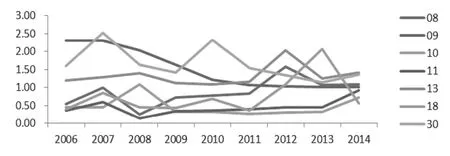
图1 资源密集型的效率值分布
从表1及折线图可以看出,资源密集型的制造业这几年的投入产出效率值总体差异比较大,但是波动较小。其中 10、11、18 三个行业的总体效率值偏低,13 行业 2006-2014 年的生产效率值比较稳定,且基本在均值1附近小范围波动,说明其大体是DEA 有效的,9 和 30 的效率值总体呈现波动平稳从高于1向等于1收敛,可以预见将来几年该行业的生产效率为 DEA 有效的。另从资源密集型行业的总体而言,所有的行业 DEA 效率值都呈现一种从大幅度大于1或者大幅度小于1的状态向效率值1慢慢趋近收敛的趋势,所以可看出这些行业近几年的生产效率一直在改进,且是有效性的改善。所以要保持近几年的技术工艺以及管理办法,最终实现 DEA有效。
3.2.2 劳动密集型制造业的效率值动态分析

图2 劳动密集型的效率值分布
总体上劳动密集型制造业的生产投入 DEA 效率值的差异以及差异的波动幅度都要显著于资源密集型产业,联系实际可得这些特点是由这类行业的生产特征决定的。这类行业的劳动力是主要的生产投入要素,所以当年的劳动者供求平衡状况以及就业率的大小对这些行业的生产效率有很大的影响。从图 2 可以看出 6、20、21 三者的 DEA 效率值较稳定,基本在 DEA 有效附近上下小幅度波动,所以可以看出这几个行业的 DEA 已经达到了有效,所以只需要维持现有的生产投入比例以及生产工艺,就可以始终保持生产 DEA 有效。 而对于 3、4、17 等的行业,DEA 效率值不稳定并且偏离 DEA 有效值幅度比较大,所以这些行业应该要加强现有的生产工艺,不仅要从技术效率改进,也可以从规模效率方面入手,多方面寻找造成 DEA 无效的原因。
3.2.3 技术密集型制造业的效率值动态分析

图3 技术密集型的效率值分布
相比较前两类,技术密集型行业的生产效率差异更大,不稳定性的造成原因可能是技术密集型的行业之间的所需要的支撑技术不同,虽说都需用复杂先进而又尖端的科学技术才能进行生产,但是具体的行业之间还是有差别,某一个或是几个行业的主要支撑技术得到了创新,可以减少投入但是保证产出不减少,那 DEA 有效性则更强,那该行业的生产效率则更接近于 1,变动比较明显,但是这种技术的改进对于其他技术密集型行业来说可能并没有很大的影响,则相对于技术改进的行业来说,DEA 效率值则会稳定些。所以两种行业的 DEA 变动幅度和范围会出现不同。
3.2.4 资本密集型制造业的效率值动态分析

图4 资本密集型的制造业效率值
资本密集型行业的生产效率总体波动幅度不大,稳定性要优于技术密集型行业。 其中 26 行业的DEA 生产效率在初期还是接近于 DEA 有效的,但是随着时间的推移,偏离程度持续走高。说明该行业的管理以及技术运用都需要改善。 12、24 行业的 DEA效率值是资本密集型行业中生产效率较为稳定的,25 行业这几年间几次穿越 DEA 有效值点,所以这些行业都需要整理近几年的数据经验,总结关键性的技术要素以及管理要素,确定最佳生产要素投入比。
3.3 Malmquist指数分析
MaxDEA6.0 软件直接给出了 ML 指数,以及 EC指数,TC 指数,对 30 个制造业行业 2006-2014 年的ML指数几何平均值,以如图 5的折线图的形式给出, 则可以看出从 2006-2014 年除了 29 突出大于1, 达到极值点 2.29, 其余所有的制造业行业的 ML指数都在 1 附近波动,且从总体的排名来看,技术密集型的行业排名普遍比较靠前,所以可以认为技术密集性的行业生产效率增加的速度高于其余的行业。联系实际技术密集型的行业主要是电子计算机工业,原子能工业,大规模和超大规模集成电路工业等,这些行业的生产动力主要依据技术创新,随着当代科学技术的进步,新科技的产生,新技术的投入,必然会引起这些行业的生产效率的快速进步。

图5 ML指数平均值
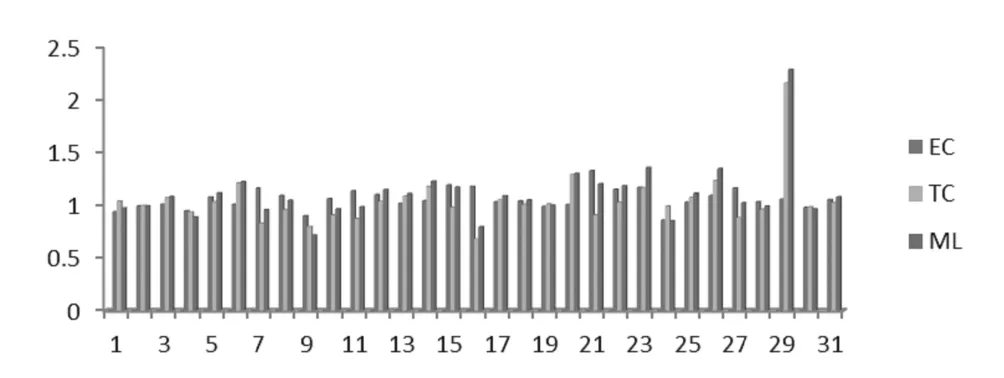
图6 ML 指数以及 EC、TC 分解
图6 显示,29 其他制造业的高 ML 值主要是由于高 TC(技术进步指数)引起的,ML 值 2.2843,其中 TC值为 2.1584,EC(技术效率指数)为 1.0583,这说明其他制造业的生产受到技术进步的影响很大,同样特点的还有 1、3、6、20、24、26 等行业,这可能是由于各自本行业的生产效率受到整体社会技术进步的影响要大于各行业对已投入的技术进行改进的影响,所以对于这些行业的效率进行改进时,要紧随时代的步伐,随时关注新技术的开发与投入使用。相反,对 7、8、9、10、11、16、21、27 等行业,以 16 为例,此行业的 ML 值为 0.7967, 其 中 EC 指 数 值 为 1.1722,TC 指 数 值 为0.6797,这些行业的生产受到对已投入的技术进行改进的影响大于整体技术进步的影响,所以对这些行业的改进要抓住已投入使用的生产技术同时,要根据现有的生产特点进行有目的的改进。
3.4 差异的收敛性分析
3.4.1 变异系数分析
还是将 30 个制造业行业分为资源密集型、劳动密集型、技术密集型、资本密集型4类进行比较分析。为了对不同行业以及不同类型分类的决策单元之间的差异性作出精确并且有效的比较和测量,使安徽省制造业的资源投入以及产出达到更好地帕累托最优,本文将通过计算各个行业生产效率的变异系数来衡量以及定量比较。
表2显示的是所有行业以及各分类的变异系数,30 个行业间的变异系数均值为 0.81, 而 4 大分类 之 间 的 变 异 系 数 分 别 为 0.62、0.72、0.55、0.49,所以能够看出所有行业间的差异性要明显于4大分类之间的差异程度。具体的4大分类之间的差异程度也不一样,其中劳动密集型的行业间生产效率差异要大于其余几个分类间的变异程度。而资本密集型的变异普遍要小于其他的分类。 结合图 5,可以看到所有行业间以及4大分类之间的变异系数动态变化特点。资本密集型的变异系数不仅是在绝对值上普遍处于最小的状态,而且整个的波动也最为平缓,资源密集型和劳动密集型行业具有忽高忽低的变动特点,变异系数极不稳定。这与改行业的生产特点息息相关,这些行业受到资源以及劳动力的影响程度比较大,而这些影响因素受到政策影响比较大,可以说对政策比较敏感,如果当年的资源供给或者劳动力的供给变动比较大,则变动自然也会比较剧烈。
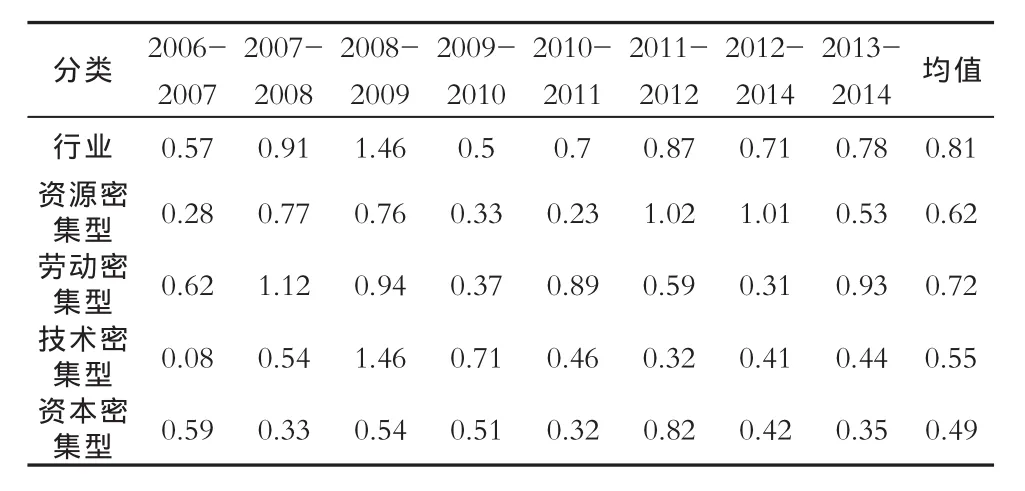
表2 变异系数统计表
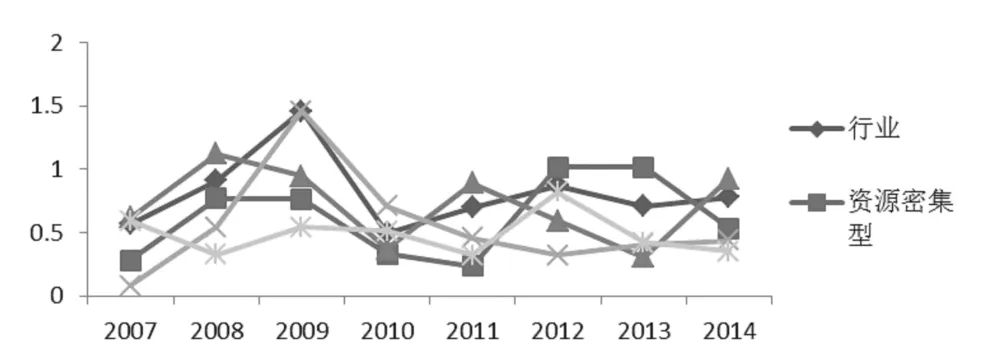
图7 变异系数变动情况
3.4.2 σ 收敛分析和绝对 β 收敛分析
根据 σ 的计算公式,将 30个行业间的 σ 值以及 4大分类的 σ 值的计算结果整理成如下表 3。从表中的数据可以看出安徽省 30个制造业行业间的整体呈现“总体收敛,局部发散”的特点,整个制造业的 σ 收敛值从 2007 年的 1.03 降到 2014 年的 0.73,这说明 30个行业间的生产效率的绝对差异是在逐步缩小的,总体呈现出 σ 收敛趋势。但是结合每年的动态趋势,2009 年达到最大值 2.29,紧接着 2010 年达到最低值 0.52,波动幅度比较大。 4 大行业分类中除了技术密集型,其他3类之间的绝对差异也表现出波动变化,但是最终总体是σ收敛的趋势。
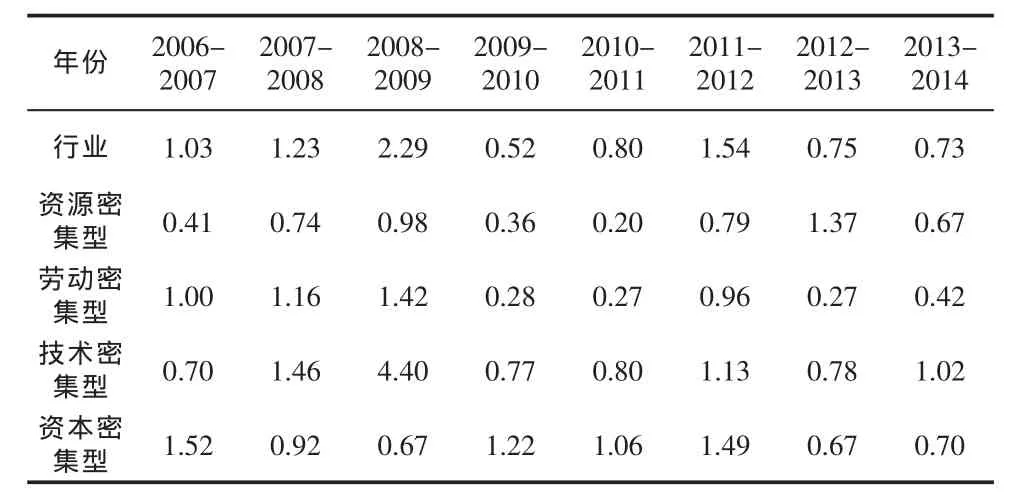
表3 生产效率σ值统计表
为进行绝对β收敛分析,先对面板数据进行平稳性检验,检验结果显示 P 值都小于 0.05,所以认为 5%显著性水平下,认为数据是平稳的,可以进行回归。
表4给出了生产效率绝对 β收敛的回归结果。从安徽省 30 个行业间来看,β 系数为-0.56,t统计值为-10.929,在 5%的置信水平再通过检验,所以可以认为本期的生产效率值对本期的生产效率增加率产生负向影响,所以安徽省制造业总体上呈现出绝对β收敛,并且各行业的生产效率会趋近于一个比较稳定状态,这与之前的 σ 收敛分析结论一致。从 4 大分类行业的角度来看,除了技术密集型产业,剩下的3个分类行业的回归系数在 5%的显著性水平下都通过了检验,可以认为 β 系数显著不为 0,所以是绝对β收敛的,这表明这些行业的生产效率之间存在着趋同的趋势,也就是说生产效率低的行业具有向生产效率较高的行业追赶的趋势。
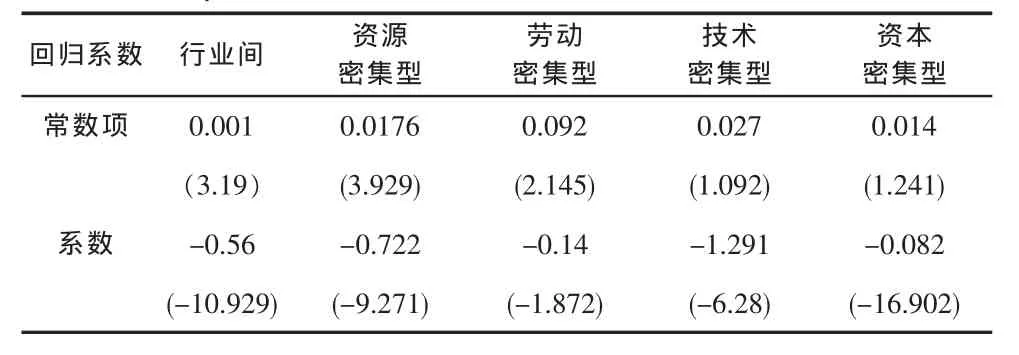
表4 绝对β收敛回归结果
4 结论以及建议
本文以安徽省统计年鉴上分类的 30个制造业行业的各项投入产出指标面板数据,利用超效率DEA 模 型 以 及 Malmquist 生 产 率 指 数 及 其 分 解 法 ,实证分析了 2006-2014 年的安徽省制造业的生产效率及其差异性,得到的主要结论如下。
1.样本期间内,安徽省制造业全要素生产率几何平均增长率为 8.02%, 其中技术效率以及技术进步效率的贡献相差不大。这说明总体而言,安徽省的制造业生产效率在高速前进的同时,能够兼顾技术效率和技术进步,目前还处于高速发展阶段。
2.样本期间内资源密集型、劳动密集型、技术密集型、资本密集型4大类制造业的动态生产效率具有不同的特点。其中资源密集型的生产效率总体是呈现发散型逐渐收敛于 DEA 有效的状态,劳动密集型总体是大多数行业分布于 DEA 有效附近,并伴有微小波动,技术密集型以及资本密集型的生产效率波动幅度大于前两者,不仅各行业自己的生产效率波动幅度很大,而且不同行业之间的生产效率值相差也很大。
3.Malmquist效率指数分析显示, 不同行业之间的 ML指数构成不一样,有些行业的高 ML值主要是由于高 TC(技术进步指数)引起的,比如农副食品加工业、酒、饮料和精制茶等行业,有些高 ML 值行业主要是由高 EC(技术效率指数)引起的,比如皮革毛皮羽毛(绒)及其制品业、木材加工及木竹藤棕草制品业、家具制造业等行业。所以不同行业对生产效率进行改进时要根据自己的特点,有效率的、有目的的实施措施。
4.收敛性分析显示安徽省的制造业生产效率呈现“总体收敛,局部发散”的特点。 这说明 30 个行业间的生产效率的绝对差异是在逐步缩小的,总体呈现出 σ 收敛趋势。但是结合每年的动态趋势,局部具有不稳定性,波动幅度比较大。4大行业分类中除了技术密集型,其他3类之间的绝对差异也表现出波动变化,但是最终总体是σ 收敛的趋势。
5. 安徽省制造业总体上呈现出绝对 β收敛,并且各行业的生产效率会趋近于一个比较稳定状态。并且各行业的生产效率之间存在着趋同的趋势,也就是说生产效率低的行业具有向生产效率较高的行业追赶的趋势。
根据以上的结论,结合安徽省的制造业生产环境,提出以下几点建议。
1.各具体制造业行业来说,各企业要认清自己的行业生产特点,技术投入以及资源投入的比例要结合行业的技术效率指数以及技术进步指数,制定的管理政策要与企业的生产相得益彰,而不是盲目跟风,这样可能会导致生产效率不升反降,甚至会失去自己原本的特色。
2.对于政府而言,在制定政策以及实施贯彻政策过程中,特别要注意对政府政策比较敏感的行业,比如劳动密集型行业和资源密集型行业。另外要高度重视新技术的研发,积极引进先进技术,将资源的配置结构做到最优,促进技术进步的同时提高技术效率,双轨驱动推进安徽省制造业的效率增长。
3.不管是技术效率还是技术进步,对于生产效率而言,都是最重要的增长因素,所以对于中央政府而言,应该高度重视科技创新,加快科技体制机制改革创新。要积极引导人力资源以及自然资源的分配,促进创新资源高效配置,完善对具有专业技能的人员激励措施。
4. 目前安徽省的制造业总体呈现绝对收敛,所以低效率的企业正在积极向高效率的企业靠近,总体呈现协调发展的状态。 DEA 生产有效的企业要保持自己生产优势的同时,尽量减少生产效率的波动性,低效率的企业要总结自己的生产经验,不断分析不足,向高效率企业推进。
[1]段婕,刘勇,王艳红.基于 DEA 改进模型的 装备制 造 业 技术创新效率实证研究[J].科技进步与对策,2012,(6):65-69.
[2]赵萌.中国制造业生产效率评价:基于并联决策单元的动态DEA 方法[J].系统工程理论与实践 ,2012(6):1251-1260.
[3] 夏 维 力, 钟 培 . 基 于 DEA-Malmquist 指 数 的 我 国 制 造 业R&D 动 态 效 率 研 究 [J].研 究 与 发 展 管 理 ,2011,23 (2): 58-66.
[4]柳顺,杜树新.基于数据包络分析的 模糊综合评 价方法[J].模糊系统与数学,2010,24(02):93-98.
[5]穆 文 杨.基 于 DEA 的 我 国 制 造 业 技 术 创 新 绩 效 评 价 [D].北京:北京交通大学,2010:34-35.
[6]吴超,邱家学.基于数据包络分析的我国医药制造业相对效率分析[J].中国新药杂志,2013,22(23):2730-2734.
[7]童晶晶.基于 DEA 的我国创业板制造业上市公司绩效评价研究[D].合肥:合肥工业大学,2012:23-38.
[8]罗 艳.基 于 DEA 方 法 的 指 标 选 取 和 环 境 效 率 评 价 研 究[D].合肥:中国科学技术大学,2012:32-36.
[9]吴 德 胜.数 据 包 络 分 析 若 干 理 论 和 方 法 研 究[D].合 肥 :中 国科学技术大学,2006:22-34.
责任编辑:胡德明
The Production Efficiency and Convergence of the Manufacturing Industry in Anhui Province——An Analysis Based on Super-efficient DEA Model and Malmquist Index
Zhu Wan,Yu Huayin
(Institute of Statistics and Applied Mathematics,Anhui University of Finance and Economics,Bengbu 233030,China)
This article first establishes a production efficiency evaluation index system for the manufacturing industry in Anhui based on the super-efficient DEA model,and then selects the manufacturing data from 2006 to 2014 in Anhui province to make a Malmquist index analysis and decomposition and evaluate technique efficiency and technical progress index by using MaxDEA6.0.And finally,the difference in production efficiency and astringency of manufacturing industries in Anhui are discussed.The empirical results show that horizontally differences in production efficiency exist among resource-intensive manufacturing,labor-intensive manufacturing,technology-intensive manufacturing and capital-intensive manufacturing in Anhui province,and vertically different degrees of fluctuation exist in every industry.What's more,the overall difference of the manufacturing industry is higher than the difference among the four categories.30 manufacturing industries are characterized by"overall convergence,local divergence".Industries with low production efficiency tend to chase those with higher production efficiency,so in Anhui province the manufacturing industries have achieved coordinated development in general.
manufacturing;super-efficient DEA;Malmquist index;astringency
F424
:A
:1672-447X(2017)03-0007-07
2017-03-13
朱婉(1992-),安徽黄山人,安徽财经大学统计与应用数学学院硕士研究生,研究方向为宏观经济统计分析;
余华银(1962-),安徽全椒人,安徽财经大学统计与应用数学学院教授,名誉院长,研究方向为宏观经济统计分析。
