基于复合多层 RBF网络的组合预测的研究
——以商业银行农村信贷为例
2017-07-03盛国敏
盛国敏,庄 健
(1.中国农业银行 天长市支行,安徽 天长 239300;2.安徽工业大学 商学院,安徽 马鞍山 243000)
基于复合多层 RBF网络的组合预测的研究
——以商业银行农村信贷为例
盛国敏1,庄 健2
(1.中国农业银行 天长市支行,安徽 天长 239300;2.安徽工业大学 商学院,安徽 马鞍山 243000)
为了解决多元线性回归和 logistic 回归在预测中的精度不高问题,运用组合预测的思想,提出通过开发运用复合多层 RBF 神经网络将多元线性回归和 logistic 回归组合的预测方法,并应用于商业银行的个人信用评估中,其结果表明组合预测方法能够获得比单层 RBF 网络法和单一回归方法更高的预测精度。
多元线性回归;logistic 回归;复合多层 RBF 神经网络;组合预测;个人信用评估
信用伴随人们一生,是一生积累的信任度和诚信度的体现。在商品交换等经济活动中,它是一种价值的运动,是整个市场经济发展的基石。 在我国,信用已经是人们立信他人的基础,是社会经济活动的“身份证”。 我国信用基础建设发展缓慢,尤其是个人信用额度预测体系建设很不完善,失信违约事件时常发生已成为当前市场经济发展的基本特征,阻碍着我国消费经济的快速发展。
在 很 多 发 达 国 家 中 ,个 人 信 用 评 估 方 法[1]已 经 发展到成熟地步。除各种统计方法外,人工智能技术如神经网络、专家系统、分类树以及遗传算法也得到了广泛的重视。虽然现在已经有很多高新技术工具和各类软件在商业经济中加以使用,但是由于我国个人信用体系建设的较晚,已有的信用评价机制发展相对落后,在评估方法的精确度方面不尽人意。因此本文试图通过构建新的复合多层 RBF 神经网络来评估个人信用,为解决上述问题进行的尝试。
径 向 基 函 数 网 络[2]是 一 种 性 能 优 良 的 前 馈 型 网络,具有不存在局部最优解和学习速度快的优点,因此被广泛应用到各个领域。径向基函数网络自提出以后,发展了许多算法,这些算法大都旨在改进中心的选取,宽度系数的确定,径向基函数个数的确定方法 和减少 计 算量,具 体 见文献[3-8]。
1 模型构建原理
个人信用评估可以被看作是模型识别中的异类分类问题——通过历史上不同类别的 (信用好和信用不好)的若干样本,从调研的样本中提取、分析其规律,建立数学模型,然后用于新样本的判断。 直观地说,就是将个人信用的评估转化为各种指标体系的量化问题——贷款申请者最后能否还本付息取决于其个人基本的经济和信用状况。目前个人信用评价机制主要有多元判别分析法等数学模型方法和神经网络法等人工智能方法。
从总体上说,这些模型均可以统一为分类问题,就是按照历史数据建立判别模式,将新的需要分类的样本数据代入,得到一个输出值,从而确定样本的分类。这些方法可以说是信用评估过程中的主流方法,得到了广泛的应用,但应该说不同的方法都存在一定的问题,如多元判别分析模型是根据特定样本数据建立的,一个地方建立的模型不一定适合其他地方,还要求样本满足正态分布、协方差等过于严格的前提条件,并且模型有用性比较差。 而 RBF 神经网络也存在隐层神经元个数难以确定,各层核函数的中心不能很好分配在恰当的位置上等问题。从信息论的角度来看,每一种预测方法都包含其特殊的信息,即便是相对比较差的预测方法,也一定会包含着其他的方法所不具有的独特信息。因此,为了尽可能多的利用全部有效信息,可以采用一定的方法和手段对不同的方法进行组合,这就是所谓的组合预测[9]。
这里选取个人信用评估过程中应用比较成熟、效果比较明显的线性回归和 logistic 回归方法,通过基于复合多层 RBF 神经网络构建的组合预测模型,希望将复合多层 RBF 神经网络的高精度和线性回归、logistic 回归方法的高稳健性有效结合,并克服各自的缺点。
1.1 多层 RBF 网络中的聚类算法
构建第一层的输出网络。程序中输入样本X为
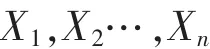
和它们所对应的期望输出值是
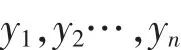
做增广样本为
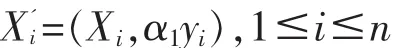
这里 α1>0。 再用 K-mean 法将

分成 m1个聚类
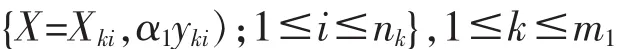
这样得到 m1个样本聚类
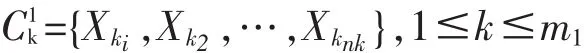
把每个聚类的均值作为聚类中心,即


于是网络第一层表达式为
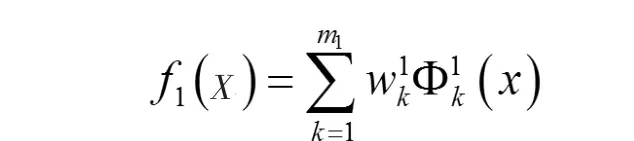
这里

表示权重,使用最小二乘法计算,使下列拟合残差平方和
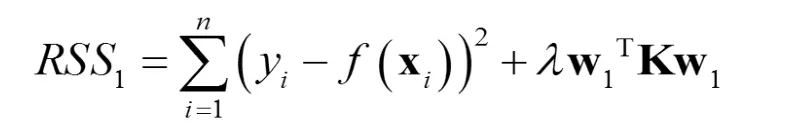
聚类时,我们采用了增广样本。这样得到的聚类
其中包含我们期望输出的信息,可以得到采用增广样本的径向基函数网络的精度高很多。 α1的取值不同,得到的聚类不同,网络的精度也不同,所以 α1也是一个需要优化的参数。
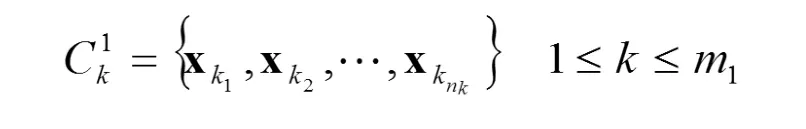
构建第二层的输出网络。首先计算第一层网络的拟合误差

然后把输入样本与前一层的误差项组合在一起,得到增广样本
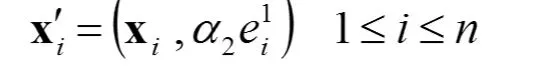
这里 α2>1。
然后再用 K-mean 法将
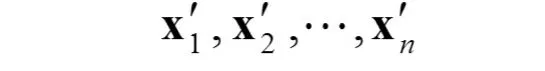
分成 m2个聚类
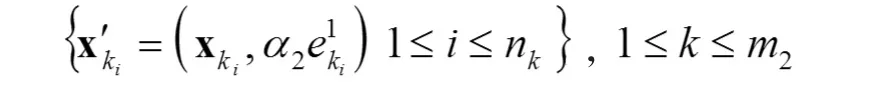
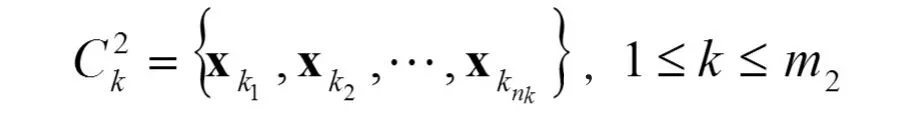
再 令 宽 度 系 数 为 d1, 其 中为 聚 类的 样 本 方差,而 d2是有待优化的参数。
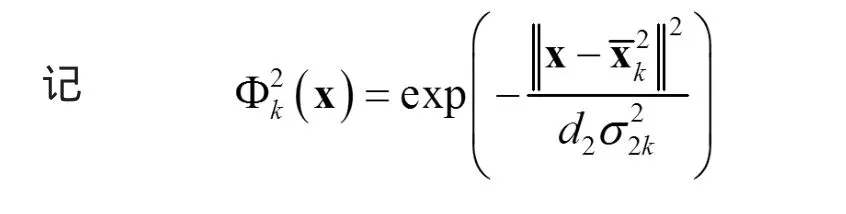
于是第二层网络的输出函数为
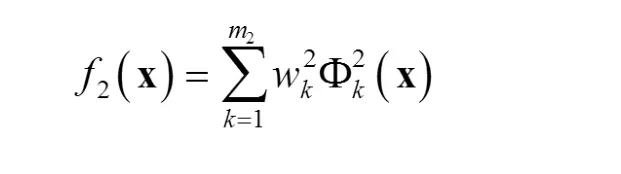
各个聚类的中心为
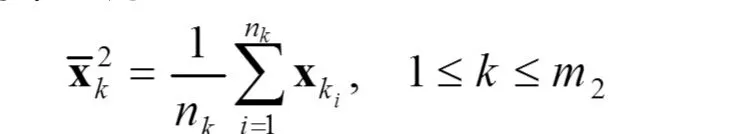
这样得到了 m2个新的样本聚类

可以得到第二层网络的加权系数的值。 若取 λ=0,则 W2为普通最小二乘法;若取 λ>0,则 W2为正则最小二乘法。

这样得到了一个更精确的模型

需要说明的是,在增广样本
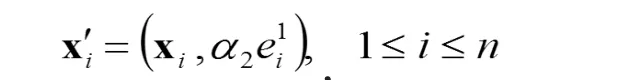

受到拟合残差的影响就小,所得到的函数 f2(X)对残差的抵消作用就小。 α2也是要优化的。

循环往复计算每一层网络,把每一层网络相加,最后可以构建一个高精度的径向基函数神经网络。

1.2 复合多层 RBF 网络构建原理
在上述聚类算法中,函数在每一个聚类上的值用一个径向基函数来逼近。这样网络的逼近精度是有局限的。 于是,做出改进,将一个聚类中的每个样本都看成一个径向基函数的中心,一个样本对应一个径向基函数。对每个聚类,我们构建一个子 RBF 网络,每个径向基函数的中心就是这个聚类中样本。
设 Ck是一个聚类,Ck中的样本记为

于是这个子 RBF网络为
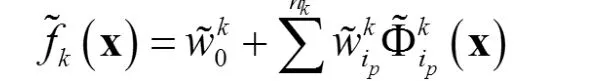
其中
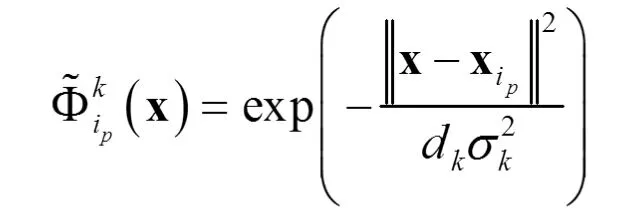
记权重向量为
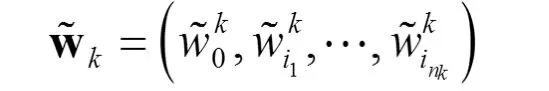
定义残差平方和

若 λk>0,则得正则最小二乘解
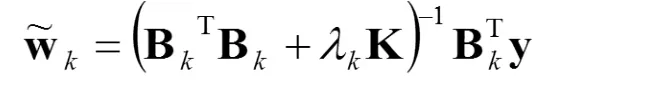
若令 λk=0,采用广义逆矩阵法,得最小二乘解

其中
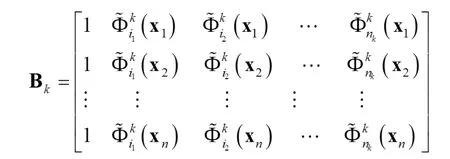
子网络的 GCV 计算公式如下:

其中,
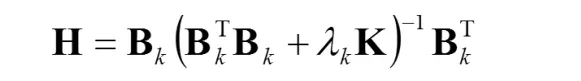
子网络的参数 dk和 ap的优化是使 GCV 最小。
再把得到的所有这些子网络整合起来。设共有K个子网络,整个网络就是输出的加权和

当 X取遍所有的样本时,得到
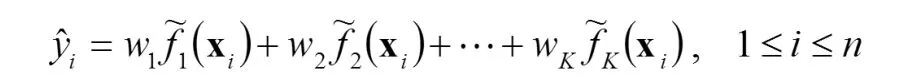
令

于是就得到了 的最小二乘解,

这样整个网络构建完毕。
2 变量和样本数据的选取
文中选取的输入变量包括 10 项, 用 xi表示;输出变量 1 项,用 y 表示。 具体如表 1。
文中采用某商业银行的个人贷款数据。为保证数据的普遍性进行再选择,目的是调整 y=0 和 y=1的数据选择比例。由于整体样本数据数量大,数据结构比较多样,差异比较大,因此采取分层抽样的方法,先依照是否给予贷款将整体分成为两份,然后从每一组中随机抽取 400 个样本, 从而使两者之比近似为 1∶1。 最终得到 850 个数据,其中训练学习数据包括 420 个样本;其余 430 个样本构成检验数据,用于单一模型的训练学习和检验。最后用单一模型的结果计算作为组合模型的输入变量。

表1 输入变量和输出变量
3 模型的构建
3.1 多元线性规划模型
建立因变量y 对自变量 xi的线性回归模型方程为:
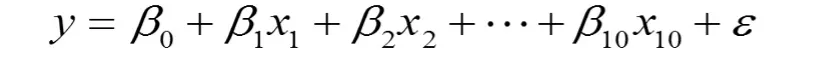
在建立理论回归模型方程后,利用已有的训练数据,使用 Stata 软件进行计算。 在本文中,采用显著性逐级检验分析进行多元线性回归分析,结果自变量x1,x3,x6,x9通过了显著性检验,得到的回归方程为:
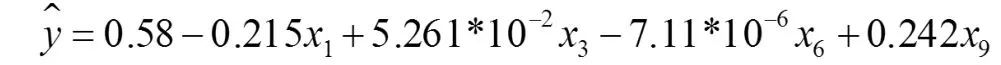
从上述模型可以看出,能否获得贷款y与模型中自变量 x1,x3,x6,x9联系相对较大。 并且通过方程可以看出与自变量 x3,x9为正线性相关的关系;与x1,x6,为负线性相关的关系。 通过 Stata 统计软件中的 z检验和 t检验对方程的系数和方程整体的显著性进行检验,结果均显著成立,表明方程建立成功。
3.2 Logistic 回归模型
建 立因变 量 y 对自 变量 xi的 logistic 回归模型方程为:
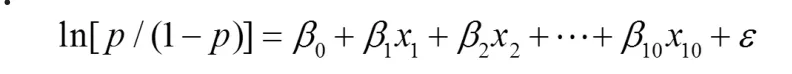
从模型可以看出:贷款能否取得y也是与模型中的自变量 x1,x3,x6,x9联系相对较大。 该模型的样本决定系数 R2为 0.82,取得了很好的拟合效果。
3.3 复合多层 RBF 网络组合模型
组合模型的基本原理如下:
yt(t=1,2, … ,n) 表 示 实 际 观 察 值 ;yit(i=1,2, … ,m;t=1,2,… n)表 示 第 i 种 方 法 的 预 测 值 ;则 eit=yt-yit(i=1,2,…m;t=1,2,…n)表示第 i种预测方法对第 t个数据进行预测时的误差。
若用m种方法进行组合预测,设各预测方法的系数分别为 k1,k2,…,km,km,满足

本文中把误差平方和 RSS 最小作为评定组合预测模型最优的标准,既求 k1,k2,…,km-1,km,使取得最小值。 其中均方根误差 RMSE,平均绝对误差MAE也在本文中列出作为比较。 根据多元函数求极值的方法,用 Q 分别对(i=1,2,…,m)求导,求 得驻点(使取得极小值的点)。 再加上限制方程 k1+ k2+…+km-1,km=1。 就可解得的 k1,k2,…,km-1,km。
本文选定神经网络核函数第一层个数为 40,以后各层为 120 个。 在训练的过程中依据网络层数从少到多的变化,观察误差的变化,学习速率会很明显的优于单层径向基函数网络。 在复合多层 RBF 网络设计的过程中,关键是增加网络层数。随着径向基函数网络层数的不断增加,每一层网络对前一层网络的误差进行拟合,这样使得神经网络的误差降到一定的程度,最终使得多元实函数和 Logstic 模型组合预测的步长和精度大大提高。 当预测步长达到 32时,预测误差超过控制线 0.03。 本文训练的误差变化情况如图1。
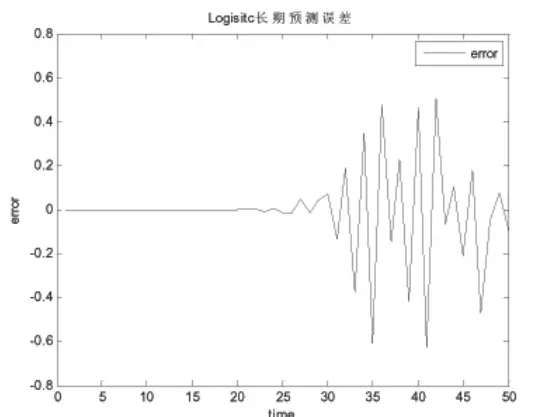
图1 复合多层 RBF神经网络训练误差曲线
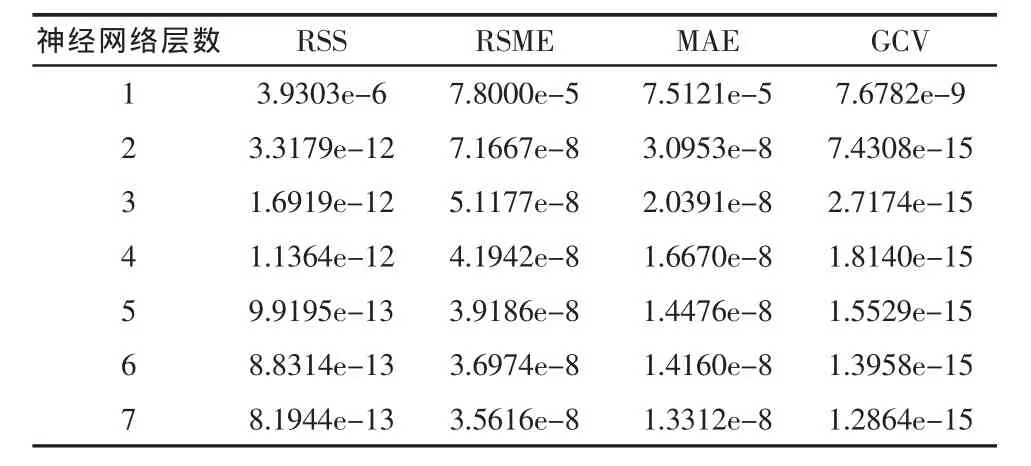
表2 复合多层 RBF网络每一层的训练误差

表3 复合多层 RBF网络的预测结果
由表2和表3可知,复合多层径向基函数网络的训练层数达到 7 层,训练误差达到 8.1944e-13,预测误差达到 7.8981e-14,实现了训练的目的。
4 结果分析
通过构建的复合多层径向基函数网络,对预测精度的比较,来评价所构建的3个个人信用评估模型。 为了保持数据的一致性,本文选择 3个模型中均使用的后 430 个,模型的预测结果作为评定的基础。需要说明的是前2种方法在判定贷款者的类型的时候,是以 0.5 作为临界值的,即将预测值大于等于 0.5称为信用好,反之则认为信用不好。比较结果见表 4。

表4 3种个人信用评估方法的预测精度的比较
由表4可以看出,基于复合多层径向基函数网络的多元线性回归和 Logistic 回归的组合预测模型,预测准确率远比2个单一模型的准确率高很多。在实际操作过程中,要尽量避免将无法按期偿还贷款者当成能够按期偿还贷款者发放贷款,这样会导致坏账的形成。复合多层径向基函数网络组合预测模型将犯此错误的概率由多元线性回归模型的 7.2%和 Logistic 回归模型的 6.7%和单层径向基函数网络组合模型的 6.2%,降低到 4.3%。 这在实际操作过程中规避信用风险具有更大的实际意义。
上述结果足以表明,复合多层径向基函数网络组合预测模型,更加优于多元线性回归和 Logistic 回归模型,组合预测可以作为个人信用评估的可供选择的更为精确的方法。
[1]石庆焱,靳云汇.多种个人信用评分模型在中国应用的比较研究[J].统计研究,2004,20(6):43-47.
[2]Moody J,Darken C.Fast learning in networks of locallytuned processing units.Neural Computation[J].1989,16(1): 281-294.
[3]Chen S,Cowan CFN.and Grant PM.Orthogonal least squares learning algorithm for radial basis function networks[J].IEEE Transactions on Neural Networks,1991,2(2):302-309.
[4]Chen S,Cheng ES,Ai Kadhimi,K.Regularized least squares learning algorithm for constructing radial basis function networks [J].International Journal of Control,1996,64 (5):829-837.
[5]Guang-bin H,Saratchandran P,Sundararajan N.A generalized growing and pruning RBF (GGAP-RBF)neural network for function approximation [J].IEEE Transactionson Neural Network,2005,16(1):57-67.
[6]Broomhead DS,Lowe D.Multi-variable functional interpolation and adaptive networks.[J].Complex System,1988,2(2): 321-335.
[7]王凌,郑大钟.径向基 函数神经网 络 结 构 的 混 合 优 化 策 略[J].清华大学学报:自然科学版,1999,39(7):50-53.
[8]陈政,杨天奇.基于 RBF 神经网络的股票市场预 测[J].计算 机应用与软件,2010,27(6):108-110.
[9]王春峰,万海晖,张维.组合预测在商业银行信用风险评估中的应用[J].管理工程学报,1999,13(1):5-10.
责任编辑:胡德明
Research on Composite Prediction Based on Composite Multilayer RBF Neural Network——Taking Rural Credit in Commercial Banks As an Example
Sheng Guomin1,Zhuang Jian2
(1.Tianchang Branch,Agricultural Bank of China,Tianchang 239300,China; 2.School of Business,Anhui University of Technology,Ma'anshan 243032,China)
For solving the problem that the multiple linear regression and logistic regression are not highly accurate in prediction and with the idea of combination prediction,the prediction method of combining multivariate linear regression and logistic regression by developing and using composite multi-layer RBF neural network is proposed and applied to personal credit evaluation of commercial banks.The results show that the combination forecasting method can obtain higher prediction accuracy than single RBF network method and regression method.
multiple linear regression;logistic regression;compound multilayer RBF neural network; combination forecasting;personal credit evaluation
O241
:A
:1672-447X(2017)03-0014-05
2016-12-28
盛国敏(1989-),安徽天长人,中国农业银行安徽滁州天长市支行经济师,研究方向为机器学习及应用;
庄健(1957-),上海人,安徽工业大学商学院博士研究员,研究方向为机器学习。
