基于“退位减法”前测分析的教学对策

◇董景勋

基于“退位减法”前测分析的教学对策

◇董景勋

一 缘起：做对了，但是不明白

在一次常态课教学中，和学生一起学习被减数中间和末尾有0的退位减法。我在黑板上出示500-348，让学生独立计算，然后指定个别学生上台讲解计算过程。待学生讲完后，我在旁边引导：“十位上的数相减为什么等于5？”学生A回答：“十位上是0，从百位退1，因为又向个位退1，所以就是9。”我接着追问：“你们听懂了吗？”大约过了十几秒，有个小手慢慢地举起来。举手的学生B说：“我没算，但是我不明白，0上有退位点，怎么变成9了呢？”学生的回答让我陷入了沉思：学生为什么不能理解呢？是否我们在教学中忽略了什么？

二 深入调查

在退位减法中，不够减时要从前一位退1，在这一过程中，往往会出现一些问题。上述现象，是我们班的个别现象，还是普遍存在的呢？基于此，我进行了针对整个年级的调查。调查对象是泰顺县仕阳镇中心小学三年级4个平行班共145个学生。调查内容如下。

1.列竖式计算。

（1）500-298= （2）350-149=

（3）409-314= （4）114-107=

（5）135-46= （6）203-193=

（7）814-737= （8）423-269=

（9）1000-591= （10）6375-486=

（11）403-158= （12）1010-999=

2.选择题。

（1）在计算 500-298时,点退位点的顺序是（ ）。

A．先点十位，再点百位

B．先点百位，再点十位

C．没有顺序

（2）如图1，圈出部分所代表的数值是（ ）。

图1

A．2 B．1 C．12 D．11

（3）如图2，圈出部分所代表的含义是（ ）。

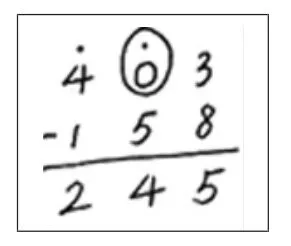
图2

A．10-1 B．9+1 C．没有含义

总体来说，有的需要连续退位，学生很不适应，所以解这类题的错误率比较高，如列竖式计算第（7）题的错误率高达35.86%；选择题第（1）题考查点退位点的顺序，是学生理解的难点，所以该题的错误率为14.48%；选择题第（2）题考查退位点表示的含义，是学生容易混淆的内容，所以该题的错误率为24.13%；有的题目中，被减数中间有0，需要从高位退1，学生理解起来较困难，错误率较高，如选择题第（3）题的错误率高达37.93%，列竖式计算第（9）题和第（12）题的错误率都是28.97%。

退位点有两个含义，第一个含义是向后一位退1，第二个含义是加上原位上的数。学生往往忘记加原位上的数，这种错误率在30%以上。另外受退位负迁移的影响，学生没有真正感受到退位的必要性。有时候只需要退一次却退两次（如图3百位上的0-5）；有时候需要退位却没有退位（如图4）；有时候不需要退位却退位（如图5）；忘记加原位上的数（如图6）；1和 0退位后含义混淆（如图7）；忘记连续退位（如图8）。

图3

图4

图5

图6

图7

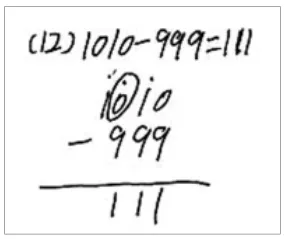
图8

三 成因分析

问卷中的第一题是基于教材的变式题，第二题是根据学生对退位点的理解改编的。我们不难发现，在计算过程中，学生经常出现计算不仔细的情形，这已经不是简单地用“粗心”两个字所能涵盖的了。

1.单一的思维与复杂的综合思维的矛盾。

二三年级的学生思维方式比较单一，但是算式背后每个数位上数的变化都需要算理的支撑。何时退位，怎么退位，都需要经过多重思维路径的思考才能得到最终的结果。如人教版教材三年级上册第四单元“万以内的加法和减法（二）”中的第二节三位数连续退位减法，其中十位、百位、千位上的数相减，既要从高位退1作10，加上原位上的数，还要减去退向低位的1后再减，构成了复杂的综合思维与计算过程，思维比较单一的三年级学生容易顾此失彼，从而出现错误。

2.推理过程和计算环节烦琐，与计算自动化能力的矛盾。

退位减法教学过程中，常常隐藏很多计算的策略、操作程序，如上面所述学生暴露的问题：只需要退一次却退两次，不需要退位却退位，忘记加原位上的数，1和0退位后含义混淆等。但是我们在教学中往往会要求学生减少运算步骤，简化运算过程，达到自动化计算，以提高运算速度。

3.教学的疏漏。

（1）教师急于总结算法。

对于计算，教师追求的往往是准确与快速。受教学时间的限制，教师经常在规定的教学时间内，摒弃烦琐的方式，用自己的语言“拐杖”帮学生梳理算理，提炼算法，从而替代学生的思考。殊不知这些简捷而规范的竖式往往是不容易理解的。或许呈现一些表面看起来不简捷，但是由学生自然生成的竖式作为过渡，对于帮助学生理解计算过程中的原理会有好处。

（2）学生退位动机不深刻。

退位意识的建立需要借助问题，也可以是生活的需要。如对于51-36这一算式，教材会辅助提出退位动机的需求：个位上1减6不够减，所以需要从十位退1。然而在实际教学中，有部分学生另寻一条路：有的把51看成56，用56减去36，等于20，再减去5；也有的从高位算起直接避开退位，先用50减 30，然后用21减去6等于 15；等等。学生总是有多种方法解决它。如果教学时仅仅提倡一种方法，忽略学生的多种方法，缺少对每种方法的比较、辨析，退位意识就很难深刻地植入学生的脑子中。

（3）批改时没有深入分析错误原因。

当学生出现结果错误、选择方法错误时，教师往往不够重视，轻易地判定这是“粗心”引起的，只是轻轻松松地打个叉，让学生去订正。这样“粗心”就成了学生做错题目的一个理直气壮的借口，之后他的作业中是不是会继续出现更多这样的“粗心”呢？

四 教学对策

《义务教育数学课程标准（2011年版）》指出：课程内容的组织要重视过程，重视直观，处理好直观与抽象的关系。数学的算理经验需要在“做”的过程和“思考”的过程中积淀，是在不断经历、体验各种数学学习活动的过程中逐步积累的。

1.内容呈现：从模糊到清晰。

在基本技能的教学中，组织学生尝试计算活动，引导学生观察、分析、抽象概括，运用知识进行判断，帮助学生理清相关知识之间的区别和联系，从而让算理从模糊到清晰。

（1）算式和图的类比。

案例一：百以内的退位减法。

活动一：根据数学问题（如图 9），列出竖式，尝试解决。

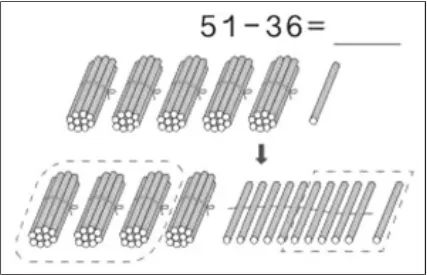
图9

活动二：根据图动态解释算理。

通过列竖式的方式，我们很清晰地看出每一步的计算过程，得出结果。那么，你们能看懂图9吗？能发现什么？

（2）竖式与竖式之间的对比。

在上面的案例一中，不同的学生在计算时呈现出不同的思维路径，教师应让学生通过对比、观察，发现两个竖式的区别和联系。

比较一：如图10，在计算方法上，前者是从高位算起，后者是从低位算起。

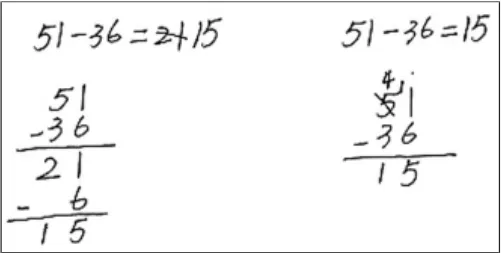
图10

比较二：如图11，在计算过程上，前者是先加后减，后者是先减后加。

图11

比较三：如图12，前者是清楚的退位过程，后者是简约的退位方法。

图12

学生的思维方式是多元的，对于很多计算方法，若教师不去细细思考，就很容易错过其对学生的引领价值。受口算的影响，有的学生产生了从高位算起的方法；还有的另辟蹊径想到用整数去减一个数，于是先减后加；还有的直接简化了退位过程。通过引导学生对从高位算起与从低位算起的比较，他们才会明白从低位算起的优势，才会重视计算的“序”。

2.算理呈现：从表面到深入。

让教学慢下来，使学生充分经历活动过程，感悟算理，常用的方法是利用学生已有的数学知识、经验，借助直观，使学生在操作和观察的过程中感知，获得表象，进而内化为算理。

抑制控制指注意力集中于相关的信息并加工过程，同时抑制无关的信息和过程，是执行功能的核心成分之一。常用Stroop测验、Go/Nogo任务反映执行功能抑制性控制的测验。Simonsen等[20]的研究中显示,双相Ⅰ型和双相Ⅱ型均存在抑制控制，且双相Ⅰ型损害更严重；而Gruber等[21]研究缓解期的双相抑郁和双相躁狂的抑制控制均有改善，且前者改善较显著。

（1）画图——直观图让算理外显。

在被减数中间或末尾有 0的退位减法中，如500-133和500-403，让学生尝试计算后，用画图的方法表示自己的计算过程，如图13所示。

图13

画直观图是指利用图形描述和分析问题。学生画直观图表示每一次退的过程，这样可使退位的思维过程外显出来。

（2）拨珠子——让算理有支撑。

借助计数器说明连续退位，可以清晰地呈现各数位上数的变化情况，帮助学生掌握连续退位减法。用边拨计数器、边提问、边启发的形式，将笔算过程展示出来。

案例二：万以内的退位减法。

出示图14：

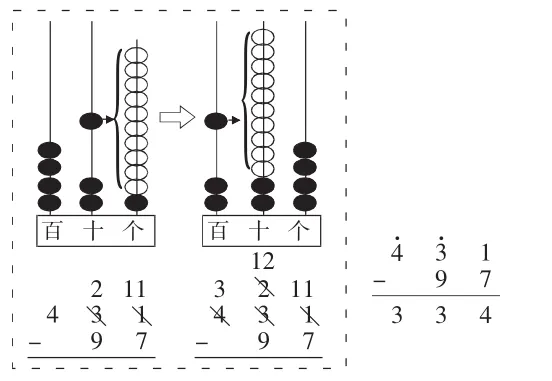
图14

教师边在计数器上演示边讲解：个位上1减7不够减，从十位退1。随后教师从十位上拨去1个珠子，并在竖式上把十位上的3画去，在它的上面写上2。

问题二：从十位退1给谁？是几个几？

学生回答后，教师往个位上拨10个珠子，和原位上的1个珠子合起来就是11个珠子，在竖式的个位上将1画去，在它上面写上11。

问题三：现在个位上是几？够不够减7？

学生回答后，教师从计数器的个位上拨去7个珠子。

问题四：十位够减吗？如果不够减，从哪一位退1？百位上的4怎么办？

问题五：从百位退1给谁？现在十位上一共有几个珠子？

学生回答后教师画去2，在2上面写12，然后从十位上拨去9个珠子。

待学生完整地用竖式计算一遍后，请学生回答：退位后每一位上分别是几减几？为什么？

教师示范竖式的书写格式，并指出平时计算时除了退位点，退位过程一般不写。

整个过程，教师始终把计数器演示和竖式对照，直观揭示了个位、十位上数的变化，旁边有完整的竖式，既有计算的思考过程，又有计算的结果，分散了学习难点，便于学生掌握。

（3）举例子——让算理落地。

很多数学内容都能在生活中找到支撑，即找到情境原型。应用情境会降低算理理解的难度。

案例三：“百以内数的加减法”教学片段。

出示情境：小明有3元钱，买本子用去6角4分，还剩多少钱？（以分为单位列式）

学生列出算式300-64。然后尝试用学具操作解释。

生：我先把1元换成10角，再从10角里拿出1角换成10分。

教师要求学生脱离情境，同桌之间互相说一说。

辨析和交流：为什么末尾两位上都是0，个位上是10-4，十位上却是9-6？

借助元、角、分解释算理，使连续退位过程生动、形象地展现在学生面前，学生容易感知，容易理解。

（4）描述——将算理表述出来。

呈现不同算式，给学生充分的时间和空间，让他们用自己的方式表达算式背后的算理。

①利用颜色，说一说。

边说边思考是算理外化的一种形式。利用不同的颜色加以区分，有效避免了计算顺序和数位变化的混淆。如分别用蓝色和绿色代表退位的变化和位值，将每一次计算的数位用颜色重点突出，提醒学生当前的计算数位及计算顺序。

②利用补白，写一写。

与说相比，用文字把思维过程写出来，由于经过了更多的整理和外化，所以在写的过程中增加了调整的机会。如在“百以内的退位减法”中，对于“52-17”，让学生尝试列竖式计算。出示图15：在方框里填写位置值，用虚线上方的空白代表数位上数值的变化，这样的留白填写可以使学生真正体会到退位的含义。

图15

③利用斜线，画一画。

与写相比，把思维过程画出来，更能显示出解题的结构。比如，画斜线等，简单明了地对减法运算过程进行演示，如图16所示。

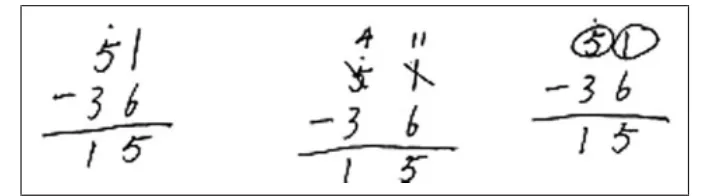
图16

3.练习呈现：从片面到全面。

（1）加强对退位意识的培养。

在低年级的退位减法练习中，教师应该设计相应的练习，利用数位制与数分解的原理，引导学生养成退位意识，为高年级抽象的思维计算打下基础。如图17，动态的一步步从左到右的引导，可帮助学生计算。

图17

（2）练习中设计补全竖式中的空白问题。

这样做，一方面，可以锻炼学生利用加法与减法互为逆运算进行转化的能力；另一方面，也能锻炼学生的逆向思维能力，发展学生的数学思维能力。如图18，对于同一个算式，先让学生完成左边的部分，然后改变补白位置，从而让思维走向全面。

图18

［1］范存丽.让数学思维过程“看得见”［J］.人民教育，2014（15）.

［2］刘北荣．突破连续退位减法的难点［J］.云南教育，1997（5）.

［3］许勇.“连续退位减法”的教学反思［J］.中小学数学（小学版），2012（7/8）.

［4］瓦尔.借助元、角、分教连续退位减法［J］.湖南教育，2002（4）.

（作者单位：浙江泰顺县仕阳镇中心小学。作者系朱乐平名师工作室“一课研究”团队成员）