高超声速进气道前缘流场-热-结构耦合分析

张胜涛, 陈 方, 刘 洪

(1.上海交通大学, 上海 200240; 2.中国航发商用航空发动机有限责任公司, 上海 200241)



高超声速进气道前缘流场-热-结构耦合分析

张胜涛1,2, 陈 方1,*, 刘 洪1

(1.上海交通大学, 上海 200240; 2.中国航发商用航空发动机有限责任公司, 上海 200241)

通过分析高超声速流场-热-结构耦合问题的机理过程，对多场耦合模型进行了数学物理描述，以此发展了松耦合分析策略框架。在此基础上，采用自适应耦合计算时间步长、混合插值策略和复杂外形网格变形等方法，实现了多场耦合分析平台。针对高超声速飞行器进气道前缘结构的耦合特征进行了初步分析研究，计算结果揭示了在持续长时间飞行条件下流场-热-结构耦合的时空分布特征，为深入开展高超声速飞行器热防护系统的综合性能评估及优化提供了理论与技术支撑。

高超声速流动；进气道；流场-热-结构耦合；热防护；自适应耦合步长；耦合策略；激波相互作用

0 引 言

当高超声速飞行器在近空间大气层内进行远程机动飞行时，将面临具有复杂流场、高焓、中低热流和持续长时间气动加热等特征的气动热力学环境。尽管面临的飞行环境如此恶劣，但是高超声速飞行器的热防护设计要求却极为苛刻，即在满足重量尽可能轻的约束条件下实现高效、可重复使用的非烧蚀热防护。这些苛刻要求对热防护系统综合性能优化提出了严峻挑战。为了实现更合理的结构选材和防热优化，最大限度减小热结构设计冗余，必须更准确地预测飞行器的热力环境特性。 由于高超声速飞行器采用机身/发动机高度一体化设计，其在近空间大气层内进行持续长时间、宽马赫数域的远程机动飞行过程中，外部流场的气动力/气动热和内部结构的传热/应力/变形等各物理场间的相互作用将变得极为强烈。因此，要准确地预测飞行器的热力环境特性，必须统筹考虑流场、热和结构等各物理场间的相互耦合关系，建立多场耦合一体化分析方法，从而为高超声速飞行器热防护设计提供有效的理论与技术支撑。

国外学者Thornton, Dechaumphai和Wieting等人[1-3]最早提出了流场、热和结构之间多场耦合问题，并基于双向耦合方法发展了流场-热-结构一体化有限元方法，为分析更为真实复杂的多场耦合问题奠定了基础。其后，相继发展了迭代耦合方法[4-5]和基于分区耦合方法的交错策略[6]以及将非稳态问题看成由一系列“准稳态问题”的混合耦合策略[7]和统一求解耦合策略[8]。为了进行高时间精度的流场-热-结构耦合分析，Miller等人[9-10]采用多循环方法发展了基于松耦合的多物理时间推进策略。国内学者黄唐和毛国良等人[11]率先研究了基于松耦合策略的流场、热和结构一体化数值模拟方法。随着对于持续长时间气动热力环境下流场-热-结构耦合问题重要性的认识，陆续开展了流场、热和结构多场耦合计算研究和分析[12-19]。随着高超声速飞行器研制的不断发展，多场耦合分析的思想和应用逐渐深入到工程实际，但是对于复杂热力环境作用下的多物理场耦合特征和规律的认识还不够深入，相关耦合性分析方法有待进一步发展和完善。

本文首先通过对高超声速流场-热-结构耦合问题的机理过程分析，提出了基于稳态飞行的松耦合分析策略，然后在此基础上发展了高超声速流场-热-结构耦合分析平台HyCCD (Hypersonic Coupling Computational Dynamics)，最后针对激波相互作用下的高超声速进气道前缘结构进行了流场-热-结构耦合计算分析研究。

1 耦合分析策略

1.1 流场-热-结构耦合模型

高超声速流场-热-结构耦合问题的耦合机理是流体介质内的流场气动力/气动热等物理属性和行为与固体介质内的结构传热/应力/变形等物理属性和行为通过流-固耦合界面发生相互作用和影响的物理过程。因此耦合策略的制定既需考虑流体介质与固体介质之间特征参量的面耦合，也需考虑它们各自内部特征参量的体耦合，为此本文考虑如图1所示的高超声速流场-热-结构耦合模型。

在流体介质内部，气动力/气动热之间的耦合由统一流动控制方程描述。利用计算流体力学(CFD)方法求解流动控制方程，获得流体介质内部的气动力/气动热参量，通过流-固耦合界面向固体介质提供热载荷(壁面热流q)和力载荷(壁面压力p)。在固体介质内部，结构传热/应力/变形之间的耦合由热传导控制方程和热弹性力学控制方程描述。考虑结构温度和变形的耦合效应，利用基于有限单元法(FEM)的计算热-结构动力学(CTD/CSD，或CTSD)统一求解热传导控制方程和热弹性力学控制方程，获得固体介质内部的热/力耦合响应参量，通过流-固耦合界面向流体介质提供温度条件(壁面温度T)和结构变形条件(壁面位移u)。

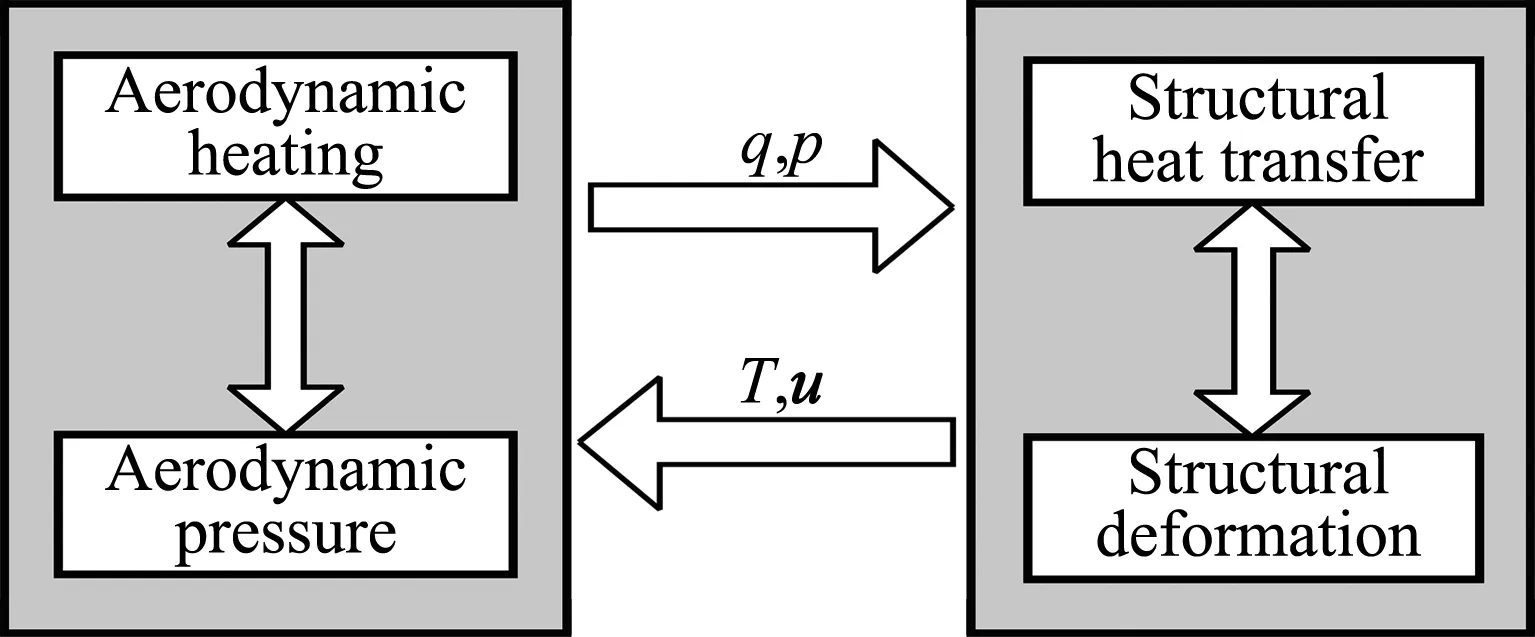
图1 流场-热-结构耦合模型Fig.1 Fluid-thermal-structural coupling model

1.2 基于稳态飞行的松耦合分析策略

基于上述流场-热-结构耦合模型，本文建立了如图2所示的基于稳态飞行的松耦合分析策略。图中，ΔtF为流场计算时间步长；ΔtTS为固体热-结构体耦合计算时间步长；ΔtC为流-固面耦合计算时间步长，可取为若干倍的固体热-结构体耦合计算时间步长，即ΔtC=nΔtTS，(n=1,2,3,…)。

图2 基于稳态飞行的松耦合分析策略Fig.2 Loosely-coupled analysis strategy based on the static trajectory

根据耦合物理过程的时间演化自适应地选取流-固面耦合计算时间步长ΔtC，对于持续长时间耦合计算分析效率具有重要意义。本文将耦合计算时间步长ΔtC的选取看作为一个自动控制问题，采用经典的PID(proportional-integral-derivative)控制器对耦合计算时间步长进行自适应控制[20]，则有：

(1)

式中：下标和上标“n”表示耦合时间步；TOL为人为给定的输入容差；KP、KI和KD为PID控制器的经验参数。本文采用文献[21]建议的数值，即KP=0.075，KI=0.175，KD=0.01；rn为耦合界面温度在tn时刻的变化度量：

(2)

为了防止耦合计算时间步长的过大或过小增长，引入如下步长限制为：

(3)

(4)

式中：Δtmin和Δtmax分别为人为给定的最小和最大耦合计算时间步长；m和M分别为人为给定的最小和最大步长增长率。

耦合策略的具体实施流程可以概述为：

1) 在初始t0时刻，首先给定固体域某一初始恒温或温度场分布以及初始受力和位移约束，然后通过界面信息传递方法将固体域的壁面温度和位移量传递给流体域，其中壁面温度作为流场计算的边界条件，而位移量用来更新流场网格；

2) 基于施加的温度边界条件和更新的流场网格，在流体域内进行稳态流场计算，最终得到稳态流场的壁面热流密度和壁面压力；

3) 通过界面信息传递方法将稳态流场的壁面热流密度和壁面压力传递给固体域，分别作为固体热-结构动力学计算的热载荷和力载荷；

4) 基于施加的热载荷和力载荷，在固体域内进行瞬态热-结构动力学计算，时间推进从t0时刻至t0+ΔtC时刻，最终得到t0+ΔtC时刻的固体结构热/力耦合响应参量；

5) 通过界面信息传递方法将t0+ΔtC时刻固体域的壁面温度和位移量传递给流体域，其中壁面温度作为流场计算的边界条件，而位移量用来更新流场网格； 6) 至此完成一个耦合计算时间步长ΔtC的计算，然后进入下一个耦合计算时间步长继续进行计算，以此类推直至整个耦合时间结束。

2 控制方程及数值方法

2.1 流动控制方程求解

考虑包含NS种组分的化学反应完全气体混合物，则可压缩粘性化学非平衡流动的Navier-Stokes控制方程组在笛卡尔直角坐标系下的守恒积分形式写为[22-23]：

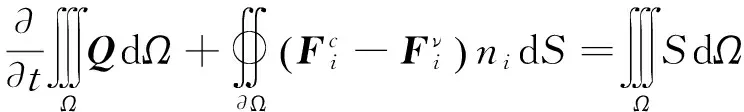
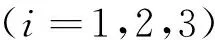
(5)

其中，

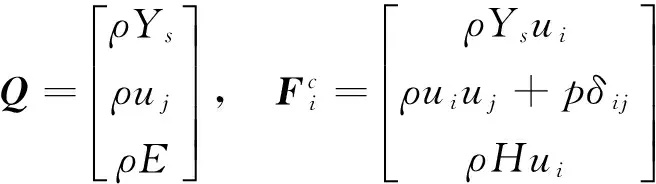
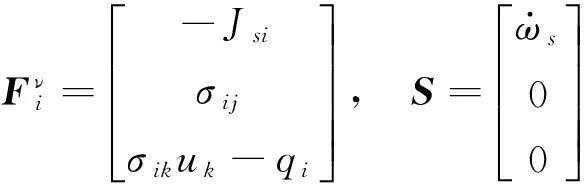
(6)

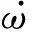
基于有限体积法对上述流动控制方程进行离散求解。其中，对流通量采用M-AUSMPW+混合迎风格式，并用多维限制器MLP提高至三阶精度；粘性通量采用二阶中心差分格式进行离散；时间推进采用LU-SGS隐式方法。为了加速收敛过程，采用当地时间步长和隐式残值平均等加速收敛措施。

2.2 热弹性力学控制方程求解

考虑结构温度和变形的相互耦合效应，利用有限单元法(FEM)进行统一耦合求解。将变分原理应用于热传导控制方程和热弹性力学控制方程以及它们相应的边界条件，最终可得到如下形式的有限单元矩阵方程为：

(7)

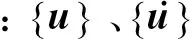
利用ANSYS Mechanical APDL完成热-结构耦合计算，采用的单元类型为SOLID226。该单元具有20个节点，每个节点具有五个自由度。对于热-结构耦合分析，节点自由度主要是三个方向的位移分量和温度。

2.3 界面信息传递方法

综合考虑反距离加权插值法[24]和径向基函数插值法[25]的特点和耦合变量(位移、温度、压力和热流)的物理特性，提出如图3所示的混合插值策略。壁面温度和位移量的传递需要满足其分布特性，采用反距离加权插值法；壁面热流和壁面压力的传递需要保证其插值前后的守恒特性，采用径向基函数插值法。同时考虑到在插值过程中线性方程组可能会出现求解失败，则采用反距离加权插值法以保证耦合计算的顺利进行。

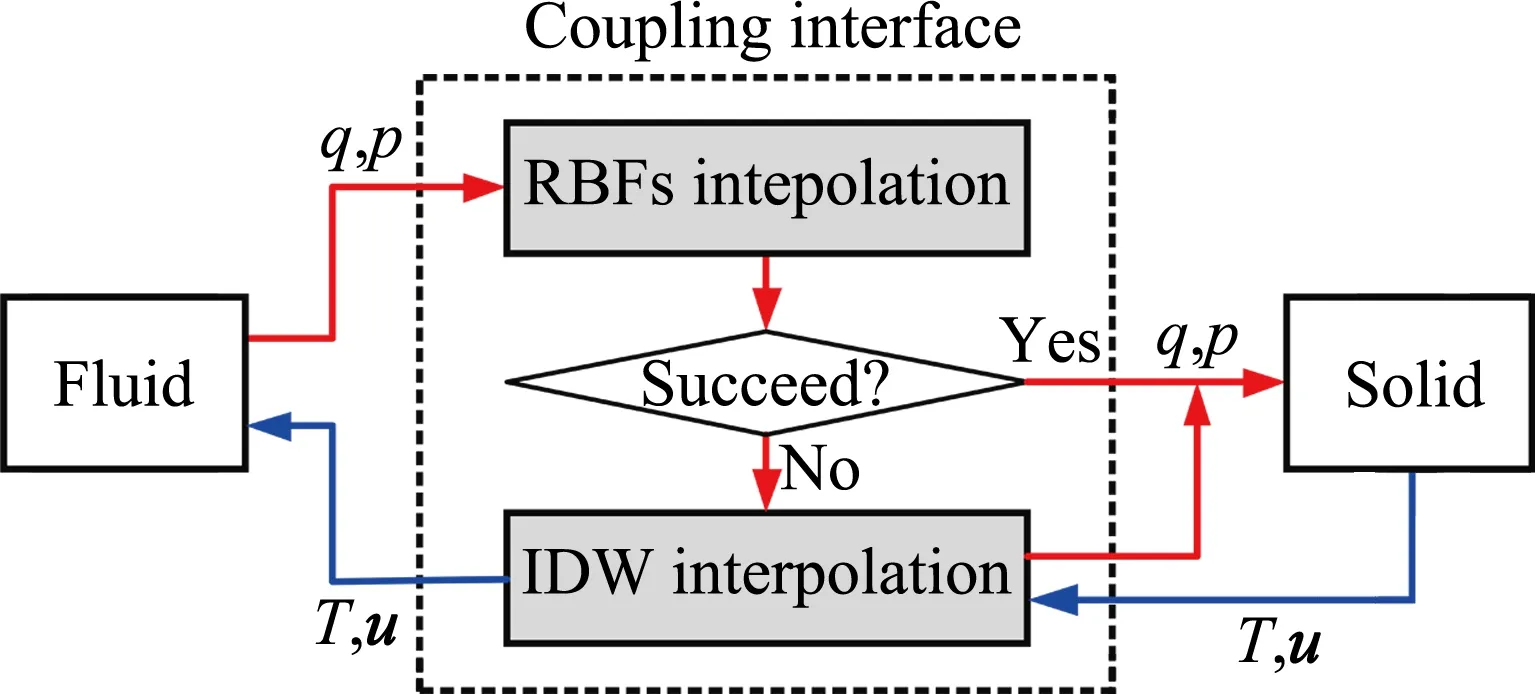
图3 流场-热-结构耦合问题的混合插值策略Fig.3 Hybrid interpolation strategy for fluid-thermal coupling problems

2.4 网格变形方法

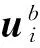
(8)

式中：NB为网格边界节点的个数；wi为距离权函数，其表达式为：

(9)

式中：dji为网格内部节点rj与网格边界节点ri之间的欧氏距离，dji=‖rj-ri‖，r为位置矢量；u为距离的幂次，取u=2。当所有网格节点的位移uj已知后，则可以更新整个流场网格：

(10)

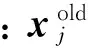
3 计算结果及分析

3.1 计算模型

高超声速飞行器前体预压缩斜激波与进气道前缘激波可能相交，产生复杂的激波相互作用，导致进气道前缘的气动加热问题变得更为严重。如图4所示，Case 1为超临界状态，斜激波入射在进气道唇口以内，进气道前缘处于远场自由来流条件；Case 2为临界状态，斜激波正好入射在进气道唇口上，与进气道前缘激波发生相互作用；Case 3为亚临界状态，斜激波入射在进气道唇口以外，进气道前缘处于斜激波波后的自由来流条件。本文以进气道前缘为计算模型，考虑Case 2工况，它包含Case 1和Case 3两种流动条件(见表1)，持续耦合计算时间为11 s。

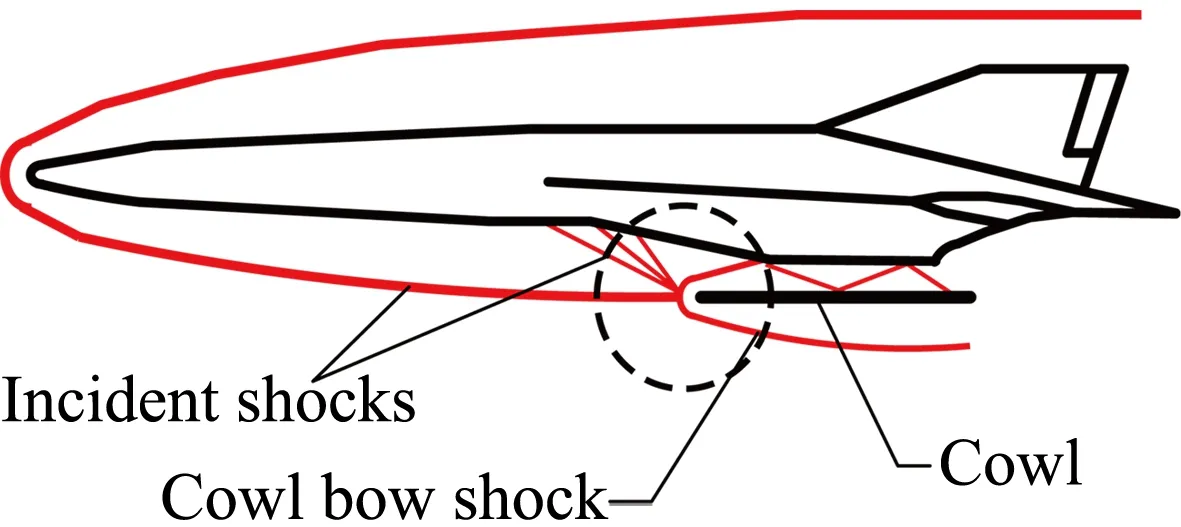
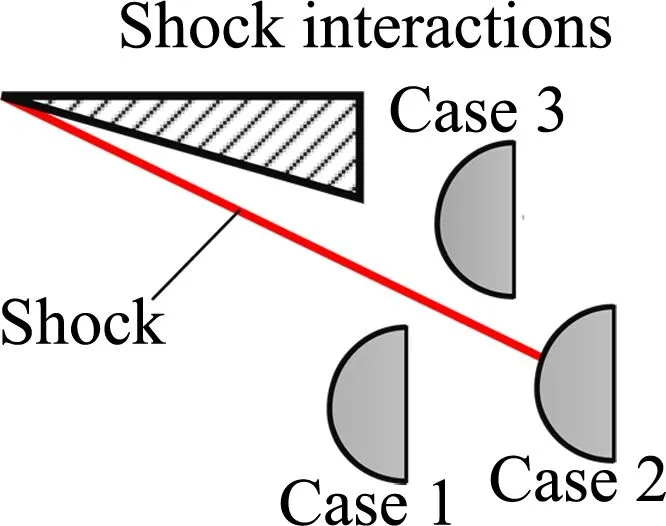
图4 高超声速飞行器进气道唇口激波相互作用现象Fig.4 Shock interaction phenomena near the cowl leading edge of hypersonic vehicles表1 进气道前缘模型来流条件Table 1 Freestream conditions for the leading edge

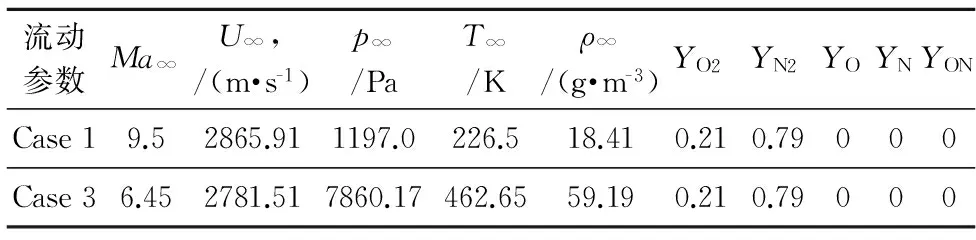
流动参数Ma∞U∞,/(m·s-1)p∞/PaT∞/Kρ∞/(g·m-3)YO2YN2YOYNYONCase19.52865.911197.0226.518.410.210.79000Case36.452781.517860.17462.6559.190.210.79000

外部流场计算采用化学非平衡气体模型，壁面为非催化条件；固体结构初始温度为300 K，初始应力为0，热应力参考温度为300 K。如图5所示，考虑外部流场的气动力/气动热载荷作用，同时考虑壁面的辐射效应，壁面发射率为ε=1.0；内壁面施加均匀分布的压力载荷p∞=1197 Pa；模型两端位置约束条件采用固支约束。进气道前缘的几何模型与文献[19]中的圆柱前缘模型相一致，CFD网格采用结构化划分，大小为201×111×11，在激波和近壁面附近进行加密处理；FEM网格采用非结构化划分，最小单元边长为0.5 mm。前缘材料采用钛合金，其物理属性见表2。

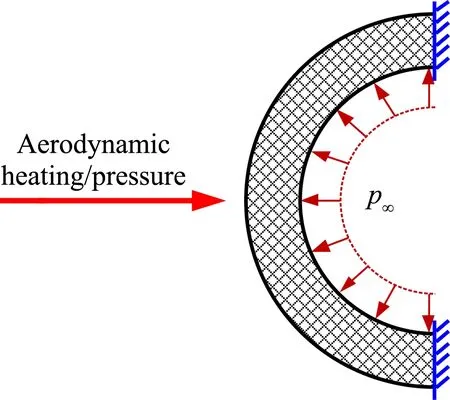
图5 进气道前缘模型的载荷和位移约束条件Fig.5 Load and displacement restriction conditions of the leading edge

表2 钛合金材料热-结构物理属性Table 2 Physical properties of Titanium alloy

3.2 初始流场

图6所示为该进气道前缘模型在初始t=0 s时刻的绕流流场结构云图。可以看出，其流场结构大致可以划分为远场自由来流区及其产生的弓形激波区、入射激波波后自由来流区及其产生的弓形激波区。在这两个弓形激波波后区之间产生由两剪切层形成的“流管”，导致壁面压力和热流密度出现很高的极值。如图7所示，相比于未受激波干扰的流动，激波相互作用使壁面压力系数增大约8倍，而使壁面热流密度增大约5倍。由此可见，这种激波相互作用现象的存在将极大地放大外部流场的气动力/气动热载荷作用，从而给飞行器热防护设计带来更为严峻的挑战。

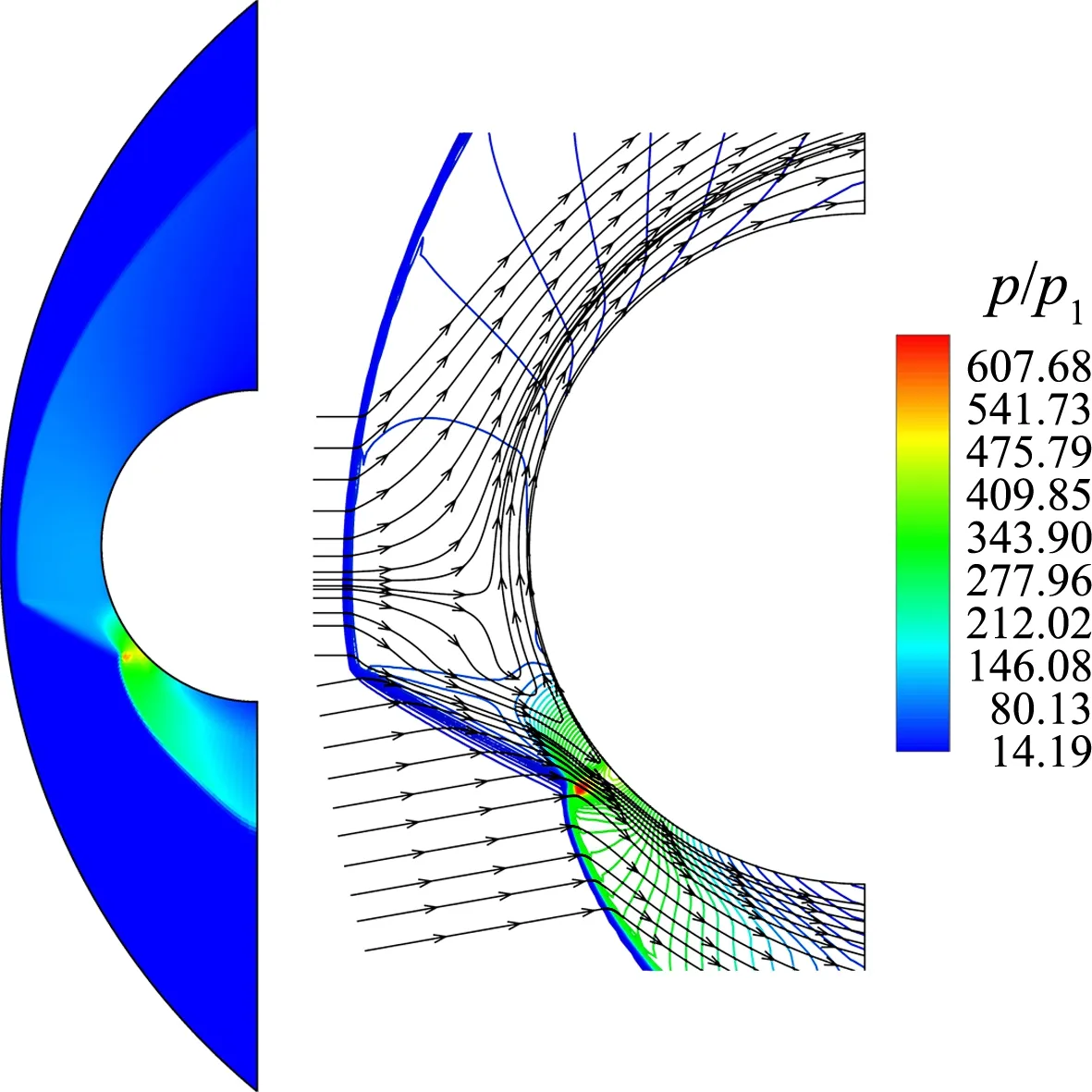
(a) 压强

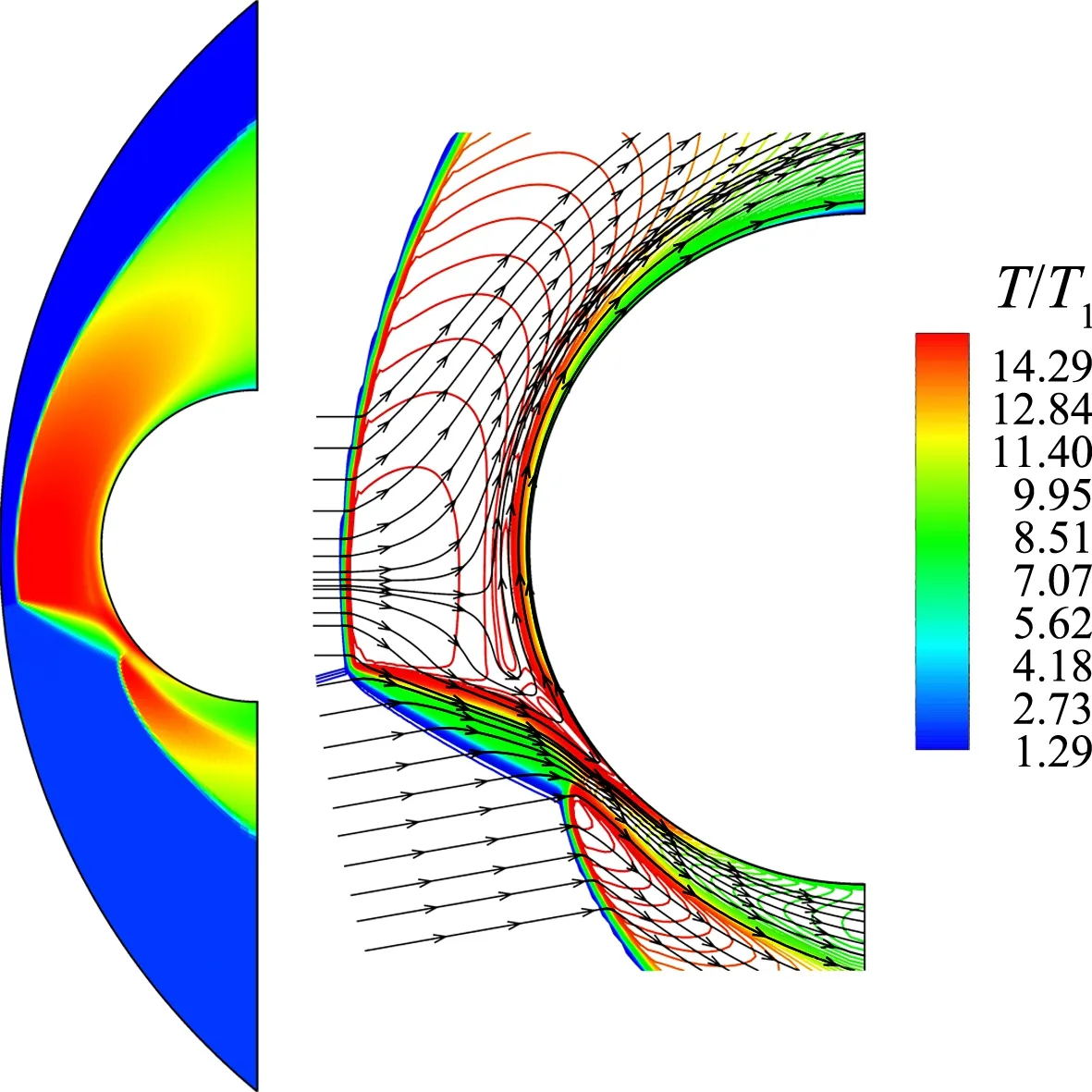
(b) 温度图6 进气道前缘模型初始时刻绕流流场结构Fig.6 Flowfield structure around the leading edge at initial time

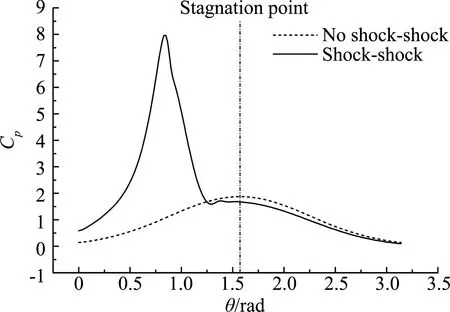
(a) 壁面压力系数

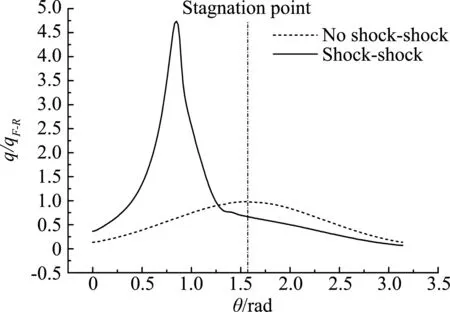
(b) 壁面热流密度图7 进气道前缘壁面压力系数和热流密度分布Fig.7 Wall pressure coefficient and heat flux of the leading edge

3.3 流场-热-结构耦合特性分析

图8所示为进气道前缘模型的壁面温度分布和变形量随时间的演化历程。由图8(a)可以看出，由于激波相互作用而导致的高热流犹如一道高强度能量束撞击在壁面上，引起壁面被撞击处的温度随时间迅速升高。在短短11 s时间内，考虑辐射效应的壁面温度最高点已达至初始温度的近8倍，远高于壁面驻点处的温度及其温升速度。同时也可以看到，在t=11 s时刻的壁面被撞击处的温升速度已经明显减弱，随着时间的再持续，该位置将率先达到热平衡状态，而其他部位的壁面温度会继续升高，直至达到热平衡状态。从图8(b)中可以看出，在激波相互作用导致的高热流作用区域，壁面变形随时间变化较快，变形量也最大；随着时间的持续，壁面变形量最大点逐渐由激波相互作用的部位向驻点偏移。

图9所示为进气道前缘模型的壁面热流密度分布和压力系数分布随时间的演化历程。壁面热流密度随壁面温度的逐渐升高而减弱，体现了流-固之间传热的耦合性；随着时间的不断持续，最终将会达到热平衡状态；而壁面压力受壁面温度变化的影响不大，随着时间的持续，壁面变形量逐渐增大，在壁面变形量最大区域，压力开始有所增大。

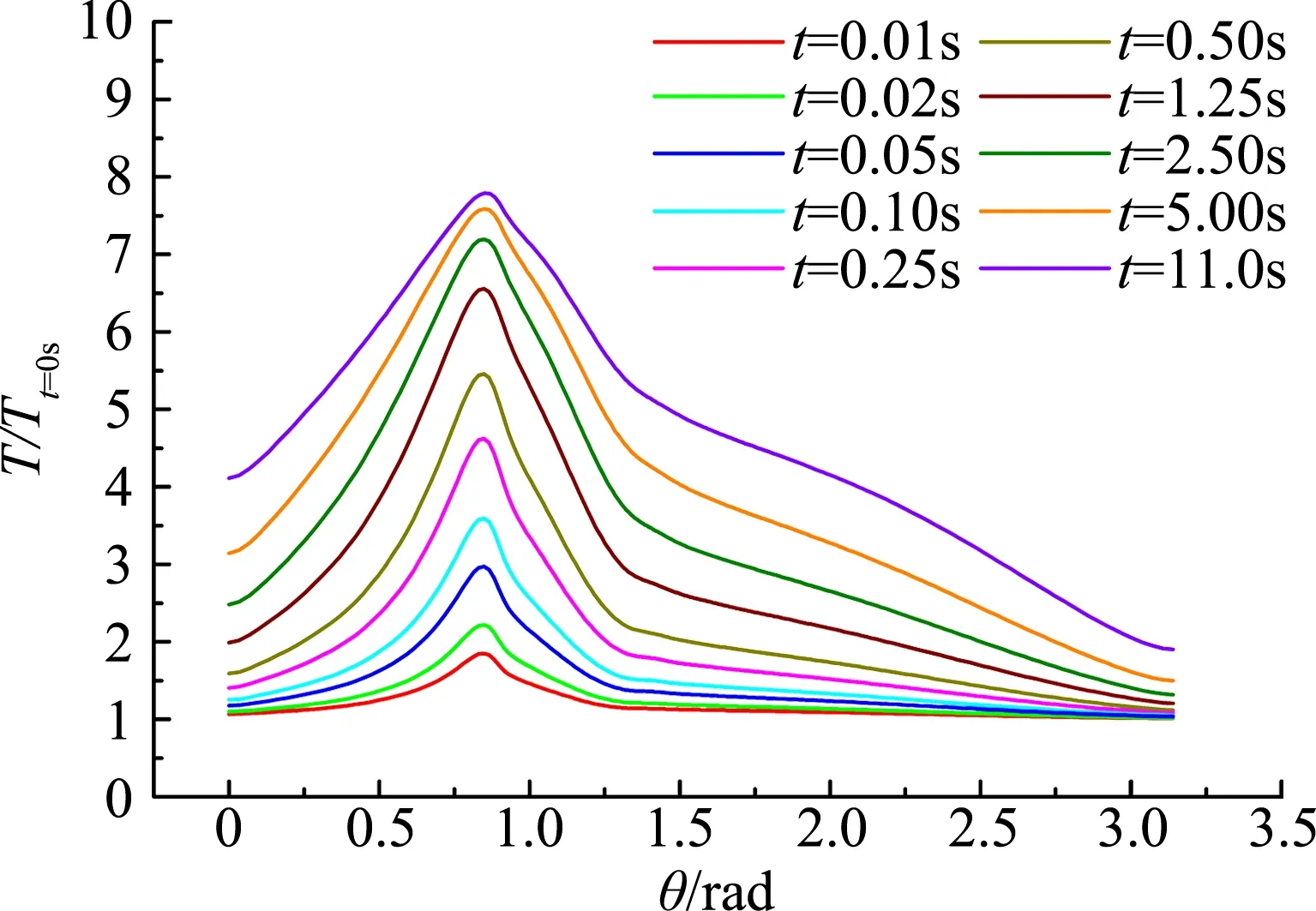
(a) 壁面温度分布

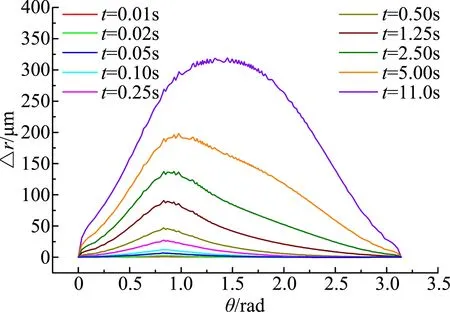
(b) 壁面变形量图8 进气道前缘壁面温度和变形量随时间的演化历程Fig.8 Time history of wall temperature and deformation of the leading edge

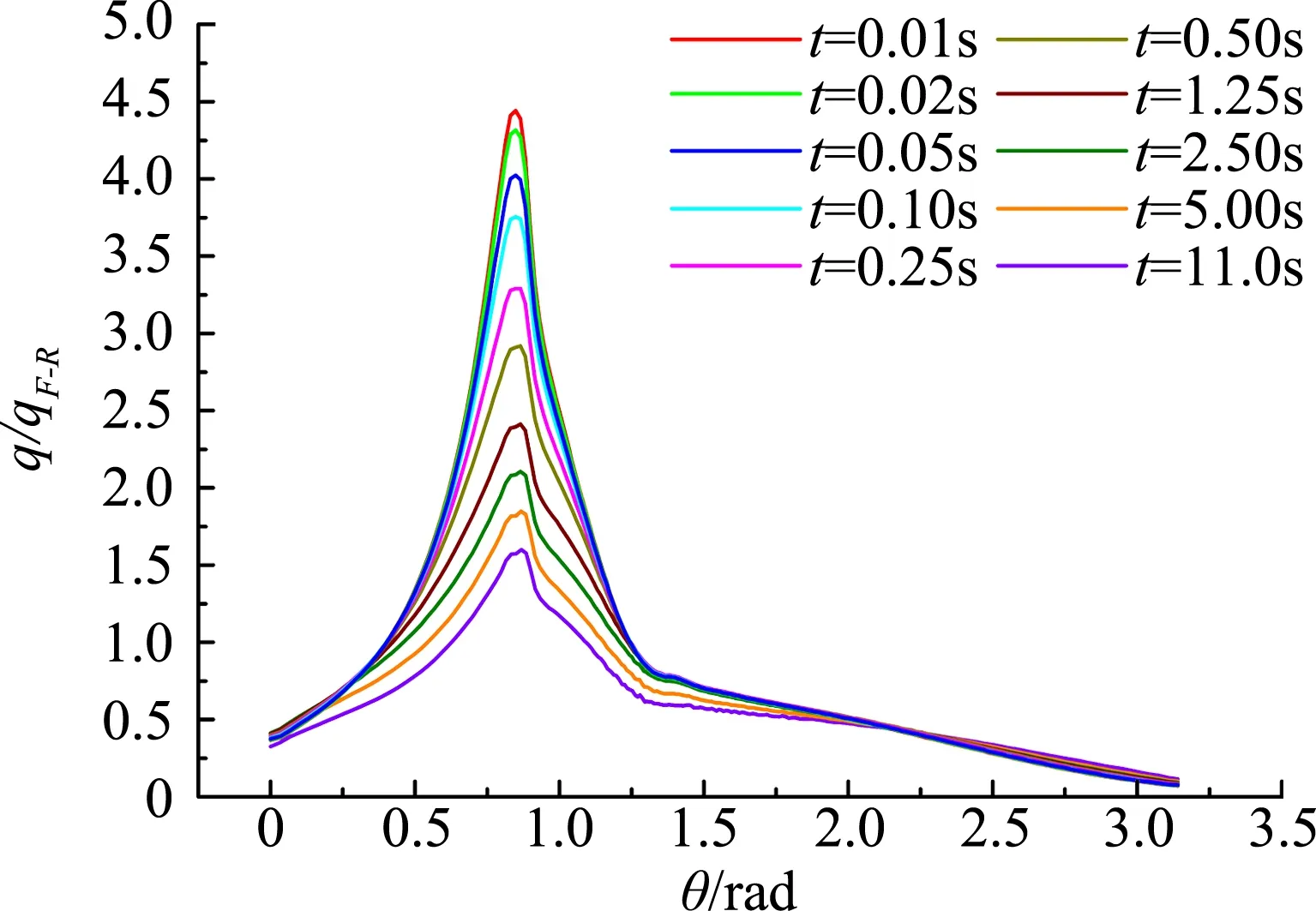
(a) 壁面热流密度

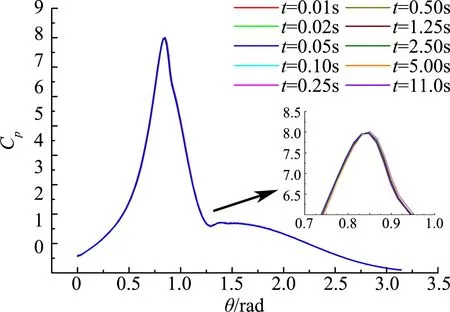
(b) 壁面压力系数图9 进气道前缘壁面热流密度和压力系数随时间演化历程Fig.9 Time history of wall heat flux and pressure coefficient of the leading edge

图10所示为进气道前缘内部结构温度分布和应力分布随时间的演化历程。从图10中可以直观地看出，在高热流撞击作用下，热量首先在撞击区域附近的结构内部迅速累积，致使该处的结构温度迅速升高。随着时间的持续，热量不断累积，逐渐向结构内部纵深区域传递；结构温度也在不断升高，逐渐向结构内部纵深区域不断延展。而且，激波相互作用撞击区域附近的结构内部出现应力集中，随着时间的持续也逐渐向结构内部纵深区域延展。

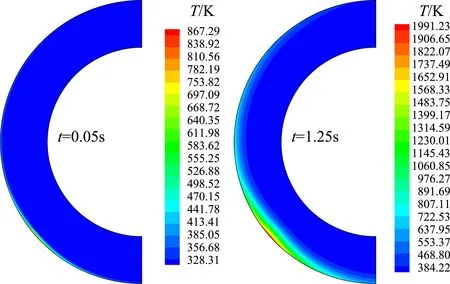
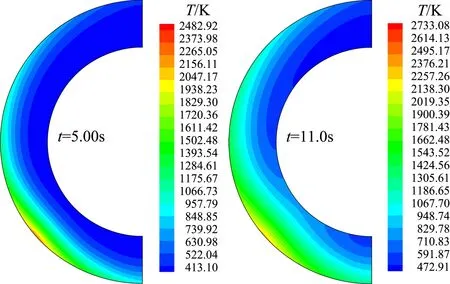
(a) 结构温度分布

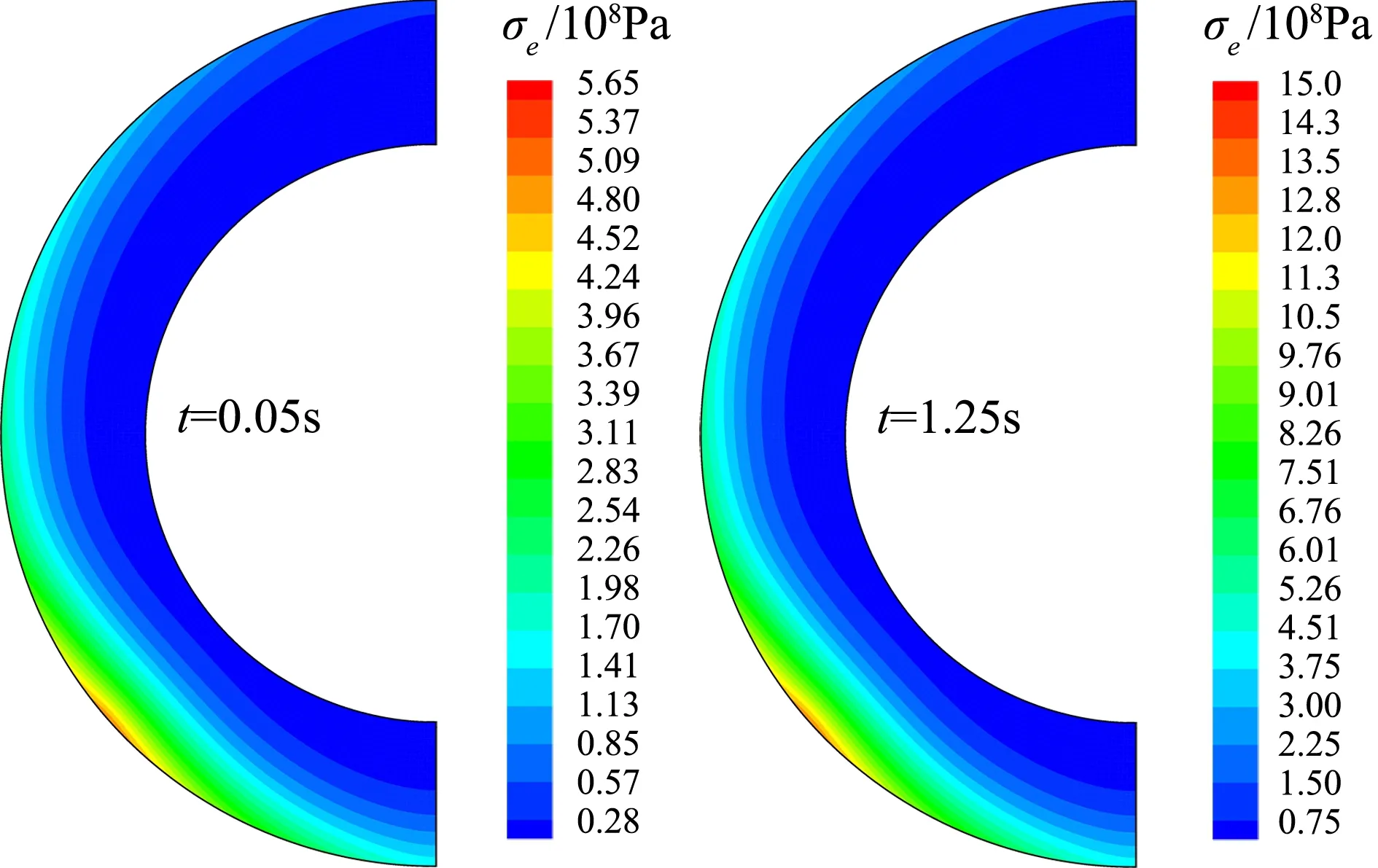
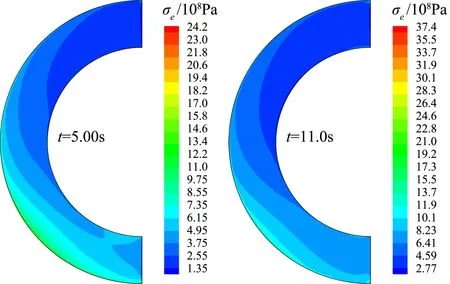
(b) 结构应力分布图10 进气道前缘内部结构温度和应力分布随时间演化历程Fig.10 Time history of structural temperature and stress distribution within the leading edge

综上分析，由于激波相互作用，进气道前缘将遭受强烈的气动力/气动热载荷冲击，在实际飞行过程中即使作用时间很短，也足以造成热防护结构的热学和力学破坏，使其热防护选材和结构设计面临严峻挑战。而且，高超声速飞行器绕流流场普遍存在激波相互作用现象，这些部位将会更长时间地遭受激波相互作用的冲击，因而其热防护也同样会变得更为严峻。

4 结 论

在高超声速流场-热-结构耦合分析平台HyCCD基础上，针对高超声速飞行器进气道前缘进行了初步分析。从中可以发现：激波相互作用使壁面压力系数增大约8倍，而使壁面热流密度增大约5倍。随着时间的持续，流-固之间传热的耦合性使壁面最终达到热平衡状态，而热量逐渐向结构内部纵深区域传递；壁面变形量逐渐增大，在壁面变形量最大区域，压力开始有所增大。在高热流撞击作用下，撞击区域附近的结构温度迅速升高，集中应力逐渐向结构内部纵深区域不断延展。这些规律的认识和分析表明本文发展的HyCCD平台有效地预测了持续长时间飞行条件下的热/力耦合响应时空分布特征和规律，可以用来分析更为真实复杂结构的高超声速流场-热-结构耦合问题，从而为热防护结构的热学/力学综合性能评估以及进一步完善防热结构设计提供理论依据和分析工具。

[1]Thornton E A, Dechaumphai P.Coupled flow, thermal, and structural analysis of aerodynamically heated panels[J].Journal of Aircraft, 1988, 25(11): 1052-1059.

[2]Wieting A R, Dechaumphai P, Bey K S, et al.Application of integrated fluid-thermal-structural analysis methods[J].Thin- Walled Structures, 1988, 11(1-2): 1-23.

[3]Dechaumphai P, Wieting A R, Thornton E A.Flow-thermal-structural study of aerodynamically heated leading edges[J].Journal of Spacecraft and Rockets, 1989, 26 (4): 201-209.

[4]Hassan B, Kuntz D, Salguero D, et al.A coupled fluid/ thermal/flight dynamics approach for predicting hypersonic vehicle performance[R].AIAA 2001-2903, 2001.

[5]Kuntz D W, Hassan B, Potter D L.Predictions of ablating hypersonic vehicles using an iterative coupled fluid/thermal approach[J].Journal of Thermophysics and Heat Transfer, 2001, 15(2): 129-139.

[6]Tran H, Farhat C.An integrated platform for the simulation of fluid-structure-thermal interaction problems[R].AIAA 2002-1307, 2002.

[7]Ferrero P, D′Ambrosio D.A numerical method for conjugate heat transfer problems in hypersonic flows[R].AIAA 2008-4247, 2008.

[8]Bova S W, Howard M A.Coupling strategies for high-speed aeroheating problems[R].AIAA 2011-132, 2011.

[9]Miller B A, Crowell A R, McNamara J J.Loosely coupled time-marching of fluid-thermal-structural interactions[R].AIAA 2013-1666, 2013.

[10]Miller B A, McNamara J J.Efficient time-marching of fluid-thermal-structural interactions[R].AIAA 2014-0337, 2014.

[11]Huang T, Mao G L, Jiang G Q, et al.Two dimensional coupled flow-thermal-structural numerical simulation[J].Acta Aerodynamica Sinica, 2000, 18(1): 115- 119.(in Chinese)黄唐, 毛国良, 姜贵庆, 等.二维流场、热、结构一体化数值模拟[J].空气动力学学报, 2000, 18(1): 115-119.

[12]Gui Y W, Yuan X J.Numerical simulation on the coupling phenomena of aerodynamic heating with thermal response in the region of the leading edge[J].Journal of Engineering Thermo Physics, 2002, 23(6): 733-735.(in Chinese)桂业伟, 袁湘江.类前缘防热层流场与热响应耦合计算研究[J].工程热物理学报, 2002, 23(6): 733-735.

[13]Geng X R, Zhang H X, Shen Q.Study on an integrated algorithm for the flow-fields of high speed vehicles and the heat transfer in solid structures[J].Acta Aerodynamica Sinica, 2002, 20(4): 422-427.(in Chinese)耿湘人, 张涵信, 沈清, 等.高速飞行器流场和固体结构温度场一体化计算新方法的初步研究[J].空气动力学学报, 2002, 20(4): 422-427.

[14]Huang C S, Wu J, Fan H T.Coupled numerical simulation of supersonic flow field and heated structure of flying vehicles[J].Mechanics in Engineering, 2004, 26(2): 24-26.(in Chinese)黄春生, 吴杰, 范绪箕.飞行器流场与结构温度场耦合数值分析[J].力学与实践, 2004, 26(2): 24-26.

[15]Li P F, Wu S P.Numerical simulation of fluid-solid-thermal interaction in hypersonic flows[J].Journal of Aerospace Power, 2010, 25(8): 1705-1710.(in Chinese)李鹏飞, 吴颂平.类航天飞机前身结构与高超声速流场的耦合传热模拟分析[J].航空动力学报, 2010, 25(8): 1705-1710.

[16]Zhang B, Han J L.Multi-field coupled computing platform and thermal transfer of hypersonic thermal protection structures[J].Acta Aeronautica et Astronautica Sinica, 2011, 32(3): 400-409.(in Chinese)张兵, 韩景龙.多场耦合计算平台与高超声速热防护结构传热问题研究[J].航空学报, 2011, 32(3): 400-409.

[17]Li X, Zhang J F, He Y L, et al.Numerical analysis of two-dimensional fluid/thermal structure loosely-coupled simulation[J].Journal of Engineering Thermophysics, 2012, 33(1): 87-90.(in Chinese)李欣, 张剑飞, 何雅玲, 等.二维流场、热结构松耦合模拟研究[J].工程热物理学报, 2012, 33(1): 87-90.

[18]Nie T, Liu W Q.Study of coupled fluid and solid for a hypersonic leading edge[J].Acta Phys.Sin., 2012, 61(18): 184401-1-184401-7.(in Chinese)聂涛, 刘伟强.高超声速飞行器前缘流固耦合计算方法研究[J].物理学报, 2012, 61(18): 184401-1-184401-7.

[19]Zhang S T, Chen F, Liu H.Multi-field coupling numerical analysis approach for aerothermal environment of hypersonic vehicles[J].Acta Aerodynamica Sinica, 2014, 32(6): 861-867.(in Chinese)张胜涛, 陈方, 刘洪.基于多场耦合的飞行器热环境数值分析方法研究[J].空气动力学学报, 2014, 32(6): 861-867.

[20]Zhang S T, Chen F, Liu H.Time-adaptive, loosely coupled strategy for conjugate heat transfer problems in hypersonic flows[J].Journal of Thermophysics and Heat Transfer, 2014, 28(4): 635-646.

[21]Valli A M, Carey G F, Coutinho A L.Control strategies for timestep selection in finite element simulation of incompressible flows and coupled reaction-convection- diffusion processes[J].International Journal for Numerical Methods in Fluids, 2005, 47(3): 201-231.

[22]Zhang S T, Chen F, Liu H.Integrated fluid-thermal- structural analysis for predicting aerothermal environment of hypersonic vehicles[R].AIAA 2014-1394, 2014.

[23]Chen X H, Chen F, Zhang S T, et al.The effects of chemical nonequilibrium and surface catalyticity on aero-thermodynamic characteristics of Hypersonic Vehicles[R].AIAA paper 2016-1252, 2016.

[24]Witteveen J, Bijl H.Explicit mesh deformation using inverse distance weighting interpolation[R].AIAA 2009-3996, 2009.

[25]Mühlenstädt T, Kuhnt S.Kernel interpolation[J].Computational Statistics and Data Analysis, 2011, 55(11): 2962-2974.

[26]Witteveen J.Explicit and robust inverse distance weighting mesh deformation for CFD[R].AIAA 2010-165, 2010.

Fluid-thermal-structural coupling analysis on leading edge of hypersonic inlets

ZHANG Shengtao1,2, CHEN Fang1,*, LIU Hong1

(1.ShanghaiJiaoTongUniversity,Shanghai200240,China;2.AECCCommercialAircraftEngineCO.,LTD,Shanghai200241,China)

By analyzing the mechanism of hypersonic fluid-thermal-structural coupling problem, a multi-field coupling model was described mathematically and physically, and a loose coupling analysis strategy framework was developed.On the basis of this framework, a multi-field coupling analysis platform was realized by using adaptive coupling step-size, hybrid interpolation strategy, and mesh deformation method for complex configuration.A preliminary analysis was conducted on the coupling characteristics of the leading edge of hypersonic vehicle inlets.The calculated results reveal the temporal-spatial characteristics of the fluid-thermal-structural coupling problem in long-time aeroheating environments, and provide theoretical and technical support for the comprehensive performance evaluation and optimization of the thermal protection system of hypersonic vehicles.

hypersonic flow; inlet; fluid-thermal-structural coupling; thermal protection; adaptive coupling step-size; coupling strategy; shock interaction

0258-1825(2017)03-0436-08

2017-02-21;

2017-04-20

国家自然科学基金项目(11102111,11672183,91641129)

张胜涛(1983-),男，山东聊城人，工程师，博士，研究方向：气动热力学及多物理场耦合.E-mail: zhangst9656@163.com

陈方*(1977-)，男，安徽安庆人，副研究员，博士，研究方向：多物理场耦合与燃烧.E-mail：fangchen@sjtu.edu.cn

张胜涛, 陈方, 刘洪.高超声速进气道前缘流场-热-结构耦合分析[J].空气动力学学报, 2017, 35(3): 436-443.

10.7638/kqdlxxb-2017.0036 ZHANG S T, CHEN F, LIU H.Fluid-thermal-structural coupling analysis on leading edge of hypersonic inlets[J].Acta Aerodynamica Sinica, 2017, 35(3): 436-443.

V434+.1

A doi: 10.7638/kqdlxxb-2017.0036