栅格翼大缩比模型超声速风洞试验方法研究

魏忠武, 秦永明,*, 杨学军, 张 江, 欧 平

(1.中国航天空气动力技术研究院, 北京 100074; 2.中国运载火箭技术研究院, 北京 100076)



栅格翼大缩比模型超声速风洞试验方法研究

魏忠武1, 秦永明1,*, 杨学军2, 张 江1, 欧 平1

(1.中国航天空气动力技术研究院, 北京 100074; 2.中国运载火箭技术研究院, 北京 100076)

栅格翼大缩比模型在进行超声速风洞试验时，由于缩比模型的格栅厚度较小、格栅间距较小等问题使得模型加工困难，同时模型结构强度难以满足超声速风洞试验要求，风洞试验中无法真实模拟栅格翼模型的气动特性和飞行器的静稳定特性。针对该问题，基于超声速线化理论对栅格翼提出等效模拟方法。等效模拟方法是设计栅格翼的等效模型，该等效模型与原栅格翼模型气动特性相同。等效模拟方法处理方式为在保持栅格翼外轮廓尺寸及栅格四边之间几何角度不变情况下，按比例系数k减少栅格数，栅格间距增加k倍；保证栅格翼的格宽比不变，将栅格翼弦长增加k倍；保证栅格翼的相对厚度不变，栅格翼筋板厚度增加k倍；等效模型和实际模型纵向压心位置需保持不变。以等效模型和实际模型进行了超声速风洞对比试验，试验结果表明：等效模型和实际模型升力一致，阻力大致相同；飞行器等效模型的静稳定特性和实际模型的静稳定特性相同；栅格翼阻力对飞行器质心所产生的俯仰力矩较升力对飞行器质心所产生的俯仰力矩是小量，栅格翼等效模型在阻力上的微小差异对飞行器的静稳定性影响不大。等效模拟方法可以较好地模拟栅格翼的气动特性和飞行器的静稳定特性，同时解决了大比例缩比所遇到的加工问题和结构强度问题。

栅格翼；等效模拟；大缩比模型；超声速流动；风洞试验

0 引 言

作为气动稳定面、控制面的栅格翼，是一种由众多薄的栅格壁镶嵌在边框内、具有型面的或平面的板条组成的受力空间系统，拥有空间分布的自由涡系的升力面系统和多翼面系统的两个基本特征。它是一种新型的承力稳定面和控制面，较之单翼面有许多优点：(1) 在规定刚度的情形下质量小，方便折叠，可以使弹翼折叠在弹身上，特别适用于管式发射、机载悬挂，也便于这类导弹的结构设计，而且承力部件比较分散，更容易设计成最大刚度面与最大气动载荷作用面相重合，从而减轻翼面重量；(2) 在体积比较小的情况下，可以得到比较大的受力面积，具有大的升力，不大的铰链力矩，并避免飞行过程中飞行器压心的大幅度偏移。前苏联的试验表面，在体积相等时，栅格翼的升力要比单翼面的大好几倍，如M∞=4.0时大三倍。(3)栅格翼失速攻角大并且升力特性好，特别适合作为导弹的全动舵面，可以采用较小功率的舵机，使导弹产生更大的法向过载，利于导弹的控制；栅格翼还有其它的一些结构和气动特点。鉴于栅格翼独特优越性，而得以在飞行器工程研究应用，如俄罗斯“联盟”号飞船逃逸救生系统的稳定翼面，俄罗斯R-77、AAM-AE空空导弹的控制舵面，中国CZ-2F火箭有效载荷级的飞船逃逸救生系统的稳定翼面，印度SLCM潜射巡航导弹的控制舵面等[1-6]。

大缩比栅格翼模型在进行超声速风洞试验时，由于栅格翼载荷大、栅格壁薄等问题，如果取与弹身相同的缩比，即按完全几何相似的缩比设计带栅格翼的风洞试验模型，往往会遇到以下几个方面的问题：

(1) 缩比后栅格壁的厚度很小，有的甚至小于0.1 mm，给模型加工带来很多困难，甚至在加工工艺上很难实现；

(2) 由于载荷大，缩比后栅格翼的强度和刚度都很弱，基本上无法满足高速暂冲式风洞试验的要求，模型在高速气流中很容易被破坏，特别是风洞启动时气流对模型的冲击引起栅格翼的损坏，造成试验失败；

(3) 模型缩比后，边界层效应和实际模型有所差别造成气动特性模拟失真，甚至由于栅格间间距很小，造成气流的堵塞，无法真正模拟飞行器的气动特性。

苏、美等国家在进行栅格翼模型试验研究时，可以在大型超声速风洞(4 m量级以上)中进行全尺寸缩比模型试验研究，在一定条件下，也可通过特殊装置进行实际尺寸栅格翼的单独试验研究。而国内超声速风洞特征尺寸相对要小，对于一些栅格翼飞行器无法做到全尺寸模型的风洞试验，国内也尚没有栅格翼飞行器大比例缩比模型高速风洞试验的成熟方法。故本文基于等效模拟思想，研究带栅格翼飞行器大缩比模型在超声速风洞条件下的静稳定特性的试验模拟方法。

1 等效模拟方法

由于栅格翼独特的气动特性，栅格翼应用于飞行器上时，考虑到飞行器的静稳定特性，栅格翼作为控制舵面一般安装于飞行器的尾部。风洞试验在进行带栅格翼飞行器静稳定特性试验时，由于栅格翼大缩比所具有的困难，需要对栅格翼进行等效处理，要求等效处理前后的飞行器静稳定特性相同。

当栅格翼相邻栅格之间不发生相互干扰时，栅格翼的栅格和边框均可以看做是二维的薄翼，栅格翼的升力为各薄翼升力的合力，阻力为各薄翼阻力的合力及栅格节点产生的阻力。在本次研究试验状态中，栅格节点产生的阻力相对较小，研究中将其作为次要因素不做考虑。在超声速线化理论中，薄翼的升力系数和零升波阻系数可由下式给出：

(1)

(2)

由式(1)和式(2)可以看出，薄翼型的升力系数只与攻角和来流马赫数有关，也就是在相同攻角、相同来流马赫数、相同翼面积时，无干扰薄翼的升力相同。对于无弯度对称翼型，零升波阻系数与翼型几何形状、来流马赫数和翼型相对厚度有关，在保证翼型几何形状和相对厚度不变的情况下，相同来流马赫数时，薄翼的零升波阻相同[7-8]。

在栅格翼大缩比模型超声速试验时，栅格翼的等效模型可以按照如下方式进行处理。为了满足缩比模型的加工工艺和强度要求，将栅格数按一定比例减少，增加栅格间距，但需要保持栅格翼外轮廓尺寸不变，同时保持栅格四边之间角度不变；在减小栅格数的同时，按比例增加栅格翼弦长，保证栅格翼的翼面积不变；在减小栅格数的同时，按比例增加栅格翼筋板厚度，保证栅格翼的相对厚度不变。由于栅格翼的格栅几何形状和翼面积相同，可以保证栅格翼的升力相同；栅格翼筋板厚度的增加产生的压强对翼弦是上下对称的，所以厚度对升力和力矩都无贡献，即栅格翼的力矩也不会发生变化；栅格翼筋板厚度增加，但其相对厚度没有发生变化，故其零升波阻相同，在超声速时栅格翼的零升阻力主要是波阻，所以栅格翼的零升阻力变化也不大。栅格翼对飞行器静稳定性影响量是由栅格翼受到的气动力对飞行器质心的俯仰力矩来体现的，由于栅格翼距飞行器质心较远，栅格翼升力对质心所产生的俯仰力矩较阻力对质心所产生的俯仰力矩大得多，所以栅格翼等效模型在阻力上的微小差异对飞行器的静稳定性影响不大。

栅格翼既可作为稳定面，又可作为控制面，对大多数战术武器来说是稳定面和控制面兼顾。在等效模型设计时，为保证舵控效率和铰链力矩相同，采取栅格翼压心绝对位置不变方式对栅格翼弦长进行等比例增加。按上述的等效模拟方法，栅格翼的宽度、高度、栅格相对厚度、翼弦格宽比相同，栅格间的流动状态相同，栅格翼气动力对飞行器质心俯仰力矩相同。

2 风洞和模型

2.1 风 洞

试验在中国航天空气动力技术研究院FD-12风洞中进行。风洞为暂冲式亚、跨、超声速风洞，试验段横截面尺寸为1.2 m×1.2 m，超声速试验段的长度为2.4 m，采用更换固块式二元喷管来改变马赫数，马赫数范围为1.5～4.0。在风洞的超扩段里有一套攻角机构，攻角范围为-15°～25°，还可以利用15°弯接头进行大攻角试验，可实现的攻角范围为0°～40°。试验段侧壁两侧各有两个Φ500 mm观察窗，供观察或纹影仪拍摄流场用。

2.2 模 型

栅格翼模型采用斜格蜂窝状栅格翼模型，弹体头部为卡门曲线，Rm/L=0.2，Rm为弹体头部底截面半径，L为弹体头部长度。栅格翼距弹体头部距离为16Rm。试验中根据等效模拟方式不同而栅格翼模型不同，同时模型缩比不同时栅格翼和弹体为等比例缩比模型。

飞行器上安装栅格翼作为控制舵面，栅格翼一般为多个，环飞行器尾部且纵向对称布置。本文研究飞行器上安装栅格翼的数目为8个，且沿飞行器尾部周向均布，成“米”字型。考虑栅格翼在加工上比较复杂，所以只对单个栅格翼模型进行设计和风洞试验，对称状态按照状态相同的结果进行对称处理。

图1为栅格翼模型在风洞中照片。图2为试验模型栅格翼部件图。图3为栅格翼风洞试验纹影照片。图4为栅格翼与弹体相对位置示意图。试验的栅格翼模型基本参数见表1。

图1 栅格翼风洞试验模型Fig.1 Grid fin model in the wind tunnel

图2 栅格翼测力试验部件Fig.2 Model of grid fin parts

图3 栅格翼风洞试验纹影照片Fig.3 Schlieren image of the test

(a) Φ=0° (b) Φ=45° (c) Φ=90°图4 栅格翼与弹体相对位置示意图(前视)Fig.4 Relative position of grid fin and body表1 栅格翼模型基本参数Table 1 Basic parameter of grid fin models

翼面编号栅格数缩比翼高/mm翼宽/mm弦长b/mm格距t/mm格壁厚度/mm边框厚度/mm翼A16×161∶2304.3030027.5013.281.00.75翼B116×161∶5121.7012011.005.310.40.30翼B212×121∶5121.7012014.677.080.40.30翼B38×81∶5121.7012022.0010.620.40.30翼B44×41∶5121.7012044.0021.250.40.30翼B54×41∶5121.7012044.0021.251.60.60翼C4×41∶1060.856022.0010.620.80.60翼D4×41∶2030.433011.005.310.40.30

2.3 风洞试验方法

试验采用单独测量栅格翼气动力的方法进行研究。弹体和天平分别支撑在专用支杆上，栅格翼与测试天平固连，弹体与栅格翼之间留有适当间隙以保证弹体受到的气动力不会传递到天平上。试验马赫数范围Ma=3.0～4.0，滚转角范围Φ=0°～90°，攻角范围-4°～4°，基于自由流条件的单位长度雷诺数范围23.75×106/m～32.26×106/m。

3 结果和讨论

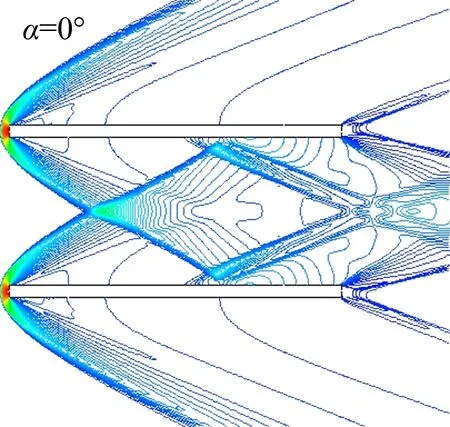
超声速下，栅格翼的零升阻力主要是波阻，波阻由栅格翼上的压力分布积分而得。当栅格翼之间相互影响时，栅格翼上的压力分布规律比较复杂，栅格翼的升阻特性也会受到影响。在超声速下，栅格翼前缘的斜激波有可能对相邻栅格附近的流动产生影响。当来流速度小于第三临界马赫数时，栅格翼前缘斜激波在相邻格壁间相交和反射，格壁之间的流动会相互影响；当来流速度大于第三临界马赫数时，格壁之间的流动不会相互影响[9-16]。对于本文研究的栅格翼，理论外形在马赫数3及以上来流条件下栅格翼前缘激波均不会在栅格之间产生反射。但由于在加工时工艺上无法保证栅格翼前后缘倒角的精度，栅格翼前后缘均未进行倒角处理，因此在超声速时栅格翼前缘不再是附体斜激波，而是脱体激波，激波会在栅格之间产生反射，如下图5。由于等效模型间翼弦格宽比相同，可认为其流态是一致的。

3.1 相同缩比、不同等效模型气动特性

栅格翼模型在缩比为1∶5时，完全缩比模型和不同等效模型在相同缩比下均进行了风洞测力试验，试验马赫数为3.5，栅格翼的升力特性和阻力特性曲线见下图6(Φ=0°)。由于栅格翼模型为钝前缘，此时如果将栅格翼作为是由许多薄直翼的组合进行等效，其阻力特性可能会有一定的差异。本次试验还对栅格翼等效模型间相对厚度不同造成阻力的差异进行了试验研究。

翼B1按栅格翼原型(16格×16格)进行完全缩比，翼B2～B5为不同的等效方式模型，其中翼B2～B4在减小栅格数的同时，按比例增加栅格翼弦长，B5在减小栅格数、按比例增加栅格翼弦长的同时，按比例增加栅格翼筋板厚度。从数据结果可以看出，栅格翼模型在减小栅格数的同时，按比例增加栅格翼弦长可以保证栅格翼的升力面积，等效模型间升力特性一致。其中翼B1和翼B5的升力系数接近，而与翼B2、B3、B4有所差异，主要是由于栅格翼的相对厚度没有完全等效，造成不同翼的栅格间流动状态不同，栅格翼迎风面积及头部激波在相邻栅格上的影响区域不同造成的。从阻力特性上可以很明显看出，相对厚度不同时阻力系数差异较大，相对厚度相同时阻力系数接近。模型设计时，考虑翼B5边框的结构强度相对较弱，于是将其边框的厚度增加了1倍。翼B1和翼B5的相对厚度相同，但翼B1栅格节点数是翼B5的13.3倍，但翼B5阻力较翼B1略大，说明本研究试验状态栅格节点对栅格翼阻力特性影响很小，翼B5阻力较翼B1略大是由于翼B5边框加厚引起的。

本次试验中还对栅格翼与弹体不同位置(Φ=45°和90°)进行了风洞试验研究，其规律与Φ=0°类似。对于全弹模型，弹体为旋成体，栅格翼共8片呈“米”字形布置于弹体尾部附近。与弹体不同位置栅格翼的气动特性可以按照流动一致的状态进行对称处理。8片栅格翼对飞行器质心的俯仰力矩由栅格翼升力和阻力分别对模型质心产生的俯仰力矩组成，栅格翼升(阻)力对模型质心的俯仰力矩由栅格翼升(阻)力及栅格翼气动中心与模型质心相对位置关系求出。图7为通过试验数据进行对称处理与转化得到的结果。

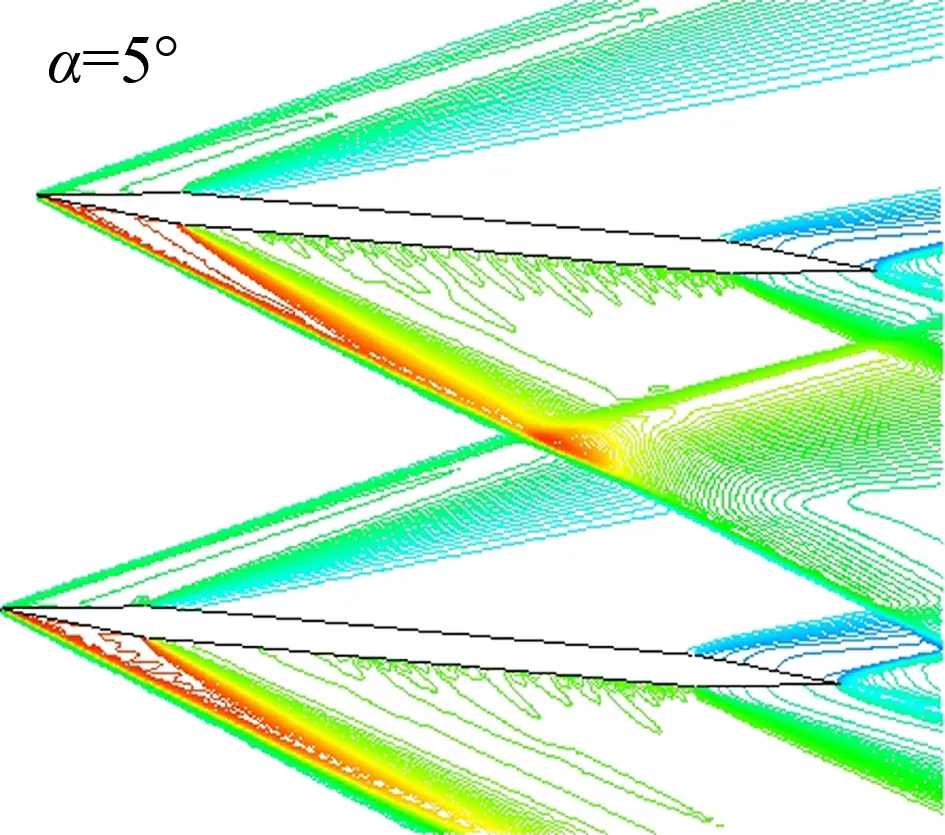
(a) 前后缘均有倒角

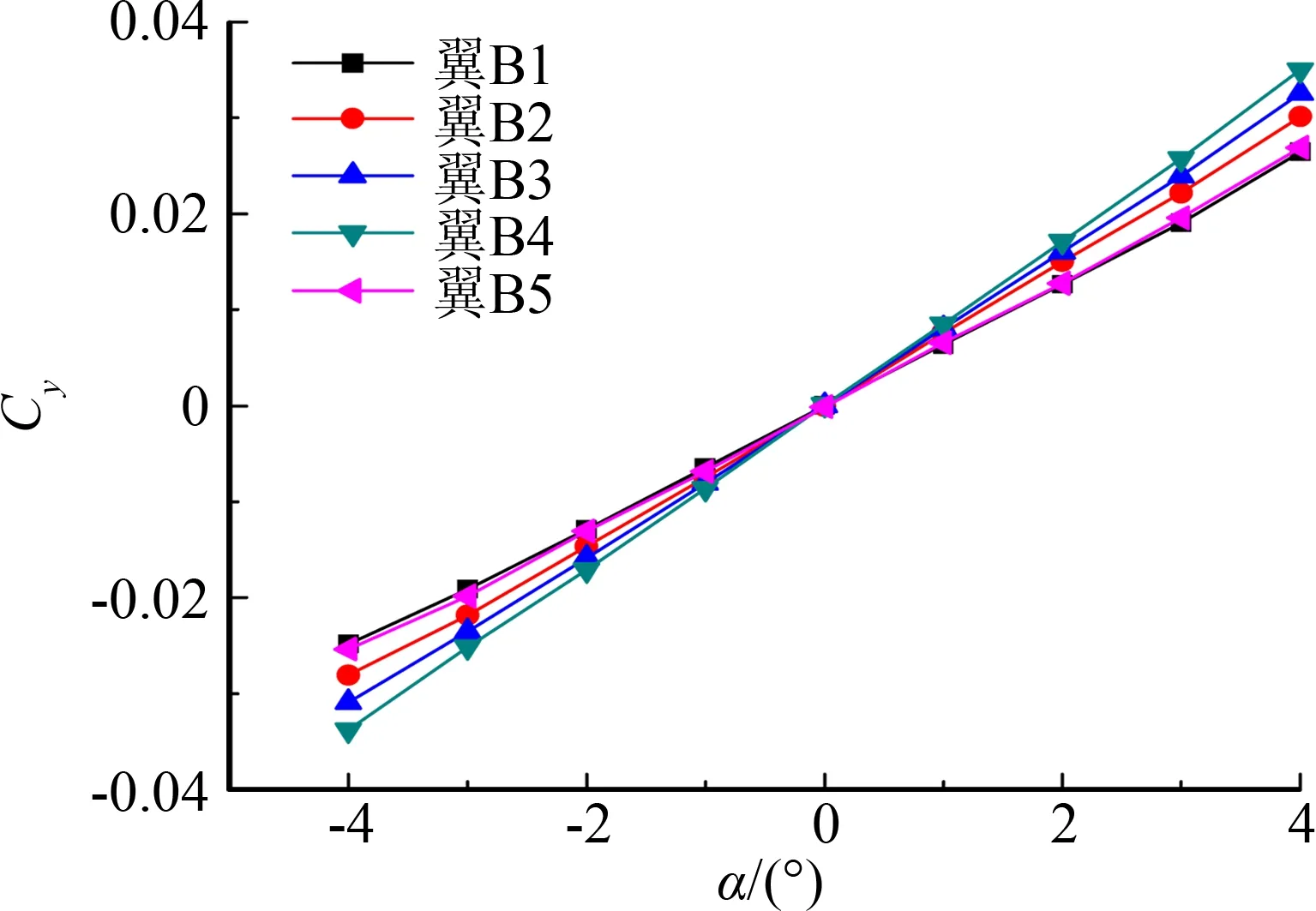
(a) 升力系数随攻角变化曲线

(b) 阻力系数随攻角变化曲线图6 栅格翼不同等效模型气动特性曲线Fig.6 Aerodynamic characteristics of different equivalent simulation methods

从图中可以看到，由于升力对飞行器质心的力臂较阻力对飞行器质心的力臂大，升力引起的俯仰力矩较阻力引起的俯仰力矩大得多，如此升力的差异会引起对质心俯仰力矩明显的差异，而阻力的差异对质心俯仰力矩引起的差异很小。因而为了更好地模拟飞行器的静稳定性，要求栅格翼等效模型和实际模型之间的升力完全一致，阻力大致相同。

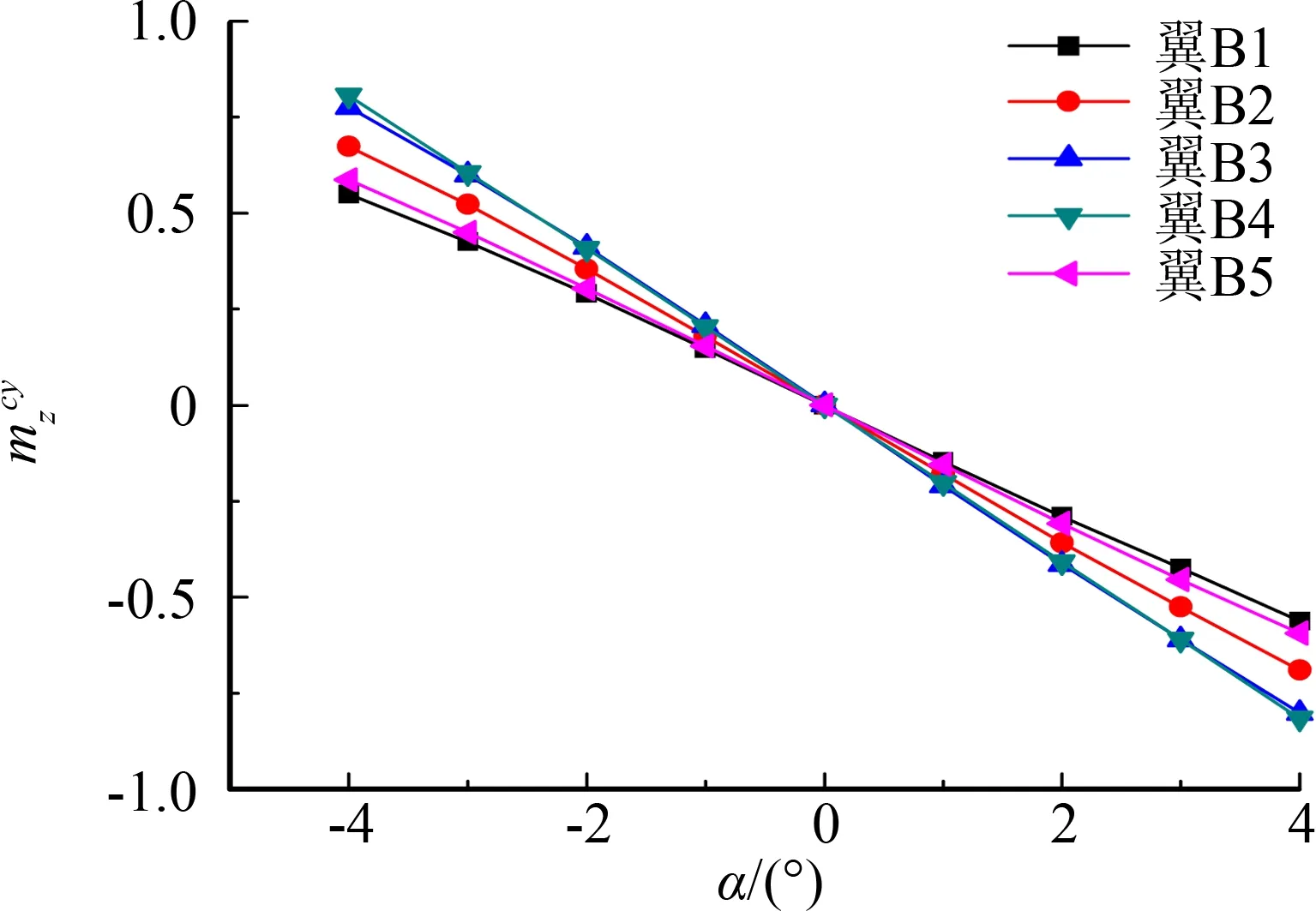
(a) 升力对飞行器质心的俯仰力矩

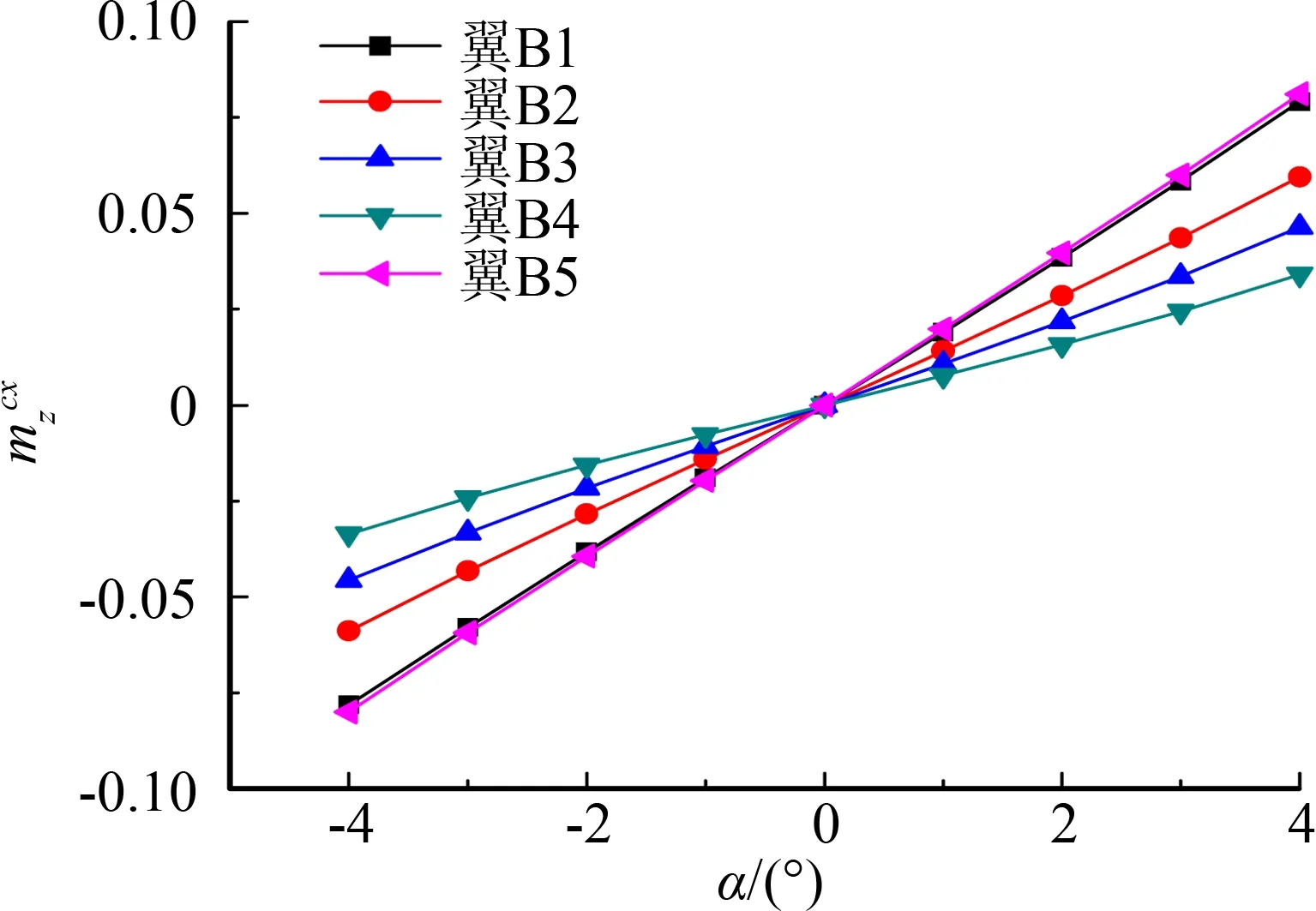
(b) 阻力对飞行器质心的俯仰力矩图7 栅格翼对飞行器质心俯仰力矩特性曲线Fig.7 Aerodynamic characteristics of pitching moment

从以上结果可以得到：相同缩比下，减小栅格数需按比例增加栅格翼弦长保证栅格翼翼面积不变，同时按比例增加栅格翼筋板厚度保证格栅相对厚度不变，等效模型和实际模型的升力、阻力特性一致，而且飞行器的静稳定性相同。

3.2 不同缩比、不同等效模型气动特性

从3.1节中可以确定在相同缩比状态下，按照翼面积相等、格栅相对厚度相等的等效缩比模型的气动特性和实际模型完全缩比的气动特性一致。下面研究不同缩比状态下，栅格翼完全缩比和等效缩比模型气动特性的差异。试验结果见图8。其中翼A为实际模型完全缩比模型，缩比为1∶2；翼B1为实际模型完全缩比模型，缩比为1∶5；翼B5为等效缩比模型，缩比为1∶5；翼C为等效缩比模型，缩比为1∶10；翼D为等效缩比模型，缩比为1∶20。

从图8、图9可以看出，不同缩比，按照等效方法给出的等效模型，升力特性具有较好的一致性。阻力上表现的差异性主要是由于在进行等效缩比模型时，栅格翼的边框较薄，加工难度大，且强度较弱，无法满足风洞试验要求，遂对栅格翼边框进行一定的加厚处理，同时栅格翼为钝前缘，如此造成栅格翼边框的迎风面积增加，带来波阻的增加。

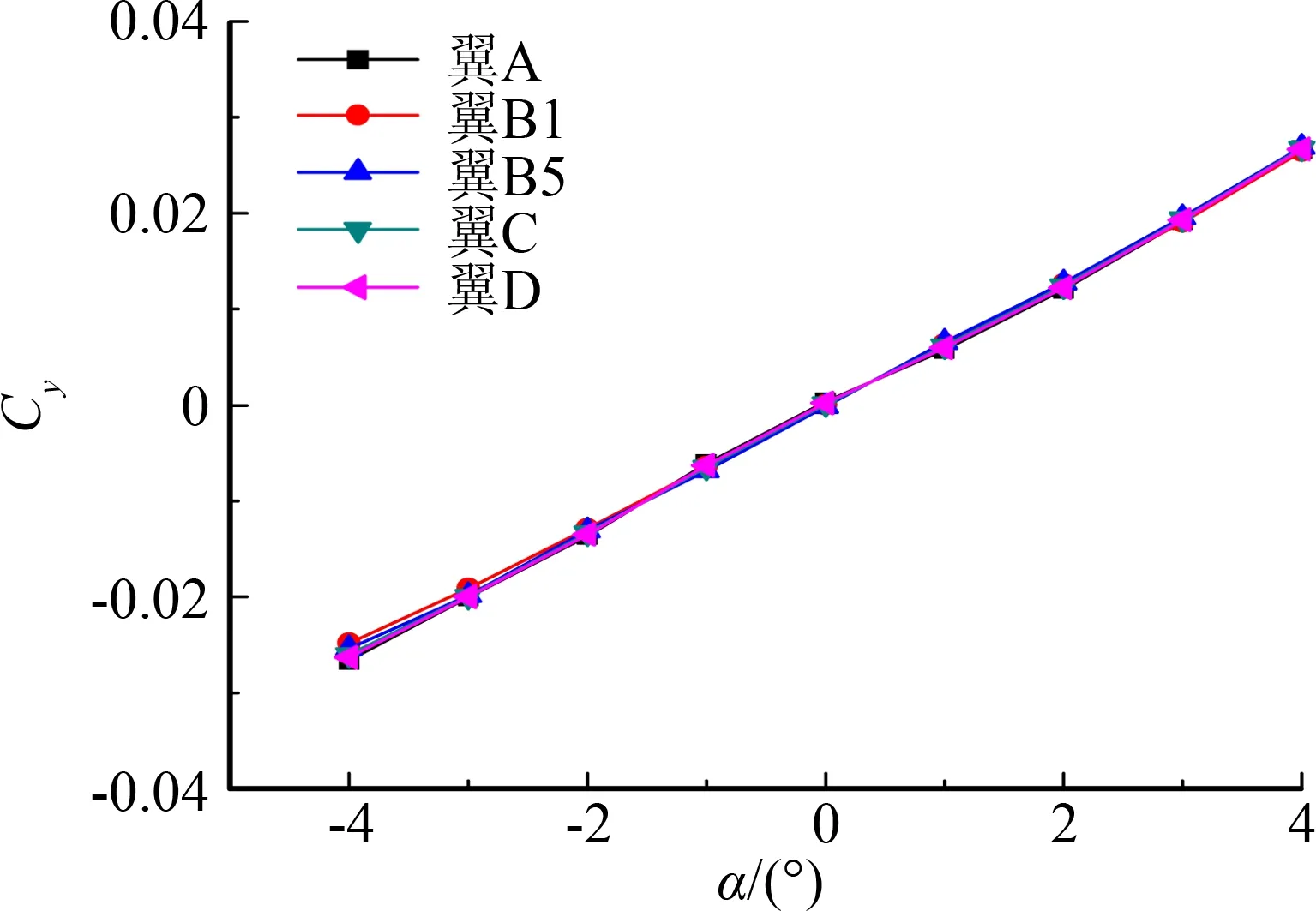
(a) 升力系数随攻角变化曲线

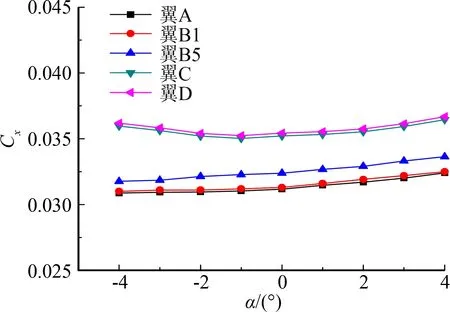
(b) 阻力系数随攻角变化曲线图8 同缩比、不同等效模型气动特性曲线Fig.8 Aerodynamic characteristics of different methods

(a) 升力对飞行器质心的俯仰力矩

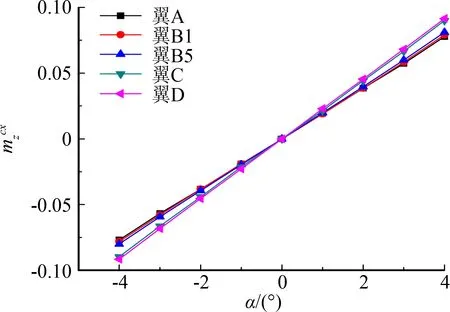
(b) 阻力对飞行器质心的俯仰力矩图9 栅格翼对飞行器质心俯仰力矩特性曲线Fig.9 Aerodynamic characteristics of pitching moment

从以上结果可以看出，栅格翼模型在不同缩比、不同等效模型时：升力特性一致，阻力特性相当；栅格翼对飞行器质心的俯仰力矩完全一致；相同缩比后，飞行器等效模型和实际模型的静稳定特性相同。

4 结 论

1) 栅格翼在大缩比尺寸超声速风洞试验时，可以采用在保证栅格几何形状、翼面积、相对厚度、翼弦格宽比不变情况下得到等效的模型外形，等效外形和实际外形的常规气动特性一致。本文提出的等效方法可以对栅格翼模型常规气动特性进行模拟，同时可以解决大比例缩比所遇到的加工和强度难以保证的现实问题。

2) 栅格翼升力对飞行器质心所产生的俯仰力矩较阻力对飞行器质心所产生的俯仰力矩大得多，栅格翼等效模型在阻力上的微小差异对飞行器的静稳定性影响不大。

3) 在栅格翼等效模型和实际模型之间的升力完全一致、阻力大致相同时，飞行器等效模型的静稳定特性和实际模型的静稳定特性相同。

[1]Guo J T, Lu F L, Wang K, et al.Current status and development trend on the aerodynamics characteristic of grid fin[J].Journal of Zhongyuan University of Technology, 2011, 22(6): 47-51.(in Chinese)郭江涛, 陆飞龙, 王柯, 等.栅格翼气动特性研究现状及应用前景[J].中原工学院学报, 2011, 22(6): 47-51.

[2]Washington D W, Miller M S.Grid fins: a new concept for missile stability and control[R].AIAA 1993-35.

[3]Despirito J, Edge H L, Weinacht P, et al.CFD analysis of grid fins for maneuvering missiles[R].AIAA 2000-391.

[4]Lu Z R, Shen X L, Tong Z L, et al.Calculation and analysis of grid fin configurations [J].Journal of Bejing University of Aeronautics and Astronautics, 1996, (5): 575-580.(in Chinese)陆中荣, 沈遐龄, 童自力, 等.栅格翼空气动力特性的计算与分析[J].北京航空航天大学学报, 1996, (5): 575-580.

[5]Yang X H, Wang C Y.Calculation of aerodynamic forces on the vehicle and grid fins in the complex three-dimensional fluid field[J].Journal of National University of Defense Technology, 1996, (3): 1-4.(in Chinese)杨晓辉, 王承尧.飞行器栅格翼三维复杂流场的气动力计算[J].国防科技大学学报, 1996, (3): 1-4.

[6]Ren H Y, Cai Y, Sun H S.Study on aerothermodynamics of hypersonic grid fin[J].Journal of Astronautics, 2010, (1): 44-49.(in Chinese)任怀宇, 蔡昱, 孙洪森.高超声速栅格翼气动特性研究[J].宇航学报, 2010, (1): 44-49.

[7]徐敏, 安效民.飞行器空气动力特性分析与计算方法[M].西安: 西北工业大学出版社, 2012.

[8]C M 贝洛奇尔科夫斯基, 等, 著.栅格翼[M].王丹阳, 等, 译.北京: 中国运载火箭技术研究院, 1994.

[9]Chen S S, Zhang J Y.Influence ofwidth to chord ratio on aerodynamics characteristic of grid fins[J].Journal of Nanjing University of Science and Technology, 2005, (12): 693-696.(in Chinese)陈少松, 张建叶.格宽翼弦比对栅格翼气动特性的影响[J].南京理工大学学报, 2005, (12): 693-696.

[10]Zhang L, Wang S H, Jiang G Q.Influence of blunt leading edge on shock-shock interaction and heat flux distribution of grid fin[J].Journal of Astronautics, 2010, (2): 324-328.(in Chinese)张亮, 王淑华, 姜贵庆.钝化前缘对栅格翼激波干扰与热流分布的影响[J].宇航学报, 2010, (2): 324-328.

[11]Lu Z R, Wang H W.Experimental studies of the characteristics of the flow about a grid fin[J].Experiments and Measurements in Fluid Mechanics, 2002, 16(1): 21-26.(in Chinese)陆中荣, 王海文.栅格翼绕流特性的实验研究[J].流体力学实验与测量, 2002, 16(1): 21-26.

[12]Chen S S, Xu Q, Wang F H, et al.The research of drag

reduction characteristics of grid fins[J].Experiments and Measurements in Fluid Mechanics, 2001, (4): 7-11.(in Chinese)陈少松, 徐琴, 王福华, 等.栅格翼减阻特性研究[J].流体力学实验与测量, 2001, (4): 7-11.

[13]Chen S S, Xu Q, Wang F H, et al.Aerodynamic analysis of grid fin configurations at supersonic speed[J].Journal of Ballistics, 2000, 12(2): 50-54.陈少松, 徐琴, 王福华, 等.栅格翼组合体的超音速气动特性研究[J].弹道学报, 2000, 12(2): 50-54.

[14]John E B.Grid fins for missile applications in supersonic flow[R].AIAA 96-0194, 1996.

[15]Washington W D, Booth Pamela F, Miller M S.Curvature and leading edge sweep back effects on grid fin aerodynamic[R].AIAA 1993-3480.

[16]Wu J S, Lei J M.Aerodynamic configuration and characteristic of guided weapons[M].Beijing: National Defend Industry Press, 2008.吴甲生, 雷娟棉.制导兵器气动布局与气动特性[M].北京: 国防工业出版社, 2008.

Investigation of grid fins on large-scale model test in supersonic wind tunnel

WEI Zhongwu1, QIN Yongming1,*, YANG Xuejun2, ZHANG Jiang1, OU Ping1

(1.ChinaAcademyofAerospaceAerodynamics,Beijing100074,China;2.ChinaAcademyofLaunchvehicleTechnology,Beijing100076,China)

Aerodynamic characteristic and static stability of experimental model with grid fins cannot be simulated veritably in supersonic wind tunnel, as that structural strength of the model cannot meet the requirement of supersonic wind tunnel test, and it is difficult to manufacture the model with small grating thickness and small grid spacing.To cope with these problems, this paper offers an equivalent analog method based on supersonic linearized theory.The equivalent analog method is to design an equivalent model with the same aerodynamic characteristic as that of the grid fin model.The specific implementation of the equivalent analog method consists of the following procedures: overall dimensions and geometric angles between four sides of grid fins remain unvaried, while the grid spacing expands byktimes and the amount of the grid reduces byktimes; the grid width ratio maintains its value whereas the chord length enlarges byktimes; relative thickness keeps unchanged though the thickness of ribs increases byktimes; and longitudinal pressure centers of the equivalent and original models are the same.The wind tunnel test of an original model was compared with that of the equivalent model.The lifts in the two tests were identical, and the drags were similar.An identical behavior was observed in the two tests for the aerodynamic characteristics and the static stability.The influence of the drag was insignificant on the centroid and the static stability.The equivalent analog method can present

relatively veritable simulation of aerodynamic characteristics and static stability for grid fins, and solve the problems in manufacturing and structural strength of large-scaled model.

grid fin; equivalent simulation; large-scale model; supersonic flow; wind tunnel test

0258-1825(2017)03-0392-07

2015-02-10;

2015-07-08

魏忠武(1986-)，男，江苏徐州人，工程师，研究方向：试验空气动力学.E-mail：weizhw@126.com

秦永明*(1976-)，男，河北献县人，研究员，主要研究方向：试验空气动力学.E-mail: qymincaaa@sina.com

魏忠武, 秦永明, 杨学军, 等.栅格翼大缩比模型超声速风洞试验方法研究[J].空气动力学学报, 2017, 35(3): 392-398.

10.7638/kqdlxxb-2015.0024 WEI Z W, QIN Y M, YANG X J, et al.Investigation of grid fins on large-scale model test in supersonic wind tunnel[J].Acta Aerodynamica Sinica, 2017, 35(3): 392-398.

V211.71

A doi: 10.7638/kqdlxxb-2015.0024