非对称应力作用下直墙马蹄形隧道塑性区研究

徐 晓 洋

(上海理工大学环境与建筑学院，上海 200093)



非对称应力作用下直墙马蹄形隧道塑性区研究

徐 晓 洋

(上海理工大学环境与建筑学院，上海 200093)

基于已有的圆形洞口围岩塑性区解答，通过旋转极坐标轴角度，由复变函数保角映射方法，得到了非对称应力作用下直墙马蹄形隧道围岩塑性区半径解析公式，并结合算例进行了分析，通过塑性区半径分布图验证了该方法的有效性。

非对称应力，直墙马蹄形隧道，塑性半径，保角变换

0 引言

在隧道工程建设中，隧道在非对称应力作用下的变形对隧道的安全有重要影响。目前，对于非对称应力作用下直墙圆拱马蹄形隧道的塑性区范围的研究资料还不多见。前苏联学者K.B.鲁宾涅特利用弹塑性力学方法推导了圆形洞室的塑性范围解析公式。郭佳奇等[2]基于圆形洞室塑性区解答，通过保角映射函数推导了极坐标下椭圆型洞室塑性区的解答。陈超等[3]通过旋转极坐标轴和保角映射方法，求得在偏压荷载下曲墙马蹄形隧道塑性半径解答。本文基于已有的圆形洞口围岩塑性区解答，按照陈超方法推导了在非对称应力作用下直墙马蹄形隧道围岩塑性区半径解析解，并结合算例进行了分析。

1 塑性区半径计算

为求解非对称应力作用下直墙马蹄形隧道围岩塑性区半径，将计算过程分为两个阶段：第一阶段，在圆形洞室的鲁宾涅特解的基础上，通过旋转主应力的角度，求解出非对称应力作用下圆形洞口的围岩塑性半径公式；第二阶段，通过保角映射函数，将旋转后圆形洞口的塑性区域映射到z平面上直墙圆拱马蹄形隧道的塑性区域。

1.1 非对称应力下圆形洞口围岩塑性半径

根据文献[1]，圆形洞室在ζ平面上单位圆洞口外部的塑性半径表达式为：

(1)

其中，rp为塑性半径;R0为ζ平面上的单位圆半径;θ为极坐标下的极角;ρ为相应角度处弹塑性交界线的坐标极径;λ为岩体侧压力系数(一般λ>1);c为岩体粘聚力;φ为岩体内摩擦角;p为洞室上部垂直地应力。

为了得到非对称应力的情况，将极坐标轴旋转α角度，可得变换后偏压角度θ=θ′-α，将旋转后的偏压角θ代入式(1)替换，即可得到偏压角为α的单位圆洞口外部塑性区半径公式为：

(2)

其中，α为偏压主应力与水平方向的夹角(规定以逆时针为正)，其他参数含义同式(1)。

1.2 非对称应力下马蹄形隧道围岩塑性半径

一般使用映射函数把z平面上的区域转换为ζ平面上单位圆的外域，其最普遍形式展开为洛朗级数如下：

(3)

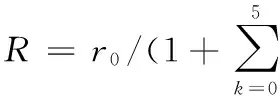
(4)

根据式(4)，可以得到对应的z平面的塑性区半径表达式为：

(5)

其中，参数含义同式(1)～式(4)。

2 算例分析

为对上述方法进行验证，结合以下算例进行分析。隧道几何尺寸：隧道为直墙圆拱，上半圆拱的直径为6.0 m，直墙的高度为6.0 m，模型如图1所示。隧道围岩计算参数如下：弹性模量取6.0 MPa，泊松比取0.25，粘聚力c=3.0 MPa，内摩擦角φ=40°，重度为2 000 kg/m3。围岩受到非对称主应力σ1=30 MPa，σ3=15 MPa，σ1与水平线夹角分别为15°，30°，45°三种工况，侧压力系数λ=2.0。

根据参考文献[4]，取式(3)中洛朗级数前六项，映射系数Ck的值分别为：C0=-0.103 6，C1=0.087 3，C2=0.072 9，C3=-0.098 4，C4=0.038 4，C5=-0.005 2，并计算得出反映孔形的系数R=3.294 m(其中，r0取3.0 m)。

将以上系数代入式(3)，求得映射函数为：

(6)

代入式(4)，得出实部与虚部为：

(7)

将隧道的相关参数代入式(2)得出：

ρ′=1.53[1-0.722cos(2(θ-α))]

(8)

其中，α为偏转角度。

联立式(5)，式(7)，式(8)即可求出塑性半径r的表达式，根据所给的计算参数和几何参数可以绘制不同偏转角下的塑性区域分布图，如图2所示。

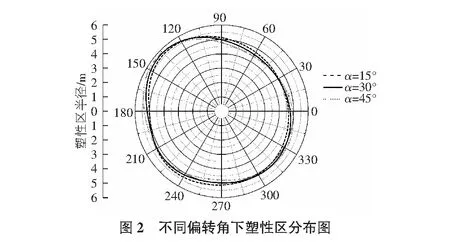
3 结语

基于已有的圆形洞口围岩塑性区解答，通过旋转极坐标轴角度，再利用复变函数保角映射方法，推导了在非对称应力作用下直墙圆拱马蹄形隧道围岩塑性区半径解析解，并绘制了不同偏压角度下的塑性区半径分布图。

[1] 蔡美峰.岩石力学与工程[M].北京:科学出版社,2006.

[2] 郭佳奇,乔春生.椭圆孔口塑性区及其在岩溶隧道工程中的应用[J].铁道学报,2013,35(3):108-114.

[3] 陈 超,李天斌,陈国庆,等.公路隧道挤压型非对称变形解析解研究[J].现代隧道技术,2015,52(5):87-93.

[4] 吕爱钟,张路青.地下隧洞力学分析的复变函数方法[M].北京:科学出版社,2007.

Study on the plastic zone of straight wall horseshoe tunnel under unsymmetrical stress

Xu Xiaoyang

(SchoolofEnvironmentandArchitecture，UniversityofShanghaiforScienceandTechnology，Shanghai200093，China)

Based on the circular tunnel plastic zone solutions and by means of rotating the maximum principal stress direction, an analytical formula for the radius of the plastic zone of surrounding rock around a straight wall horseshoe tunnel under unsymmetrical stress was derived by the complex variable function theory. And a numerical example is given to illustrate the effectiveness of the proposed method.

unsymmetrical stress, straight wall horseshoe tunnel, plastic radius, complex function

1009-6825(2017)15-0157-02

2017-03-17

徐晓洋(1990- )，男，在读硕士

U455

A