标准Ⅱ型马蹄形断面正常水深和临界水深的简化计算

吴国庆

（安康市水利水电勘测设计院，陕西安康 725000）

1 问题的提出

标准Ⅱ型马蹄形断面由于形状比较复杂，正常水深和临界水深的计算有一定的难度。近年来已有学者采用不同的方法对马蹄形断面渠道正常水深进行了研究。文献[1]给出了马蹄形断面正常水深和临界水深的迭代计算公式；文献[2]对正常水深的超越方程采用逐次逼近的拟合方法，获得了最优替代函数，其最大误差为0.66%；文献[3]也给出了马蹄形断面正常水深的迭代公式，并认为计算结果在特征水深点是吻合的，但公式相对较为复杂。文献[4]将马蹄形过水断面正常水深计算转化为非线性优化问题采用实数编码的遗传算法进行求解，但该方法应用比较困难。文献[5]引入准一次函数、准二次函数的概念，对马蹄形两种标准断面正常水深的原函数方程在无量纲正常水深（0.01，1.80）范围内给出了已知流量计算正常水深的简化公式，但未给出已知水深求解流量的方法。文献[6]研究了平底II型马蹄形断面的正常水深和临界水深，引入无量纲参数得到了正常水深和临界水深的直接计算公式。文献[7]研究了标准Ⅰ型马蹄形断面正常水深、弗劳德数和收缩断面水深的计算方法，但未涉及到标准Ⅱ型马蹄形断面的水力计算问题。文献[8]给出了马蹄形断面临界水深的迭代计算公式。文献[9]通过对马蹄形断面临界流方程的数学变换，应用逐步优化拟合原理，得到马蹄形断面临界水深的直接计算式。

由以上综述可以看出，标准Ⅱ型马蹄形断面的正常水深和临界水深虽然已有一些研究成果，除文献[9]对临界水深有直接计算公式外，其余计算方法要么比较复杂，要么还不完善。所以本文根据明渠均匀流理论和临界水深的一般计算方法，通过优化拟合提出了马蹄形断面正常水深和临界水深的直接计算公式。

2 标准Ⅱ型马蹄形断面的基本形式和圆心角

标准Ⅱ型马蹄形断面如图1所示，它由3部分组成，即底部的弓形断面、下部的扇形断面和顶拱的半圆形断面。三圆弧段的半径均为2r，顶拱半径为r，下部弓形断面的圆心角为2α，侧面扇形圆心角为α。由图中可以看出

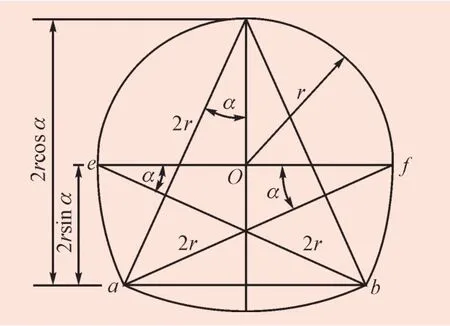
图1 标准Ⅱ型马蹄形断面Fig.1 Horseshoe cross section of standard TypeⅡ

由上式可以解出α=24.29519°，由此可以看出，标准Ⅱ型马蹄形断面的圆心角为常数。

3 标准Ⅱ型马蹄形断面的相对断面面积、相对湿周、相对水力半径和相对水深

将标准Ⅱ型马蹄形断面分为图2中ab线以下（含ab线）的弓形断面、ab线与ef线之间（含ef线）和ef线以上3部分，各部分的断面面积、湿周和水力半径分别计算如下。

3.1 当水深处于ab线以下（含ab线）时

此时水深处于底部弓形断面内，如图2所示，相对断面面积、相对湿周和相对水深分别为

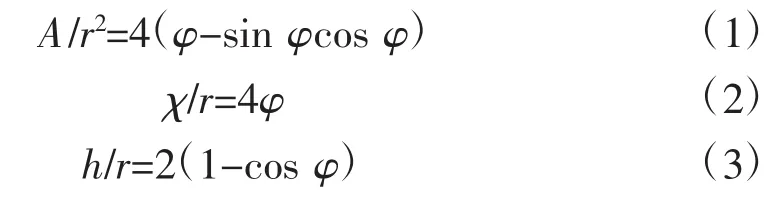
式中，A为面积；h为水深；φ为水深为h时的半圆心角。相对水力半径R为

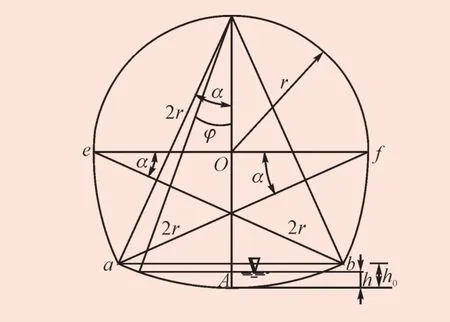
图2 水深处于弓形断面内Fig.2 Water depth at the bottom bow of the cross section

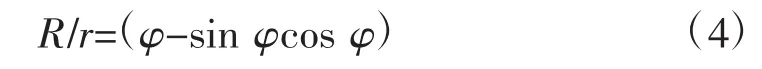
水面宽度为

式中，B为水面宽度，0<φ≤24.29519°。

3.2 当水深处于ab线与ef线之间（含ef线）时

此时水深处于图3中的ab线以上，ef线以下（含ef线）。由图3可以看出，下部水深淹没的面积分为4部分，即图3中的面积A0、A1、A2和A3，其中A2和A3相等。相对断面面积为

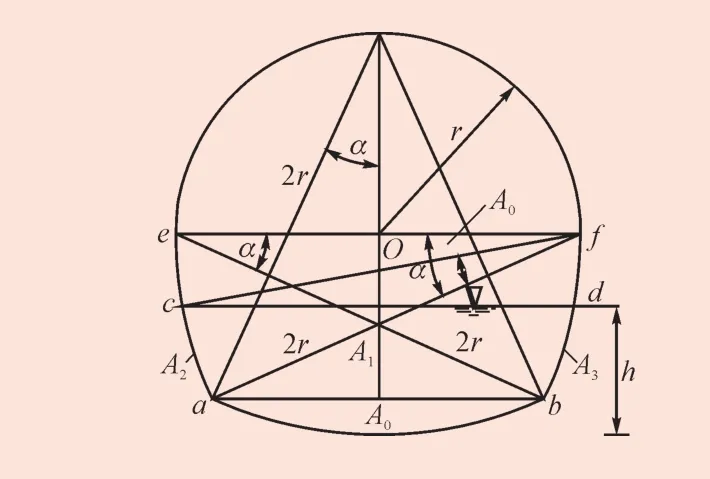
图3 水深处于最大直径（含最大直径）断面内Fig.3 Water depth under the max width of the cross section

相对湿周为

相对水力半径为

相对水深h为

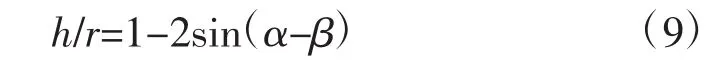
水面宽度为

式中，0<β<24.29519°。

3.3 当水深处于ef线以上时

此时水深处于顶拱半圆形断面内，如图4所示，可以看出，断面面积由图中ef线以下的面积、ef线以上的两个扇形面积和一个三角形面积组成。断面相对面积、相对湿周、相对水力半径和相对水深为

图4 水深位于最大直径以上断面Fig.4 Water depth at profile when water depth is above the maximum diameter

水面宽度为

式中，0<θ<90°。

用以上公式计算的相对断面面积、相对湿周、相对水力半径和水面相对宽度与相对水深的关系见表1。

4 标准Ⅱ型马蹄形断面的正常水深

一般明渠的正常水深流量关系为[10]

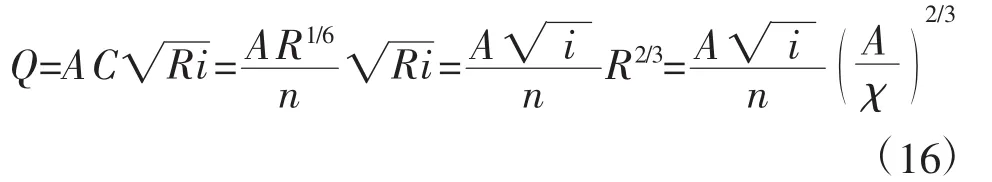
式中，Q为流量；C为谢才系数；R为水力半径；i为渠道的底坡；n为糙率；A为过水断面面积；χ为湿周。

4.1 当水深处于ab线以下（含ab线）时

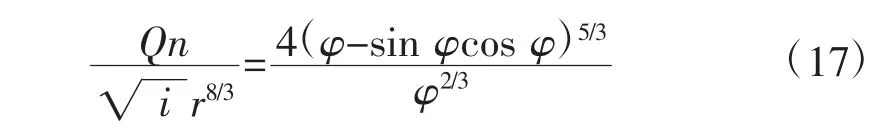
如果已知流量，则可写成迭代公式

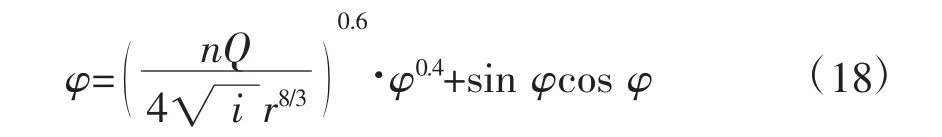
4.2 当水深处于ab线与ef线之间（含ef线）时

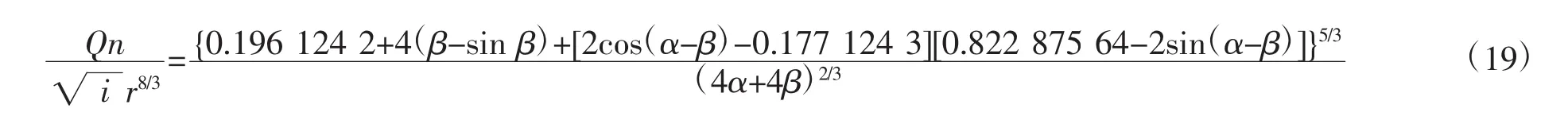
用上式计算水深流量关系时，β的取值范围为0°~24.29519°，如果水深已知，则可由式（9）求出β，代入式（19）即可计算出流量。如果已知流量求水深，可以将式（19）写成迭代公式为

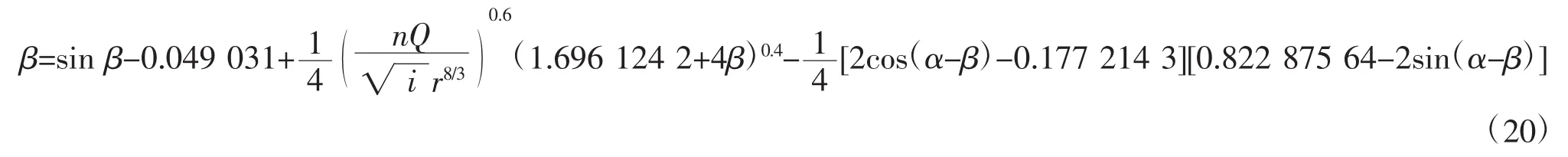
4.3 当水深处于ef线以上时

相对正常水深流量关系为

式（21）中只有一个变量θ，0<θ<90°，计算时如果已知水深，可由式（14）求出θ，代入式（21）求出流量；如果已知流量，则可写出迭代公式为

由以上公式计算的正常相对水深与相对流量的关系亦列于表1中。可以看出，马蹄形断面计算正常水深时需先判断水深所处的位置，然后选用合适的公式，而且计算时均为隐函数关系，不易求解。为了简化计算，分段拟合了与h/r的显函数关系，相对水深或相对流量可以表示为

已知正常水深求流量时

已知流量求正常水深时

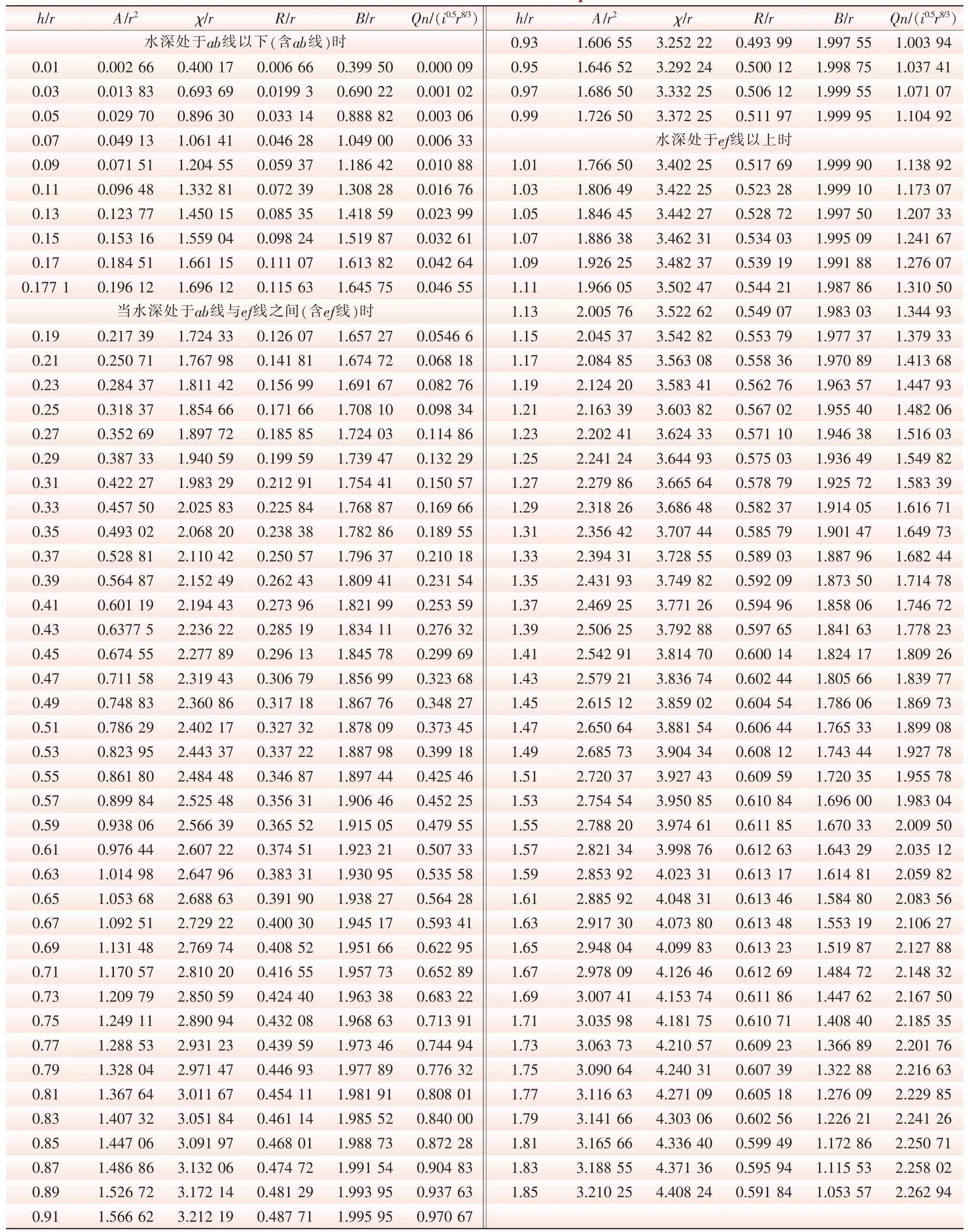
表1 相对断面面积、相对湿周、相对水力半径和相对水面宽度与相对水深的关系Tab.1 The relationship between relative sectional area，relative wetted perimeter，relative hydraulic radius，relative width and relative water depth

公式（23）的最大误差为1.025%，平均误差为0.093%，

公式（24）的最大误差为1.114%，平均误差为0.225%。

5 标准Ⅱ型马蹄形断面的临界水深

明渠临界水深的计算公式为[10]

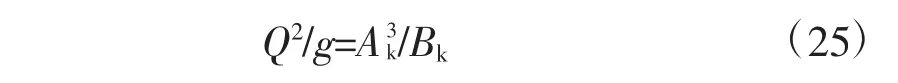
式中，g为重力加速度；Ak为临界水深对应的断面面积；Bk为临界水深对应的水面宽度。

将公式（25）变形为

分段拟合临界水深与Q2/（gr5）的关系为

上式的平均误差为0.337%，最大误差为1.095%。

6 算例

例题1某马蹄形标准Ⅱ型断面，已知顶拱半径r=2.3 m，渠道底坡i=0.00263，糙率n=0.014，试计算正常水深与流量的关系以及临界水深。

解：

用经验公式（23），理论公式（17）、（19）、（21）计算正常水深流量关系，用经验公式（27）计算临界水深。用理论公式计算时，采用试算法，计算结果仍列于表2中。

由以上计算可以看出，本文提出的经验公式计算的流量与理论公式计算的流量最大误差为0.664%；临界水深的经验公式与理论公式最大误差为1.250%，且经验公式判断计算区域明了，过程简单，不需试算，精度完全满足工程要求。

例题2万家寨引黄工程南干1号隧洞的坡降为i=1/1500，n=0.014，r=2.12 m，取其中的两个流量8.6 m3/s和25.8 m3/s计算正常水深，

解：

当流量为8.6 m3/s时，求得将7代入公式（24）得水深h=0.693507×2.12=1.47 m。

当流量为25.8 m3/s时得水深h=1.4542×2.12=3.0829 m

如果用理论公式计算，当流量为8.6 m3/s时，用公式（20）迭代得β=0.2703724，用公式（9）计算得水深为1.47105 m，经验公式与理论公式相差0.0555%。当流量为25.8 m3/s时，用公式（22）迭代得θ=0.479238，用公式（14）计算得水深为3.09754 m，经验公式与理论公式相差0.473%。

表2 例题1正常水深-流量关系及临界水深计算表Tab.2 Example I:calculation table of the relationship between the normal water depth and flow and critical depth

7 结语

本文详细推导了标准Ⅱ型马蹄形断面相对面积、相对湿周、相对水力半径、相对水深和水面相对宽度的计算方法，在此基础上，给出了标准Ⅱ型马蹄形断面正常水深的理论计算公式。为了简化计算，分段拟合了与h/r的关系，给出了均匀流时流量的显函数关系式和正常水深的迭代公式；分段拟合相对临界水深hk/r与Q2（/gr5）的关系，给出了临界水深的简化计算公式。这些公式计算简单，迭代方便，精度完全满足设计要求。为了明确计算过程，通过实例给出了解题步骤，供工程设计参考。

[1] 李永刚.马蹄形隧洞水力计算迭代法[J].人民黄河，1955（11）：42-44.LI Yonggang.Iterative method of horseshoe tunnel hydraulic calculation[J].Yellow River，1995（11）:42-44（in Chinese）.

[2] 腾凯，刘继忠，李松岩，等.马蹄形过水断面均匀流水深的简化计算法[J].人民黄河，1997（1）：36-38.TENG Kai，LIU Jizhong，LI Songyan，et al.Simplified calculation method of uniform water deep of horseshoe cross section[J].Yellow River， 1997（1）： 36-38 （in Chinese）.

[3] 吕宏兴，辛全才，花立峰.马蹄形过水断面正常水深的迭代计算[J].长江科学院院报，2001，18（3）：7-10.LU Hongxing，XIN Quancai，HUA Lifeng.Calculation on normal depth of horseshoe cross section by iterative method[J].Journal of Yangtze River Scientific Research Institute，2001，18（3）:7-10（in Chinese）.

[4]王顺久，侯玉，张欣莉，等.马蹄形过水断面正常水深计算的遗传算法[J].灌溉排水，2002，21（3）：43-45.WANG Shunjiu，HOU Yu，ZHANG Xinli，et al.Genetic algorithm for calculating normal water depth of horseshoe cross section[J].Irrigation and Drainage，2012，21（3）:43-45（in Chinese）.

[5] 赵延风，王正中，芦琴.马蹄形断面正常水深的直接计算公式[J].水力发电学报，2012，31（1）：173-177.ZHAO Yanfeng，WANG Zhengzhong，LU Qin.Direct calculation formulae for normal depth of horseshoe section[J].Journal of Hydroelectric Engineering，2012，31（1）:173-177（in Chinese）.

[6]文辉，李风玲.平底马蹄形断面的水力计算[J].农业工程学报，2013，29（10）：130-135.WEN Hui，LI Fengling.Hydraulic calculation of horseshoe cross-section with flat bottom[J].Transactions of the Chinese Society of Agricultural Engineering，2013，29（10）:130-135（in Chinese）.

[7]张志昌，李若冰.标准Ⅰ型马蹄形断面水力特性的研究[J].长江科学院院报，2013，30（5）：55-59.ZHANG Zhichang，LI Ruobing.Hydraulic characteristics of standard I-Type horseshoe cross section[J].Journal of Yangtze River Scientific Research Institute，2013，30（5）:55-59（in Chinese）.

[8] 吕宏兴.马蹄形过水断面临界水深的迭代计算[J].长江科学院院报，2002，19（3）：12-14.L譈Hongxing.Calculation on critical depth of horseshoe cross-section by iterative method[J].Journal of Yangtze River Scientific Research Institute，2002，19（3）:12-14（in Chinese）.

[9] 张宽地，吕宏兴，陈俊英.马蹄形过水断面临界水深的直接计算法[J].农业工程学报，2009，25（4）：15-18.ZHANG Kuandi，L譈 Hongxing，CHEN Junying.Direct calculation of critical depth of horseshoe section tunnel[J].Transactions of the CSAE，2009，25（4）:15-18 （in Chinese）.

[10]张志昌.水力学（下册）[M].北京：中国水利水电出版社，2011：69-90.