斜辊矫直机辊形理论的新探索

崔甫

·专题综述·

斜辊矫直机辊形理论的新探索

崔甫

(东北大学，辽宁沈阳110819)

本文论述了斜辊矫直过程中，采用等曲率反弯矫直的优越性以及在改变工件直径、反弯曲率半径和工作斜角条件下仍可获得等曲率反弯矫直效果的可能性。正确运用这种辊形的特殊功能，矫直技术的发将会有较大的发展。

双曲线辊形;圆柱形辊形;等曲率

0 前言

圆材矫直所用的斜辊矫直机经历了百年左右的生产实践和不断改进，已经发展成为多品种、多种结构和规格齐全的矫直设备，同时在辊形方面也已派生出双曲线辊形、圆柱辊形和等曲率反弯辊形等新内容。实践证明这些辊形在正确调节前提下都能很好地完成矫直任务，究其原因是已经认识到的这些辊形都具备一种本质性的等曲率压弯功能，只不过它们之间没有得到沟通，互不相识。但经过采用等曲率反弯辊形后才证明它们是一种辊形的三种表现形式。因此，很有必要把三种辊形整合起来，都用等曲率反弯辊形的优越性能把斜辊矫直技术提升一大步。

1 等曲率反弯辊形的形式

双曲线辊形与圆柱辊形都是以其几何特征来命名的，而近年出现的等曲率反弯辊形则是以其弹塑性反弯矫直功能来命名的。三种辊形既具有本质上的共同性，又有外形上的明显差别。首先就双曲线辊形来说，其设计所用的曲率值为零，斜角值为任意值(根据经验确定某一斜角值)。在这种斜角状态下算出包络直棒的辊面半径值就是双曲线辊形，这个辊形对于直棒表面既可以说是等曲率压紧，又可以说是零曲率“压弯”。

再说圆柱辊形在圆柱辊面与圆材表面压紧条件下，若两者相互平行(斜角为零)，圆材必将处于直线状态;若两者相互倾斜，圆材必将被压成螺旋线包络在辊面上，此螺旋线各处的斜角必将一致，各处的曲率也将一致，所以说圆柱辊形是最直观而且是无需证明的等曲率反弯辊形。上述两种辊形的设计都与反弯矫直所需要的反弯曲率脱离了关系，也与工作倾斜角之间失去了联系，直到今天也很少有人明白这两种辊形矫直圆材除了运动学上的需要之外，还会有什么矫直学的重要意义?只有在等曲率反弯辊形问世之后才逐渐理解:唯有按反弯矫直所需要的反弯半径和矫直速度所需要的斜角来调节，并按结构强度要求设计的等曲率反弯辊形才是真正实用的辊形。

2 等曲率反弯辊形矫直的反弯半径和斜角

表1 将Φ30 mm圆钢按α=20.55°压成ρ=927 mm弯度的圆柱辊形Tab.1Cylindrical roll-shape as with ρ=927 mm straightening Φ30 mm bar under α=20.55°

本文结合实例来进一步认识等曲率反弯辊形的实质内容。先采用D=200 mm，α=20.55°的矫直辊对直径d=30～60 mm，σs=1 000 MPa，E=206 GPa的圆钢，按ρ=927 mm反弯半径进行反弯矫直。利用文献［1］中公式(4－10)～(4－17)算出辊形半径R见表1。取整后的辊径D =2R=200 mm。

这个辊径由辊腰到辊端完全一致，表明辊形为圆柱形。矫直时的工作导程t=π×d×tanα= π×60×tan20.55°=71 mm，辊子工作长度lg= 75×2=150 mm。可见lg＞2t=142 mm，可以获得可靠的矫直质量或均一的弯度。当斜角改变时，反弯半径ρ也必将随之改变，即矫直能力也随之改变，但其等曲率特性不变，因为圆柱表面上任河一条螺旋线的等曲率特性在全长度上都是一致的。

再按α=15°设计双曲线辊形，辊腰直径不变，圆钢的材质及直径都不变，算出的双曲线辊形见表2。

表2 按α=20.55°对Φ30 mm直棒进行压紧的双曲线辊形Tab.2Hyperbolic roll-shape as straightening Φ30 mm bar under α=20.55°

这个辊形只能压紧直棒，要想将直棒压成精确的弯度，达到反弯半径ρ=927 mm时，必须增大斜角使其达到α=25.16°。于是，按α= 25.16°及ρ=927 mm设计的曲率反弯辊形，结果与表2中的辊形完全一致，这就证明了双曲线辊形也是等曲率反弯辊形。

上面两个特殊等曲率反弯辊形都有其特色的缺点，就是都无法根据反弯需要确定应调的工作斜角，也无法根据斜角确定反弯半径，所以它们都必将被等曲率反弯辊形所取代。

根据等曲率反弯辊形中反弯半径与斜角关系可知，它们都是辊形计算所需的重要参数，而且互相关联，不是一种简单数理关系，所以需要结合数理来理解它们之间的关系并找出它们之间的变化规律。

3 等曲率反弯辊形的矫直实例

图1为2－2(8)辊系的斜辊矫直机，其中8个矫直辊共形成两种反弯过程。当圆材经过入口导向套A后由第Ⅰ对辊缝咬入经第Ⅱ对辊缝被压成ρ1的弯度，又经第Ⅲ对辊缝被压成ρ2弯度，最后由第Ⅳ对辊缝经过出口导向套B送出矫直机。图中两种反弯半径ρ1及ρ2都是在特定的辊子斜角α条件下形成的。第三种反弯半径ρ∞也是在α条件下确定的。入口导套可以防止因原始弯曲严重所造成的甩摆，出口导套可以清除矫直后的残余弯曲。再具体的结合对棒材Φ30 mm的矫直过程来讨论。第一次反弯需要ρ1=927 mm，第二次反弯需要ρ2=1 850 mm，其工作斜角定为α=30°，各压紧辊的反弯半径ρ∞可以用ρ∞= 1 000 000 mm代替。按本文的辊径及辊长可算出图1中三种辊形半径见表3。

由于这种辊系尚需要矫直Φ30 mm以上到Φ60 mm棒材，故需进一步观察棒材直径变化时反弯半径随之变化的情况，以及辊子斜角随之变化的情况。ρ1及ρ2变化正比于直径，变化很容易算出，见表4，ρ∞值不变。辊子斜角变化见表5。

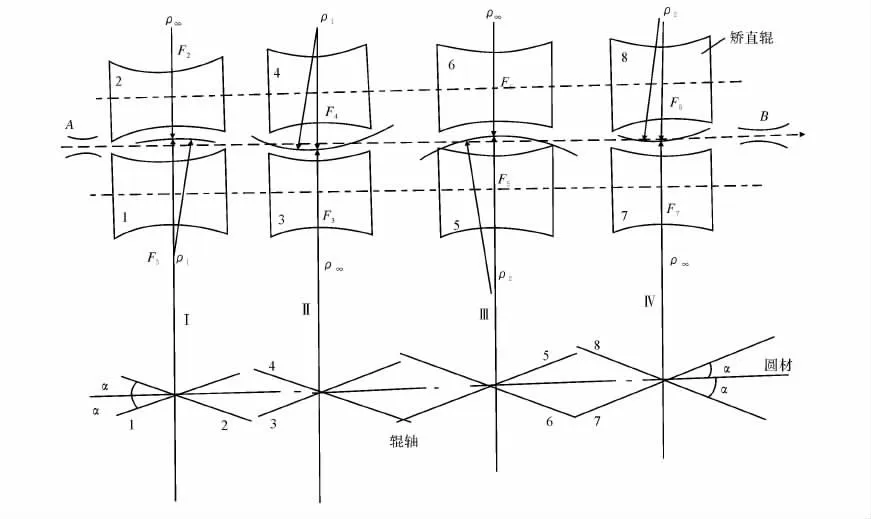
图12 －2(8)辊系Fig.1Straightening roller system of 2－2(8)

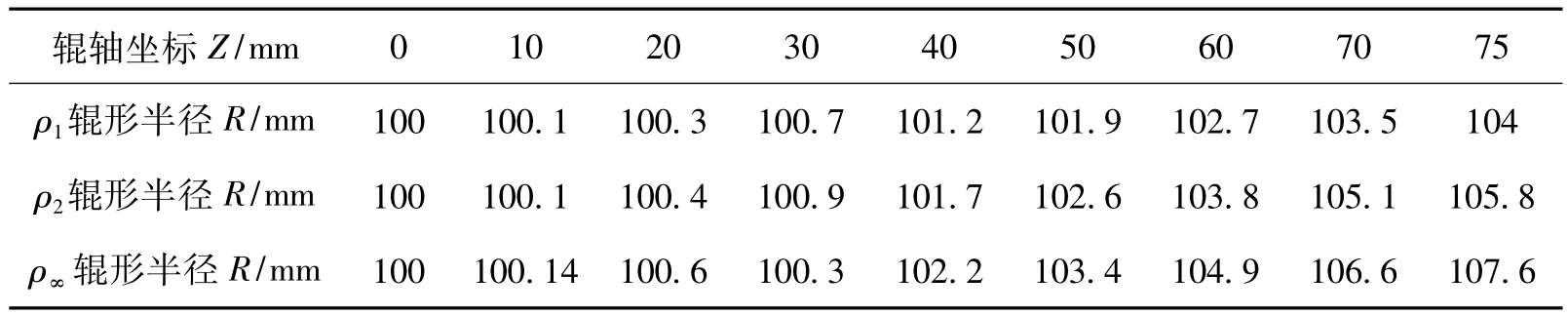
表3 矫直Φ30 mm圆钢按α=30°算出的辊形Tab.3Reversed-bending radius as straightening Φ30 mm bar under α=30°

表4 各种直径圆材在矫直时应达到的反弯半径Tab.4Reversed-bending radius which should be as straightening different diameters bar

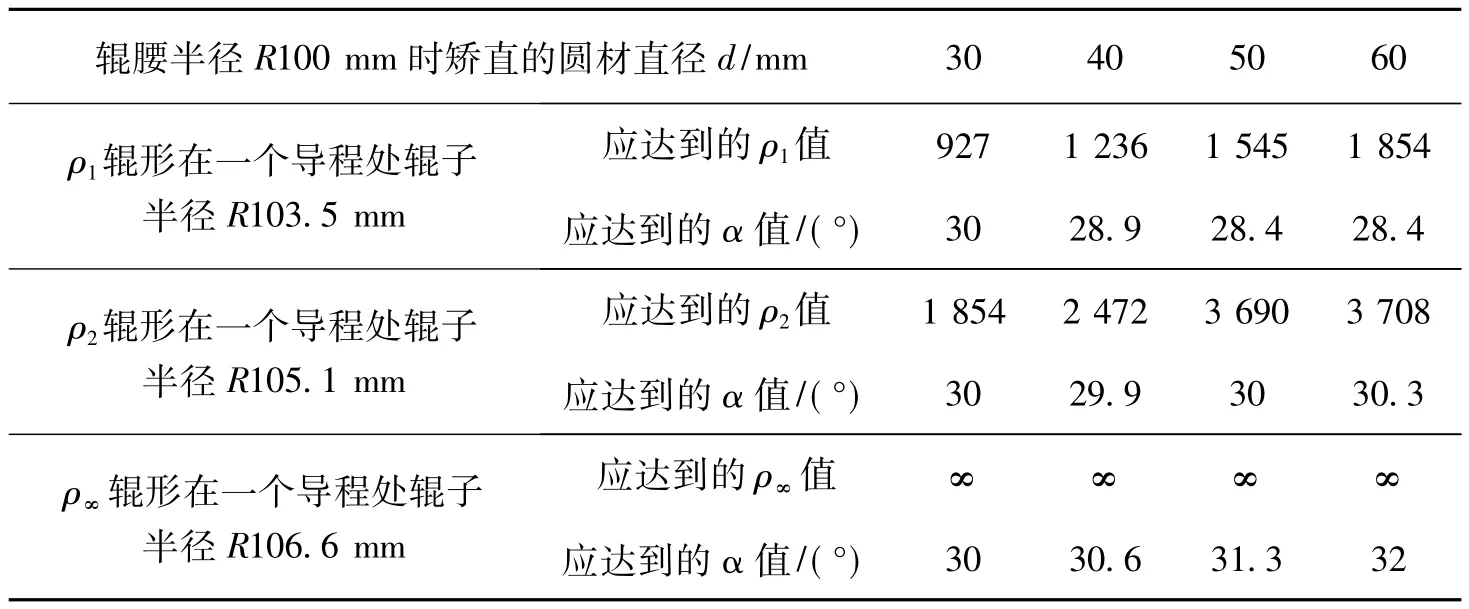
表5 四种直径圆材通过三种辊形矫直时的辊子斜角Tab.5Bevel angle of roller as straightening bar four kinds of diameter by three types roll forming

由于斜角值是按已定的辊形(表3)并采用迭代法求知的，既麻烦又费时，故拟用表5中四种棒材及其对应的斜角做出曲线如图2所示。由斜角曲线可得到调角规律，同时也可知调角范围最大为30+－21.6(°)，最小为30+－00..31(°)，只要不影响工作稳定性，调角是允许的。当调角范围很小时，如不超过1°时，不调角也可以正常矫直。为了扩大矫直范围，可用此辊系矫直Φ15～Φ30 mm的圆材，此时辊子斜角须按图2中虚线规律来调节，但是实际上还可用加大滚压力的办法使圆材表面的外弯侧增大拉伸变形，使弯曲中性层内移达到等效增加弯度，完全可以达到矫直细棒的目的。在理论上也完全符合米塞斯屈服准则的要求。再进一步探讨用这种辊系矫直Φ60 mm以上的圆材时，首先需要验算机械的结构强度，在强度允许条件下，还要验算辊面工作长度不能小于一个导程。这些条件都允许之后可用加大辊缝的办法矫直粗棒。斜角也须按照曲线规律适当微调。等曲率反弯辊形不仅可用来完成双曲线辊形和圆柱辊形所能完成的矫直任务，而且还能完成他们无法完成的矫直任务，可以做到高效和精确。三段等曲率反弯的二辊式矫直机就是这一实例的证明。将原始弯曲很复杂的棒材送入辊缝之后，一次通过便可以完成三步反弯矫直任务，可以在很多生产部门取代多斜辊矫直机。

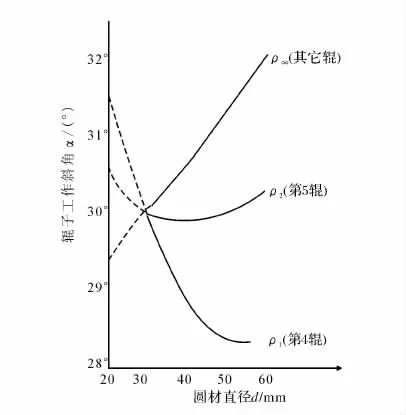
图22 －2(8)辊系矫直Φ30～60 mm棒时斜角值Fig.2Bevel angle of roller system for straightening Φ30～Φ60 mm bar

4 结束语

从三种辊形的整合对比中看到了等曲率反弯辊形不仅涵盖了前两种辊形，而且具有准确反弯矫直功能和明确的与反弯半径对应的辊子斜角。把辊形半径、反弯半径与辊子斜角联系在一起，并建立起这些参数间的数理关系使辊形设计走上简捷、严密、正确的道路。使矫直质量得到了可靠保证，使工艺调整简单准确。在辊形理论的发展上取得一次很大进步。

［1］崔甫．矫直原理与矫直机(2版)［M］．北京:冶金工业出版，2005．

［2］崔甫．矫直技术与理论的新探索(2版)［M］．北京:冶金工业出版，2014．

［3］崔甫，杨会林．关于矫直技术领域中一些认识新区的讨论［M］．重型机械，2015(01)．

［4］崔甫．矫直理论与参数计算(一)［J］．重型机械，1985(07)．

［5］崔甫．矫直理论与参数计算(二)［J］．重型机械，1985(08)．

［6］崔甫．矫直理论与参数计算(十三)［J］．重型机械，1986(07)．

［7］崔甫．矫直理论与参数计算(三)［J］．重型机械，1985(09)．

［8］崔甫．矫直理论与参数计算(四)［J］．重型机械，1985(10)．

［9］崔甫．矫直理论与参数计算(五)［J］．重型机械，1985(11)．

［10］崔甫．矫直理论与参数计算(六)［J］．重型机械，1985(12)．

［11］崔甫，施东成．矫直机压弯量计算法的探讨［J］．冶金设备，1999(01)．

［12］崔甫．对矫直技术领域中一些认识误区的讨论［J］．重型机械，2013(02)．

［13］崔甫，庄振海．二辊式矫直机的圆弧辊型［J］．冶金设备，1985(03)．

［14］崔甫．关于弹塑性弯曲的极值问题［J］．重型机械，1991(06)．

［15］刘树桐，崔甫，郑丽君．二辊矫直机采用双向圆弧辊型的设计实例［J］．有色设备，1987(02)．

殞专利介绍

一种坯料长度检测系统(CN 105710139 A)

本发明的目的在于提供一种坯料长度检测系统及检测方法，该系统具有结构简单、功能完善、可靠性高的特点，该方法的投入可以实现停机上料型冷轧。

一种坯料长度检测系统，包括在轧管机上料床身的上料电机上安装的用于记录推料杆位置的编码器，安装在上料床身的末端也就是推料杆的待推料位置的作为编码器的零位标记位检测的上料零位检测开关，安装在上料零位检测开关之后的用于上料零位检测开关失灵后的极限位报警的上料后极限检测开关，安装在推料杆顶端即顶料侧的随推料杆一起移动的用于检测顶料杆是否顶住坯料的推料杆顶端检测开关，安装在上料床身前端的作为坯料长度一个点检测的坯料测长检测开关，安装在上料床身的前端极限位即推料杆将坯料推入送料小车顶门前位置的用于停止上料电机输送坯料的上料停止检测开关。

本发明通过编码器和检测开关检测出坯料的长度，利用料架上和上料床身内已有料检测开关实现上料动作的全自动;不仅可以降低由于人工操作失误带来的生产事故，同时由于简化了上料过程也提高了生产效率。

New exploration of rolling theory in cross roll straightening machine

CUI Fu
(Northeaster University，Shenyang 110819，China)

In this paper，acomprehensive answer to the superiority of anti-bend straightening curvature in cross roll straightening and the possibility of obtaining anti-bend straightening curvature effect under the condition of changes in the diameter of the workpiece，the anti-bending radius and angles are given．The proper use of this special feature will create more favorable conditions of straightening technology for future development and bring a revolutionary change．

dual-curve roll shape;cylindrical roll shape;equal curvature

TG333

A

1001－196X(2017)01－0002－05

2016－05－22;

2016－08－22

崔甫(1928－)，男，东北大学教授，主要研究矫直理论。