供热计量条件下用户用热博弈模型研究
2017-07-01赵宇,陈锐,3,廖原
赵 宇,陈 锐,3,廖 原
(1.中国科协创新战略研究院,北京 100863;2. 中国科学院科技战略咨询研究院,北京 100190;3. 中国科学院大学,北京 100049)
供热计量条件下用户用热博弈模型研究
赵 宇1,陈 锐1,3,廖 原2,3
(1.中国科协创新战略研究院,北京 100863;2. 中国科学院科技战略咨询研究院,北京 100190;3. 中国科学院大学,北京 100049)
考虑热费分户计量过程中存在户间传热的问题,将户间传递的热能看作是私人供给的公共物品,从公共品私人共享博弈的角度研究民用建筑内住户间用热博弈模型,基于居民用热的科布-道格拉斯效用函数得到不同位置住户在采暖热费用方面的补偿机制,平衡了住户间收退费差异。通过北京某一热计量建筑的实证研究表明,本文提出的热费补偿计算有效地解决了边角住户温度低、用热大,中间住户温度高,用热少的现实问题,有利于热计量工作的大面积推广。
供热计量;户间传热;公共物品;博弈论
1 引言
在我国大力推行节能减排工作的趋势下,近年来来各地方政府开始着手推进分户供热计量改革,分户热计量能够极大地促进消费用户主动的行为节能;实现按需供热,减少过度供热和供热不足的现象;促进供热企业提高综合效率;提升建筑围护结构保温性能;减少水力失调现象等等[1]。然而目前供热计量改革的步子缓慢,各方对供热计量改革的认识和思路变得模糊[2]。这主要由于目前热计量工作无法被广大群众正确认识并开始实施大面积的计量收费工作造成的,这个问题的根源主要来自三方面,一是在收费层面迟迟不能确定热价标准;二是不能真正解决建筑中不同部位的房间同样采暖效果但需热量却相差几倍的问题,很难通过一些“修正系数”缓解这一矛盾;三是目前的分户热表可应用性很差,不能解决定期标定、故障排除等巨大的服务需求问题,很难真正依靠这一尚不“精确”的系统进行实际收费[3]。可见合理制定收费方式是解决热计量推广问题的关键所在,这需要对热计量过程中用户的用热过程开展研究。
在未实施分户热计量前,用户热费按面积计算,根本没有调节阀门开展行为节能的动力;实施分户热计量后,在“多用热多缴费”的作用下,用户会根据自身需求调整阀门开闭,达到节能目的。但由于热具有传递性,邻居之间分别根据自身需要调节阀门,热量在存在温差的邻室之间传递,无形中用户与其周围邻居发生了用热的博弈行为。表面上看,分户计量使得热量成为用户可以享用的私有产品,但由于热的传递性,热量在某种程度上成为一种公共物品。这种部分公共属性的热具有非排他性和非竞用性,必然会造成邻居间“搭便车行为”的产生。反映在实际中是居住在建筑边角的用户温度上不去却耗热量大,中间的用户温度适宜却耗热量少的倒挂现象。考虑到边角用户对中间用户具有“保温”的作用,其多用掉的热量应部分地由中间住户提供“补偿”,这种补偿如何科学地量化目前还未见研究。
本文基于公共品私人自愿共享博弈分析的思路,通过分析相邻用户之间在用热博弈过程中所达到均衡状态研究这种用户间相互的用热“补偿”,使得补偿标准能够科学地量化,有助于热计量工作的大面积推广。第二节介绍关于公共品私人自愿共享博弈分析及相关研究,第三节建立用户间用热博弈模型并对量化的补偿开展分析,最后是总结和对热计量推广的政策建议。
2 问题描述及模型介绍
热计量条件下的用热博弈中,住户享有各自的私有物品(散热器发热),非自愿地提供公共品(公共热),以保障采暖季基本用热生活为底线,相互之间基本不了解各自的生活习惯和用热偏好,只根据自身的习惯调节阀门控制用热量。热量从温度高的地方传递到温度低的地方,一家散热器的热量调节会对其邻居造成影响,邻居根据变化调节散热器以修正这种影响,无形中形成用热博弈过程。信息不完全共享、不合作是这一问题的典型特征。可以说这个问题是一类特殊公共品共享的博弈研究。
对于公共物品的分析研究很早就已开始,1919年林达尔提出了公共物品概念,萨缪尔森[4]定义公共物品是“每个人对这种物品的消费都不会导致其他人对这种物品消费的减少”。公共物品私人供给的经济模型是由Bergstrom,Blume和Varian[5]在1986年的文章中证明并发展的,可以用于许多经济问题的解决。
热量在户间传递相当于共享热能,而在用热博弈中,这种共享很大程度上是非自愿的共享,但住户却无力改变这个事实。对于本文的住户用热领域的博弈,住户之间一般不会就用热偏好和策略发生直接信息沟通,各自在自己效用最大化的目标下调节散热器散热量,每个散热器贡献一部分的公共热,每个住户与其周围的邻居都从这部分公共热中获益。缪勒指出即便在博弈者之间缺乏直接沟通的情形中,只要每个博弈者都选择一种超级博弈策略(公共物品消费者正确表述对公共物品的需求),就能把他在某一次博弈中选择的合作策略与另一位博弈者对这种策略的选择联结起来,出现合作解[6]。Rubin[7]通过重新界定了社会资本的内涵,并采用完全信息静态博弈模型研究了企业网络中社会资本的自愿供给问题。与穆勒的结果一致,企业社会资本的供给决策过程中,纳什均衡解是可以达到的,但它小于帕累托最优解。对热计量收费而言,合作解是对仪表计量费用的再分配过程,住户既是公共品的提供者也是受益者,只是供给与收益比例不同,相互之间存在利他和利己的行为,这种基于收益分配的公平偏好模型主要有FS模型和ERC模型,这方面Rabin做了大量的理论研究工作[8-10]。在Bergstrom[11]中,De Marco和Morgan定义了轻微利他均衡,并且证明了轻微利他均衡的存在性[12]。石军伟和胡立君[13]在多目标博弈中定义了弱帕累托-纳什轻微利他均衡,并且证明了弱帕累托-纳什轻微利他均衡的存在性。
在非合作博弈方面,侯光明和李存金[14]根据管理激励与约束机制的特征,建立了单阶段和多阶段管理激励与约束非合作博弈机制式表述的基本模型及方法,模型将复杂的多因素、多目标、多阶段博弈问题完整地表达,为人们研究复杂博弈问题提供了新的理论工具。陈潭[15]研究了公共事务管理中非合作博弈下的集体行动,指出可能会出现的公共产品供给短缺、公共资源利用无度、公共秩序混沌无序、公共组织效率缺失、公共政策执行失范等请多问题,并提供应对这些问题的政策建议。淮建军等[16]用Selten方法,分析了地方政府和房地产商俩个体的非合作讨价还价过程,得出地方政府和房地产商之间的非合作讨价还价有助于加强管制的结论。吴云和周青[17]运用非合作博弈模型分析了两个团队产生冲突后的可能后果,得到低团队冲突不利于团队创新,会使团队停滞不前;而过度团队冲突又会妨碍团队目标的实现的结论。张斌和华中生[18]分析了下游制造商和供应商就产品质量检验方案选择的非合作博弈过程,提出使制造商获得更大期望收益的抽检方案。刘军和李成金[19]讨论了两个企业对具有一定替代性的两种产品的完全信息动态产量一价格二维博弈模型及其均衡,指出要充分考虑无差别产品之间替代性,这样选择的产量和价格策略才是最优。
从公共物品私人供给的决定方式角度出发,可以分为替代型、互补型和包含型公共品[20],不同类型的公共品纳什均衡点不同,不同用户供给的公共热属于替代型公共品。用户在使用这类可替代的公共热过程中的博弈是典型的非合作博弈。在与热力系统类似的电力系统中,张荣和张宗益[21]研究了电力上网竞价博弈过程中如何通过利用需求信息提高自己的长期利润,两家电厂分别根据对方的行动选取自己的最优决策;在环境效率评价中,经济生产子系统和污染物处理子系统也存在与本文类似的非合作博弈,卞亦文[22]通过分析两子系统各自运行效率,提出一种能够同时评价决策单元整体效率和其子系统效率的DEA方法。目前在与热计量有关的领域研究多集中在宏观层面,如通过信号博弈研究政府对企业节能补贴政策,发现市场完全成功均衡的关键条件是要提高企业造假的伪装成本和期望风险成本[23];研究热计量实施后政府、用户、供热企业各自面临的困境分析[24],研究既有建筑节能改造外部性的危害及其对节能改造的影响,设计相应的激励政策[25]。通过静态博弈论研究两个热用户在不同供热收费模式下彼此间用热行为的相互影响[26]。多数应用博弈论的研究都是探讨各利益主体彼此关系,而在微观尺度层面,目前尚未涉及将住户的部分热量作为公共物品看待的问题,本文将住户间热传递看作私有物品共享成为公共物品,参考公共品私人自愿共享博弈模型,从微观的研究视角探讨这种过程对最终热费计算的影响并分析相关结论对供热计量推广政策的作用。
3 用户间用热博弈模型与分析
3.1热费计量模型与热量分布特征
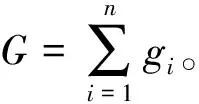
Li=ui(xi,G)+λ(Mi-pxxi-pGgi)λ是拉格朗日乘数。
取得最优时,最优化一阶条件为:

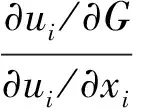
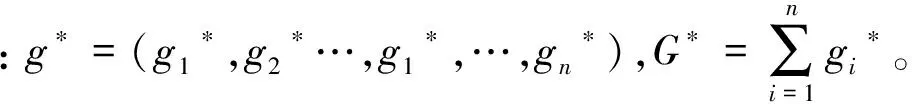
假定个人效用函数为科布-道格拉斯形式:ui=xiαGβ,这里0<α<1,0<β<1,α+β≤1。科布道格拉斯函数属于规模报酬不变的齐次函数形式,此时个人最优的均衡条件是:
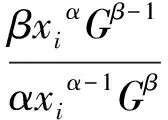
将预算约束条件代入并整理,得反应函数:
从上式中可以看出,当一个人相信其他人提供的公共物品越多,他自己的供给就越少。
热源供热费用由固定成本和变动成本两部分组成。固定成本中包括折旧费、大修费、企业管理费,人工费。变动成本中包括燃料和动力费、小修费及其它一些费用(供热企业收费有一定的损失或应考虑其它因素),变动成本和用户用热量的多少密切相关。基本热价就是固定成本除以总供热面积,计量热价就是可变成本除以总的销售热量。固定成本中的各项费用都是与热用户使用热量的量无关的部分,无论热用户用热与否,用热多少,供热公司都要付出;可变成本是与热用户使用热量的量有关的部分,若热用户不用热或者热用户少用热,供热公司就可以少消耗的部分。因此:居民用热总成本=固定成本+计量热价×用户用热量。
根据热力学定律,住户享用的热量与其室温成正比。一般情况下,处于边角的住户温度相对低,处于中间的住户温度相对高,不考虑太阳光的辐射传递作用,热量由各家散热器发出,受局部温差的影响在户间传递并与外界交换,最终达到稳定状态。如图1所示,用颜色的深浅表示温度的高低,总体而言,热量由温度高的区域向温度低流动,边角住户由于和自然界接触面积较大,因此主要由其与外界发生热交换,维持整体楼栋的热流平衡;中间住户受到边角住户对其形成的保温作用,能够在较少热量消耗下维持较高的室温。这是目前我国采用供热计量居民建筑内热量分布的基本特征。

图1 户间传热示意图
3.2变量说明
为了便于后文的博弈和补偿的分析工作,现将博弈模型所需的主要变量说明如下:
xi表示第i个住户热计量仪表记录的用热量。
gi表示第i个住户对其它住户的散热量。
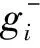
ai表示i住户的热耗散系数。
bi表示i住户的吸热系数

U(xi,Gi)表示i住户的用热效用函数
px表示供热单位制定的单位能耗所对应的热价(私有物品价格)。
pg表示用户通过传热获得的热量的热价(公共物品价格)。
Mi表示第i个住户采暖的理论费用。
Mi*表示第i个住户采暖的实际费用。
D表示住户采暖所花费的固定费用。
散热量gi与记录热量xi一般是线性关系,即建筑材料和结构一定,耗散系数ai保持不变,用热量越大,耗散的热量也越大,
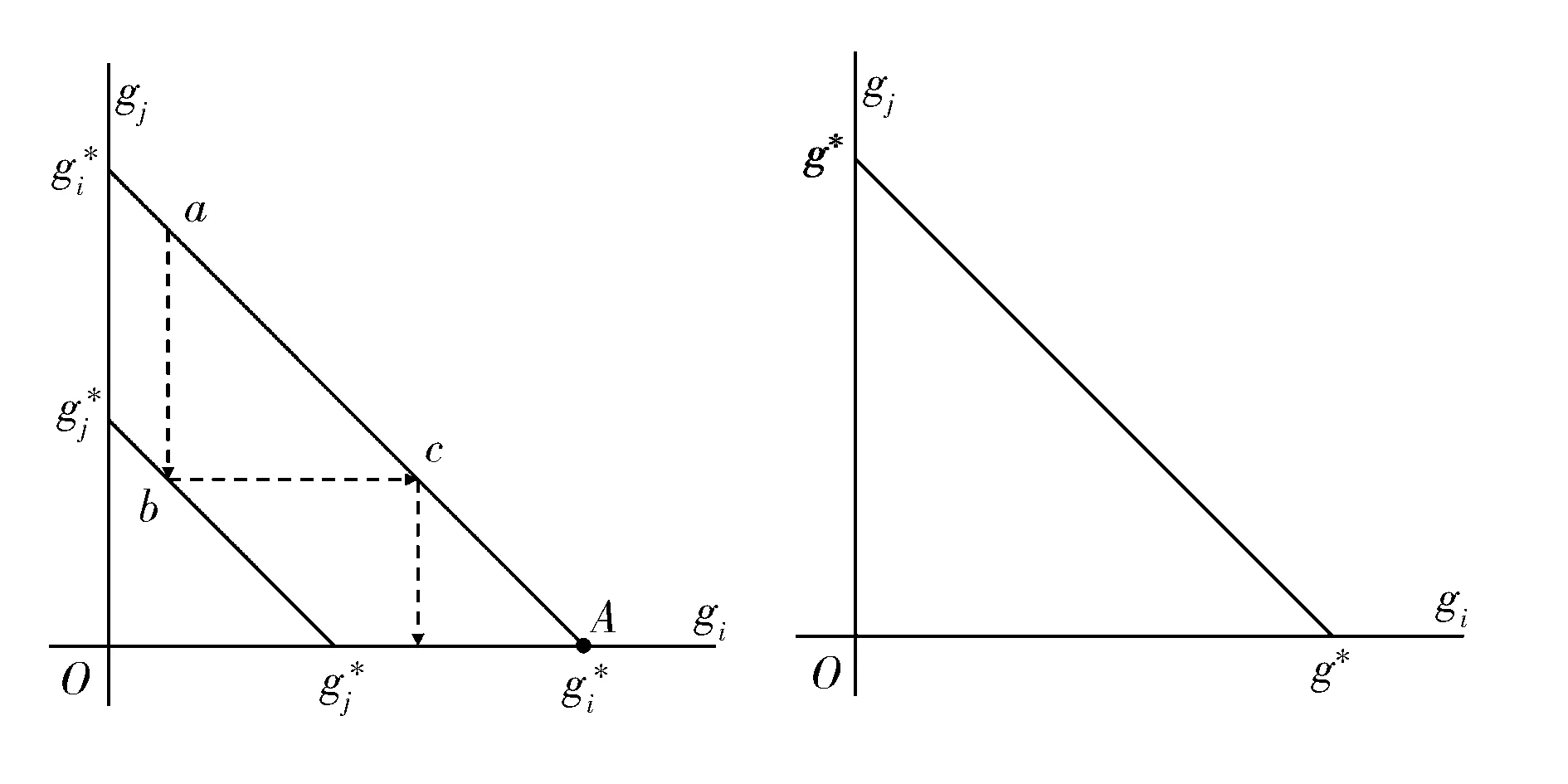
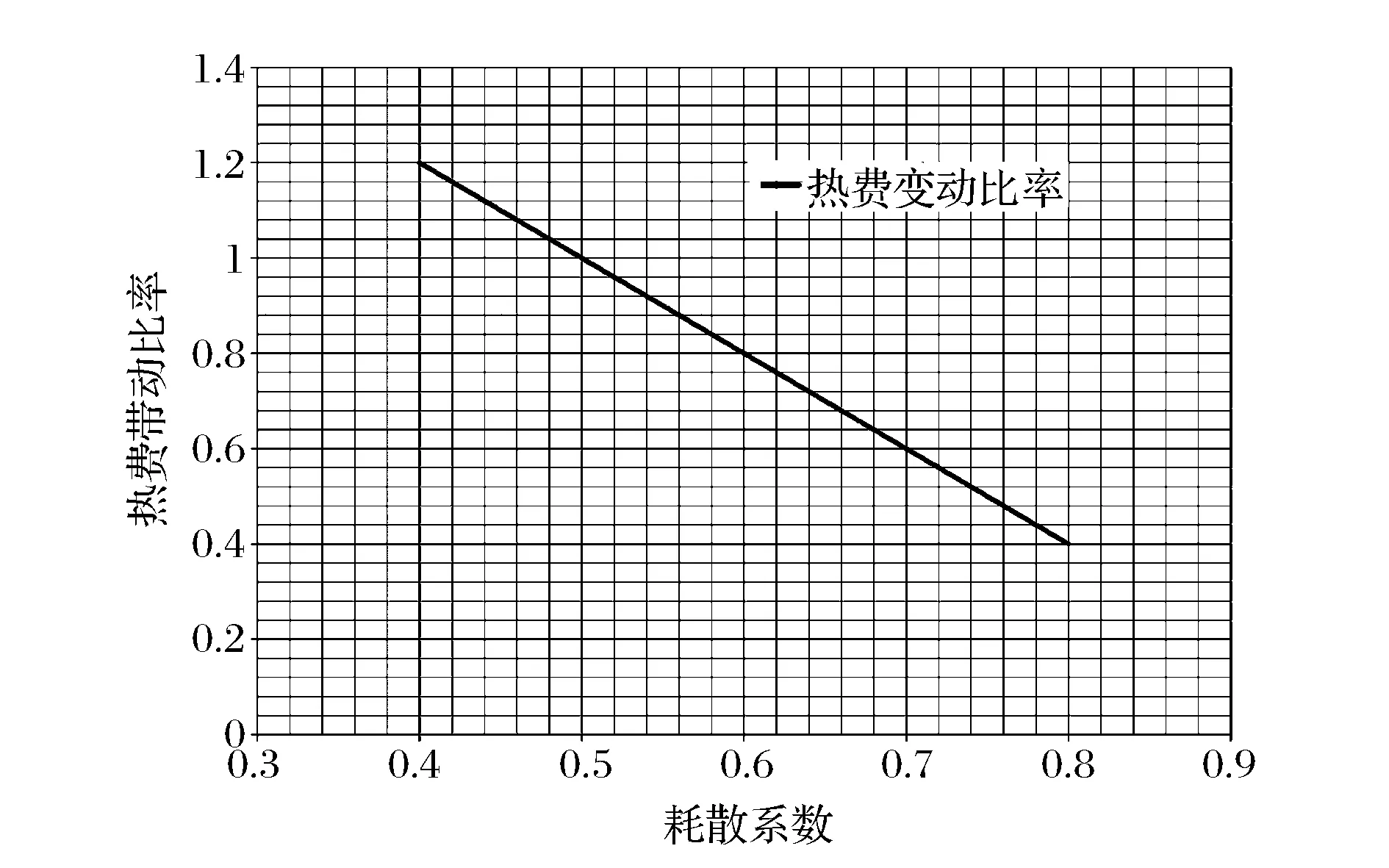
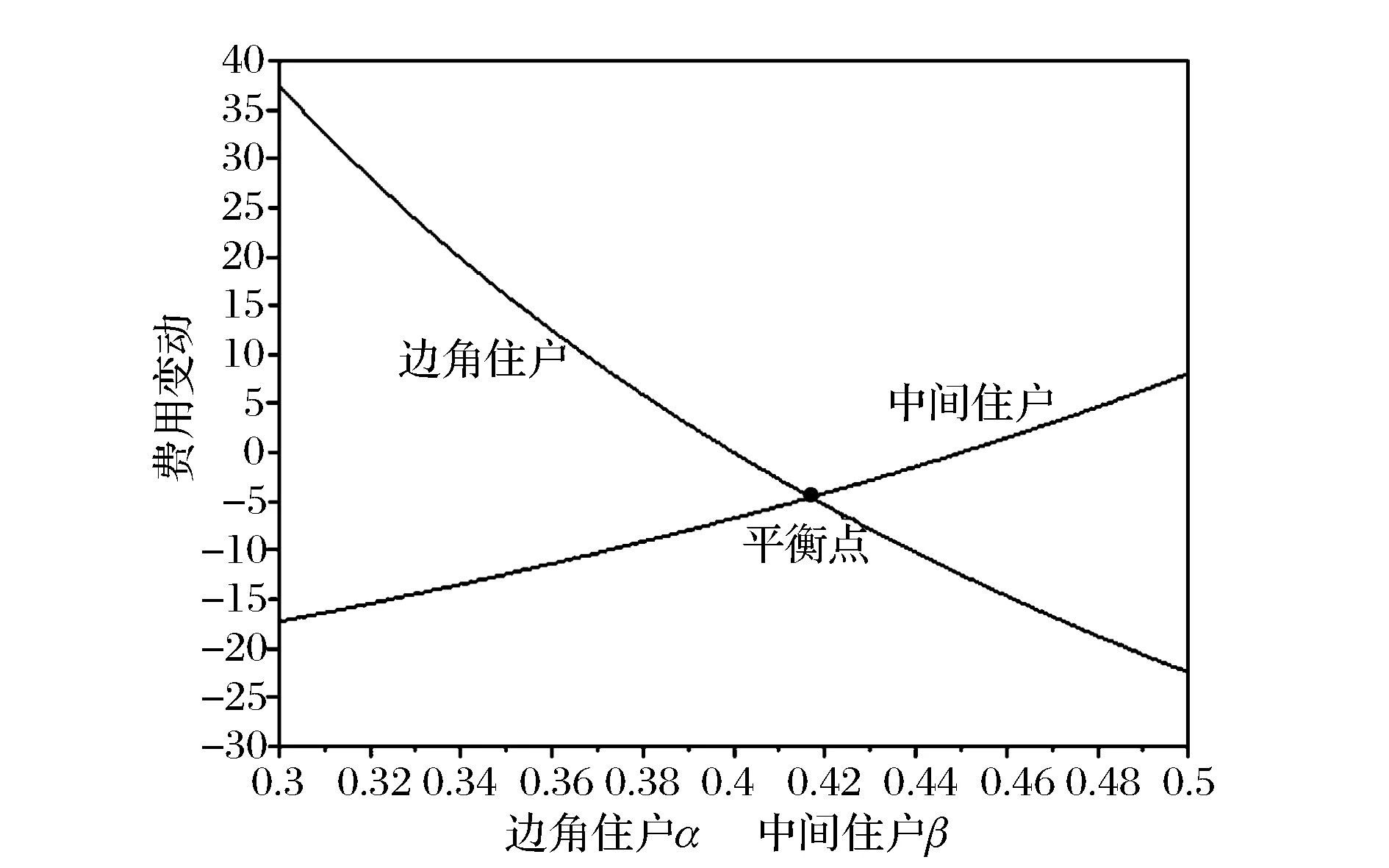
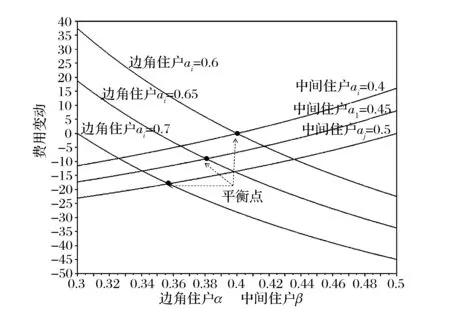
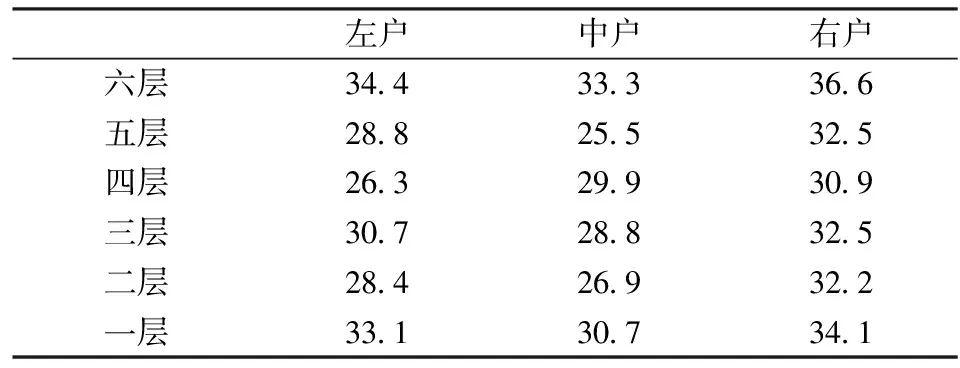
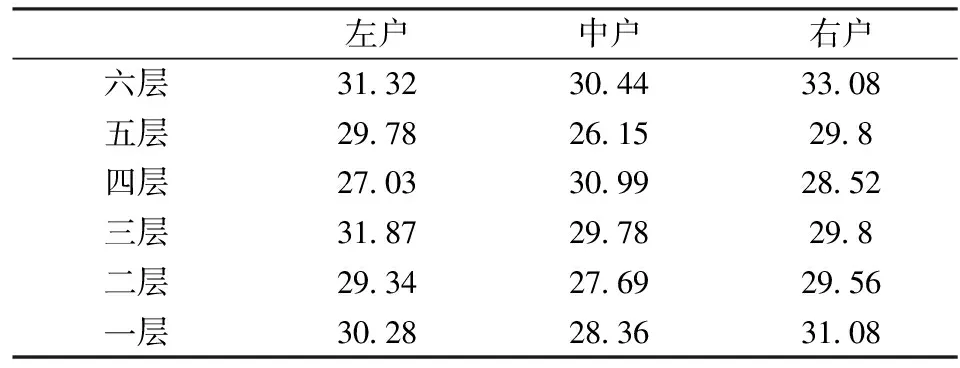
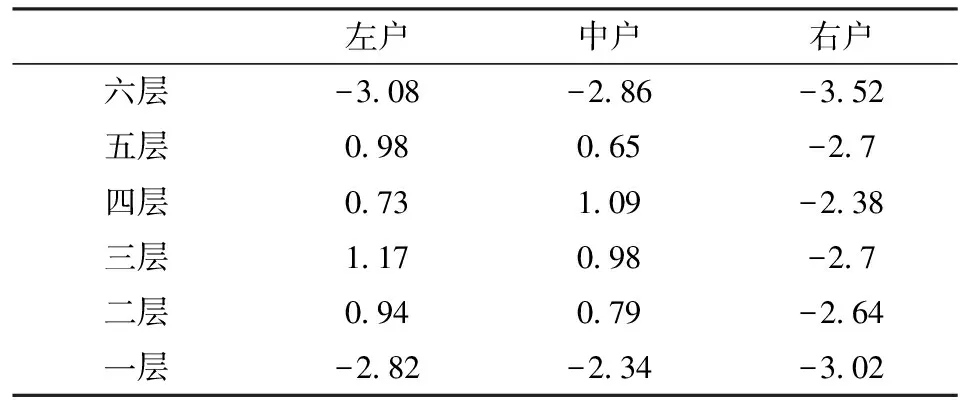
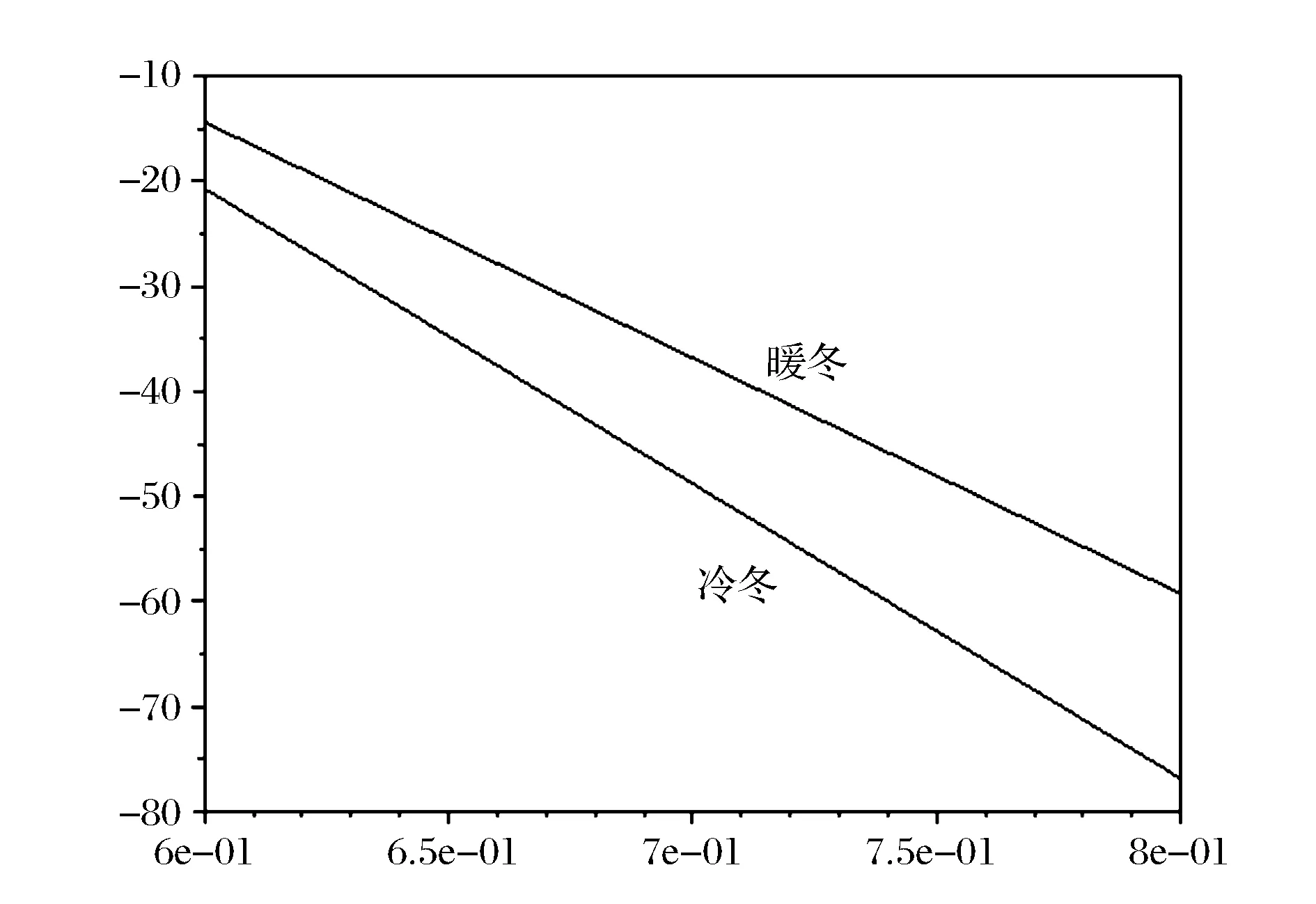
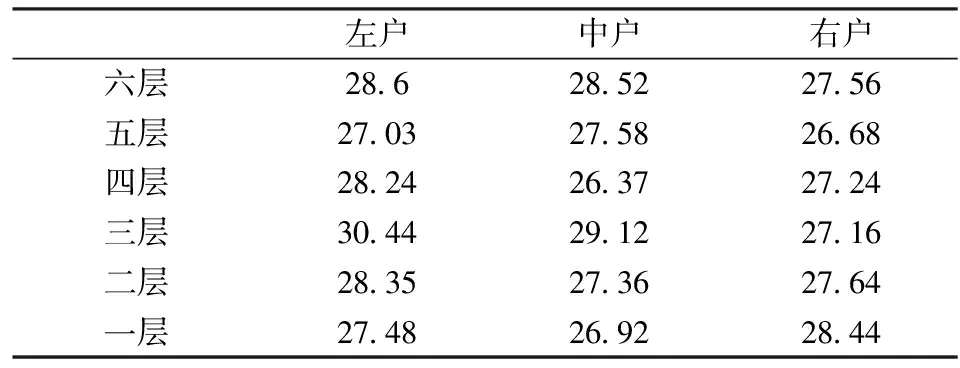
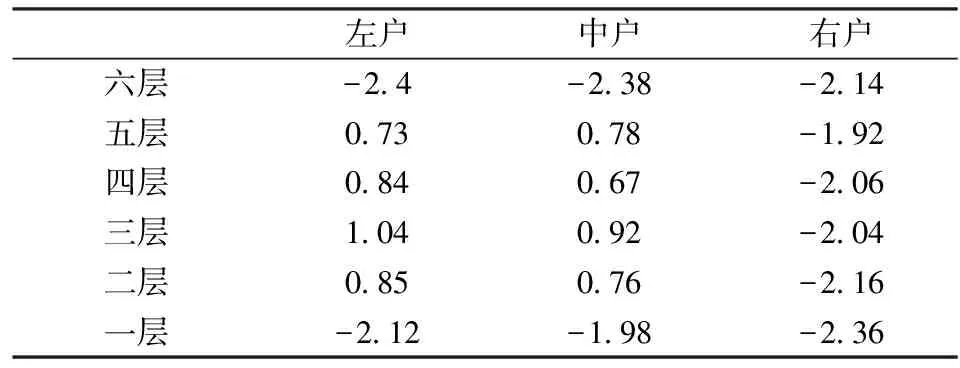
gi=aixi,0 (1) 耗散系数ai和吸热系数bi与建筑本身有关,给定一栋居民建筑,不做保温改造的前提下,ai和bi是固定值,0 px价格由供热单位通过成本测算给定。pg的价格未知,但可以通过其它变量表示。 按照理论上的热费计算方式,i住户采暖所花费的总费用是固定费用与采暖季用热量费用之和,即: Mi=D+pxxi (2) i住户实际享受到的热能为散热器散发的热量除去对外耗散的热量外加吸收邻居的传热量。 xi-gi+biGi (3) 用户的实际热费: (4) 3.3用户与邻居用热博弈 考虑一栋民用建筑内边角住户i和与其相邻的中间住户j的用热博弈(住户j泛指与i住户相邻的住户集合)。与公共物品私人自愿共享不同的是,热传递不能人为阻止,即住户只能减少公共品的提供(通过减少散热量来实现),但不能不提供公共品。即从用热成本偏好考虑,每个住户对公共热的供给有个下限。为简化起见,博弈分析过程中考虑以下三项假设前提。 (1)只考虑住户对自然界的热量耗散,不考虑从自然界吸收的热能。 (2)边角住户采暖季平均温度低于中间住户。 (3)住户之间并不知道各自的用热习惯和偏好。 基于上述假设,在本博弈中的公共物品是指由某一住户散热器散出,传递给其它住户或自然界的热量。其中向自然界的散热用于维持整个建筑内的热能平衡;户间传热使得“搭便车”行为始终存在。 图2 两住户用热示意图 考虑两用热住户情景下(边角住户i和中间住户j),总供给G=gi+gj,i住户和j住户进行不完全信息非合作博弈,即每个博弈的参与人独自要在满足自身基本用热生活的前提下,决定提供多少公共热,则i住户的决策问题可以表示为: maxU(xi,gi+gi) i住户公共热的最优供给量为: (5) 假设对G的供给是符合严格凸性的,gi*可以通过(5)的一阶导数获得。对住户i而言,公共热的供给结果为: G=max{gi*,gj} gi={gi*-gj,gi*} (6) 显然GI与Gi成反比,即当邻居对i住户传递的热量越多,i住户愿意提供的公共热就越少。在两住户的情况下,gj=Gi,因此,当j住户提供的公共热足够时,i住户愿意提供的公共热是满足其基本生活需求热能所散发的gi-。 i住户的反应函数为 在实际的热计量建筑中,基本上gi*>gj*,即边角住户比中间住户有着更高的公共热的供给要求(维系建筑与自然界的热耗散),边角住户更喜欢从中间住户传递的私人公共热。绘制反映曲线如图3所示。 图3 两住户用热博弈反应曲线图 上述博弈过程是在充分考虑用热成本的前提下开展的理论分析。实际上,由于信息不共享,很少有住户会按照下限来用热,因此公共热的供给是存在过剩现象的,这种过剩提高了整楼住户的舒适度,但在热计量计费过程中必须考虑对舒适度提升的边角住户的补偿。 3.4中间住户对边角住户的补偿 考虑到实际条件下,住户室温大多位于某一相对较窄的温度区间([16, 26]度区间)内,此区间内温度的增加和效用的增长近似保持线性关系。因此可以假设i住户的效用函数为齐次的科布-道格拉斯函数的形式。 (7) 0<αi,βi<1;0<αi+βi<1 即用户i的效用Ui与其计量用热量xi和邻居对用户i的传热量成正比。当用户的用热量增大,邻居的传热量也增加时,用户的效用才能提高。根据3.3中博弈分析,最大化i住户的效用函数,引入拉格朗日乘子,将费用约束(4)及耗散公式(1)代入效用函数中,计算纳什均衡解。 maxU(xi,Gi)+λ[Mi-D-px(xi-gi)-pgbiGi] (8) (9) (10) 根据纳什均衡,该模型的均衡条件为: (11) 代入科布道格拉斯形式的效用函数,得到: (12) 由此可得私有热价px和公共热价pg的比例关系: (13) (14) 和公共品私人自愿共享不同之处在于,当邻居散热量增加时,i住户自身散热量也会增加,即邻居通过散热满足了i住户的舒适度需求,i住户只需增加较少的成本就能提升自身舒适度,因此 3.5补偿分析 根据3.2的博弈分析,边角住户对公共热Gi的需求更多,相应地其α<β<1;中间住户更多依赖私有热,β<α<1;这两种热量决定了住户采暖季的室温,至于哪部分热量来自于自家散热器,哪部分热量来自于户间传热本身并无差别。 图4 耗散系数与热费变动关系图 供热计量试验最先在北京试点了8个小区,本文选择其中一个小区的某一板楼单元进行模拟试验,所有住户面积近似相等,数据采样从一楼(底层)到六楼(顶层),右侧把边,左侧住户与其他单元相连。固定费用按19元/m2(燃煤供热固定成本)计算。下面采用Scilab软件,模拟效用函数参数和耗散系数变化以及总费用变化对住户产生的影响。 表1 主要参数表 4.1效用函数参数变化模拟 对于边角住户,α的波动范围[0.3,0.5],对应的参数β的波动范围是从0.7至0.5的递减变动。以0.01为步长,固定耗散系数ai,中间住户为0.6,边角住户为0.45,模拟效用函数参数变动对边角住户和中间住户所带来的影响。 图5 固定耗散系数边角住户和中间住户费用变动 图5的横轴是边角住户参数α和中间住户参数β(二者变动范围相同)的叠加。从图5可以看出,边角住户总费用变动随着对私有热依赖的增加而减少,中间住户总费用变动随着对公共热依赖的增加而增加,二者的平衡点在0.42处,即当边角住户α=0.42,中间住户β=0.42时,边角和中间住户总体的收退费差异相等,在此位置最有利于平衡热用户之间的差异,提高热计量的推广程度。住户适当改变自己的效用函数,达到该点可以形成最有的博弈均衡;政府和企业对建筑设计与维护保温改造也有助于住户间达到均衡点。下面对于不同的建筑结构,耗散系数变化时各项参数的变化规律。 图6 耗散系数变动对住户费用变动的影响 图6中边角住户耗散系数从0.6-0.7变动,中间住户从0.4-0.5变动时费用变动曲线。可以看出,随着耗散系数的增加,边角住户和中间住户的费用变动整体下移(减少),可以理解为公共热的增加均衡了户间的热量差异,使得总费用降低。三个平衡点分别位于0.36、0.38和0.4处,即耗散系数的增加,使得住户间达到均衡时对私有热的依赖更少,公共热的依赖增加。若通过维护保温改造,进一步减少对自然界耗散的公共热,使得户间传递的公共热进一步增加,可以更多地降低总热费,因此建筑的外墙保温改造对于热计量的大面积推广非常有必要。 4.2不同气候条件下总费用变化 表2是该单元在冷冬采暖季单位面积的理论费用,表3是暖冬采暖季单位面积的理论费用。从成本最小的角度出发,在冷冬采暖季,整体室温偏低,居民用热量加大,散热量也增加,费用相应地上升,此时中间住户提供的公共热无法满足边角用户对外保温的需求;而在暖冬时期,中间住户提供的热量能够满足需求。下面根据表2和表3的实测数据,分别考虑冷冬和暖冬两种情景下的热费补偿。 表2 冷冬采暖季某热计量单元单位面积热费 (单位:元/m2,下同) 表3 暖冬采暖季某热计量单元单位面积热费 情景1:冷冬气象条件下,可以看出住户的热费普遍偏高。按照理论费用计算的边角住户费用相对中间住户差距很大,根据热费修正公式,计算得到调整后的单位面积热费为。 费用差异如表5所示。 可见调整后边角住户单位面积热费平均减少了2~3元/m2,中间住户增加1元/m2左右,中和了边角和中间住户的差异,有利于热计量的推广。就整个单元而言,其总热费减少了20.73元/m2,相当于供热企业调整后会减少效益,对于这部分费用而言,在热计量推广初期,可以考虑由政府补贴,以加快热计量拓展规模,降低综合成本。 表4 调整后冷冬某热计量单元单位面积热费 表5 冷冬调整前后费用差异 不同的热计量方式,耗散系数不同。模拟当边角住户散热系数在0.6~0.8变化时,该单元总热费变化情况,如图7所示。 图7 冷冬和暖冬条件下总热费与散热系数关系 从图7可以看出,边角住户散热系数越大,对整栋单元的实际费用与理论值的差距就越大。政府应根据热计量方式的不同,调整补贴的数量和比例。 情景2:暖冬气象条件下,住户的热费相对与冷冬较低,相应地边角和中间住户的差距也比冷冬时候低,但仍然存在边角住户公共品提供较多,需要补偿的情况。补偿后单位面积热费为: 表6 调整后暖冬某热计量单元单位面积热费 与调整前的费用差异如表7所示。 表7 冷冬调整前后费用差异 可以看出,边角住户在暖冬的补偿处于2元/m2左右,中间住户的缴费处于1元/m2以下。整体差距缩小,但总热费也相应地减少了14.97元/m2。这部分费用相对冷冬而言已经减少了,但为了推广热计量工作,最好仍有政府补贴企业这部分成本。 图5中暖冬条件下整体费用差距要比冷冬要小,而且随着边角住户耗散系数的增大,这种差距越来越大。可见气候的变化和热计量方式的选择对于供热企业运行成本影响很大,政府应根据当年实情,适时调整补贴政策。 通过上述分析可以看出, (1)减少不同位置住户收退费的差异必然会造成供热企业效益的降低,采暖季天气越冷这种效益降低程度就越明显。在冷冬气象条件下,供热企业应该考虑预先增加住户缴费的费用,以平衡暖冬和冷冬的差异。 (2)虽然冷冬条件下边角住户实际热费计算可以比理论值减少,但由于整体能耗的提升,使得这种费用减少不足以抵消目前热计量计费远远大于以前按面积计费(边角住户)的影响,费用差距虽然减少但整体费用上浮也是阻碍热计量推广的关键因素,因此需要设计额外的补偿机制以应对这种极端气候条件下的热计量成本提升的问题。 分户供热计量是北方采暖地区有效的建筑节能手段,作为一个新生事物,在推广过程中必然存在着保温改造、户间传热、压力波动、退费机制等影响热计量推广的新问题,这些问题大多涉及到政府、企业和热用户三者之间以及内部之间的利益博弈,需要必须通过深入的博弈分析研究,找到其中的突破口,制定相应的政策才能充分发挥热计量对节能减排所带来的效用。本文针对户间传热这一典型的问题,将户间传递热量看作住户的“公共物品”,通过相邻住户间对这种“公共物品”使用的博弈分析,得到了考虑户间传热这一核心影响因素的热费计算模型,并通过住户效用函数的参数模拟找到均衡点,实证分析表明,针对实际热计量建筑中存在的边角住户温度低、用热大,中间住户温度高、用热少的不足,模型有效地降低了住户收退费的差异,提高了热计量工作推广的力度,能够正确地的引导企业提升建筑质量,提高保温效能;推动居民开展行为节能,合理用热;促进政府制定针对性的政策措施,实现节能降耗。 目前博弈研究中仍以成本为居民考虑的优先要素,但实际上由于受到长期按面积供热缴费的影响,住户首先满足的是自身的用热舒适度,因此本文的博弈研究还适合于供热企业估算最低热计量使用成本。考虑到在热计量推广初期,居民在对热计量的认识和使用上都会存在误区,仅靠我们提出的热费计算模型可能还不足以激励居民进行供热计量改造的积极性。因此在政策制定方面,推广初期应对供热企业提供相应补贴政策,特别是在极端气象条件下提供额外补偿,以弥补热计量推广初期带来的企业规模报酬不高、热量耗散大的损失,待热计量面积扩大、居民对热计量的认知更理性后,供热企业运行成本会逐渐降低,此时再考虑逐步退出相关补贴政策,使热计量工作逐步进入到良性发展阶段。 [1] 黄维.“后计量”时代需要考虑的若干技术问题[J]. 暖通空调, 2011, 41(1): 71-73. [2] 徐伟, 宋波, 柳松,等. 我国供热计量技术支撑体系[J]. 建设科技, 2012,(18): 20-25. [3] 江亿. 北方采暖地区既有建筑节能改造问题研究[J]. 中国能源, 2011, 33(9): 6-13. [4] Fehr E, Schmidt K M. A theory of fairness, competition and cooperation[J]. Quarterly Journal of Economics, 1999, 114(3):817-868. [5] Rabin M. Incorporating fairness into game theory and economics[J]. American Economics Review, 1993, 83(5): 1291-1302. [6] Arrow K J,Colombatto E,Perlman M.The rational foundations of economic behavior[C]//Proceedings of the IEA Conference,Turin,Italy,1996. [7] Rabin M. A perspective on psychology and economics[J]. European Economic Review. 2002, 46(4-5): 657-685. [8] De Marco, G Morgan J. Slightly altruistic equilibria[J]. Journal of Optimization Theory and Applications, 2008, 137(2):347-363. [9] 蒲勇健, 杨哲. 轻微利他弱Pareto-Nash均衡[J]. 系统科学与数学, 2010, 30(9): 1259-1266. [10] Samuelson P. The pure theory of public expenditure[J]. The Review of Economics and Statistics, 1954, 36(4): 387-389. [11] Bergstrom T. On the private provision of Public Goods[J]. Journal of Public Economics, 1986, 29:25-49. [12] [美]丹尼斯大林C 穆勒. 公共选择理论[M]. 杨春学,译.北京: 中国社会科学出版社, 2010. [13] 石军伟,胡立君.企业社会资本的自愿供给:一个静态博弈模型[J].数量经济技术经济研究,2005,22(8):16-24. [14] 侯光明,李存金.管理非合作博弈机制式表述[J].中国管理科学,2002,10(3):86-90. [15] 陈潭.集体行动的困境:理论阐释与实证分析—非合作博弈下的公共管理危机及其克服[J].中国软科学,2003,(9):139-144. [16] 淮建军,刘新梅,雷红梅,等.地方政府和房地产商非合作讨价还价的博弈分析[J].运筹与管理,2008,17(3):70-74. [17] 吴云,周青.团队冲突的非合作博弈分析[J].科技管理研究,2012,32(23):143-146. [18] 张斌,华中生.供应链质量管理中抽样检验决策的非合作博弈分析[J].中国管理科学,2006,14(3):27-31 [19] 刘军,李成金.产量-价格策略下的双寡头动态多维博弈[J].中国管理科学,2008,16(6):150-155. [20] 刘洋,梁经锐.公共物品私人供给的纳什均衡分析[J].运筹与管理,2001,10(3):83-88. [21] 张荣,张宗益.电力竞价博弈中的信息结构[J].系统工程理论与实践,2013,33(1):92-98. [22] 卞亦文.非合作博弈两阶段生产系统的环境效率评价[J].管理科学学报,2012,15(7):11-19. [23] 张国兴,张绪涛,程素杰,等.节能减排补贴政策下的企业与政府信号博弈模型[J].中国管理科学,2013,21(4):129-136. [24] 李洪砚, 朱绪格, 张大鹏,等. 民用建筑“热改困局”:一个三方博弈的视角[J]. 价值工程, 2013, (35):113-115. [25] 金占勇, 武涌, 刘长滨,等. 基于外部性分析的北方供暖地区既有居住建筑节能改造经济激励政策设计[J]. 暖通空调, 2007, 37(9): 14-19. [26] 柴沁虎, 丁艳军, 袁伟亮,等. 不同供热收费模式的经济学分析[J].暖通空调, 2006, 36(10): 39-41. Research on the Game process Between Heat Consumers in Civil Building with Heat Metering ZHAOYu1,CHENRui1,3,LIAOYuan2,3 (1.National Academy of Innovation Strategy, Chinese Association for Science and Technology, Beijing 100863,China; 2.Institute of Science and Development, Chinese Academy of Sciences, Beijing 100190,China; 3.University of the Chinese Academy of Sciences, Beijing 100049,China) China has a large variety of existing and new apartment buildings which means its energy consumption grows faster with the increase of urbanization. Building energy consumption takes a large share of the total energy consumption. Reducing this part plays a key role in energy conservation and emissions reduction, which can be realized mainly by heat metering in consumers. Different with the other heat metering and allocation method which usually allocating the heat charge by building or neighborhoods, an allocation model between one user and its neighbors is constructed, linked with the heat transfer which can be considered as a game model. Usually most of these problems involved games among the government, the heat company and the residents. In this paper, the heat transferred between apartment is considered as a public goods. Followed the famous game problem of private goods sharing voluntarily, one resident which position is at corner and its neighbors in the center position are the two agents in this game. The Nash equilibrium is calculated, where the corner resident need more public heat than the center residents. When assuming the Cobb-Douglas utility function, A brand new heat allocation model is proposed which against the backdrop of low quality of heating building, deficiency of heat charging mechanism. Sharing the charge among the heat user and its neighbors, this model can more accurately measure the heat used during the heating season. Heat transfer between apartments, different heat use habits etc. can be solved and balanced the different locations of the user’s heat charge variation, which promote the large area heat metering work. The key is public heat and private heat prices of radiator heating and neighbor heat transfer are defied and used to construct the heat usage game model. The empirical research indicates that this model can availably handle many problems in the period of heat metering promotion, such as corner room, heat transfer between neighbors, different climate conditions etc., which gives citizen a new method and measure for utilizing and metering heat, promoting the energy conservation and emission reduction. heat metering; heat transfer between apartments; public goods; game theory 1003-207(2017)06-0169-10 10.16381/j.cnki.issn1003-207x.2017.06.018 2015-01-03; :2015-12-30 国家公益性行业科研专项(201310118);中国科学院科技政策与管理科学研究所重大研究专项B类(Y201161Z04) 陈锐(1975-),男(土家族),湖南张家界人,中国科协创新战略研究院副院长,研究员,研究方向:创新战略评估、宏观科技管理、城市运行与区域管理,E-mail:chenrui@cast.org.cn. F224 :A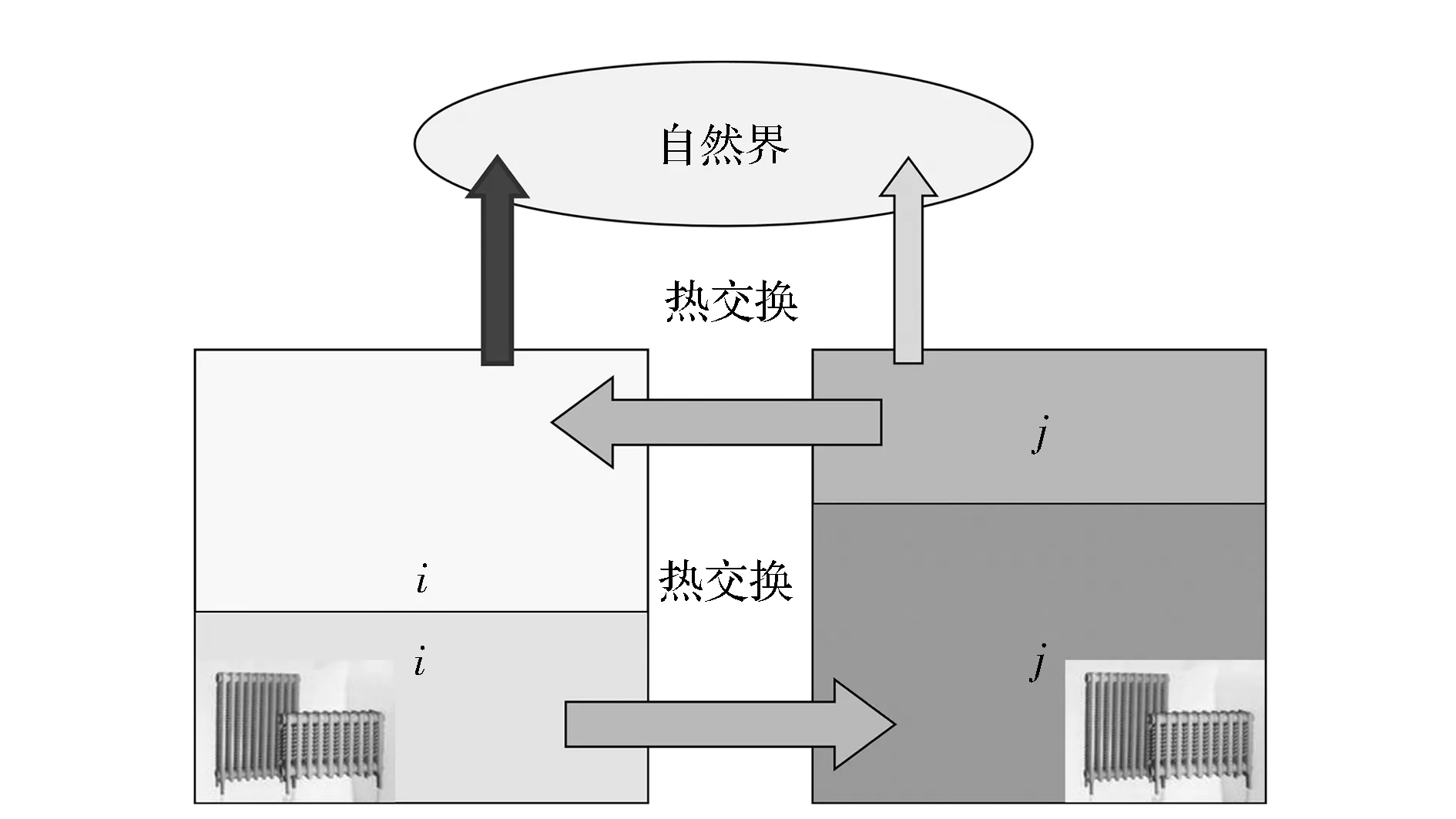
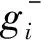
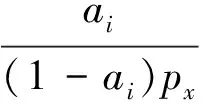
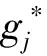
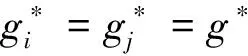
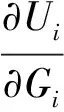
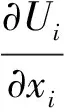
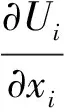
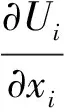
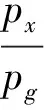
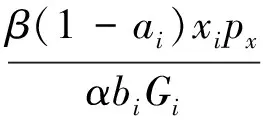
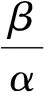
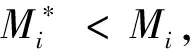
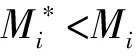
4 实证研究

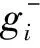
5 结语
