基于三次指数平滑模型的雾霾天气预测

李慧敏

（华北水利水电大学数学与信息科学学院，河南郑州450046）

基于三次指数平滑模型的雾霾天气预测

李慧敏

（华北水利水电大学数学与信息科学学院，河南郑州450046）

通过分析郑州市2013—2016年空气质量指数月统计数据，可以看出空气质量指数(AQI)、PM2.5、SO2等指标均关于时间呈非线性趋势。应用三次指数平滑模型对郑州市2017年每月的AQI、PM2.5、SO2等指标进行预测。结果表明，郑州市2017年雾霾天气与实际季节变化相符，且呈“U”型分布。

雾霾；大气污染；空气质量；指数平滑法；预测模型

雾霾主要由二氧化硫、氮氧化物和可吸入颗粒物组成，前两者为气态污染物，最后一项颗粒物才是加重雾霾天气污染的罪魁祸首。颗粒物的英文缩写为PM，人们通常所说的PM2.5，就是指大气中直径≤2.5 μm的颗粒物[1]。雾霾天气作为一种重要的城市气象灾害并不是一蹴而就的，而是很多因素的综合导致了雾霾的产生。近年来，雾霾这一现象在英国、美国、日本、德国、法国等多个经济发达的国家一度暴发并造成严重影响。除此之外，我国中东部地区也多次出现了大范围的持续雾霾天气[2]，给人们生产生活造成了严重影响，危害了社会公众的正常生产生活，雾霾天气已经成为我国重要的环境公害[3]。准确地预测雾霾程度，对提前做好防护措施，降低其对人们生产生活造成的危害有着极为重要的意义。

郑州是我国雾霾多发区和重灾区，针对此现象，大多国内外学者仅仅是分析了雾霾出现的原因以及雾霾现象对人们生产生活等造成的影响，并没有对此现象作出合理的预测[4-6]，为有效控制郑州雾霾现象的出现及提前做好防护工作，有必要对该地区雾霾天气进行分析与预测。本研究以中国空气质量在线监测分析平台发布的郑州2013—2016年空气质量指数为参考[7]，以PM2.5、SO2、CO等大气污染物浓度数据作为依据，然后通过折线图对这些因素进行初步分析并建立三次指数平滑模型，对郑州2017年的空气质量进行预测。

2012年2月国务院发布空气质量新标准《环境空气质量标准》（GB3095—2012）规定：“当大气成分中PM2.5日均浓度大于75 μg/m3时，可作为判断雾霾的重要标准”[8]。本研究雾霾判断标准为PM2.5月均浓度大于75 μg/m3，空气质量指数AQI月均浓度大于100 μg/m3。

1 指数平滑预测模型

1.1 模型简介[9]

三次指数平滑法模型如下：

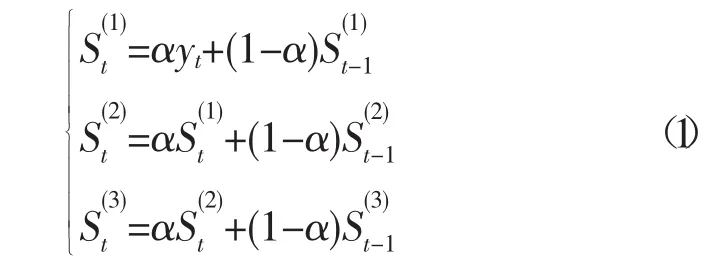
三次指数平滑的预测模型为：

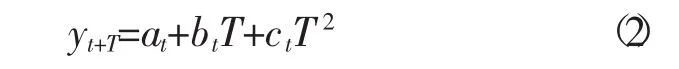
式中：yt+T是预测值，T为需要预测值的时间序列与目前序列的间隔数。

平滑系数公式为：

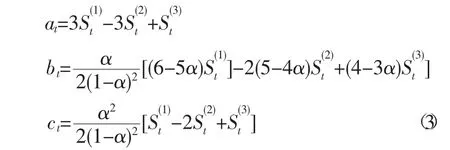
1.2 初始值的选择[10]

当时间序列数据项数较多时（N≥15），可以选用第一期的观察值作为初始值；原数列项数较少时（N≤15），可以选取最初几期（一般为前三期）的平均值作为初始值。

1.3 平滑系数α的选择[11]

用指数平滑法计算的关键是确定α的大小，由于α的取值容易受主观影响，因此合理确定α的取值十分重要。一般来说，如果数据波动较大，α值应取大一些，这样可以增加近期数据对预测结果的影响。如果数据波动平稳，α值应取小一些。另外，试算法也是经常用到的一种方法，其基本判断依据是均方误差（MSE）最小。

2 预测模型的建立与应用

2.1 模型选定

利用Matlab画出郑州市2013—2016年共48个月关于空气质量指数（AQI）、PM2.5含量、SO2含量以及每月空气质量达标天数变化趋势，如下图所示。

由图1可知，四组空气质量指标数据均呈非线性趋势，因此建立三次指数平滑模型进行分析和预测，另外考虑到气候的季节性，在预测时将数据共分为12组，每组数据分别取自于不同年的同一月份，并用这些数据来预测下一年相对应的值。

2.2 参数的选择

本研究最初预测数据为四项，该模型初始值为四项的均值。对于平滑系数α的选择，采用试算法并根据选取均方误差（MSE）最小的原则来确定，其公式为：

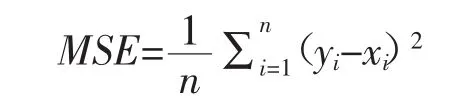
式中n为原始数据的个数，yi为第i序列对应的预测值，xi为第i序列对应的原始实际值。

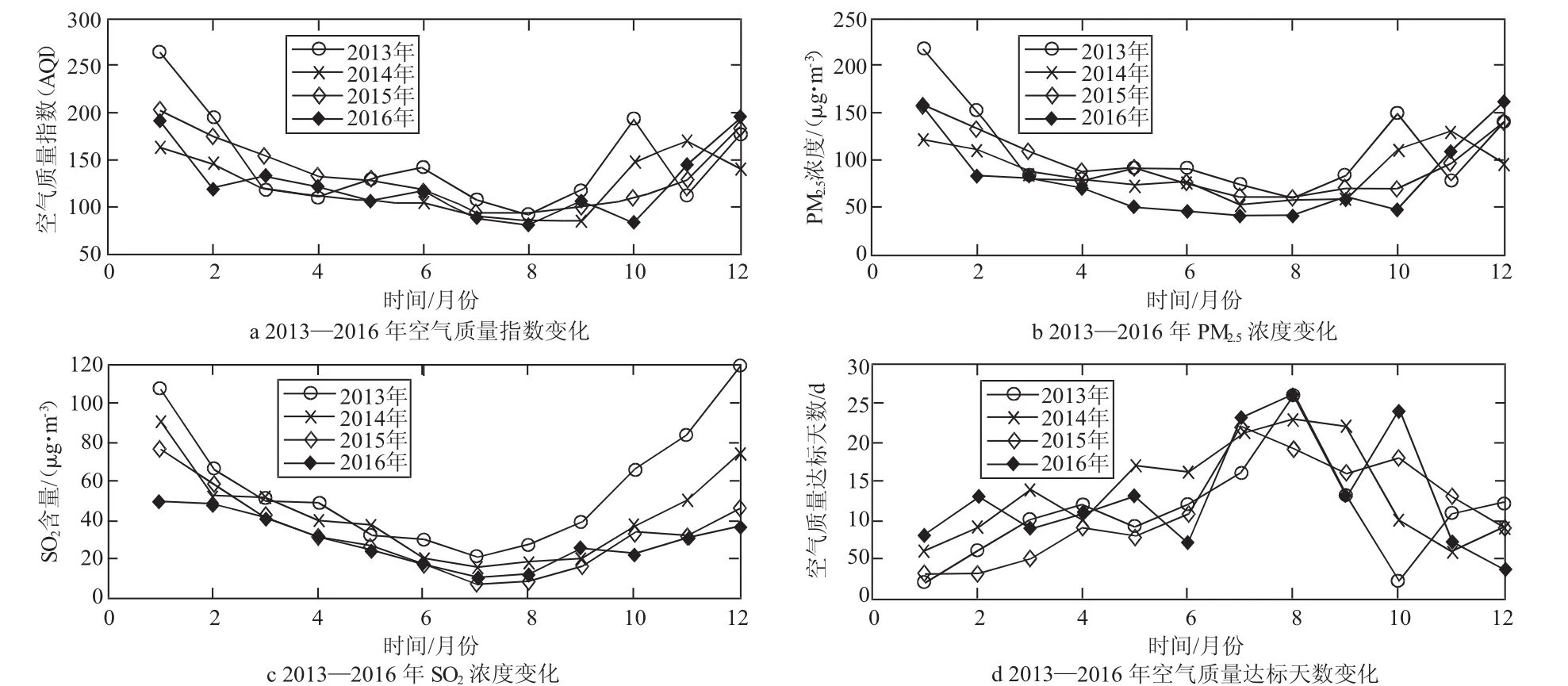
图1 2013—2016年空气质量指标变化趋势

2.3模型预测结果

按上述方法，最后分别确定AQI、PM2.5、SO2以及每月空气质量达标天数的α值，将确定了的值代入（2）、（3）式即可对郑州未来一年的AQI、PM2.5、SO2以及每月空气质量达标天数进行预测。下面仅列出AQI预测结果，如表1所示。

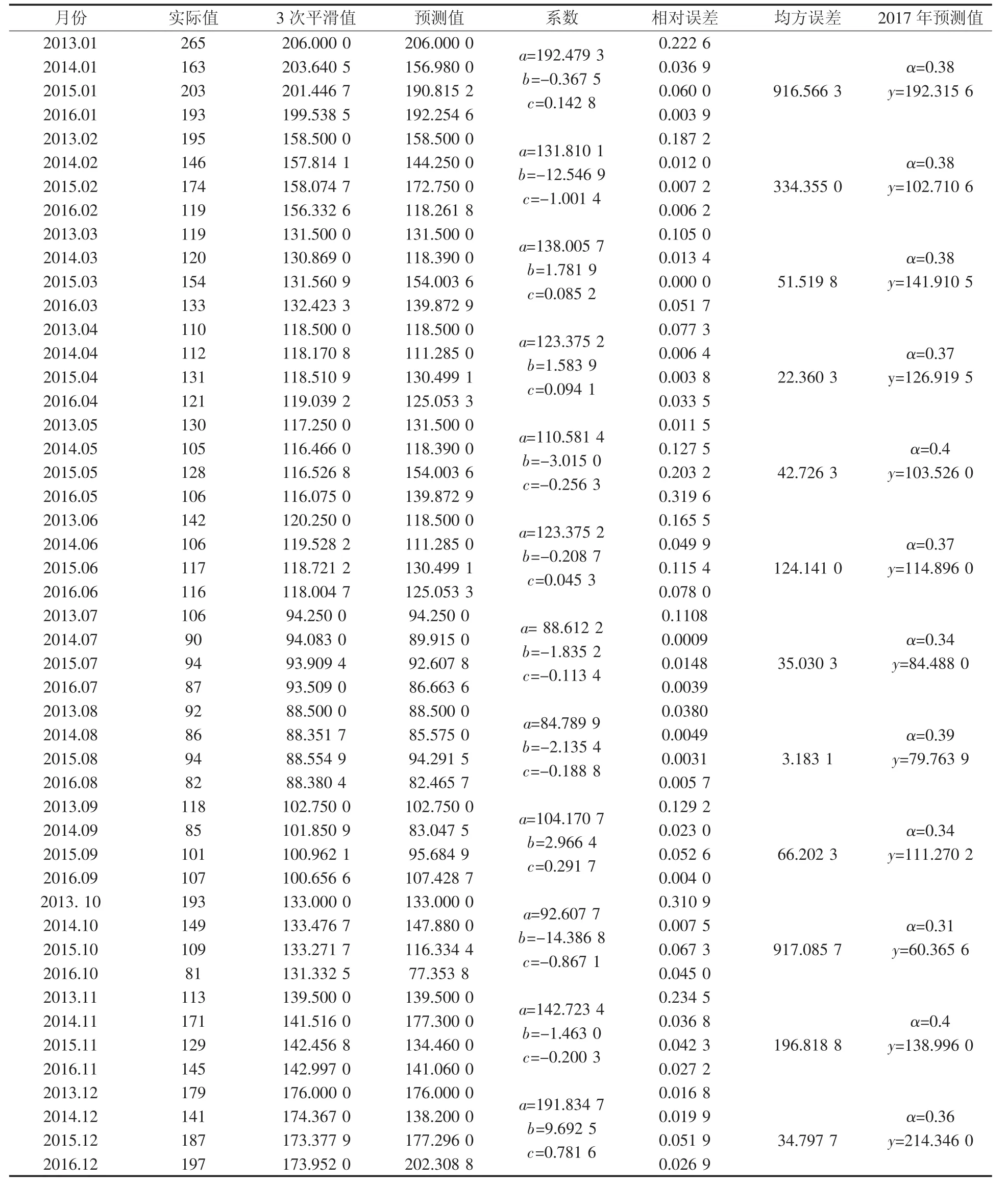
表1 AQI三次指数平滑预测结果

经过实际值与预测值的对比，发现模型对空气污染指数能够进行大致预测，模型检验通过则该预测模型适用于对雾霾天气的预测。用类似的方法分别对PM2.5、SO2、天气质量达标天数进行预测，预测结果如表2所示。

下面用折线图表示2017年预测结果，如图2所示。

从图2可见，郑州市2017年空气质量指数AQI与PM2.5、SO2是同步变化的，其中7月、8月、9月、10月空气质量较好，1月、3月、11月、12月空气质量较差。这与历史空气质量趋势相符，可见预测方法有效。

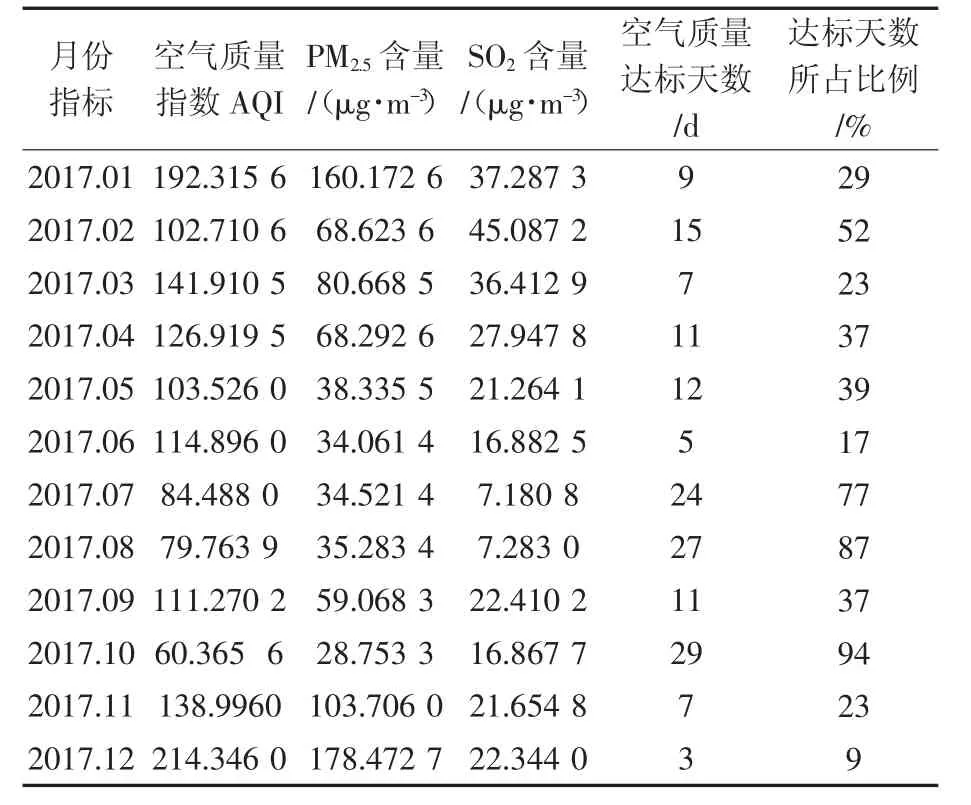
表2 利用Matlab编程求得2017年空气质量各指标的预测值

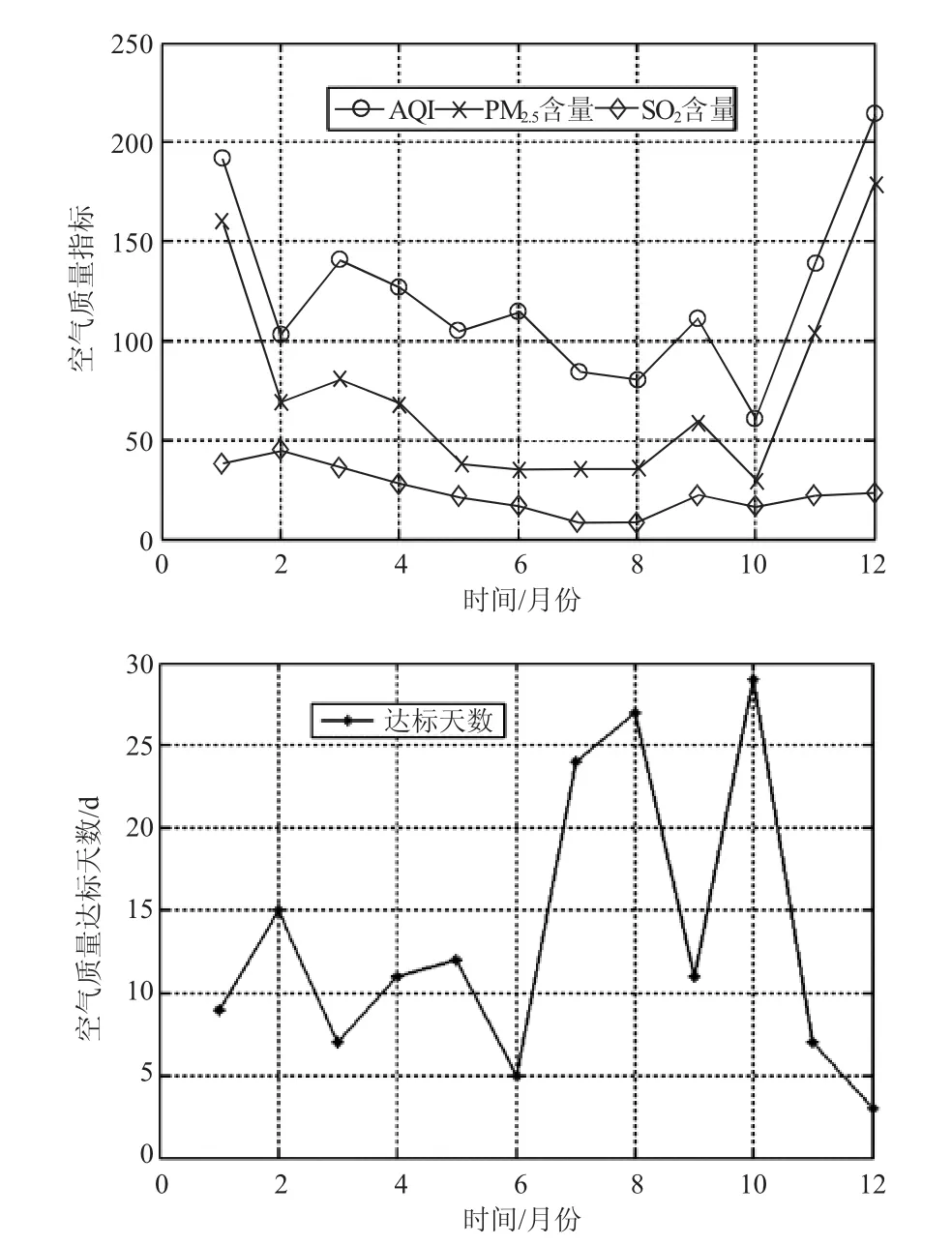
图2 2017年空气质量各指标趋势

3 结论

通过观测2013—2016年郑州市空气质量指标趋势图，并结合三次指数平滑模型对各指标的预测结果综合分析，得到如下结论：

（1）郑州市2017年雾霾天气仍呈“U”型分布，其中1月、3月、11月、12月空气质量达标天数较少，尤其12月份最少。这说明在污染排放相对稳定的前提下，郑州市空气质量冬季最差，雾霾天数最多，春季略低，秋季次之，夏季所占比例最低，雾霾天数也最少。其中，秋末冬初（11月至翌年1月）是雾霾高发季节，这是大气污染物和季节变化综合作用的结果。

（2）对郑州市雾霾天气的预测对人们实际生产生活具有一定的指导意义。由预测结果以及对往年郑州市空气质量的分析可知，尤其在冬季，人们特别需要做好环境空气质量预警工作以及对雾霾天气的防护工作。除此之外，在出现连续重度污染时要结合当时气象条件，及时采取包括限产、限行等措施，有效改善空气质量，防止对人体造成更大损害。

（3）2013—2016年郑州市空气质量指数月统计数据显示，郑州雾霾天气的污染指标均关于时间呈非线性趋势，故选用三次指数平滑模型对雾霾天气进行预测，其模型优势在于计算简便、精度较高且可以选取较少的数据作为初始值，因此利用4年郑州市空气质量指数月统计数据进行天气预测较为适用。但由于计算时运用试算法对于平滑系数α进行选择，故对于预测结果可能会存在一定的误差。

[1]侯琼煌，杨航.基于三次指数平滑模型的雾霾天气分析与预测[J].环境保护科学，2014，40（6）：73-77.

[2]ZONGWEI MA，XUEFEE HU，ANDREW M.SAYER，et al.Satellite-Based Spatiotemporal Trends in PM2.5Concentrations：China，2004—2013[J].Environmental Health Perspectives，2016，124（2）：184-192.

[3]TIE X，ZHANG Q，HE H，et al.A budget analysis of the formation of haze in Beijing[J].Atmospheric Environment，2015，100：25-36.

[4]杨洪斌，邹旭东，汪宏宇，等.大气环境中PM2.5的研究进展与展望[J].气象与环境学报，2012，28（3）：77-82.

[5]LIU Y，PACIOREK C J，KOUTRAKIS P.Estimating regional spatial and temporal variability of PM2.5concentrations using satellite data，meteorology，and land use information[J].Environmental Health Perspectives，2009，117（6）：886-92.

[6]梁磊，周莹.大气雾霾污染法律治理研究[J].中国环境管理干部学院学报，2015，25（4）：39-42.

[7]中国空气质量在线监测分析平台.2013年1月—2016年12月郑州空气质量指数月统计历史数据[EB/OL].https：//www.aqistudy.cn/historydata/sponsor.php

[8]HE K，YANG F，MA Y，et al.The characteristics of PM2.5，in Beijing，China[J].Atmospheric Environment，2001，35（29）：4959-4970.

[9]王坤龙.天津地区雾霾的成因及预测模型建立的研究[J].天津职业院校联合学报，2014，16（8）：25-29.

[10]方天舒.陕西雾霾天气预测[J].合作经济与科技，2016（11）：184-185.

[11]汪选胜.改进的三次指数平滑模型在交通优化中的研究与应用[J].机械制造与自动化，2012，41（4）：18-20.

（编辑：程俊）

Prediction of Haze Weather based on Cubic Exponential Smoothing Model

Li Huimin
（College of Mathematics and Information Science,North China University of Water Resources and Electric Power,Zhengzhou Henan 450046,China）

Through analyzing monthly data of Zhengzhou from 2013 to 2016,observed a nonlinear trend of the air quality indices such as AQI,PM2.5,SO2,etc.Therefore,the cubic exponential smoothing model was applied to forecast the monthly AQI,PM2.5,SO2of Zhengzhou in 2017.It showed that the appearance of the haze weather was consistent with the change of actual seasonal,and was distributed by"U"type in 2017.

haze,air pollution,air quality,cubic exponential smoothing model,prediction model

X511

A

1008-813X（2017）03-0052-05

10.13358 /j.issn.1008-813x.2017.03.14

2017-04-10

李慧敏（1992-），女，河南商丘人，华北水利水电大学数学与应用数学专业硕士研究生在读，主要从事金融数学的研究。