冰箱压缩机2自由度隔振系统动态分析与测试

王孚懋，宋 磊，张兰青，兰同宇，韦艳娟

（山东科技大学 机械电子工程学院，山东 青岛 266510）

冰箱压缩机2自由度隔振系统动态分析与测试

王孚懋，宋 磊，张兰青，兰同宇，韦艳娟

（山东科技大学 机械电子工程学院，山东 青岛 266510）

将某型号冰箱压缩机简化为一种2自由度隔振模型，考虑垂直与侧倾两种运动形态，应用拉格朗日法建立动力学方程，绘制参数变化的幅频响应曲线，分析弹簧刚度、支撑间距、偏心距和系统阻尼对力传递率的影响。通过模态实验法测得2阶固有频率，与理论计算值进行对比，验证了理论分析的可靠性，可为冰箱压缩机结构优化与减振降噪设计提供参考依据。

振动与波；冰箱压缩机；泵体隔振系统；振动测试

压缩机作为家用电冰箱的动力源和心脏，是冰箱振动与噪声的主要来源，也是减振降噪工程设计的主要目标[1]。压缩机振动与噪声主要来自曲轴活塞系统旋转与往复运动产生的不平衡力、运动构件的摩擦、阀片冲击升程限位器以及阀座[2]。冰箱压缩机动力学研究主要是力学模型简化、动力平衡、源特性识别与系统优化几个方面。例如，文献[3]运用子结构导纳法建立压缩机柔性基础双层隔振系统的传递率公式，通过参数优化，采用增大阻尼方案获得了理想隔振效果。

本文针对某型号冰箱压缩机减振降噪问题，建立了2自由度动力学模型，对压缩机隔振系统进行动态特性分析，分析了参数变化对力传递率的影响，通过模态实验法验证了理论分析的可靠性。

1 压缩机泵体动力学建模

以某型号冰箱压缩机为研究对象，这是一款单转子滚动活塞式压缩机，也称为全封闭往复式压缩机。运动部件及电机利用弹簧支撑方式密闭于一个封闭的壳体空间，压缩机运动部件产生的振动经由支撑弹簧和内排气管传递给壳体，使壳体振动并辐射噪声。除去压缩机上、下外壳后，主体结构如图1所示。主要由泵体1、内排气管2和支撑弹簧3等组成。

如图1所示，将压缩机泵体视为一个质量为m的刚性单质体，质心位于坐标O处。根据压缩机的结构和运动特性，视XOZ为对称面，考虑泵体沿Z轴

图1 压缩机主体结构组成

方向的垂直运动和绕Y轴的侧倾运动，将泵体隔振系统简化为两个自由度运动系统，质体绕Y轴的转动惯量为J。将两组支撑弹簧刚度等效为k1、k2，弹簧中心线（作用力）与质心水平距离分别为l1、l2。忽略内排气管的弹性约束和两组弹簧的质量，将连接管道的位移约束以及系统的能量损耗等效为阻尼器c。将泵体垂直方向作用力记为fz(t)，力的偏心距为e。由于泵体其它方向的运动很小，忽略水平方向弹性影响，得到如图2所示的压缩机泵体2自由度动力学模型。

图2 压缩机泵体二自由度力学模型

取广义坐标为z与θ，广义速度为ż与θ̇。采用复刚度K*=k(1+iη)来表示隔振器弹性，η为阻尼器c的损耗因子，k为弹簧的刚度系数[4]，应用拉格朗日方程，可得2自由度隔振模型的动力学方程为

应用克莱姆法则，求得q1与q2分别为

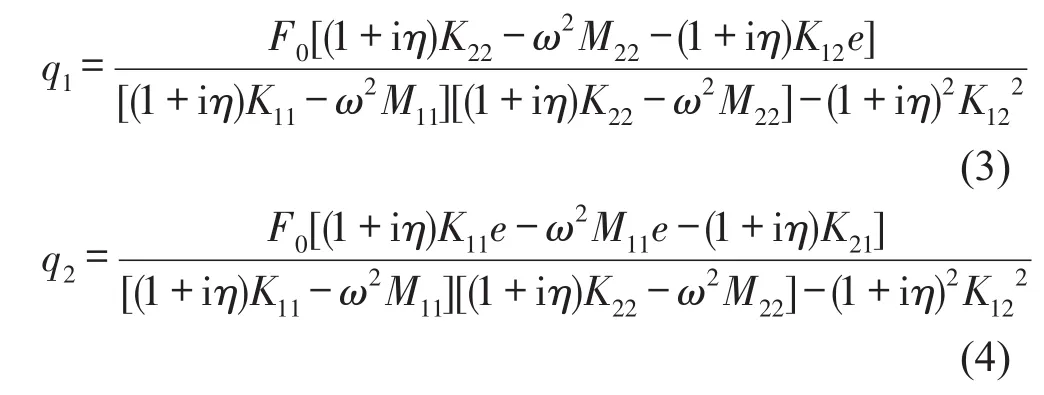
由此，得支撑弹簧k1和k2的位移幅值为

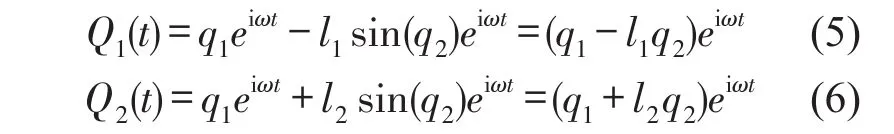
将式(3)、式(4)代入上式，可以得到

由式（2）得有阻尼自由振动特征矩阵方程

则无阻尼自由振动特征矩阵方程为

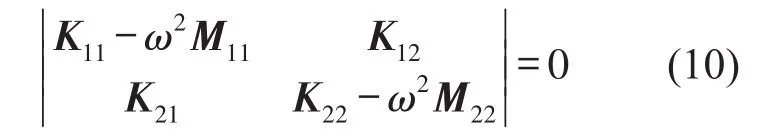
利用Matlab软件分别求得无阻尼和有阻尼2自由度自由振动系统的两个固有频率，如表1所示。

表1 2自由度隔振模型的固有频率

其中ω1是沿Z轴垂直运动固有频率，ω2是绕Y轴侧倾运动固有频率。有阻尼系统的固有振动角频率随着阻尼的增大而左移，本系统为小阻尼，阻尼对固有频率影响不明显。由于采用复刚度法模拟隔振器的阻抗，等效刚度发生了变化，固有频率计算结果略有偏差。冰箱压缩机额定转速为n=2 800 r/min，则工作频率ω=2πn/60=293.215 3 rad/s，介入固有频率ω1与ω2之间。

2 压缩机泵体隔振参数变化影响

由胡克定律F=k(x-x0)（刚性基础x0=0），经过支撑弹簧k1和k2，传递到基础上的力分别为：F1(t)=k1Q1(t)，F2(t)=k2Q2(t)，隔振器传递到基础上的合力为

隔振器支撑传递到基础上的合力幅值为

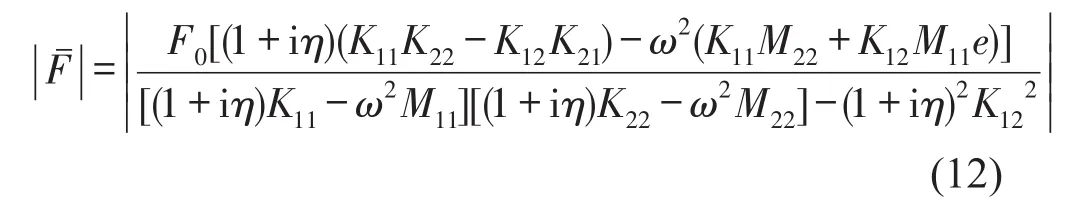
作用于泵体上的激振力通过支撑弹簧k1和k2传递到壳体上，传递力越小，系统隔振效果越好。将传递到壳体上的合力幅值与激振力幅值的比值定义为力传递率，即

由于力传递率的数值很小，取以10为底的对数，得到力传递率的对数表达式

由上式看出，影响隔振效率的主要因素为刚度、阻尼、支撑间距和偏心距[5]。

冰箱压缩机原始参数如表2所示。将工作频率ω=293.215 3 rad/s代入式(13)，得力传递率Tb= 5.76%。

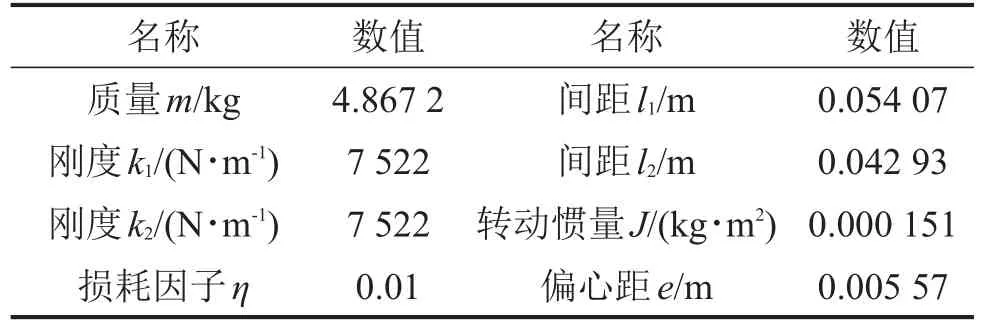
表2 压缩机2自由度隔振模型的物理参数

设系统单自由度固有频率为

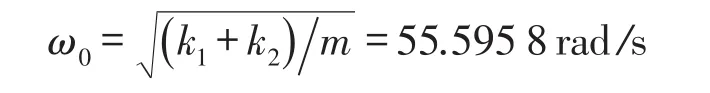
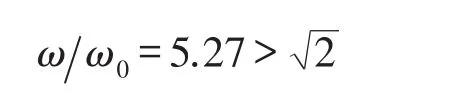
这是隔振设计的理论基础。以频率比r=ω/ω0为横坐标，绘制各参数变化对力传递率的影响曲线，如图3所示。

图3(a)是弹簧刚度对传递率的影响。两组弹簧刚度须在允许静变形范围内，分别取k1/k2=0.5、1、1.5。由曲线可知，k1＜k2时，系统第二个共振峰值左移，且在工频位置出现反共振点，传递率下降显著，有利于减振设计。k1＞k2时，传递率曲线整体右移，隔振效果较差。

图3(b)是支撑间距对传递率的影响。结构整体尺寸不变，分别取l1/l2=0.5、1.25、1.5。由曲线可知，l1＜l2时，系统第二个共振峰左移，且在工频位置出现反共振点，传递率下降明显。l1＞l2时，传递率曲线整体右移，隔振效果较差。

图3 隔振系统参数对力传递率的影响

图3(c)是激振力偏心距对传递率的影响。分别取e/e0=-1.5、1、1.5。由曲线看出，偏心距反向增大时，在工频位置出现反共振点，传递率下降明显，有利于隔振设计。

图3(d)是系统阻尼对传递率的影响。增大阻尼，工频传递率下降，两个共振峰值明显减小，即阻尼对共振有明显的抑制作用。

4 实验模态分析

利用LMS Test.Lab振动与测试系统中的锤击法对压缩机隔振系统进行振动模态实验测试[6]。在X、Y、Z轴三个方向上拾取压缩机2自由度隔振模型的振动响应频谱图，可以得到压缩机前2阶固有频率。

将压缩机2自由度隔振模型实验测试所得到的前2阶固有频率值与理论计算值作比较，如表3所示。

表3 固有频率的测量值与计算值对比

由表3中可以看出，沿Z轴垂直运动固有频率理论计算与试验测试值相差1.01%，绕Y轴侧倾运动固有频率理论计算与试验测试值相差2.29%，以上误差均在工程计算许可范围，证明2自由度隔振模型的计算结果是可靠的。

5 结语

本文将冰箱压缩机泵体简化为垂直与侧倾运动的2自由度隔振模型，通过模态实验分析，误差均在工程计算许可范围，验证了动力学理论模型的可靠性。

通过隔振力传递率计算与分析表明，减小刚度k1和增大刚度k2、减小间距l1和增大间距l2、反向增大偏心距和增大系统阻尼，工频传递率下降，有利于提高隔振效率，为系统优化设计提供了参考依据。

[1]李洪亮，黄协清，陈花铃.冰箱压缩机减振降噪的应用研究[J].机械科学与技术，2002，21(S)：9-10.

[2]王小龙，李志远，冯洋威，等.小型往复式压缩机配重优化设计与仿真和试验研究[J].机械设计，2016(1)：21-24.

[3]东志翔，黄协清，沈海波.冰箱压缩机支撑系统的动力学分析与优化[J].机械强度，2006，28(2)：205-210.

[4]黄其柏，宋朝，曹剑，等.基于复刚度法的浮筏隔振系统有限元分析[J].华中科技大学学报，2007，35(1)：99-101.

[5]王孚懋，杨龙，赵丽芳.水泵机组浮筏隔振系统研究[J].噪声与振动控制，2008，28(5)：36-39.

[6]郭维，刘斌，冯涛，等.冰箱压缩机机壳实验模态分析[J].噪声与振动控制，2010，30(3)：67-70.

DynamicAnalysis and Test of 2-DOFVibration Isolation System of a Refrigerator Compressor

WANG Fu-mao,SONG Lei,ZHANG Lan-qing,LAN Tong-yu,WEI Yan-juan
(College of Mechanical and Electronic Engineering,SUST,Qingdao 266510,Shandong China)

A refrigerator compressor is simplified to a 2-DOF vibration isolation model.Considering vertical and rolling movement patterns,the dynamic equation of the model is established based on Lagrange method.The amplitude-frequency response curves with parameter variation are plotted.The effects of spring stiffness,support spacing,eccentricity and system damping on the force transmissibility are analyzed.By means of the modal experiment method,the natural frequencies of the first two orders are measured and compared with the theoretical calculation results,and the reliability of the theoretical analysis is proved.This work provides a reference for structure optimization and vibration and noise reduction design of refrigerator compressors.

vibration and wave;refrigerator compressor;pump body vibration isolation system;vibration test

TB535

：A

：10.3969/j.issn.1006-1355.2017.03.018

1006-1355(2017)03-0092-04

2016-11-25

中国煤炭工

业协会科学技术研究项目资助（MTKJ2015-249）

王孚懋（1960－），男，山东省莱州市人，教授，研究方向为动力机械振动与噪声控制。

宋磊（1992－），男，在读硕士研究生。E-mail:wangfumao@sdust.edu.cn