AEO解调方法及在滚动轴承故障诊断中的应用

程军圣，向天尧，杨兴凯，杨 宇

（湖南大学汽车车身先进设计制造国家重点实验室，长沙410082）

AEO解调方法及在滚动轴承故障诊断中的应用

程军圣，向天尧，杨兴凯，杨 宇

（湖南大学汽车车身先进设计制造国家重点实验室，长沙410082）

针对希尔伯特变换与传统能量算子解调方法的缺点，提出一种新的解调方法——解析能量算子（Analytic Energy Operator，AEO）解调。仿真信号分析结果表明，相对于希尔伯特变换与传统能量算子解调，解析能量算子解调方法具有较高的解调精度。基于解析能量算子解调，又提出基于AEO能量谱的滚动轴承故障诊断方法，对滚动轴承仿真和实验信号进行分析，与其它方法的对比结果表明所提出方法的有效性和优越性。

振动与波；解调方法；解析能量算子；滚动轴承；故障诊断

当轴承发生故障时，其故障振动信号往往表现为调制形式，因此解调分析成为轴承故障诊断的一种常用的信号处理方法，在理论和实践方面都取得了许多研究成果，并得到了广泛的应用[2–3]。目前，轴承故障诊断中常用的方法是采用希尔伯特变换（Hilbert Transform，HT）对信号进行解调，从而提取振动信号的故障特征信息。但是HT在端点处有能量泄露，而且具有不可避免的加窗效应，使得解调结果往往出现非瞬时响应特性，即解调出的瞬时频率和瞬时幅值存在振荡，从而使解调误差增大[4]。同时，HT还受Bedrosian定理的限制，即单分量信号的包络信号和调频信号的频带不相交[5]。这些都限制了HT解调的应用。

能量算子（Teager Energy Operator，TEO）解调方法能有效提取轴承信号的瞬时幅值和瞬时频率信息[6]，研究结果表明，TEO的解调效果明显优于HT解调，同时计算量也大大降低[7–8]。然而，TEO在解调过程中存在误差项，包括低频误差分量和高频误差分量两部分。只有满足待解调信号的瞬时幅值和瞬时频率远远小于载波频率这一假设条件时，误差项才会较小，TEO才能取得较好的解调效果[9]。另外，TEO解调方法在频率准确度和信号波形度方面还不尽人意，瞬时频率和瞬时幅值在端点及突变点会产生较大的波动[10–11]。

本文在HT和TEO方法的基础上，提出了一种新的解调方法——解析能量算子（Analytic EnergyOperator，AEO）解调。利用解析能量算子在增强滚动轴承故障信号冲击成分方面的优势，由信号的AEO能量谱识别轴承的故障特征频率，从而分析故障原因。滚动轴承仿真和实验信号分析结果表明了该方法的有效性和优越性。

1 解析能量算子解调

1.1 解析能量算子

单分量的调幅调频(AM-FM)信号，其时变幅度和时变相位分别为a(t)和ϕ(t)，可以写成

其瞬时频率为

信号的解析形式为

其中sj(t)即为信号sr(t)的希尔伯特变换

对s(t)可定义非线性的解析能量算子

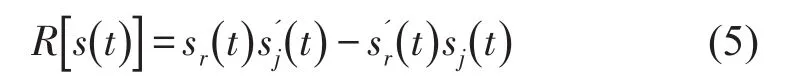
因此，可以得到AM-FM信号的解析能量算子为

1.2 解析能量算子的瞬时频率、瞬时幅值估计

解析能量算子的连续形式已经在公式（5）中定义，向后差分可得到其离散形式

本文利用解析能量算子的运算性质，对信号的瞬时频率和瞬时幅值进行了估计。对于离散的AMFM信号

式中n为离散采样时间点，a(n)为瞬时幅值，ϕ(n)为瞬时相位。瞬时角速度Ω(n)定义为ϕ(n)的向后差分

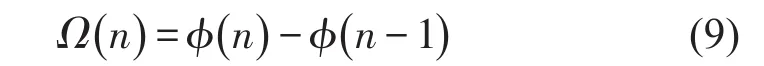
则AM-FM信号的离散形式为

AEO和TEO都是基于局部的微分运算，但后者在解调过程中存在误差项，包括低频误差分量和高频误差分量两部分，只有满足待解调信号的瞬时频率和瞬时幅值是近似常数或是缓慢变化的信号时，误差项才会较小，TEO才能取得较好的效果。然而并不是每一个单分量信号都满足这个条件，因此当信号瞬时频率或瞬时幅值变化较大时，TEO的估计结果会出现较大的偏差，甚至不能使用。而AEO则不存在上述误差项，在对单分量信号进行解调时，估计结果会更准确。

2 基于解析能量算子能量谱的滚动轴承故障诊断

2.1 方法原理

信号能量的定义一般为信号幅值的平方，只代表势能或动能。如果信号的冲击幅值较小，用它来跟踪信号的冲击瞬态特性的话，那么冲击成分很可能被其他成分淹没，而达不到效果。TEO的能量输出与AEO的能量输出形似，但与AEO相比少了低频误差分量和高频误差分量两部分[12]。因此在解调时，TEO会受到应用条件的限制，即待解调信号的瞬时幅值和瞬时频率远远小于载波频率。AEO的输出为瞬时幅值的平方和瞬时频率之积，它与传统的信号能量定义相比，多乘了瞬时频率。因为信号的瞬时频率较高，因此AEO更能跟踪信号的冲击瞬态特性。同时，由于AEO的能量输出没有误差项的干扰，不受TEO应用条件的限制，使AEO应用范围更广。

滚动轴承出现故障时，产生的周期性冲击频率能反映轴承的故障原因。本文根据这一原理，提出了基于解析能量算子谱分析的轴承故障诊断方法。首先，利用解析能量算子检测轴承瞬态冲击信号，计算出能量算子输出；然后，对能量序列进行傅里叶变换，得到AEO能量谱；最后在AEO能量谱中根据谱中的频率峰值和轴承的故障特征频率识别故障原因。

2.2 仿真分析

对调幅调频信号

其时域波形如图1所示，分别采用HT、TEO、AEO三种方法对该信号解调提取瞬时频率和瞬时幅值，结果如图2所示。

图1 调幅调频信号的时域波形

图2 调幅调频信号的瞬时频率估计

HT方法求得的瞬时频率和瞬时幅值在波峰和波谷与理论值相比均出现误差较大的现象；TEO方法求得的瞬时幅值与理论值吻合较好，而瞬时频率在波峰和波谷均有明显的振荡现象，这是由于信号并不能满足前述提到的TEO方法应用的要求；AEO

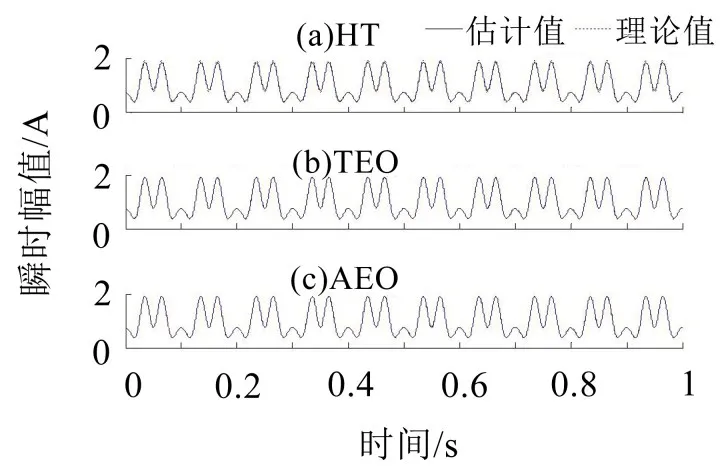
图3 调幅调频信号的瞬时幅值估计

方法所得的瞬时频率只在波谷与理论值有较小的误差，而瞬时幅值的估计值与理论值则非常吻合。

为了进一步比较三种方法得出的瞬时频率、瞬时幅值估计值与理论值的吻合程度，分别采用均方根误差和相关系数作为评价指标。三种方法得到的瞬时频率估计、瞬时幅值估计与理论值的均方误差和相关系数如表1、表2所示。可以发现：与HT、TEO方法相比，AEO方法估计的瞬时频率和瞬时幅值与理论值的相关系数更高且均方根误差更小。因此AEO方法相对HT和TEO更能有效地估计瞬时频率和瞬时幅值。

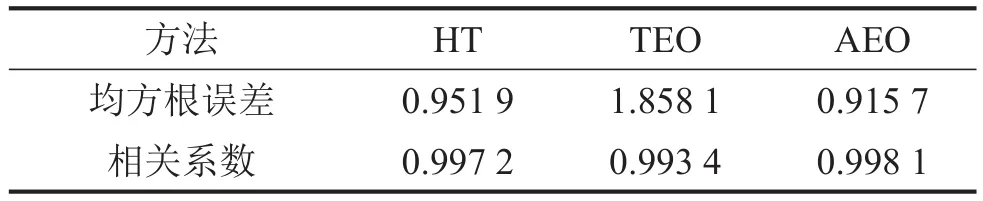
表1 三种方法得到的瞬时频率估计与理论值的误差和相关性

表2 三种方法得到的瞬时幅值估计与理论值的误差和相关性

下面考察AEO能量谱分析在滚动轴承模拟信号分析中的应用。

故障滚动轴承的冲击振动模型可以表示为

其中Am表示冲击振幅，Tp表示冲击周期，即对应的轴承故障特征频率的倒数，ωr表示系统的共振频率，ζ表示阻尼比，u(t)为单位阶跃函数，τi表示滚动体的随机滑动对冲击周期产生的偏差，一般取0.01Tp～0.02Tp，采样频率为Fs。

在仿真信号中，各参数数值见表3

表3 仿真信号参数

为了模拟实际情况，该仿真信号加上高斯噪声（SNR=-15 db）。该仿真信号的时域波形如图4所示，仿真信号的包络谱、Teager能量谱和AEO能量谱如图5所示。

图4 仿真信号的时域波形

图5 仿真信号分析

由Tp可知，故障特征频率为125 Hz。在仿真信号的时域波形中，由于噪声的影响，无法看出周期性冲击特征；包络谱中峰值频率和故障特征频率及其倍频不能对应，无法识别出故障；Teager能量谱则只能提取到故障特征频率。而AEO能量谱，可以清晰地识别出轴承的故障特征频率及其倍频，其提取出来的倍频成分可达5阶，轴承的故障特征非常明显。因此，AEO能量谱在高噪声的干扰下相对与包络谱和Teager能量谱仍能够增强故障特征，准确地提取滚动轴承的故障特征频率信息，在滚动轴承故障诊断中具有很大的潜力。

2.3 实验信号分析

为了验证本方法的优越性，在滚动轴承故障试验台上进行实验。待测的滚动轴承型号为6307E，为了模拟滚动轴承的局部损伤，实验采集正常、具有外圈故障和内圈故障三种状态的滚动轴承振动信号。根据轴承的参数，可计算出滚动轴承6307E的特征频率如表4所示。

表4 滚动轴承6307 E的故障特征频率/Hz

滚动轴承正常振动信号的时域波形和经EMD分解得到的第一个分量IMF1如图6所示，IMF1的包络谱、Teager能量谱、AEO能量谱如图7所示。从图6中可以看出，时域波形和IMF1中没有明显的冲击。图7中包络谱、Teager能量谱、AEO能量谱所提取到的频谱都没有与轴承故障特征相关的频率、倍频或者频率间隔，因此可以断定轴承正常，没有故障。

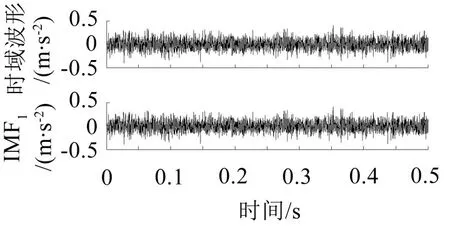
图6 正常振动信号及分量IMF1

图7 正常振动信号的IMF1分析

轴承外圈故障振动信号的时域波形和经EMD分解得到的第一个分量IMF1如图8所示，IMF1的包络谱、Teager能量谱、AEO能量谱如图9所示。由图可见，在时域波形和IMF1中虽然出现了冲击特征，但不是十分明显；从包络谱和Teager能量谱中虽然可以看出外圈故障特征频率，但是无法提取出相应的倍频。而在AEO能量谱中明显存在和轴承外圈故障特征频率35 Hz及其倍频对应的峰值频率，而且倍频阶次连续，最高达到14阶，故障特征更加明显直观。这表明AEO能量谱方法在诊断轴承外圈故障时与原有的包络和Teager能量谱方法相比更加有效。

图8 外圈故障振动信号及分量IMF1

图9 滚动轴承外圈故障振动信号的IMF1分析

轴承内圈与轴承外圈相比，故障特征更难提取。轴承内圈故障时域波形和经EMD分解得到的第一个分量IMF1如图10所示，IMF1的包络谱、Teager能量谱和AEO能量谱如图11所示。从图中可以看出，包络谱和Teager能量谱无法提取到轴承内圈故障特征频率56 Hz，而只能提取到其二倍频、四倍频、六倍频、八倍频等。而在AEO能量谱中，轴承内圈故障特征频率基频、各倍频都清晰地显示出来，且最高可达到八阶谱峰值，并且其峰值都较大，故障特征提取有效而明显。

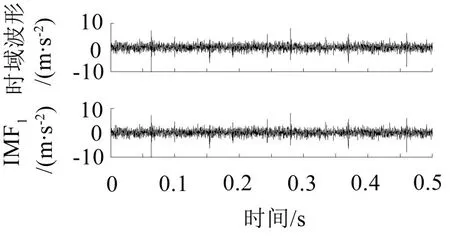
图10 滚动轴承内圈故障振动信号及分量IMF1

图11 滚动轴承内圈故障振动信号的IMF1分析

通过以上分析可知，与包络谱、Teager能量谱相比，AEO能量谱不仅能识别出故障特征较明显的外圈故障特征频率，对故障特征微弱的内圈故障征兆也能检测出来，效果明显，性能优越。

3 结语

提出了一种新的解调方法——解析能量算子解调，与Hilbert变换及传统能量算子解调相比，该方法提取的瞬时频率与瞬时幅值具有良好的局部特性且能避免振荡。针对滚动轴承故障信号的周期性冲击特性，提出了基于AEO能量谱的滚动轴承故障诊断方法，滚动轴承仿真和实验信号分析结果表明了所提出方法的有效性和优越性。

[1]FENG ZHIPENG,ZUO MING J,HAO RUJIANG,et al. Ensemble empirical mode decomposition-based teager energy spectrum for bearing fault diagnosis[J].Journal ofVibration&Acoustics,2013,135(3):1308-1308.

[2]丁康，孔正国.振动调幅调频信号的调制边频带分析及其解调方法[J].振动与冲击，2005，24(6)：9-12.

[3]罗洁思，于德介，彭富强.基于EMD的多尺度形态学解调方法及其在机械故障诊断中的应用[J].振动与冲击，2009，28(11)：84-86.

[4]曾鸣，杨宇，郑近德，等.归一化复域能量算子解调及其在转子碰摩故障诊断中的应用[J].机械工程学报，2014，50(5)：65-73.

[5]BEDROSIAN E.A product theorem for Hilbert transforms [J].Proceedings of the IEEE,1963,51(5):868-869.

[6]LIANG M,BOZCHALOOI I S.An energy operator approach to joint application of amplitude and frequencydemodulations for bearing fault detection[J].Mechanical Systems&Signal Processing,2010,24(5):1473-1494.

[7]CHENG JUNSHENG,YU DEJIE,YANG YU.The application of energy operator demodulation approach based on EMD in machinery fault diagnosis [J].Mechanical Systems and Signal Processing,21.2 (2007):668-677.

[8]鞠萍华，秦树人，赵玲.基于LMD的能量算子解调方法及其在故障特征信号提取中的应用[J].振动与冲击，2011，30(2)：1-4.

[9]MARAGOS P,KAISER J F,QUATIERI T F.Energy separation in signal modulations with application to speech analysis[J].IEEETransactionsonSignal Processing,1993,41(10):3024-3051.

[10]孟宗，季艳.基于DEMD和对称差分能量算子解调的滚动轴承故障诊断[J].中国机械工程，2015，26(12)：1658-1664.

[11]黄椒治，林慧斌，丁康.基于广义解调平滑能量分离算法的瞬时频率估计[J].振动工程学报，2014，27(2)：281-288.

[12]POTAMIANOS A,MARAGOS P.A comparison of the energy operator and the Hilbert transform approach to signal and speech demodulation[J].Signal Processing, 1994,37(1):95-120.

Application ofAnalytic Energy Operator Demodulation Method to Fault Diagnosis of Rolling Bearings

CHENG Jun-sheng,XIANG Tian-yao,YANG Xing-kai,YANG Yu
(State Key Laboratory ofAdvanced Design and Manufacture for Vehicle Body,Hunan University, Changsha 410082,China)

Aimed at the disadvantages of Hilbert transform and the conventional energy operator demodulation methods,a new demodulation method,analytic energy operator(AEO)demodulation method,is proposed.Compared to Hilbert transform and the conventional energy operator demodulation method,the AEO has higher demodulation precision. On the basis of AEO energy spectrum,a rolling bearing fault diagnosis method is put forward.This method is applied to analyze the simulated signals and actually tested signals of the rolling bearing.The comparison of the results with those of some other methods shows that the proposed method is of effectiveness and superiority.

vibration and wave;demodulation method;analytic energy operator;rolling bearing;fault diagnosis

TP911.6；TH133.3

：A DOI编码：10.3969/j.issn.1006-1355.2017.03.030

1006-1355(2017)03-0151-05

2016-12-05

国家重点研发计划资助项目（2016YFF0203400）；国家自然科学基金资助项目（51575168、51375152）；智能型新能源汽车国家2011协同创新中心、湖南省绿色汽车2011协同创新中心资助。

程军圣（1968－），男，湖南省永州市人，博士，教授，主要研究方向为机械设备状态监测与故障诊断、动态信号分析与处理。E-mail:signalp@tom.com。

向天尧，男，硕士研究生。E-mail：tianyao9276@163.com。