滤光片带宽对光电效应测量普朗克常数的影响

魏高尧，卢 忠，隋成华

(浙江工业大学 理学院，浙江 杭州 310023)

滤光片带宽对光电效应测量普朗克常数的影响

魏高尧，卢 忠，隋成华

(浙江工业大学 理学院，浙江 杭州 310023)

在光电效应测量普朗克常数实验中，由于滤光片和固体能带都具有一定的带宽，对测量的精度会产生影响.将带宽更窄的干涉滤光片取代带宽较宽的色玻璃滤光片，利用零点法、拐点法和曲率法分别测得365，405，436，546，577 nm五个波长光的反向遏止电压，并应用最小二乘法分别进行直线拟合求出普朗克常数.实验结果表明：曲率法的相对误差较其他两者小，且利用曲率法测得干涉滤光片的普朗克常数相对误差为0.04%，远小于色玻璃滤光片的相对误差(2.75%).因此利用带宽更窄的干涉滤光片可以进一步提高普朗克常数的测量精度，这有助于进一步加深理解能量量子化的概念.

普朗克常数；滤光片；带宽；精度

实验教学示范中心是目前高校培养学生创新实践能力的重要阵地，因此实验教学在高校教育中占举足轻重的地位.目前，实验教学主要分为传统实验教学[1]及虚拟实验教学.而量子理论又是近代物理学的基础之一，其中的普朗克常数h对其发展起着不可估量的作用.因而如何简单、快速而又准确地求出普朗克常数一直以来是一个研究热点.目前最常用的实验是光电效应测量普朗克常数，该实验在众多高校的近代物理实验中占据重要的地位，是各大学普遍开设的实验内容[2-7].利用光电效应测量普朗克常数实验，主要是通过测量遏止电压Ua与频率ν的关系，利用最小二乘法拟合间接求出h值.然而，光电效应测量普朗克常数实验也存在着众多影响测量精度的因素，例如暗电流的影响导致遏止电压难以精确测量、光源单色性不好及曲线拟合误差等[8].如何提高测量精度一直以来也是一个研究热点，周永军等[9]利用零点法、拐点法和曲率法确定遏止电压，普朗克常数的相对误差低至1.60%；田凯等[10]将光源的波长设计为连续可调，以此希望通过增加测试数据提高测量精度；赵加强等[11]用半导体激光器替换高压汞灯，以此提高特定波长的单色性，其测量误差降低至0.449%.在提高光源单色性方面，由于半导体激光器其波长是固定的，要获得不同波长的光，需要不同的激光器，这大大增加了实验的成本.目前通常使用的滤光片有一定的带宽，不能很好的将所需谱线以外的其它谱线滤除；另一方面，在非绝对零度情况下，固体能带也有一定的带宽，两者相互作用使测量结果产生偏差.

因此，在不改变光源的情况下，提高滤光片的单色性是增加普朗克常数测量精度较为有效的途径，而此方法的研究却鲜见报道.利用窄带宽的干涉滤光片替换宽带宽的色玻璃滤光片，有效地减小了单色光的带宽，通过测量遏止电压与频率的关系，利用最小二乘法拟合得到普朗克常数，最终将普朗克常数的测量误差降低至0.04%.

1 实验原理

当光照射在物体上时，物体以热的形式吸收光的能量只占光能的一部分，而另一部分则被物体中某些电子所吸收转换为电子的能量，这些电子获得能量后便可逸出物体表面，这种现象称为光电效应.实验表明：光电效应是实时发生的，发射电子与光照射之间的时差小于3 ns.对于每一种金属，只有入射光频率ν大于一定频率ν0才能发生光电效应现象.ν0称为“红限”，是金属的特性.发生光电效应时，出射电子气的动能可用有限深的势箱模型[12]分析：设金属的温度为T，电子发射的必要条件是电子气的动能Ek必须超过某临界值，满足

Ek≥EF+Φ

(1)

式中：EF为电子气的费米能量；功函数Φ为电子气在势箱外无穷远处的势能E∞与EF之差.

1905年爱因斯坦提出了“光量子”假设，解释了光电效应现象，即频率为ν的光子其能量为hν，即提出“红限”对应的光子能量就是金属的功函数，即Φ=hν0.在频率ν>ν0的光照射下，物体中的电子吸收了光子能量hν之后，一部分能量消耗于电子的逸出功Φ，另一部分则被电子吸收转换为电子的动能Ek,光电子动能的最大值为

Ekm=h(ν-ν0)

(2)

索末菲自由电子气模型[12]指出：电子气服从费米-狄拉克分布，在温度为T时，在费米能级以上的能态存在电子，因而光电子动能最大值只有在绝对零度是严格成立.

光电效应的实验原理[13]示意图如图1所示.在光电管的A和K之间可获得从-U到0再到+U连续变化的电压.正常光照时，加速电位差UAK转变为负值时，阴极电流会急剧减少，当加速电位差UAK减小到一定的负值时，阴极电流变为零，与此对应的电位差称为遏止电位差.这一电位差用Ua来表示.|Ua|的大小与光的强度无关，只是随着照射光的频率的增大而增大.

GD—光电管；K—光电管阴极；A—光电管阳极；G—微电流计；V—电压表；E—电源电动势；R—滑线变阻器，调节R可以得到实验所需要的加速电位差UAK图1 光电效应的实验原理示意图Fig.1 Schematic diagram of photoelectric effect experiment

Ua∝ν的关系可用爱因斯坦方程表示为

(3)

实验时用不同频率的单色光(ν1，ν2，…)照射阴极，测出相对应的遏止电位差(Ua1，Ua2，…)然后作出Ua—ν图，由此图的斜率即可以求出h.

以上是单色光照射，如果有一定带宽的光照射，由于金属能带也具有一定的带宽，两者相互作用使实验结果产生偏差.

2 仪器改进及数据分析

光电效应测量普朗克常数实验的测量装置如图2所示，主要包括汞灯光源、滤色片、光电管和测试仪等部件.汞灯通过滤光片过滤得到365，405，436，546，577 nm波长的光.实验中分别采用带宽较大的色玻璃滤光片和带宽较窄的干涉滤光片进行实验测量遏止电压并计算普朗克常数.

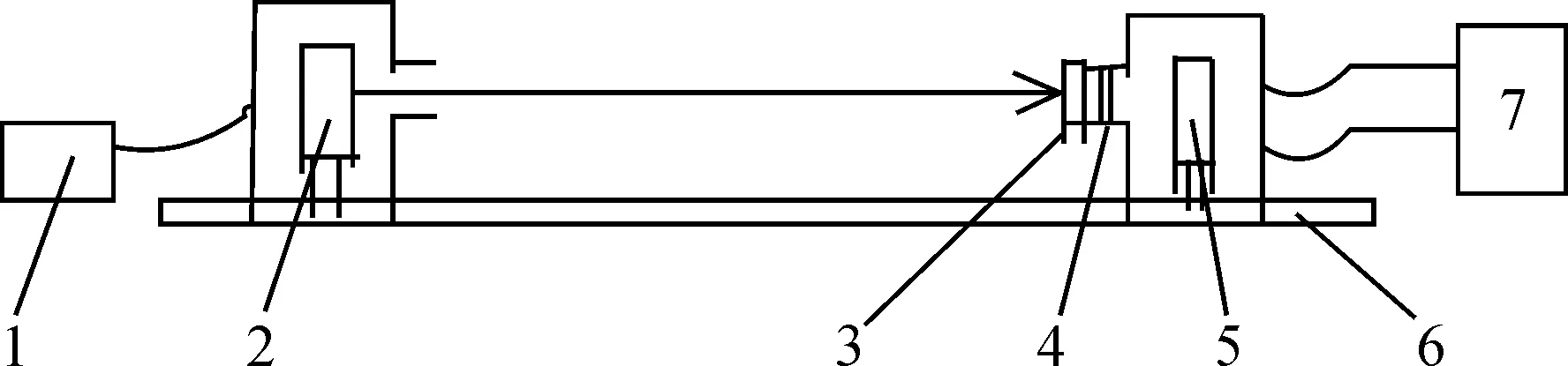
1—汞灯电源；2—汞灯；3—滤色片；4—光阑；5—光电管； 6—基座；7—测试仪图2 仪器结构示意图Fig.2 Instrument structure diagram

利用Ocean HR2000+光谱仪测出五个波长的色玻璃滤光片和干涉滤光片的透过率，如图3所示.图3(a)为汞灯光谱，其光强主要集中在365，405，436，546，577 nm五个波长处.从图3(b～f)可以看出：干涉滤光片在五个波长处的透过率高于80%，其带宽分别为64，26，28，28，25 nm；而色玻璃滤光片在365，405，436，546 nm四个波长处的透过率低于50%，且四个波长处的带宽分别为39，35，57，41 nm.因此，无论是从透过率还是从带宽方面看，干涉滤光片都优于色玻璃滤光片.

图3 汞灯光谱及两种滤光片对五个波长的透过率谱Fig.3 Mercury lamp spectrum and five wavelength transmittance spectrum of two filters

遏止电压的确定方法[9,14]有：零点法、拐点法和曲率法.用零点法确定遏止电压，由于暗电流及本底电流的存在，使得测定的电压U并不等于遏止电压Ua，存在实验误差；用拐点法确定遏止电压，由于光电流被遏止的点所对应的电压选取随意性较大，因此也存在误差；用曲率法确定遏止电压，由于I—U曲线中直线与曲线分段点的选用存在不确定因素，因此也会产生误差，曲率法还存在数据处理繁琐的问题.实验表明[14]曲率法中利用Boltzmann函数对I—U曲线进行不分段拟合，并利用拟合函数计算光电流为零的电压值，即遏止电压来测定普朗克常数，不仅处理简单而且误差也较小.笔者利用零点法、拐点法和Boltzmann函数拟合法来确定遏止电压.

分别利用色玻璃滤光片和干涉滤光片进行实验，分别测得五个波长下阴极电流与加速电位差的I—U曲线关系，零点法及拐点法确定遏止电压可以从I—U曲线中直接得出，如表1所示.

表1 两种滤光片测得的遏止电压

曲率法是利用Boltzmann函数拟合，其拟合函数为

I=A2+(A1-A2)/[1+exp((U-x0)/dx)]

(4)

式中：I为阴极电流；U为加速电位差；A1，A2，x0，dx为拟合系数.以436 nm波长为例，色玻璃和干涉玻璃测得的I—U曲线、拟合曲线及拟合系数值如图4(a，b)所示.根据式(4)和拟合系数可以计算出色玻璃滤光片和干涉滤光片I等于零时的U分别为-1.211，-1.189 V，即为遏止电压.利用相同的方法，测出色玻璃滤光片和干涉滤光片其余四个波长的遏止电压，如表1所示.

图4 436 nm色玻璃滤光片和干涉滤光片的I—U关系及拟合曲线Fig.4 I-U curves and fitting curves of 436 nm stained glass and interference filters

根据表1所列数据，分别画出三种方法下两种滤光片的遏止电压与频率的关系曲线，如图5所示.利用最小二乘法对其进行线性拟合，得到零点法、拐点法和曲率法的色玻璃滤光片的斜率分别为-4.014×10-15，-4.299×10-15，-4.024×10-15；干涉滤光片的斜率分别为-4.131×10-15，-4.057×10-15，-4.138×10-15.拟合的R2都大于0.99，拟合度较高.根据式(3)可计算出普朗克常数，根据普朗克常数的公认值为6.626 068 96×10-34J·s，可计算出相对误差，如表2所示.从表2可以看出：曲率法测得的相对误差较其他两者要小，其计算出的相对误差分别为2.75%，0.04%，三种方法下干涉滤光片的相对误差都比色玻璃滤光片的要小.因而采用带宽更窄的干涉滤光片可以有效提高光电效应测量普朗克常数实验的测量精度.

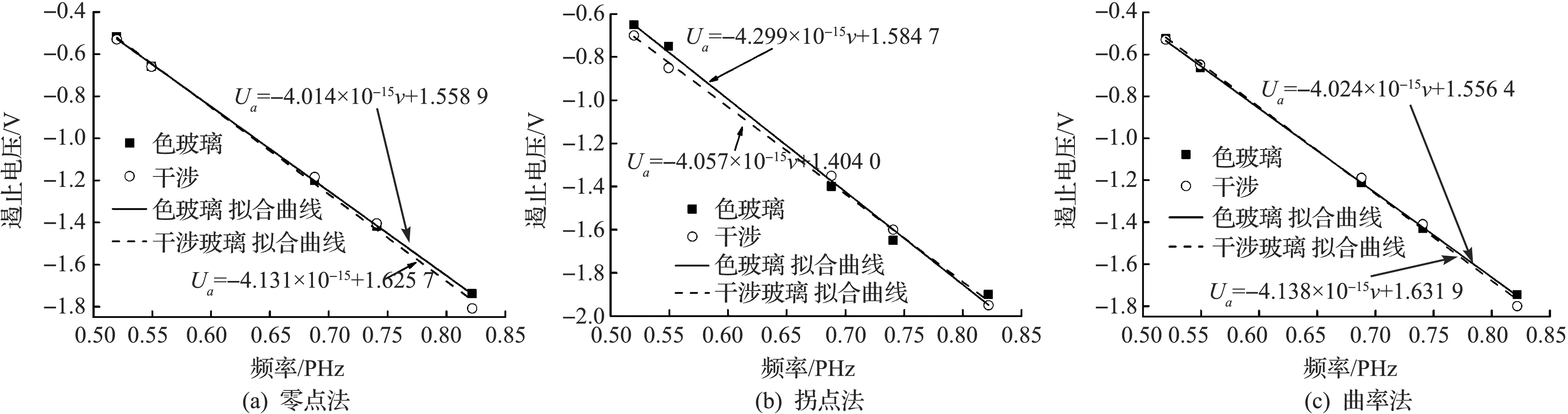
图5 三种方法下两种滤光片遏止电压与频率的关系及其拟合曲线Fig.5 Voltage-frequency of two filters and fitted curves utilizing three methods

方法名称斜率h/(J·s)相对误差/%零点法色玻璃滤光片-4．014×10-156．43043×10-342．95干涉滤光片-4．131×10-156．61786×10-340．12拐点法色玻璃滤光片-4．299×10-156．88727×10-343．94干涉滤光片-4．057×10-156．49943×10-341．91曲率法色玻璃滤光片-4．024×10-156．44528×10-342．72干涉滤光片-4．138×10-156．62892×10-340．04

3 结 论

在不增加实验复杂度的情况下，利用带宽更窄的干涉滤光片替代色玻璃滤光片，可以有效的提高普朗克常数测量的精度，通过零点法、拐点法和曲率法分别测量遏止电压并利用最小二乘法拟合遏止电压与频率的关系曲线，最终相对误差可以降低至0.04%.通过两种不同带宽的滤光片测量普朗克常数，可以进一步加深对能量量子化概念的理解.

[1] 许周速，周莹，严金华，等.光纤光栅温度传感教学实验装置设计与实现[J].浙江工业大学学报，2016,44(1)：108-110.

[2] 陈早生，任才贵.大学物理实验[M].上海：华东理工大学出版社，2003：231-235.

[3] 滕道祥.大学物理实验[M].北京：北京理工大学出版社，2006：156-162.

[4] 李朝荣，徐平，唐芳，等.基础物理实验[M].北京：北京航空航天大学出版社，2010：242-247.

[5] 韩忠，刘安平.近现代物理实验[M].北京：机械工业出版社，2012：62-65.

[6] 隋成华.大学物理实验[M].上海：上海科学普及出版社，2012：78-82.

[7] 李治中.工科大学物理实验[M].北京：高等教育出版社，2015：155-165.

[8] 黄曙江.普朗克常数测量中的不确定的分析[J].计量与测试技术，2007，34(11)：1-2.

[9] 周永军，朴林鹤，吕佳.在光电效应测定普朗克常数实验中测量方法的讨论[J].沈阳航空航天大学学报，2011，28(2)：85-87.

[10] 田凯，王照平，蔡晓艳.一种测定普朗克常数的综合实验装置[J].实验室研究与探索，2014，33(12)：58-61.

[11] 赵加强，胡绪瑞.用半导体激光器作为光源改进普朗克常数测定仪[J].激光杂志，2015,36(11)：83-85.

[12] 陆栋，蒋平，徐至中.固体物理学[M].上海：上海科学技术出版社，2003.

[13] 侯春，隋成华，徐来定，等.光电效应实验中的误差分析及消除方法[J].光学仪器，2002,24(4/5)：14-17.

[14] 闻春敖，郑晓东.光电效应法测量普朗克常数的数据处理及误差分析[J].光学技术，2009,35:191-193.

(责任编辑：陈石平)

Effects of filter bandwidth on measurement of Plank constant using photoelectric effect

WEI Gaoyao, LU Zhong, SUI Chenghua

(College of Science, Zhejiang University of Technology, Hangzhou 310023, China)

In the experiment of Plank constant measurement with photoelectric effect method, the accuracy of measurement will be affected by the bandwidth of filter and solid energy band. The reverse cut-off voltages of 365, 405, 436, 546, 577 nm wavelengths are measured by using null point, turning point and curvature methods with the interference filter with narrow bandwidth in place of stained glass filter with broad bandwidth . Then the Plank constant is determined by using line fitting with least square method. The experimental results show that the relative error using curvature method is less than the other two. The relative error of Plank constant measured by curvature method using interference filter is 0.04%. It is far less than that using stained glass filter (2.75%). The interference filter with narrow bandwidth can improve the measuring accuracy of Plank constant. It can further comprehend the concept of energy quantization.

Plank constant; filter; bandwidth; accuracy

2016-10-08

国家自然科学青年基金资助项目(11404286)；浙江省高等教育教学改革项目(jg2015029)；2015高等学校教学研究项目(DWJZW201523hd)

魏高尧(1962—)，男，浙江诸暨人，高级实验师，主要从事物理实验、光电子学和仪器开发等教学与科研工作，E-mail：wgy@zjut.edu.cn.

O431.2

A

1006-4303(2017)03-0342-05