浅析求解向量题目常用的妙招

2017-06-27王子睿

神州·下旬刊 2017年1期

王子睿

摘要：向量题目是试卷中必定出现的题目，直接解答向量题目，往往找不到入手点，可以从几何与代数两个角度，将其进行转化，就可以轻松解答。从代数角度来讲，可以将向量问题实数化，从而运用数的性质加以处理；从几何角度来讲，向量问题可以运用数形结合思想加以处理。文中，介绍了求解向量题目常用的妙招，以求能够更好地解决向量问题。

关键词：向量题目；高中数学；妙招

向量，就是指既有大小又有方向的量，它的本质解释了向量具有“数”和“形”的双重身份。向量题目的难度并不是很大，而是转化起来存在困难，导致出现问题。在解决向量题目是，可以根据具体问题，从代数与几何两个角度着手转化，切在实践中反思，形成解决向量题目的妙招。

1.灵活“建系”，巧妙解答向量题目

遇到平面图形的向量问题时，可以根据需求，灵活建立平面直角坐标系，然后在通过向量坐标运算巧妙地解决问题。这正是体现向量“代数化”手段的重要性，更是解决向量问题的妙招。

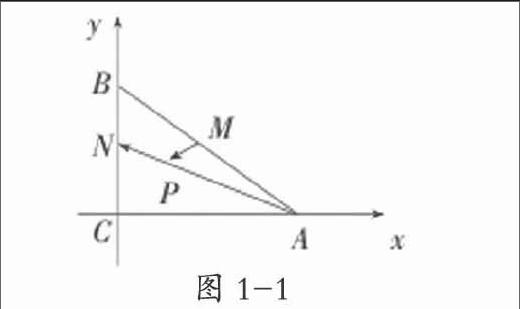
例1 在等腰直角三角形ABC中，AC=BC=1，点M，N分别是AB，BC的中点。若点P是ΔABC内部任意一点，那么AN·MP的取值范围是。

【分析】该题目解决之前，首先要根据题意构建一个平面坐标系xcy，且将等腰直角三角形ABC置放于平面坐标系xcy中（如图1-1）。根据图1-1可以发现，点A（1，0）， N（0，1/2），M（1/2，1/2）。设点P的坐标为（x，y），则可以得出么AN=（-1，1/2）；MP=（x-1，y-1/2）。

解（略）

【评注】该题目是一道综合性的题目，通过抽象思维很难找到出路，而通过建立一个平面直角坐标系，就能够找到解题思路，同时还能够找到切入点。“平移”是运用线性规划解题过程中常常用到的技巧，在此题目中，就是运用“平移”技巧，建立不等式，最终解决问题。

2.构造“基底”，巧妙解答向量题目

平面向量问题往往较为抽象，看到题目只觉地眼花缭乱，根本不能够抓住题目的切入点，更不能正确、省时地解决问题。如若遇到平面向量的相关问题，能够根据具体情况，选择一组恰当地基底，就能够将繁琐的问题化简单的问题。选择基底不能够随便选择，而是要依据平面向量的基本定理和向量相关的知识点。选择恰当基底e1、e2，就可以将原来的向量问题转化成为e1、e2的代数运算的问题。

例2 （2015年福建高考题）已知AB⊥AC， |AB|=1/t， |AC|=t，若点P是ΔABC所在平面內的一点，且AP=，

则PB·PC的最大值为

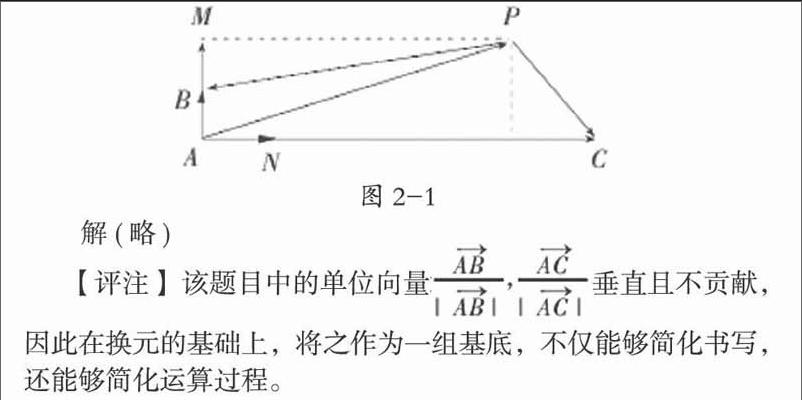
【分析】该题目中向量AP的表述非常繁琐，这无疑在解题的路上置放了一个拦路虎，且教容易出现错误。此时，根据题意和平面向量的基本定理及相关向量知识，选定一组基底e1、e2，就可以将繁琐的向量问题，转化成为基底e1、e2的代数运算。构建平面坐标系，根据题意画图如图2-1

解（略）

【评注】该题目中的单位向量垂直且不贡献，

因此在换元的基础上，将之作为一组基底，不仅能够简化书写，还能够简化运算过程。

3.借助“图形”，巧妙解答向量题目

向量具有“数”和“形”的双重身份，因此在遇到向量问题时，不仅要能够灵活地运用平面向量的加法原则和减法原则，还能够明确其几何意义，且能够结合题意恰当的运用。因为对于抽象的问题，往往可以通过图形进行简化，且有助于找到正确的解题思路，从而顺利地完成题目。

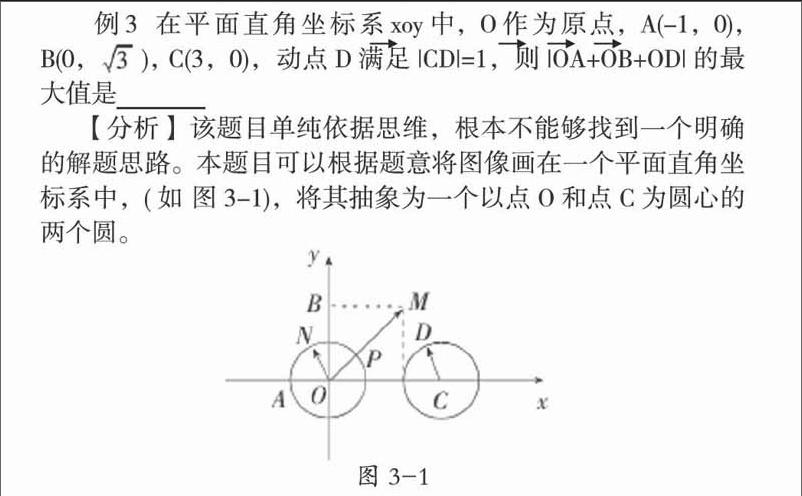
例3 在平面直角坐标系xoy中，O作为原点，A（-1，0）， B（0，）， C（3，0），动点D满足|CD|=1，则|OA+OB+OD|的最大值是

【分析】该题目单纯依据思维，根本不能够找到一个明确的解题思路。本题目可以根据题意将图像画在一个平面直角坐标系中，（如图3-1），将其抽象为一个以点O和点C为圆心的两个圆。

解（略）

【评析】将题意形成具体的某个图像并不是解题的关键，该题目根据绘制图形，处理的关键在于三点：一是，将向量OD分别成为OC与CD两个向量；二是做向量ON，且是向量ON=CD；三是，灵活运用向量不等式|a+b|≤|a|+|b|取等号的充分必要条件。