基于总体最小二乘切片的孔洞修补方法研究

2017-06-26孟庆年郑德华张崇军

地理空间信息 2017年6期

关键词：剖分孔洞总体

孟庆年，郑德华，张崇军

（1.河海大学地球科学与工程学院，江苏南京 210098 ）

基于总体最小二乘切片的孔洞修补方法研究

孟庆年1，郑德华1，张崇军1

（1.河海大学地球科学与工程学院，江苏南京 210098 ）

对点云孔洞的修补进行研究是点云数据处理的重要部分。对常用的孔洞修补方法进行了介绍，并详细介绍了基于切片的孔洞修补方法。通过引入总体最小二乘方法对基于切片的孔洞修补方法进行改进，使修补的精度得到提高。通过对比常用的修补方法在复杂孔洞修补中的应用，基于总体最小二乘的切片方法的修补效果更优。

孔洞修补；复杂孔洞；切片方法；总体最小二乘方法

近些年来，随着三维激光扫描技术及其相关技术的快速发展，三维激光扫描技术已广泛应用于各个领域[1]。但在使用三维激光扫描仪时，往往会因为扫描对象的自身部位遮挡、外物遮挡或者点云数据预处理等原因造成数据缺失，从而在扫描点云上形成孔洞[2]。而这些数据缺失的存在不仅会对建模的质量造成严重影响[3]，而且对于模型的有限元分析以及模型快速制造等后续操作也有很大的影响[4]。因此，对于点云的孔洞修补方法进行研究是十分必要的。目前，常用的是基于网格的孔洞修补方法，对于一般的孔洞修复效果良好，但是对于孔洞区域含有多种曲面的情况，往往修复效果不佳或失效。而基于切片的孔洞修补方法不仅能够修复常见的简单孔洞，还能够修复各种复杂的孔洞。目前对基于切片的修补方法研究较少，而且都是基于简单的最小二乘方法。本文通过引入总体最小二乘方法对系数矩阵和观测向量进行修正，从而提高切片方法拟合修补的精度[5]。

1 孔洞边界的检测提取

根据孔洞的形状，大致可将孔洞分为简单孔洞、复杂孔洞以及环形孔洞。本文以简单孔洞为例，对孔洞的边界进行提取。孔洞的边界检测提取大致包括K邻点数据的拓扑搜索、点云数据的法矢计算、边界点的确定以及内边界提取[6]。

1）K邻点数据的拓扑搜索。常用的K邻点搜索方法有空间格网方法、K-d tree方法以及八叉树等方法，本文使用空间栅格方法对点云数据建立拓扑关系，通过计算以及调整求得空间格网的最终边长，通过划分建立网格之间的拓扑关系。

2）点云数据的法矢计算。根据已经确定好的数据点的K邻域构成一个平面，使用最小二乘方法进行拟合，这个平面的法矢即为数据点的法矢，对法矢的方向进行检测，确保指向一致。

3）边界点的确定以及内边界提取。将数据点的K个邻点按计算出的法矢投影到数据点的平面上，计算数据点与邻点连线之间的夹角，根据夹角的最大值判断是否为边界点。将边界点进行连接，通过一定的判别准则，将内边界提取出来。

2 基于三角剖分的孔洞修补方法研究

孔洞的修补方法大致可分为3类：基于体数据的孔洞修补方法、基于网格的孔洞修补方法以及基于切片的孔洞修补方法。目前最为常用的是基于网格的孔洞修补方法，本文以三角剖分方法为例，详细介绍修补的过程。

以得到的孔洞边界为基础，对孔洞区域进行修补，三角剖分方法的主要思想是局部扩张并填充，假设两边界边的夹角为α，填充过程如下[7]：

1）当边界边夹角α≤0.5π时，将边界端点进行连接形成一条新的边界边，生成一个新的三角面片。

2）当0.5π＜α≤ π时，平分边界边夹角α增加一个端点，记录新生成的端点，形成两条新的边界边，并生成两个三角面片。

3）当π＜α≤1.5π时，三等分边界边夹角α新增两个端点，记录新生成的端点，形成三条新的边界边，并生成3个三角面片。

4）当1.5π＜α≤2π时，四等分边界边夹角α新增3个端点，记录新生成的端点，形成4条新的边界边，生成4个三角面片。

通过对边界边夹角的遍历，使空洞区域逐步填充，对新生成的点进行保存，从而达到孔洞填充的目的。孔洞填充完毕后，还需对最后生成的三角片进行合法性检测即可得到修补的点云数据。

3 基于切片的点云孔洞修补方法研究

基于切片的修补方法不仅能够修补普通的孔洞，而且还能够修补各种复杂的孔洞，尤其是孔洞区域含有多种曲面的复杂孔洞。基于切片的修补方法主要包含两个步骤：切片宽度的确定和切片的投影拟合。

3.1 切片宽度的确定

切片宽度的确定常用的方法是密度法，本文介绍两种密度法。

1）基于空间格网划分的密度法。

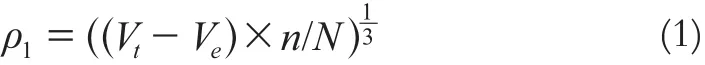
式中，Vt为所有的空间网格的个数；Ve为所有空的空间网格的个数；n为邻近点的个数；N为所有的数据点个数。

式中，δ为切片宽度；ρ1为栅格法求得的点云密度；k1一般取值4～8。

2）基于邻近点搜索的密度法[8]。

式中，n为点的个数；m为搜索的最邻近点个数；D为数据点到m个邻近点距离之和。

式中，δ为切片宽度；ρ2为最邻近点法求得的点云密度；k2一般取值1～4。

3.2 基于最小二乘的切片投影拟合方法

根据计算所得的切片宽度，首先需要对切片进行划分，然后对切片进行投影拟合。

1）切片划分。以单向切片为例进行研究，首先确定切片方向。以X方向为主方向对点云进行切片处理，则可以得到间距一定的多条切片。

2）切片投影拟合。对获得的点云切片逐条处理，首先对切片进行投影，可以得到二维的散乱点。对二维的散乱点进行拟合，目前常用的方法是最小二乘拟合方法。设曲线的函数为：

设点云的个数为n，φ0(x)=1，φ1(x)=x，φ2(x)=x2，令每个点的权重ωi相同，且都为1。由式（6）可以求解出a、b、c，从而得到拟合函数。

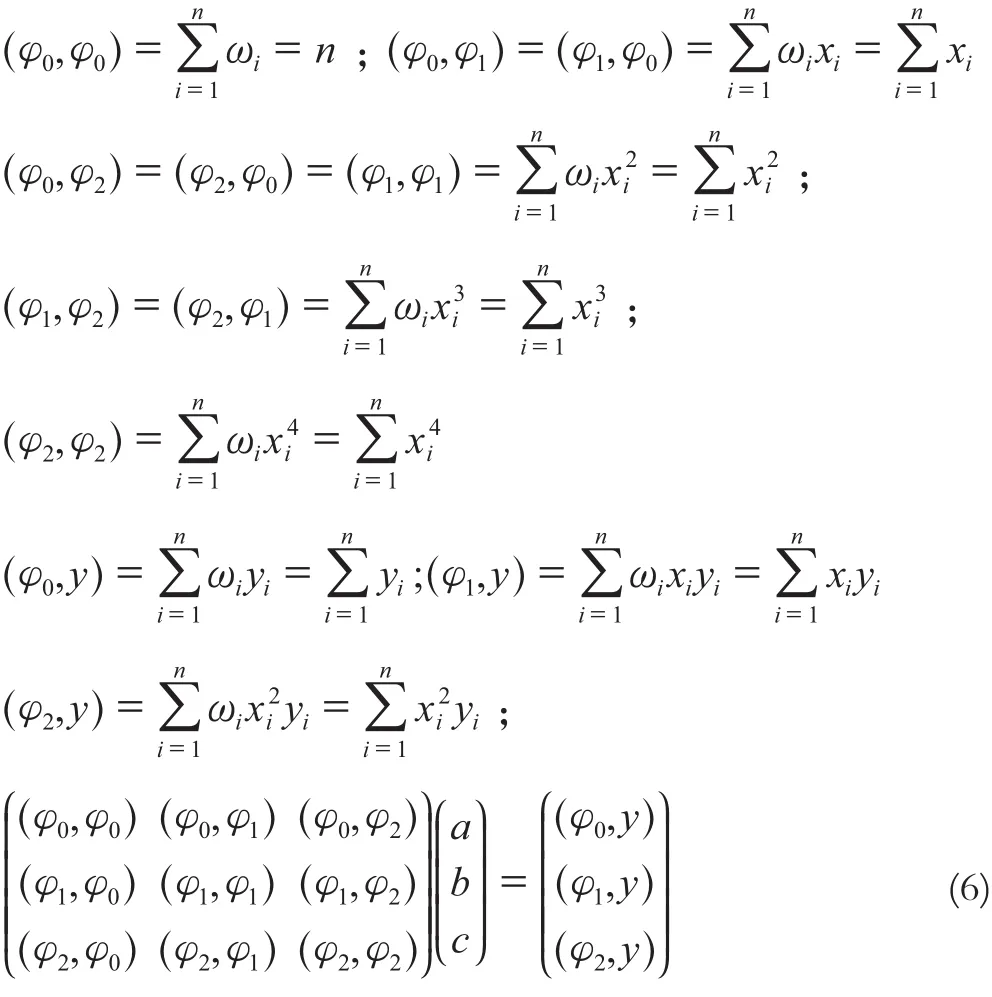
3.3 基于总体最小二乘的切片投影拟合方法

在数据采集过程中，假设每个点的采集误差相等，并且每个点的三个维度的坐标也是等误差的，数据点是必然含有误差的。在进行数据处理的过程中，对切片进行拟合时，因为其系数矩阵和观测向量是以原始数据为依据的，所以必然含有误差，如果直接使用将会对拟合修补结果造成影响。

总体最小二乘的基本思想是在观测方程中，不仅观测向量中存在误差，同时系数矩阵中也含有误差。所以，由式（6）中的观测方程[9]：

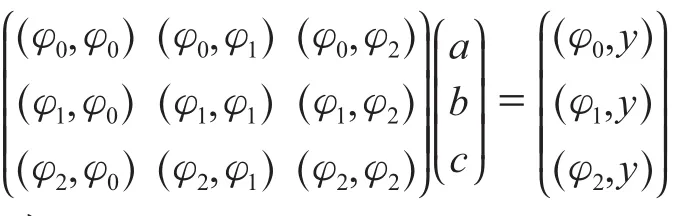
可以表示为：

总体最小二乘表达式为：

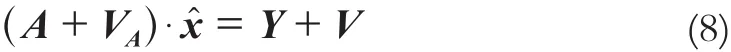
本文使用SVD奇异值分解方法对总体最小二乘进行求解。

1）对构造的增广矩阵[A Y]进行分解得：

2）判断V22是否为奇异矩阵，若V22非奇异，则：

3）总体最小二乘方法计算得到的残差矩阵为：

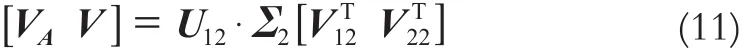
对于切片投影的拟合图如图1，通过对系数矩阵误差的考虑，基于总体最小二乘的拟合方法的效果明显优于最小二乘方法的拟合效果。

图1 切片投影拟合图

4 实验案例

使用Trimble GX三维激光扫描仪对某石质雕塑进行扫描，得到三维扫描数据在表面起伏复杂部位人为制作孔洞（如图2），方便后续的实验对比。

图2 三维激光扫描点云及孔洞附近点云示意图

首先，对孔洞的内边界进行提取得到内边界（如图3）。使用三角剖分的方法进行孔洞修补（如图4），从修补的结果可以看出，修补的孔洞部分的点位分布不均匀且与周边数据的连接不光滑。使用切片方法进行孔洞修补（如图5），从修补的结果可以看出，修补的孔洞部分的点位分布均匀且与周边数据的连接较为光滑。

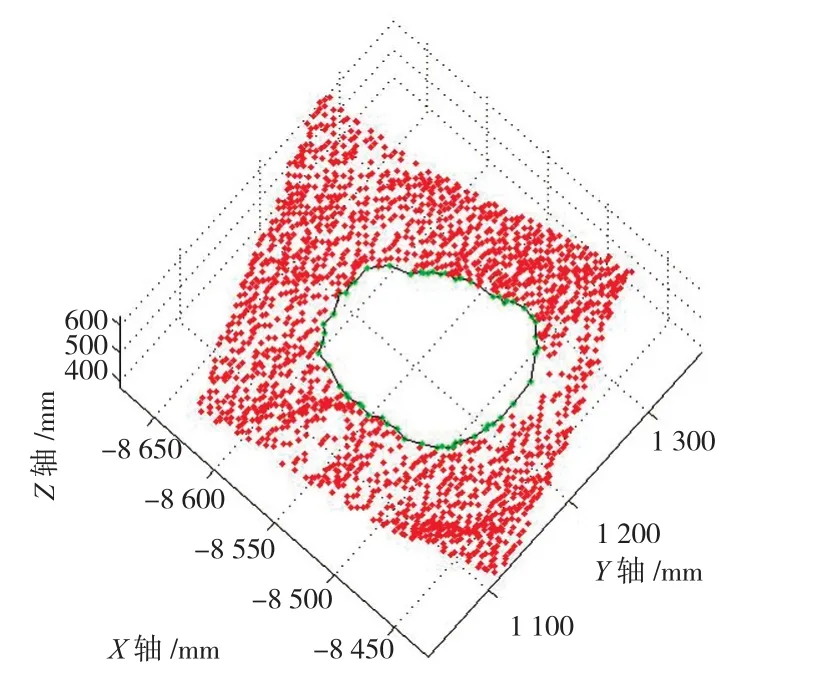
图3 孔洞内边界示意图

图4 三角剖分方法修补示意图

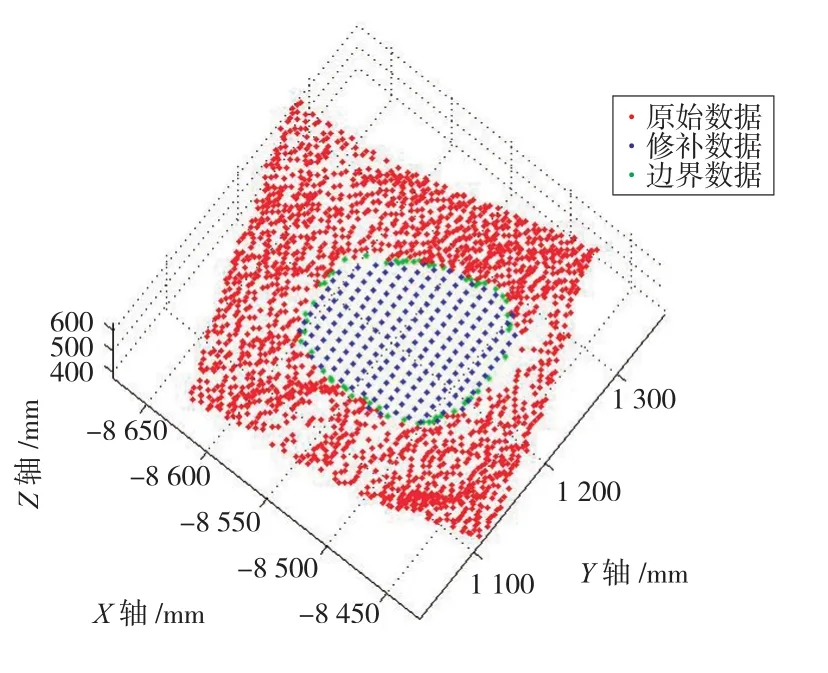
图5 切片方法修补示意图

对孔洞的点云数据分别使用基于三角剖分的孔洞修补方法、基于神经网络的孔洞修补方法、基于最小二乘切片的孔洞修补方法以及基于总体最小二乘切片的孔洞修补方法对点云孔洞数据进行修补，修补结果如表1。从修补的效果上看，基于切片的修补方法的效果明显优于三角剖分方法和神经网络方法，而基于总体最小二乘的切片方法考虑到系数矩阵的误差，使得拟合的效果更优。