利用对数函数获取正射立体影像对的方法

武 坚，李燕军，滕 飞，张 民，吕郁青

（1. 61243部队，新疆 乌鲁木齐 830006）

利用对数函数获取正射立体影像对的方法

武 坚1，李燕军1，滕 飞1，张 民1，吕郁青1

（1. 61243部队，新疆 乌鲁木齐 830006）

数字正射影像没有三维立体信息，对地物陡坎高度或沟渠深度不能量测，探讨引入对数函数生成投影光线，通过数字微分纠正的方法，制作立体辅助影像，并与原正射影像共同构成立体正射影像对，构建与实地相似的几何模型进行立体量测，获取地物高度信息，解决城市建设等单位的实际需求。最后给出了实验结果，并对其量测的高差成果也进行了检测。

对数函数；微分纠正；立体正射影像对；可量测性

通过人工引入视差在右正射影像上制作立体辅助影像，并与左正射影像组成立体正射影像对[1]，可以进行立体观测，得到与实地相似的真三维立体环境，对正射立体影像对进行三维量测，脱离立体量测必须依靠原始立体影像构建立体模型的传统方法[2]，可解决地物细节，如陡坎高度或沟渠深度的量测问题[3]。本文探讨将对数作为投影视差引入函数，采用微分纠正的方法，制作具有左右视差的立体辅助影像，建立立体正射影像对，量测几何模型，并给出实验成果及精度检验结论。

1 对数投影法引入人工视差的数学基础

平行光线投影引入的视差是高差的线性函数，这与原始立体像对的高差有不相符之处[4]。为了提高利用所制作立体辅助影像构建立体模型的量测精度，可采用对数函数引入投影光线，作为立体模型左右视差的基础。对数投影法引入人工视差的原理如图1所示。

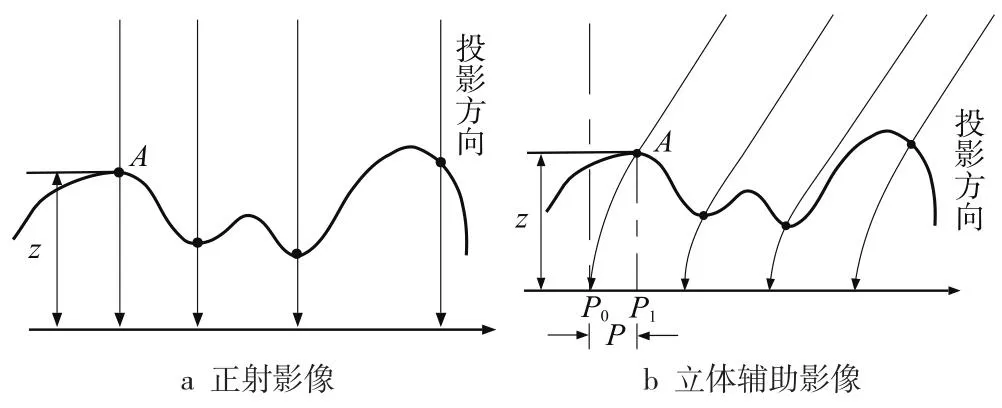
图1 对数法投影原理

对数投影法引入视差的函数为：

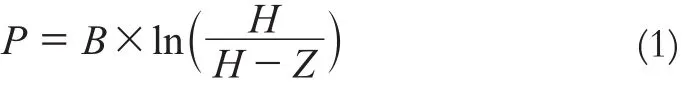
式中，P为高程Z对应的视差；B为摄影基线；H为航高；Z地面点高程。

对数曲线投影光线与DEM表面的交点为B点，如图2。

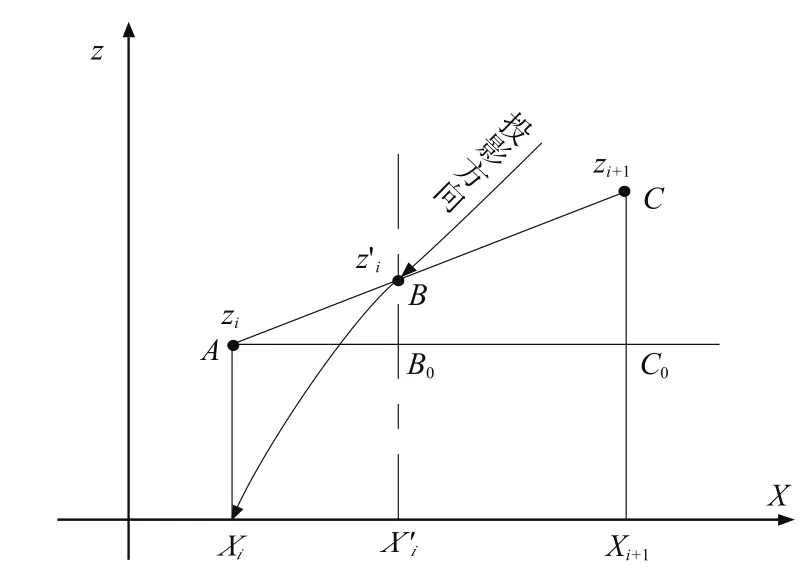
图2 对数投影交点计算

对数曲线投影光线与DEM表面格网点线性内插的交点B坐标（Xi，Yi，Zi），可通过（2）式进行计算：

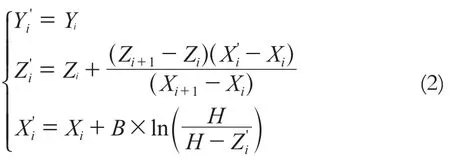
对数函数投影中，立体正射影像对中任意一点B的高程，可以由式（1）求出：

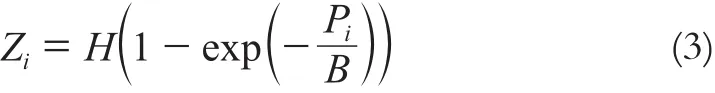
2 微分纠正法生成立体辅助影像的过程

在数字微分纠正中[5]，采用正解法进行正射影像纠正的过程时[6]，将DEM网格点垂直投影到正射影像上得到大地坐标，然后将对数投影函数所生成的光线投影到DEM上，得到交点的新大地坐标，利用共线方程解算对应的像点坐标[7]，并将该像点灰度值赋给所求解算影像的网格点。网格内部影像像点通过双线性内插得到灰度值[8]，从而得到立体辅助影像。

采用微分纠正法制作立体辅助影像的求解步骤为：

1）将XY平面上与DEM的格网间隔大小相同的方格网按照投影方向平行于XZ平面的人工对数投影视差函数（图2）把网格的4个角点分别投影到DEM上，进而得到投影光线与DEM的交点（Xi′，Yi′，Zi′）坐标。

2）利用共线方程将投影后与DEM相交的4个格网点变换到原始影像，得到对应的像点坐标。

3）利用内定向参数，由像点坐标计算相应的扫描坐标。

4）对每一格网块内的4个格网点按照共线方程求出其像点坐标，然后根据内定向参数将其转化为扫描坐标，对于每一格网块内部按照双线性变换法逐点计算其扫描坐标。由于所求像点坐标不一定落在像元中心位置，再采用双线性插值法内插出每个像元的灰度值[5]。

5）灰度赋值。将内插后的每个灰度值逐像素赋给纠正后的像元。

3 立体辅助影像生成的实例及分析

根据前述理论对卫星影像采用微分纠正法制作立体辅助影像（如图3）。采用IKONOS卫星影像，正射影像分辨率为1 m，对应DEM格网间距为20 m。正射影像对的三维量测环境采用正射影像和立体辅助影像构建，立体辅助影像采用对数投影函数引入人工视差生成投影光线。

图3 生成的立体辅助影像

将所制作的立体辅助影像，与原正射影像构建立体正射影像对进行高度（如楼高、桥高等）量测[8]。结果与数字摄影测量工作站中采用航空立体像对量测的对应地物高度数据进行精度对比，如表1。

表1 地物高度量测结果

由实验结果分析可知：

1）由于原始DOM上本身就存在地物影像的相关信息，通过构建的立体正射影像对所量测的地物高度能够在几何模型上直接获取。

2）微分纠正法制作立体辅助影像时，需要已知左右原始影像、每张像片的内、外方位元素及对应区域的DEM数据，通过严密的共线条件方程和对数视差投影函数进行影像数据求解。

3）在DEM数据精度可靠的情况下，对数投影函数所生成的立体辅助影像对可以确保地物量测精度，这主要是由于每个像点的人工视差的引入都是通过严格的对数函数关系计算而得，立体量测实质上是公式的反解求值，即根据量左右视差计算该量点的高程值。

4 结 语

地质矿产部门对陡坎高度或小沟深度、城市建设部门对建筑物的高度、林业部门对各类树木的高度等有实际需求，这些信息存在遥感影像所获取的原始的立体像对中，也存在于所制作的正射影像图中。对于原始的立体影像对，好多只是作为过程产品，而没有作为最终成果保存，导致不能重复利用。本方法可直接利用作为测绘产品之一的正射影像来生成立体像对，并进行量测，达到对不同地物高度或深度量测的需求。

[1] 周杨．基于正摄影像的地形双模立体景观构建方法[J]．测绘科学技术学报,2012,29(2)：162-167

[2] 耿则勋,张保明,范大昭．数字摄影测量学[M]．测绘出版社,2010

[3] 李德仁,王密．一种基于航空影像的高精度可量测无缝正射影像立体模型生成方法及应用[J]．铁道勘察,2004,30(2)：89-91

[4] 滕飞．遥感影像双模三维地理环境构建技术的研究[D]．信息工程大学,2013

[5] 郭海涛．基于卫星遥感影像的单片测图与修测[D]．信息工程大学,2002

[6] 智长贵,郎奎建．帽儿山林场航空像片数字立体正射影像图制作及应用[J]．东北林业大学学报,2005,30(2)：134-138

[7] 刘风德．基于左右正射影像的三维量测方法的研究[J]．测绘科学,2004,29(3)：74-78

[8] 王争鸣,王玮,任晓春．一种基于立体正射影像对的大场景立体模型生成及量测方法 [Z]．2010

P237

B文章编号：1672-4623（2017）06-0070-02

10.3969/j.issn.1672-4623.2017.06.021

武坚，硕士，高级工程师，主要从事摄影测量研究。

2015-04-24。