棱镜式激光陀螺多温度点的零偏补偿方法
2017-06-26何晓莉陶渊博
何晓莉,陶渊博,2
(1.西安北方捷瑞光电科技有限公司,陕西 西安 710111;2.西北工业大学 自动化学院,陕西 西安 710129)
棱镜式激光陀螺多温度点的零偏补偿方法
何晓莉1,陶渊博1,2
(1.西安北方捷瑞光电科技有限公司,陕西 西安 710111;2.西北工业大学 自动化学院,陕西 西安 710129)
棱镜式激光陀螺的光路与反射镜式激光陀螺的光路不同,有较长的光路在棱镜中通过,其零偏受温度影响较大。文中分析了棱镜式激光陀螺的零偏温度特性,研究了零偏与温度、温度变化率和温度梯度的相关关系。建立了复杂温变环境下多温度点的二阶动态温度模型,优化出对陀螺零偏贡献最大的两个温度检测点,并对随机温变数据进行补偿。结果表明,多温度点的二阶动态温度模型能很好地补偿复杂温变引入的零偏变化,使零偏稳定性提高60%以上。
棱镜;激光陀螺;光路;温度检测点;补偿
在捷联惯导系统中,激光陀螺是其核心敏感元件之一,其性能的好坏对惯导系统的精度起着决定性的作用。在复杂的温变环境下,反射镜式激光陀螺的性能受到较大的影响,而棱镜式激光陀螺相比反射镜式而言,有很大一部分光路在全反射棱镜中通过,温度对其影响更加剧烈,因此温度已成为制约棱镜式激光陀螺精度的主要因素之一[1]。
传统的温度补偿方法均是针对于单温度点,在缓变的温度下,补偿是有效的;而在复杂的温变环境下,就需要考虑温度梯度及温度变化率的影响。一些学者已经研究了复杂温变环境下零偏的补偿,并取得了一定的成绩[2-7]。本文结合棱镜式激光陀螺的特点,从陀螺零偏温度特性着手,找出对零偏影响较大的温度检测点,并在某型棱镜式激光陀螺上进行了试验。
1 棱镜式激光陀螺零偏温度特性
温度对棱镜式激光陀螺的影响是一个综合过程,既会影响环形激光器工作气体的物理特性,也会影响激光陀螺的结构参数,进而引起激光陀螺的零偏误差。
1.1 温度对工作气体物理特性的影响
温度变化会引起环形腔内氦、氖气体压强产生变化。同时环形激光器的输出功率与氦氖气体的比例(简称气比)及压强密切相连。不同气压、气比下的激光输出功率如图1所示。
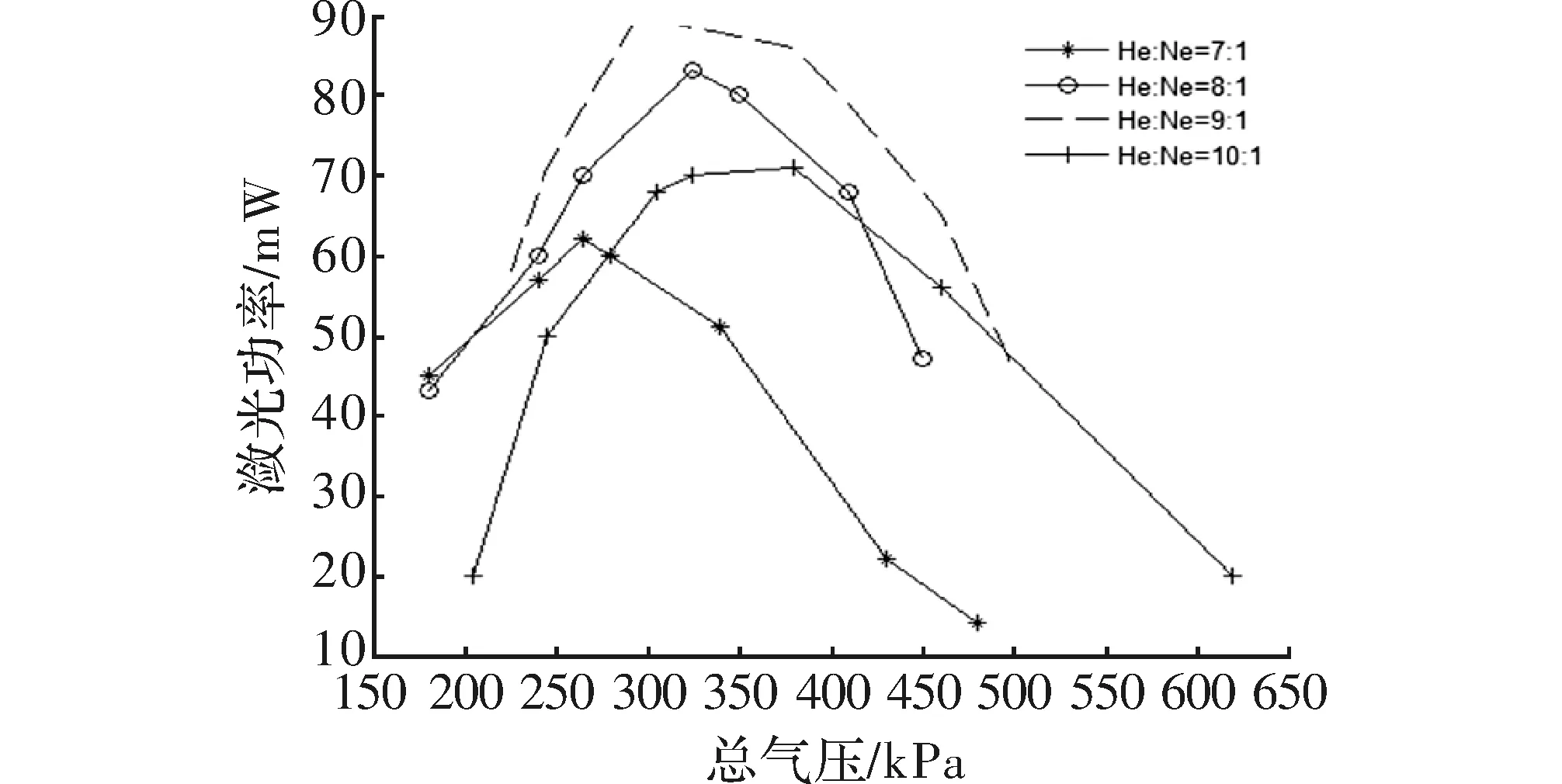
图1 激光输出功率与He-Ne气压、气比关系
可见,环形激光器中气体压强的变化不能忽略不计,气体压强的变化将引起环形激光器输出功率的变化。在实际工作中发现,-40 ℃时的输出信号强度是70 ℃时的 ,显然陀螺的信噪比发生了变化,从而引起零偏误差。
1.2 温度对激光陀螺结构参数的影响
(1)随着温度的升高,环形激光器的外围组件,如:光电探测器、全反射棱镜、抖动杆、压电陶瓷片以及加热器软管等都会发生相应的形变。由硅橡胶固定的光电探测器随着温度的变化有可能引起位置的偏移或旋转,这样由光电探测器输出的两路信号可能幅值相差很大,相位差超出规定的范围,引起计数或鉴相误差。温度的升高使全反射棱镜的折射率增大,引起光学程长增大,此时需要快速减小加热器电压,达到稳程长的目的,不过加热器属于大惯性环节,稳程长需要很长时间,故变温条件下程长很难稳定[8]。抖动杆和压电陶瓷片组成抖动机构,温度变化使抖动杆在高低温下的固有频率发生变化,且压电陶瓷片在高低温下的驱动能力不一致,故变温下抖动的效果不一样,即引起光路变化的方向不一致。同时加热器软管热胀冷缩,会对谐振腔腔体造成不同程度的牵引,引起全温下偏频量不一致,导致光路变化,最终引起零偏误差;
(2)陀螺内部元件的材料不同,导致温度变化引起的形变不同。环形激光器主要由微晶玻璃和全反射棱镜组成,抖动装置则是由低膨胀合金加工而成,这两种材料的膨胀系数相差10倍,温度变化后,引起抖动装置与环形激光器之间的变化量不一致,相互之间产生一定的扭矩,从而使激光陀螺的输入轴发生偏移或旋转,在陀螺的安装基准与光学轴线之间形成误差,从而引起零偏误差;
(3)激光陀螺在总装过程中,部件与部件之间的连接大多是用各种不同的胶粘结,胶具有很强的热塑性,热胀冷缩。温度变化会使胶的收缩量与被粘部件的收缩量不一致,膨胀量与所粘零件的膨胀量不一致,使零件的装配位置发生改变,引起零偏误差。
2 零偏温补模型
2.1 温度点的选择
温度点选择是否恰当,将影响到所测温度能否反映整个陀螺的温度变化,最终直接影响补偿精度的优劣。
棱镜式激光陀螺由基座、谐振腔、光电探测器、压电引燃变压器、铝支撑罩、内外磁屏蔽罩等组件构成。其中谐振腔平板中心的温度近似反映整个谐振腔温度的变化,所以该位置放置一个温度传感器;氦氖气体通道的温度变化会使得气体总气压发生改变,而环形激光器的输出功率与氦氖气体的压强密切相连,所以温度的变化影响激光输出功率,最终影响光强进而影响激光陀螺的零偏,故在氦氖气体通道附近放置一温度传感器;稳频气体附近的温度影响该气体的折射率,使光路发生偏移,从而影响零偏,所以在该位置也放置一温度传感器;测空气的温度是为了构造陀螺光学本体与外界环境的温度梯度,因此在铝支撑罩顶部空气中放置一温度传感器。
故采集的温度点如图2所示,图中:①为谐振腔平板中心(T1);②为氦氖气体通道附近(T2);③为稳频气体附近(T3);④为悬挂在内支撑罩顶部中心的空气中(T4)。
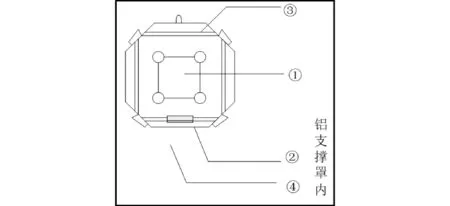
图2 温度采集点
2.2 陀螺零偏与温度的关系
控制温箱完成25 ℃→-40 ℃→25 ℃→70 ℃→25 ℃的温变过程,同步采集陀螺输出与陀螺温度,采样时间为100 s,由于4路温度的大体趋势基本相同,取T1作为代表,则零偏与温度的关系如图3所示。
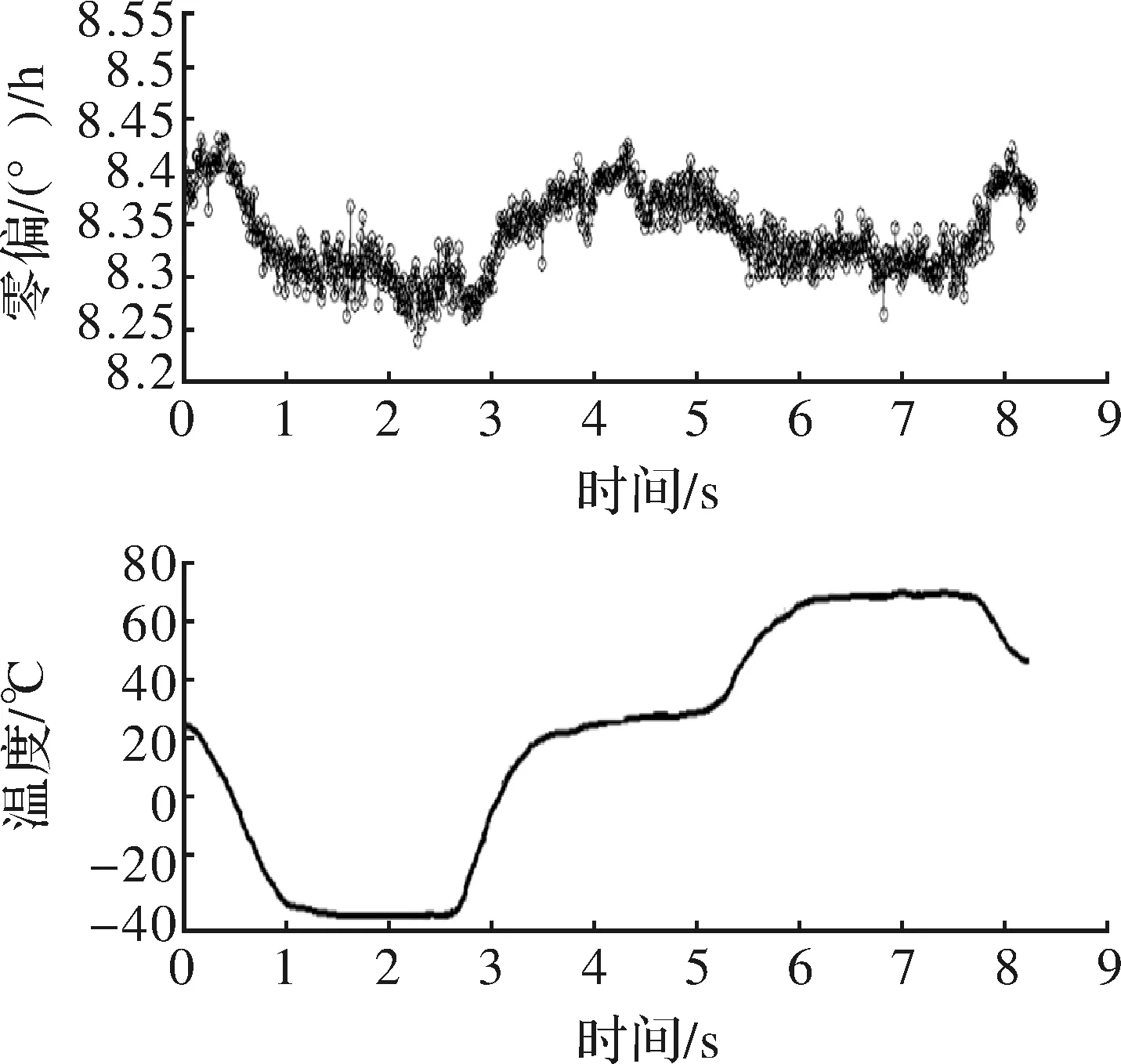
图3 零偏与温度的关系
如图3所示,陀螺零偏与温度具有明显的相关性。25 ℃→-40 ℃降温过程中,零偏下漂;-40 ℃→25 ℃升温过程中,零偏上漂;25 ℃→70 ℃ 升温过程中,零偏下漂;70 ℃→25 ℃降温过程中,零偏上漂;且温度变化率越大,温度转折点的陀螺零偏突变越大,温度不变时,陀螺零偏比较平稳。
2.3 模型确定
在快速温变情况下,不仅要考虑到静态温度项,还要考虑到温度变化率和温度梯度的影响[2]。基于陀螺零偏与温度的曲线关系知,温度、温度变化率及温度梯度与陀螺零偏具有较强的相关性,在温度变化的转折点上陀螺零偏有明显突变,且变化方向具有一定的规律性,因此可以考虑建立基于温度、温度变化率、温度梯度及其交叉项的二阶零偏温度模型[9-12]。
由于在实际应用中难以安装两个以上的温度传感器,首先根据模型1选择出对零偏补偿效果最佳的温度检测点;然后根据模型2选择出对零偏补偿效果最佳的某两个检测点的温度梯度;最终确定两个最佳温度检测点。
模型1 含温度、温度变化率及其交叉项的二阶模型
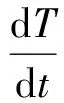
(1)
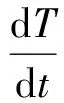
模型2 含温度、温度变化率、温度梯度及其交叉项的二阶模型
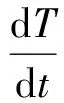
(2)

3 零偏温度误差辨识与补偿
3.1 试验方案
首先,选用西安北方捷瑞光电科技有限公司生产的棱镜式激光陀螺,将4个PT100温度传感器分别贴在上文所述的4个位置。控制温箱完成25 ℃→-40 ℃→25 ℃→70 ℃→25 ℃的一组温度循环,温变速率1,变温时间分别为6.5 h,6.5 h,6.5 h,3 h。同步采集陀螺脉冲数与温度,采样时间为100 s。共测试两组数据,分别记为A1和A2。再在-40~70 ℃之间,温度随机变化测试两组数据,记为A3和A4;
然后,将A1作为辨识数据,采用多元逐步回归法,分别对模型1和模型2进行不同温度检测点的参数辨识。设引入变量的显著性概率为0.05,剔除变量的显著性概率为0.2。得到模型决定系数R-square,最小均方误差RMSE[13-15]。
最后,用模型1、模型2及温度检测点数据分别对A2进行补偿,补偿前零偏稳定性记为S,补偿后零偏稳定性记为S1(即输出角速率与零偏的差的标准差),零偏稳定性提高百分比记为S2(即(S-S1)/S)。根据零偏稳定性提高百分比确定最佳温度检测点。
3.2 试验结果
3.2.1 模型1参数辨识及补偿
分别以T1、T2、T3、T4作为T,以A1作为辨识数据,通过逐步回归法进行参数辨识,对测试数据A2进行补偿,补偿结果如表1所示。

表1 模型1的不同温度检测点补偿
由表1可知,T=T3时补偿效果最好,所以确定T3作为T。
3.2.2 模型2参数辨识及补偿
基于模型1的结果,选择T3作为T,分别用T1-T3、T2-T3、T4-T3选作为ΔT,通过逐步回归法进行参数辨识,对测试数据A2进行补偿。补偿结果如表2所示。

表2 模型2的不同温度检测点补偿
由表2可知,T=T3和ΔT=T1-T3时补偿效果最好,所以确定T3作为T,T1-T3作为ΔT。
3.2.3 最佳温度检测点确定
比较上述两种模型的最佳状态,从中选出最佳温度检测点,各指标如表3所示。
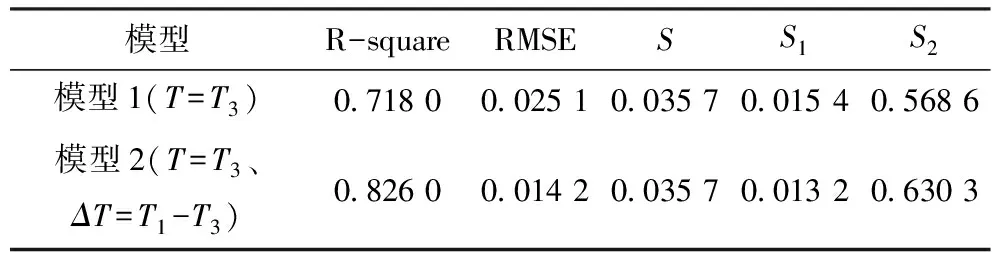
表3 两种模型最佳状态比较
从表3中可以看出,模型2(T=T3、ΔT=T1-T3)的R-square最大,RMSE最小,对补偿数据的零偏稳定性提高百分比最大,综合以上指标,确定最佳温度检测点为T1、T3两处,其中,T3作为温度;T1-T3作为温度梯度。
3.2.4 补偿结果分析
采用上述得到的最佳模型及最佳温度检测点,对A3、A4两组随机测试数据进行补偿,曲线如图4和图5所示,A3补偿前零偏稳定性为0.039 1,补偿后零偏稳定性为0.014 2,零偏稳定性提高63.68%;A4补偿前零偏稳定性为0.038 9,补偿后零偏稳定性为0.014 0,零偏稳定性提高64.01%。
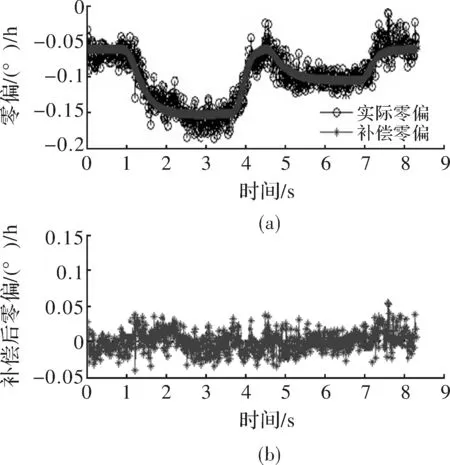
图4 补偿A3
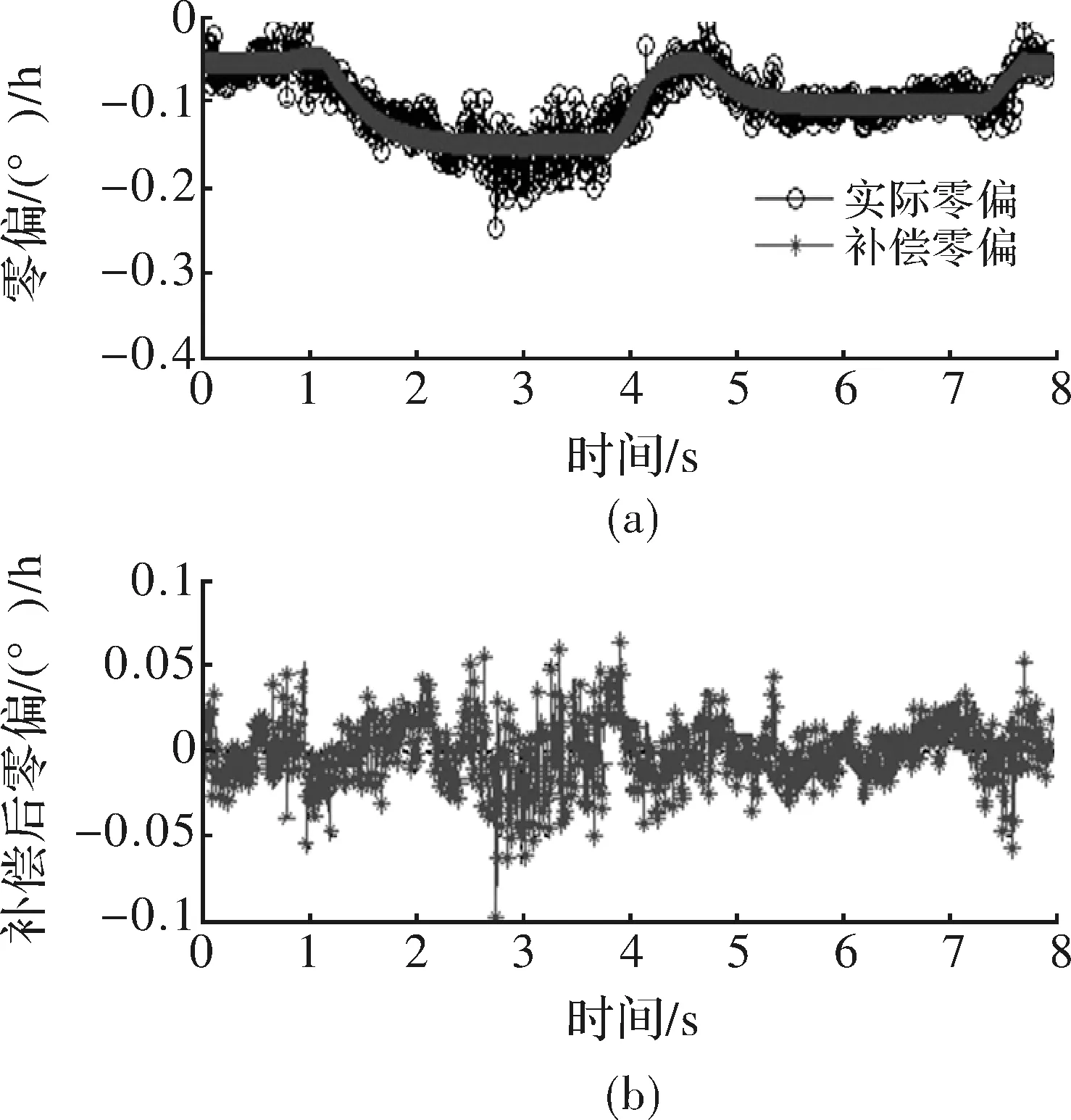
图5 补偿A4
从图4和图5可以看出,补偿零偏与实际零偏相似程度越高,补偿后效果越好,表现为补偿后零偏曲线波动性小,零偏值从正负趋于零。说明了温度检测点选择的合理性。
4 结束语
通过理论分析棱镜式激光陀螺的零偏温度特性,初步选择了对零偏影响较大的4个温度检测点,并通过试验得出陀螺零偏与温度、温度变化率及温度梯度相关性较强的结论。经过大量试验数据的分析处理,并用二阶动态温度模型对4个温度检测点进行优化选择,得出以谐振腔平板中心、稳频气体附近作为最佳温度检测点的结论。采用模型2对两组随机温变数据进行补偿,零偏稳定性提高60%以上。该分析结果为提高棱镜式激光陀螺的精度提供了参考。
[1] 赵东洋,石顺祥,李家立.全反射棱镜式环形激光器的温度效应[J].光子学报,2006,35(11):1627-1631.
[2] 周璐,任磊,刘晴晴,等.环形激光陀螺零偏热效应补偿模型的研究[J].传感技术学报,2013,26(3):353-356.
[3] 潘献飞,杨杰,吴美平.复杂温变环境下的激光陀螺零偏补偿方法[J].中国惯性技术学报,2011,19(2):234-237.
[4] 张鹏飞,王宇,汤建勋.机抖激光陀螺多温度点实时温度补偿方法的研究[J].兵工学报,2010,31(5):562-566.
[5] 郭创,张宗麟,王金林.激光陀螺温度特征点选择及其补偿[J].光电工程,2006,33(6):130-134.
[6] 徐文强.全反射棱镜式激光陀螺的零偏分析及温度补偿[D].西安:西安电子科技大学,2012.
[7] 赵小宁,李县洛,雷宝权.激光陀螺零偏温度补偿研究[J].中国惯性技术学报,2004,12(3):55-57.
[8] 刘健宁,刘继芳,石顺祥.全反射棱镜式激光陀螺腔长控制过程研究[J].电子科技,2010,23(7):32-35.
[9] 高伯龙,李树棠.激光陀螺[M].长沙:国防科技大学出版社,1984.
[10] 毛奔,林玉荣.惯性器件测试与建模[M].哈尔滨:哈尔滨工程大学出版社,2009.
[11] 张鹏飞,龙兴武.二频机抖激光陀螺零偏的温度特性的逐步回归分析[J].光学技术,2006,32(5):738-740.
[12] 刘明雍,周良荣,赵涛.激光陀螺温度误差补偿方法[J].鱼雷技术,2009,17(5):53-57.
[13] Sun Hongwei,Fang Jiancheng,Li Jianli.Temperature errors modeling for micro inertial measurement unit using multiple regression method[C].Qingdao,China:Proceedings of the International Symposium on Intelligent Information Systems and Applications,2009.
[14] Wu G,Gu Q.Thermal characteristics and thermal compensation of four frequency ring laser gyro[C].Wuhan,China:IEEE Position Location and Navigation Symposium,2002.
[15] 严恭敏,李四海,秦永元.惯性仪器测试与数据分析[M].北京:国防工业出版社,2012.
Zero Bias Compensation of Multiple Temperature Points of the Prism Laser Gyro
HE Xiaoli1,TAO Yuanbo1,2
(1.Xi’an North Jierui Opto-Electronics Technology Ltd., Xi’an 710111, China;2. School of Automation, Northwestern Polytechnical University, Xi’an 710129, China)
The optical path of the prism ring laser gyro is different from that of the reflector ring laser gyro in that quite long optical path is through the prism, so the temperature has an effect on zero bias. This article analyzes the characteristics between zero bias of prism laser gyro and temperature, and studies the relationship between the zero bias and the temperature, temperature change rate and temperature gradient. A multi-point second-order dynamic temperature model in complex temperature environment is established, with the two temperature measuring points for great contribution to gyro’s zero bias optimized and the random temperature variable data compensated. Results show the multi-point second-order dynamic temperature model can better compensate the zero bias’s variety introduced by complex temperature variety, with bias stability improved by more than 60%.
prism; laser gyro; optical path; temperature measuring point; compensation
2016- 07- 09
何晓莉(1981-),女,工程师。研究方向:光电子技术等。陶渊博(1990-),男,博士研究生。研究方向:仪器科学与技术,激光陀螺等。
10.16180/j.cnki.issn1007-7820.2017.06.039
TN249;TP241;U666.1
A
1007-7820(2017)06-138-04
