UKF在空中多平台多传感器数据配准中的应用

高晓利

(四川九洲电器集团有限责任公司 系统部，四川 绵阳 621000)



UKF在空中多平台多传感器数据配准中的应用

高晓利

(四川九洲电器集团有限责任公司 系统部，四川 绵阳 621000)

针对多传感器数据配准误差难以估计的问题，基于扩展卡尔曼滤波的基本思想，将目标运动模型和传感器配准误差模型组合在一个状态方程中，研究了扩展维度后的观测向量与状态向量间的关系，构造了简化的观测矩阵，在此基础上，利用扩展卡尔曼滤波方程对三维坐标系下配准误差进行估计，解决了配准误差难以估计的问题。数值试验表明，该方法能在有效估计目标运动状态的同时，估计出目标的传感器的配准误差，且算法复杂度较低、可实现性强。

数据配准；随机误差；配准误差；观测矩阵；扩展卡尔曼滤波

在多目标多传感器跟踪系统中，传感器配准是航迹关联、目标跟踪、数据融合、目标识别获得良好结果的前提，未经配准的传感器组合可能会导致系统性能比单一传感器还差，甚至当仅有一个目标存在时，也会使跟踪系统产生多个目标的错误信息。

传感器配准指多传感器数据“无误差”转换时所需要的处理过程，一般主要包括时间配准[1-2]和空间配准[3-4]两方面。所谓时间配准就是关于同一目标的各传感器不同步的量测信息同步到同一时间。所谓空间配准，又称为传感器配准，就是借助于多传感器对空间共同目标的量测对传感器的偏差进行估计和补偿。

近几年，诸多专家学者在传感器配准方面做出了杰出的贡献，提出了许多经典算法，如多假设跟踪，主要思路有3种：一种是离线方法，典型的做法是采用成批加权最小二乘方法求取误差参数[3]；第二种方法是放宽假设条件，利用卡尔曼滤波、扩展卡尔曼等在线估计误差[5-9]；最后一种是试图同时解决目标状态估计和系统偏差的估计[10-13]，文献[9]仅以空中平台的二维位置为研究对象，而二维位置不能准确描述目标的运动状态，文献[11～12]算法需较多的先验信息，并且算法的复杂度较高，因此，本文以时间配准成功为前提条件，重点研究三维坐标系下空中多平台多传感器的配准误差估计问题。

基于同时解决目标状态和系统偏差的估计的思想，以两个空中移动平台的多传感器配准问题为对象，研究了在三维坐标下扩展卡尔曼滤波在空中多平台的多传感器配准误差估计与目标跟踪问题。首先简单介绍了空中移动平台配准误差估计及跟踪所用的三维坐标系及其相互转换公式，其次将目标运动模型和传感器非线性测量模型组合在同一个状态方程中，研究了观测向量与系统向量之间的关系，构造了简化的观测矩阵，利用扩展卡尔曼滤波同时估计出目标状态和传感器配准误差。仿真表明，该算法能够较好地估计出目标的运动状态并给出传感器3个维度的配准误差。

1 预备知识

当传感器对目标坐标参数进行测量时，所得的参数数据总包含有两种随机误差和系统误差两种[11]。另外，数据配准算法还涉及笛卡尔坐标和极坐标之间相互转换。

1.1 随机误差

随机误差，也称为测量误差，在每次测量时，它都可能是不同的，这个误差是无法修正的。如雷达通过测量发射脉冲与收到的目标回波的时延测量目标的距离时，由于目标回波在传播过程中被噪声、杂波等调制，回波的相位就会发生变化，其变化程度与噪声和杂波的强度有关，同时考虑雷达本身的测量精度，得到目标时延与真实值之间存在着一个差值，这个差值就是测量误差/随机误差[11-17]。例如，目标真实距离为1 km，由于随机误差的存在，测量目标距离可能就是1±0.02 km。

1.2 系统误差

系统误差，也称为固定误差，其值不会随着测量次数的变化而变化，且通过校正是完全可以消除的。以预警机雷达观测目标为例，系统误差包括预警机雷达距离测量中的零点偏差、高度计零点偏差、由于采用某种信息处理方法而产生的方位误差等[10]。

1.3 笛卡尔坐标和极坐标相互转换

假设空中某点p的笛卡尔坐标为(x,y,z)，极坐标为(r,θ,φ)，如图1所示，则它们之间的关系方程式为

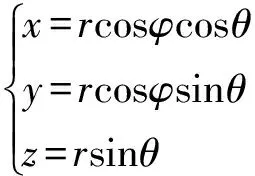
(1)

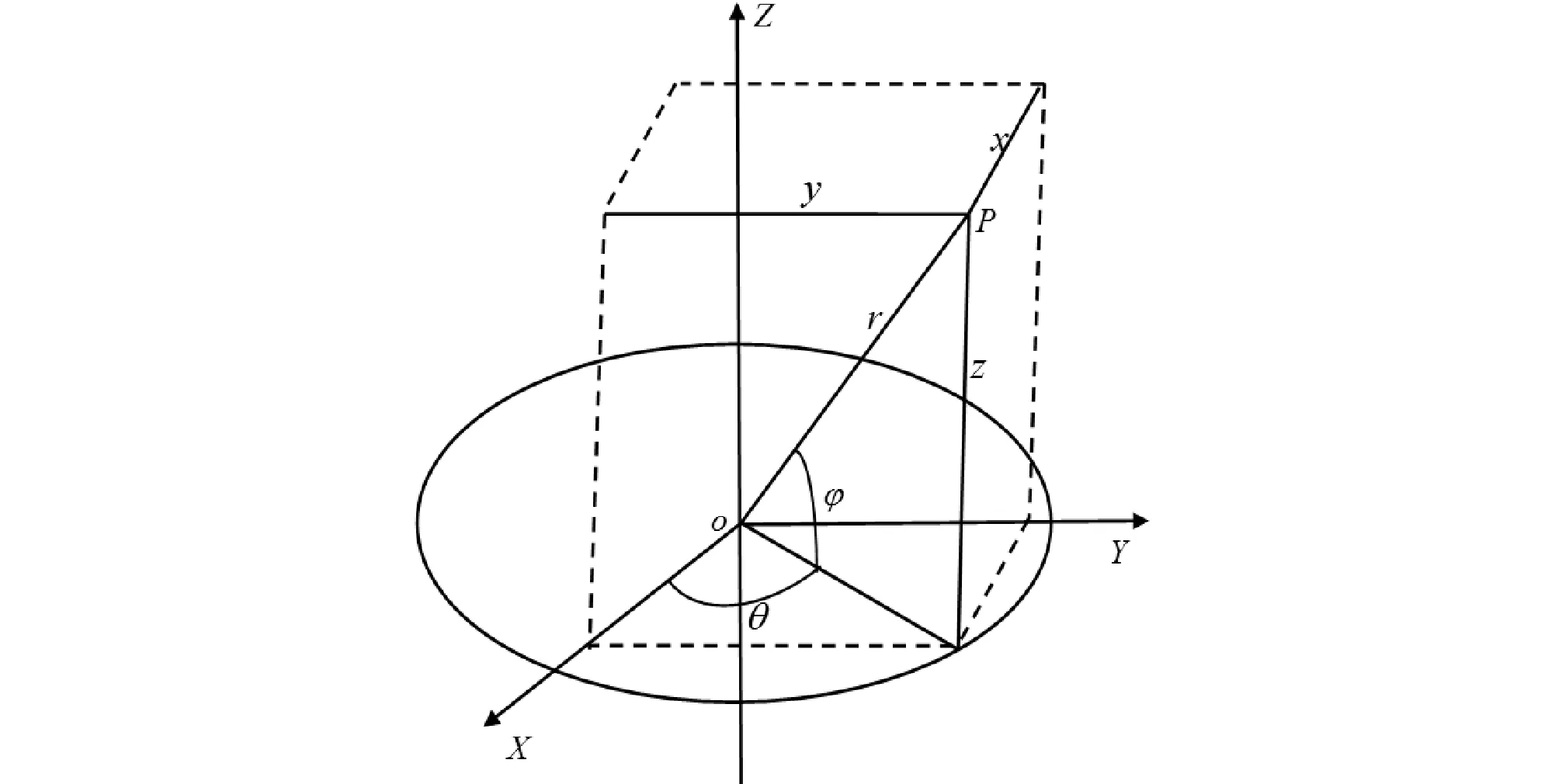
图1 笛卡尔坐标系和极坐标系

2 空中移动平台的坐标变换

假设传感器A和B分别位于不同的平台上。不失一般性，假设传感器A位于坐标原点(在地球坐标系中，坐标原点的位置一直在变化)，k时刻传感器B相对于传感器A的位置为[u(k),v(k),w(k)]，目标标记为Tk，如图2所示。

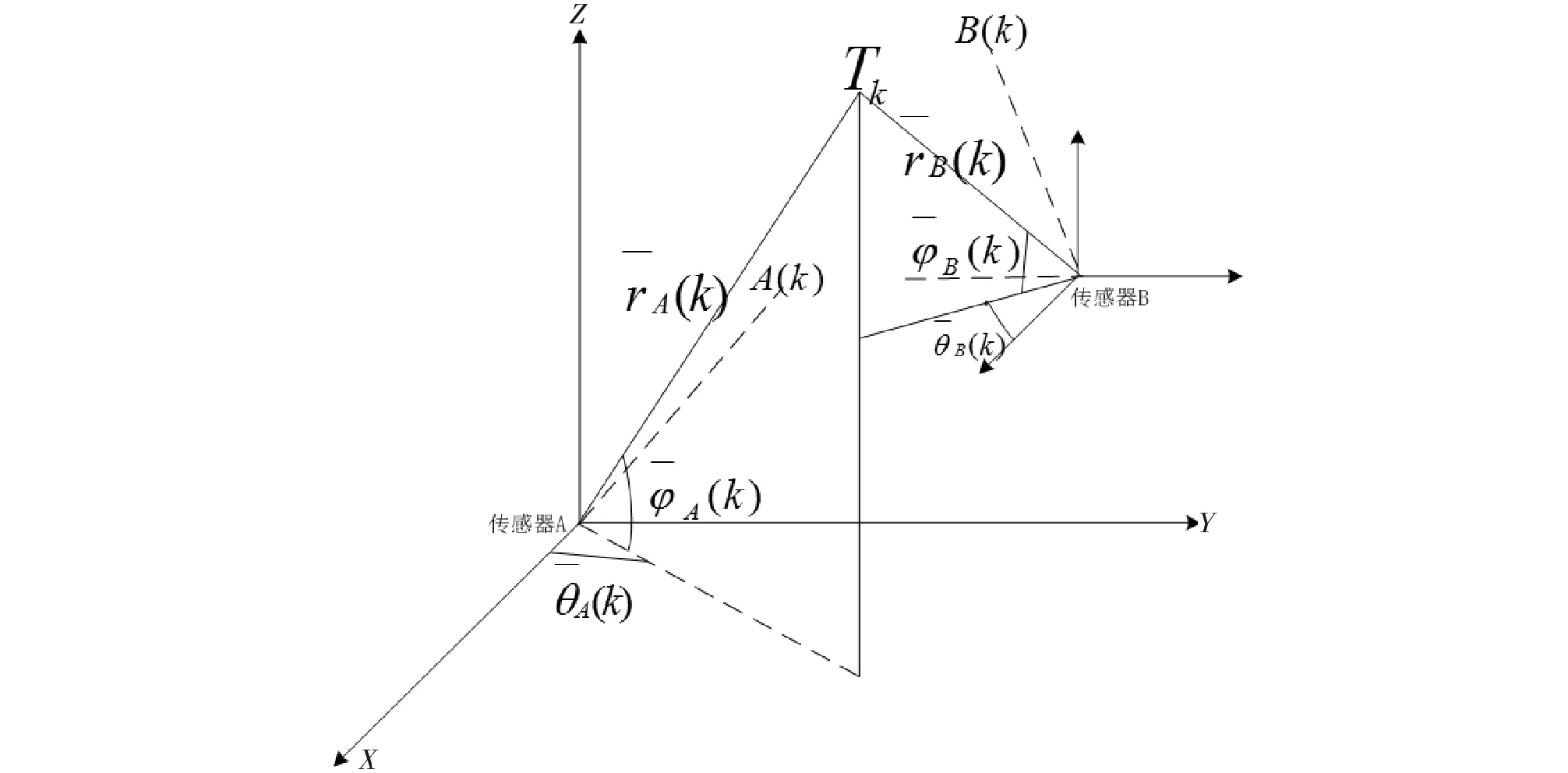
图2 配准误差的几何关系图

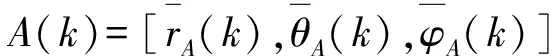
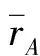
(2)

同理，xB(k)，yB(k)和zB(k)求解方法和式(2)相同，其中，ni(k)均为零均值正态分布的随机误差，i=1,2,…,6。

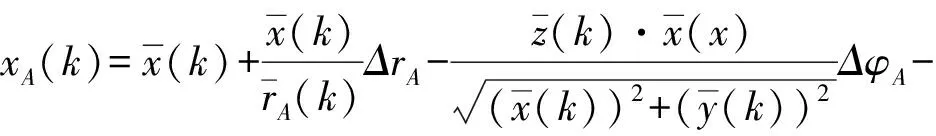
(3)

定义x1(k)=[xA(k),yA(k),zA(k)]T，x2(k)=[xB(k),yB(k),zB(k)]T，将式(3)写成矩阵形式

(4)

式中，A1(k),b1(k),ω1(k),A2(k),b2(k),ω2(k)分别可表示为

3 目标和传感器的动态方程

3.1 目标离散时间内的CV模型

ξ(k+1)=Φξ(k)+Γω(k)

(5)

式中

T为采样周期；Φ为状态转移矩阵；Γ为系统噪声系数矩阵；ω(k)为相互独立的零均值正态分布随机噪声。

3.2 传感器B相对于传感器A的动态模型

下面对后续用到的向量做以说明，假设定义ξ(k)=[u(k),Vu(k),v(k),Vv(k),w(k),Vw(k)]，[u(k),v(k),w(k)]为k时刻传感器B相对于传感器A的位置，[Vu(k),Vv(k),Vw(k)]为k传感器B相对于传感器A的速度，因此，传感器B相对于传感器A的二阶CV模型为

ξ(k+1)=Φξ(k)+ΓΨ(k)

(6)

式中，Ψ(k)为相互独立的零均值正态分布随机噪声。

3.3 传感器A对传感器B的测量方程

定义x3(k)=[xr(k),yr(k),zr(k)]为传感器A测得的传感器B的位置，则测量方程为

x3(k)=Mξ(k)+n(k)

(7)

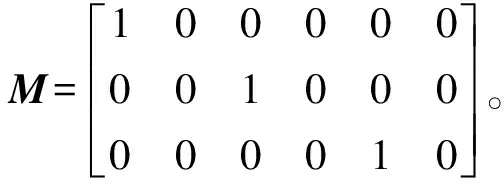
4 扩展卡尔曼滤波配准算法

x(k+1)=Fx(k)+nq(k)

(8)

式中

(9)

结合式(4)和式(5)，可以得出观测向量和系统向量的关系为

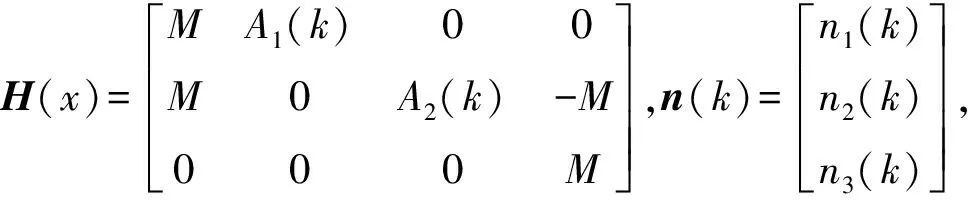
z(k)=H(k)x(k)+n(k)

(10)

因此，系统的状态方程和测量方程为

(11)

最后利用扩展卡尔曼滤波公式对式(11)进行估计，并同时估计出传感器的配准误差。扩展卡尔曼滤波的具体过程如下

5 数值试验

为验证算法的有效性，进行了蒙特卡洛计算机仿真，仿真条件如下：假设传感器A、传感器B和目标Tk均做均速直线运动，采样周期为1 s，时间长度为2 000 s，位置单位为km，速度单位为km/s，在直角坐标系中，传感器A的初始位置为(5,5,5)，速度vA为(0.05,0.15,0.1)；传感器B的初始位置为(30,10,20)，速度vB为(0.15,0.1,0.15)；目标Tk的初始位置为(15,45,30)，速度vA为(0.25,-0.1,0.25)；传感器A的距离、方位角、俯仰角的配准误差分别为ΔrA=41 m，ΔθA=0.0265 rad，ΔφB=0.01rad，传感器B的距离、方位角、俯仰角的配准误差分别为ΔrB=50 m，ΔθB=0.035 rad，ΔφB=0.02 rad；则传感器B相对于传感器A的相对速度为(0.1 km/s,-0.05 km/s,0.05 km/s)。

在直角坐标系下，X轴、Y轴、Z轴方向上，目标观测值与系统值、滤波值与系统值间的误差协方差关系如图3所示，由此可以得出，该算法可以较好地估计目标的运动状态。

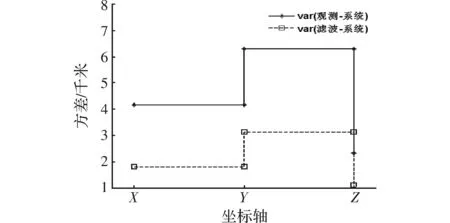
图3 误差协方差对比图

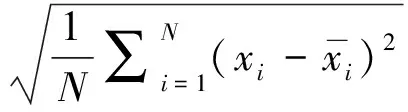
图4 传感器配准误差图

6 结束语

本文提出了将扩展卡尔曼滤波算法用于多平台多传感器的数据配准的应用，相对于传统算法，构造了扩展维度后的系统状态方程，建立了观测向量和状态向量之间的关系，简化了观测矩阵，实现了扩展卡尔曼滤波对配准误差的估计，仿真结果表明算法可操作性高、复杂度较小、并且3个维度方向的配准误差估计值均收敛于真实值，从而说明了算法的有效性。

[1] 石章松，刘忠.目标跟踪与数据融合理论及方法[M].北京:国防工业出版社,2010.

[2] 韩崇昭,朱洪艳,段战胜,等.多源信息融合[M].北京:清华大学出版社,2006.

[3] Zhou Y,Leung H.An exact maximum likelihood registration algorithm for data fusion[J].IEEE Transactions on Signal Processing,1997,45(6):1560-1569.

[4] Zhou Li, He You, Zhang Weihua. A new threshold of two-stage data correction algorithm for three-passive-sensor location System[C].Beijing:1st International Symposium on systems and Control in Aerospace and Astronautics, 2006.

[5] Li Dong Wei, Xie Wei Xin, Huang Jian Jun,et al.Space registration algorithm based on UKF using hybrid states[C]. Xi’an:ICSP2010 Proceeding,2010.

[6] 胡洪涛,敬忠良,胡士强.一种基于Unscented 卡尔曼滤波的多平台多传感器配准算[J].上海交通大学学报,2005,39(9):1518-1521.

[7] 王景伟,董大伟,华春蓉,等.扩展卡尔曼滤波的影响分析[J].电子科技,2016,29(8):10-12.

[8] 贺宏洲,秦玉峰,杨渝波,等.目标跟踪的转换量测卡尔曼滤波算法性能分析[J].电子科技,2016,29(5):112-116.

[9] 徐毅,陈非,敬忠良,等.基于扩展Kalman滤波的空基多平台多传感器数据配准和目标跟踪算法[J].信息与控制,2001,30(5):403-407.

参考文献

[1] 王鹏,魏守冰,黄青华.基于小波变换的自适应滤波器消除脉搏基线漂移[J].中国医学物理杂志,2004,21(5):296-299.

[2] Li Q,Clifford G.Dynamic time warping and machine learning for signal quality assessment of pulsatile signals[J]. Physiol Measurem,2012, 33(9): 1491-1504.

[3] 韩庆阳,李丙玉,王晓东.一种同时消除脉搏信号中呼吸基线漂移和高频噪声的方法[J].中国医学物理学杂志,2014(3):5-6.

[4] 徐涛.人体脉象生理信息的提取与识别方法研究[D].济南:山东科技大学,2008.

[5] 贾澎涛,何华灿,刘丽,等.时间序列数据挖掘综述[J].计算机应用研究,2007,24(11):15-18.

[6] 朱元波.一种数据挖掘系统的研究与实现[J].电子科技,2013,26(3):99-101.

[7] 钱伟立,徐兰义,陈富裕,等.高斯函数分解法提取脉搏波特征[J].中国生物医学工程学报,1994,13(1):1-7.

[8] 房建方.时间序列分段线性表示及定性趋势分析方法的研究[D].兰州:兰州理工大学,2013.

[9] 蒋嵘.基于形态表示的时间序列相似性搜索[D].南京:中国人民解放军理工大学,2000.

[10] 李俊奎.时间序列相似性问题研究[D].武汉:华中科技大学,2008.

[11] 李慧.奇异值分解在时间序列中的应用[D].北京:北京交通大学,2009.

[12] 宋辞,裴韬.基于特征的时间序列聚类方法研究进展[J].地理科学进展,2012,31(10): 1307-1317.

Registration for Multiple Airborne Mobile Platforms and Sensors with Extended Kalman Filter

GAO Xiaoli

(System Department, Sichuan Jiuzhou Electronic Group Co. Ltd., Mianyang 621000, China)

The multi sensor data registration error is difficult to estimate. Based on the basic idea of extended Kalman filter, the sensor registration errors are incorporated into an augmented dynamic model. The relationship between observed vector and system vector is studied and observed matrix is constructed, on foundation of which the Kalman filter is used to estimate the registration errors, which resolves the difficult problem of registration error. Computer simulations show that system states and registration errors are effectively estimated with less complex algorithm and better implementability.

data registration; random error; registration error; observed matrix; extended Kalman filter

2016- 08- 02

国防预先研究项目(12100201)

高晓利(1983-)，女，工程师。研究方向：多目标跟踪等。

10.16180/j.cnki.issn1007-7820.2017.06.010

TN713

A

1007-7820(2017)06-034-06