基于太阳影子的视频物体定位技术研究
2017-06-26李艾鲜
李艾鲜,潘 伟
(西华师范大学 计算机学院,四川 南充 637009)
基于太阳影子的视频物体定位技术研究
李艾鲜,潘 伟
(西华师范大学 计算机学院,四川 南充 637009)
针对不同地理位置的物体及其时间变化问题,通过分析摄影测量学中影响物体太阳影子的因子建立数学模型。针对该模型在实际应用中的问题,以该模型为目标函数编写算法,确定物体的最优所在地和拍摄时间,并对两种算法的结果进行比对和实用性分析。结果表明,本模型能较好的计算视频中物体的地理位置和视频的拍摄时间。
摄影测量学;影子定位;人群搜索;优化问题
随着数字视频应用的日益广泛,基于视频数据的摄影测量越来越受到人们的重视。其中,确定视频中目标物体的拍摄地点和拍摄日期是摄影测量学中视频数据分析的基础。然而,传统的人工测量技术在实际应用中存在诸多局限性,且无法保证数据的精确性,因此在进行数据处理和数据分析后得到的结果存在较大误差。本文提出了一种基于太阳影子的定位算法,并针对其进行了以下3个部分的工作:一是分析了视频中太阳影子变化的特点;二是依据相应的数学模型设计了算法。三是通过实验,拟合实际数据和所解出的数据,探究了所建立模型的准确性,并分析了不同算法实现的利弊。
1 理论概述
本文假设太阳和地球均是质地均匀的球体,太阳照射地球没有阻碍,且太阳直射点在一天内直射的纬度不发生变化。太阳赤纬角[1]是地球赤道平面与太阳和地球中心的连线之间的夹角。其计算公式为
(1)
其中,n为时间,是以3月21日为初始零点,次年3月21日为终点,取值范围为[0,360]。
太阳高度角是指太阳光的入射方向和地平面之间的夹角。太阳高度角随地方时和太阳赤纬角的变化而变化,其计算公式为[2-3]
α=arcsin(sinφsinσ+cosφcosσcosω)
(2)
式中,φ为纬度;ρ为经度;ω为太阳时角。
目标物体影子长度L2关于经纬度、事件及直杆长度的函数关系式
(3)
目标物体太阳影子长度的实际值L1[4]

在实际操作中需要衡量经纬度的取值是否符合真实情况,因此将实际的影子长度L1和求解出的影子长度L2作为参数,引入残差值Z,用残差值Z和多组实际数据与计算数据的拟合曲线来综合评估模型。残差值计算公式如下
Z=(L1-L2)2
(4)
由式(1)~式(4)建立模型
(5)
在实际应用中,视频是连续拍摄的。其数据量较为巨大,存在多个L1值。所以引入总残差值的概念。其计算公式如下
(6)
在一组经纬度取值下遍历完一组(x0,y0)值,便可得到一个Zs,找出所有取值中最小的Zs,与之对应的经纬度和时间就是该视频拍摄地点的经纬度与时间。最后联立式(4)和式(5)建立模型
(7)
2 算法
2.1 遍历搜索算法
遍历搜索是遍历目标物体所处的地点和所在地时间。输入给定的物体影子坐标,以此遍历经纬度、时间及物体高度。本次实验中以地面为参考系建立空间直角坐标系,已知影子顶点坐标和拍摄时间,在杆长未知的情况下,求解其经纬度、高度和视频拍摄日期。其具体算法实现如下:
1 x0,y0;%载入数据
2 b=1:90; %纬度
3 r=1:180;%经度
4 day=1:365;%日期
5 TT1=(12+41/60):(3/60):(13+41/60);%校正时差
1zS0=inf,b0=0;r0=0,day0=0;%初始化参数
2 for i=1:21
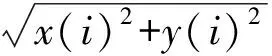
4 End
5 max1=2*max(L1);%取最大影子长度的两倍为杆长的最大可能值
6 h=0:0.5:max1;%直杆长度以0.5为步长
7 forb=1:1:90%以1为步长
8 forr=1:1:180%以1为步长
9 for k=1:length(h)
10 for H=1:21%计数
11 Z=0;%初始化残差值的中间变量
12 for day=0:15:365%以15为步长遍历搜索
13 L2=func(day(D),TT1(H),r(b),b(r),h(k));%带入参数计算影子长度
14 Z=(L2-L1)2;Zs=Zs+Z;%计算残差值和总残差值
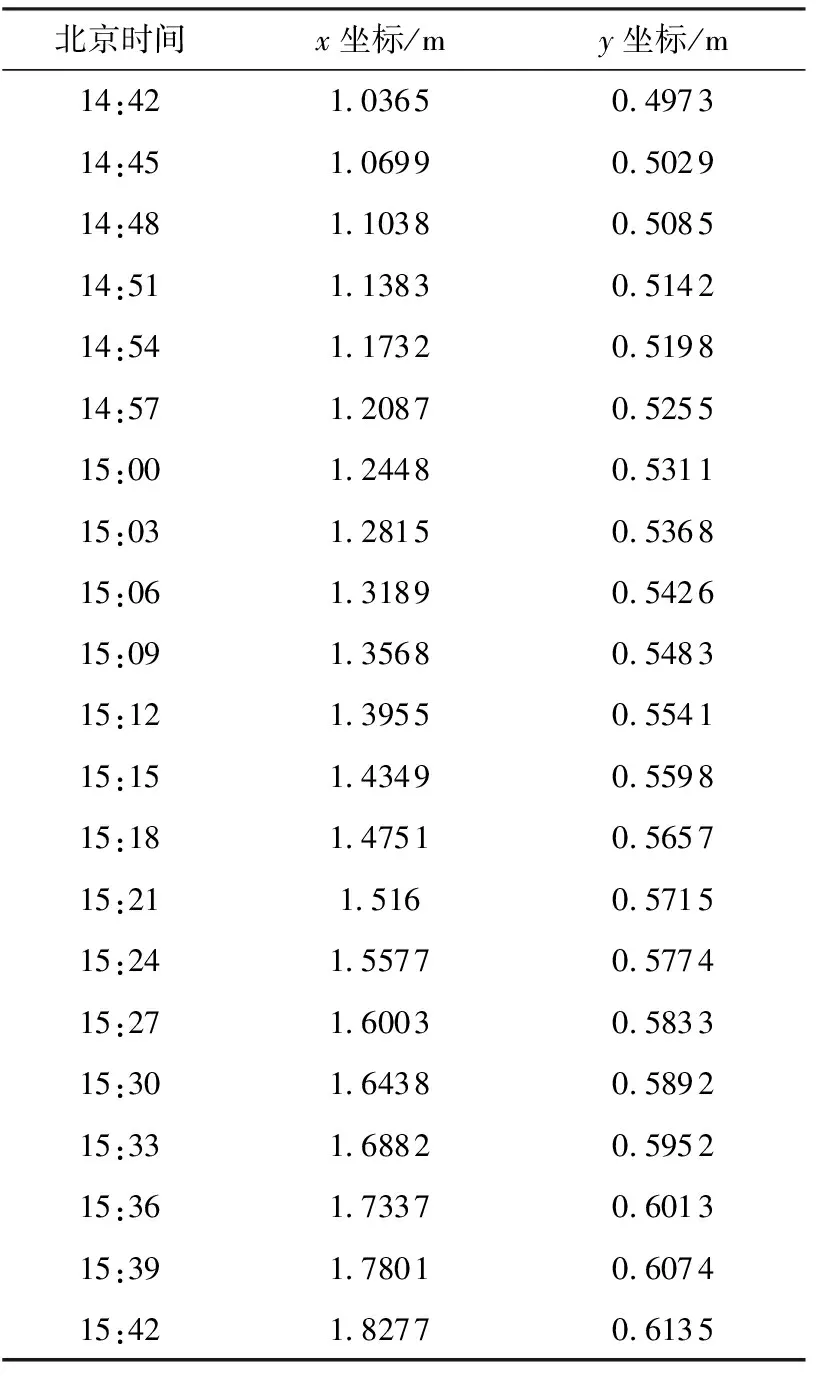
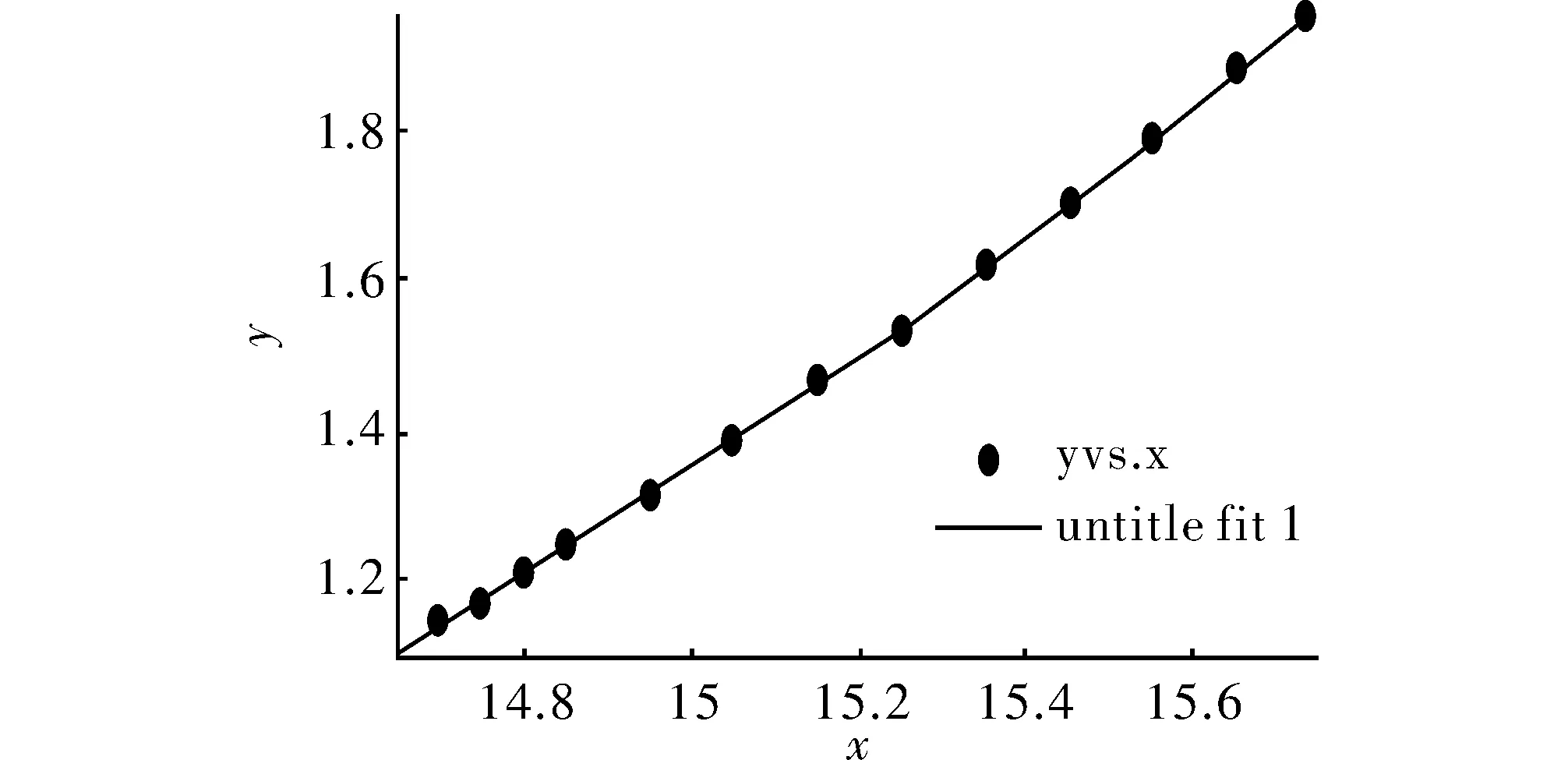
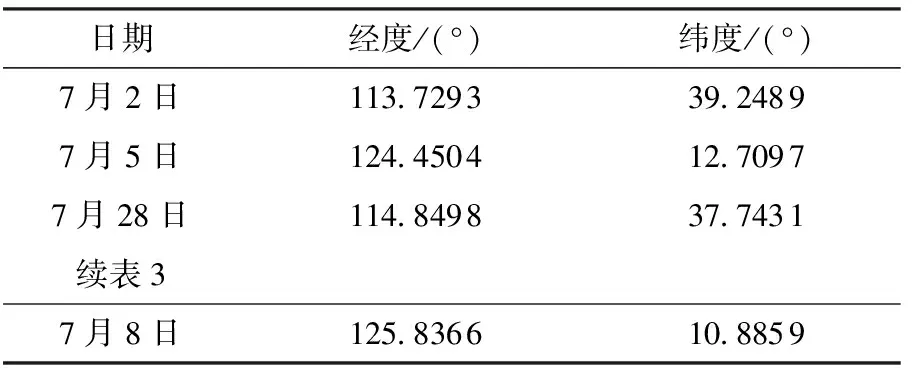
15 If Zs 16 Zs=Z0;b0=b;r0=r;day0=day;k0=k; 17 end 18 end 19 end 20 end 21 end 22 输出b0,r0,day0 %b0为最优纬度,r0位最优经度,day0为最优日期 本次实验在编程求解目标物体的所在地和时间。所得的时间day0为天数,对其进行简单的化解即可得到目标物体所在地的日期。但该程序运行时间至少4 h,不利于实际应用。 2.2 人群搜索算法 由于遍历搜索在最坏情况下的时间复杂度O(n4),耗时长,效率低。因此,考虑改进算法。 人群搜索算法(SOA)[5]是模拟人的随机搜索行为,将人的智能搜索行为直接应用于对于优化问题的搜索。在优化计算中可对随机搜索行为进行模拟,得到经验梯度,然后确定一个方向进行搜索。当搜寻者所处位置较优时,应在较小领域内搜索;当搜寻者所处的位置较差时,应在较大领域内搜索。因此,SOA利用能有效描述自然语言和不确定性推力的模糊逻辑来对上述搜索规则进行建模并确定搜索步长[6-9]。其具体实现如下: 步骤1 基本参数初始化。设置人群搜索的种群规模size=pop、最大进化次数maxgen、速度限制上下线参数Vmax和Vmin; 步骤2 人群初始化。在可行解域内随机初始产生sizepop初始位置,此时进化代数为t=0。其式如下 (8) 其中,i=1,2,3,…,sizepop,t=0; 步骤3 适应度函数的选取。在人群搜索算法中,适应度函数用来评价个体的优劣,引导程序按照提高精度的方向不断进化。在本文中,适应度函数采用总残差为目标函数。根据实际情况,计算每个初始位置的目标函数值,并取得当前最优值; 步骤4 搜索步长。SOA算法通过模拟人的智能搜索行为,建立目标函数和步长之间的联系。这其中的模糊规则描述如下:目标函数越小,则搜索步长越小。定义搜索步长的模糊变量函数为高斯隶属函数,其式如下 uA(x)=e (9) 当输出变量超出[u-3σ,u+3σ]时,若隶属度<0.011 1,则可以忽略,故一般设定umin=0.011 1。这里采用线性隶属度函数,隶属度与函数值排列顺序成正比,出于最佳位置的搜寻者具有最大值1,最差位置为0.011 1。对于其他位置,u<1.0,如下式 uij=rand(ui,1),j=1,2,3,…,D (10) ui为目标函数值i的隶属度;uij为j维搜索空间目标函数i的隶属度;在得到隶属度后,可计算步长 (11) 其中,δij为高斯隶属度函数的参数,其式为 δij=w·abs(xmin-xmax) (12) 其中 (13) xmin和xmax为种群中具有最小和最大函数值的位置;w是惯性权值,随着进化代数的增加从0.9线性递减至0.1;itmax和it分别为最大迭代次数和当前迭代次数。 步骤5 位置更新。确定搜索方向和搜索步长之后,对每个群体内的个体进行位置更新,更新公式如下 Δxij(t+1)=aij(t)dii(t) (14) Δxij(t+1)=xij(t)+Δxji(t+1) (15) 步骤6 进化一代,t=t+1; 步骤7 若满足终止条件,则停止搜索。否则,转至算法的第3步。 将本文建立的模型作为目标函数,编程实现该算法。人群搜索算法可设定问题规模,因此求出多组解绘制其散点图即可得到相对最优解。运行结果表明,使用人群搜索算法,可大幅降低计算的时间复杂度。 3.1 模型检验 该模型以太阳赤纬、目标物体高度、目标物体经纬度以及拍摄时间为参数,计算出目标物体的影子长度。为了验证模型的合理性,在已知摄影地点、目标物体高度、拍摄时间以及目标物体在拍摄时间内的影子长度变化情况。实际测量的影子顶点坐标如表1所示。 表1 测量的直杆影子定点坐标 该组数据是坐标系以直杆底端为原点,水平地面为xy平面,直杆垂直于地面,测量日期是2015年4月18日。 使用该模型为目标函数编程求解出,该段时间内目标直杆的太阳影子随时间变化的规律。利用计算机编程拟合出目标物体在24 h内的太阳影子长度变化曲线,如图1所示。 图1 太阳影子长度随时间变化的曲线 将计算出的该段拍摄时间(14:00~16:00)内的影子长度变化与实际测量数据进行拟合,其拟合曲线如图2所示。 图2 拍摄时间内计算数据与实际数据的拟合曲线 从图2易观察到拟合度良好。因此说明,该数学模型可较好的拟合太阳影子长度与时间之间的关系。此数学模型是本技术的基础。利用该模型及从摄影视频中提取的影子长度数据,利用计算机编程可以反解出摄影视频中目标建筑所在的拍摄地以及所拍摄的时间。 3.2 影子定位技术应用 用计算机提取到在内蒙古呼伦贝尔市录制的一段视频中,某一固定直杆的太阳影子定点坐标数据,如表2所示。 表2 视频中固定直杆的影子长度 假设日期、地点未知。因遍历搜索算法在运行4 h后也未能成功搜寻到结果,所以使用SOA算法,搜索结果如下。 表3 人群搜索算法结果 通过对比实际情况,得知SOA算法可较好的解出较为接近真实情况的结果,但并不能得到最优解。 3.3 误差分析 在建立数学模型时,因实际计时是以地球在轨道上绕太阳做匀速运动,但实际上地球绕太阳做变速运动,所以需要矫正真太阳时与平太阳时之间的误差[10-12]。从实际测量数据与模型拟合数据进行拟合得到的拟合曲线,如图2所示,模型拟合度良好,由此说明该模型具有较好的实用性。 通过多次实验,并将多次实验的测量数据与计算数据分别进行统计和拟合,可知由该模型为目标函数编写程序实现算法,可较精确的计算出视频中目标物体所在地和拍摄日期[13]。针对遍历搜索算法,通过实验与实际数据相比较,其解出结果较为精确,但程序运行时间长,效率较低,实用性较差。针对人群搜索算法,其解出的结果精确度不够理想,多组解中的某些解与真实值可能存在较大误差。但其程序运行时间短,几乎可以做到实时处理,实用性优良。 本文研究摄影影像学中物体之间的太阳影子变化的规律,建立数学模型探究了太阳影子在不同时刻、不同经纬度以及不同物体高度的变化关系。在实际应用中,首先应用该模型识别地域信息。其次,可将其应用于优化建筑物在不同经纬度的房屋采光设计、楼间间距等。最后,应用该技术优化摄像机照相机位置定点,找寻最佳的摄影拍摄位置等。 [1] 陈晓勇,郑科科.对建筑日照计算中太阳赤纬角公式的探讨[J].浙江建筑,2011,28(9):6-8. [2] 中国气象局.地面气象观测规范[S].北京:气象出版社,2003. [3] 王国安,米鸿涛,邓天宏,等.太阳高度角和日出日落时刻太阳方位角一年变化范围的计算[J].气象与环境科学,2007,30(S1):161-163. [4] 王存良.电离层电子浓度计算模型中有关太阳参数的计算[J].中国电子科学研究院学报,2013, 8(1):86-90. [5] 蒋洪力.太阳直射点纬度的数学推导和分析[J].数学通报,2007(9):39-40. [6] 郑鹏飞,林大钧,刘小羊,等.基于影子轨迹线反求采光效果的技术研究[J].华东理工大学学报,2010,36(3):458-463. [7] 高飞.Matlab 智能算法超级手册[M].北京:人民邮电出版社,2014. [8] 单黎明.太阳跟踪定位技术及其应用研究[J].空间控制技术与应用,2012,38(3):58-62. [9] 史伟会.太阳自动跟踪系统研究[D].上海:东华大学,2011. [10] 郭芮.太阳光自主定位跟踪系统的研究[D].长春:长春理工大学,2012. [11] 郑小年,黄巧燕.太阳跟踪方法及应用[J].电力与能源,2003,24(4):149-151. [12] 刘路路,黄祥康,邱选兵,等.基于ARM的太阳跟踪控制系统设计[J].电子科技,2013,26(6):10-13. [13] 曹俊茹,李奎,宋振柏,等.大地纬度计算日影高度角方法[J],测绘通报,2012(8):58-59. Sun Shadow Positioning Technology in Photography LI Aixian,PAN Wei (School of Computer Science, China West Normal University, Nanchong 637000, China) By analyzing multi-element of sun shadow, we built a mathematical model that has model evaluation and model analysis through experiments. The model with objective function can be use the algorithm and programs. In order to determine the optimal solution to the location and the shooting time, the time complexity of the first algorithm should be under the consideration. We use a new programming algorithm for solving the location of objects in the image and the shooting time. Comparison of the two algorithms shows the superiority of the proposed model. photogrammetry; shadow location; soa; optimum seeking method 2016- 09- 02 李艾鲜(1994-),女,本科。研究方向:计算机应用。潘伟(1976-),硕士,副教授。研究方向:粗糙集等。 10.16180/j.cnki.issn1007-7820.2017.06.040 TN919.85;P288.4 A 1007-7820(2017)06-142-05
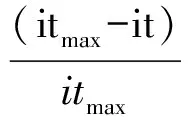
3 模型应用与检验


4 结束语
