倒向随机微分超前方程适应解的稳定性

周会会

广东海洋大学 理学院,广东 湛江 524088

倒向随机微分超前方程适应解的稳定性

周会会

广东海洋大学 理学院,广东 湛江 524088

本文研究了倒向随机微分超前方程（超前BSDE）适应解的稳定性问题，从理论上证明了在Lipschitz条件下超前BSDE的适应解具有稳定性。

倒向随机微分超前方程;适应解;稳定性

1 引言

Pardoux和Peng[1]引入了非线性倒向随机微分方程（BSDE），并证明了在Lipschitz条件下非线性BSDE适应解的存在唯一性。BSDE在随机控制、偏微分方程、数理金融、经济等领域都有着广泛的应用，吸引了众多学者对其研究[2-6]。

Peng和Yang[7]引入了一类新的倒向随机微分方程，即倒向随机微分超前方程（超前BSDE），形式如下：

其中δ（·）和ξ（·）是定义于[0，T]上取值于R+上的两个连续函数且满足下列条件(1)和(2)，

(1)存在常数K≧0K≥0，使得∀S∈[0,T]，有

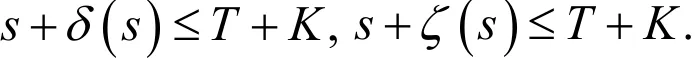
(2)存在常数L≧0L≥0，使得∀t∈[0,T]及非负可积函数g(·)，有

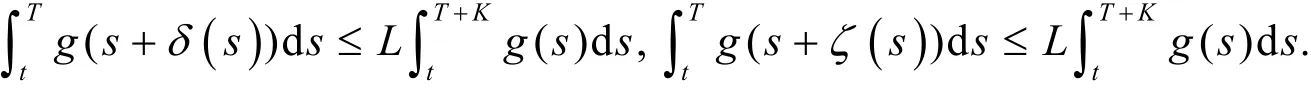
并证明了在Lipschitz条件下超前BSDE适应解的存在唯一性，参见引理1。

令(Ω,F,P)表示完备的概率空间，假设(W(t))t∈[0,T]是概率空间(Ω,F,P)中的d维布朗运动，{Ft}t∈[0,T]是由W产生的自然代数流。文中用到下面的概率空间，L2(Ft;Rd)表示Rd值的Ft-可测的随机变量且满足表示Rd值的Ft-适应的随机过程且满足表示中的连续过程且满足

引理1[7]设 f满足(H1)和(H2)，δ、ζ满足(1)和(2)，则对任意给定的终端条件超 前 BSDE(1)有 唯 一 解 ， 即 存 在 唯 一 一 对 F-适 应 过 程t满足方程(1)。

2 超前BSDE适应解的稳定性

Hu和Peng[8]中给出了BSDE适应解的稳定性定理，考虑到超前BSDE存在唯一适应解，下面来讨论超前BSDE适应解的稳定性。

考虑下面具有参数ε≥0的超前BSDEs，

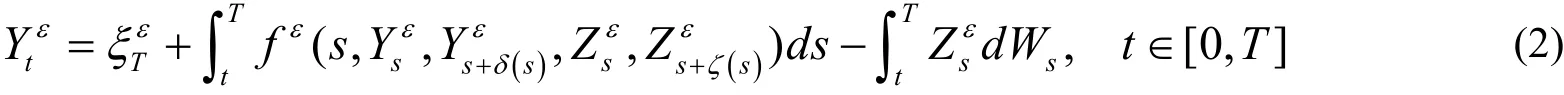
当ε→0时，我们做如下假设，

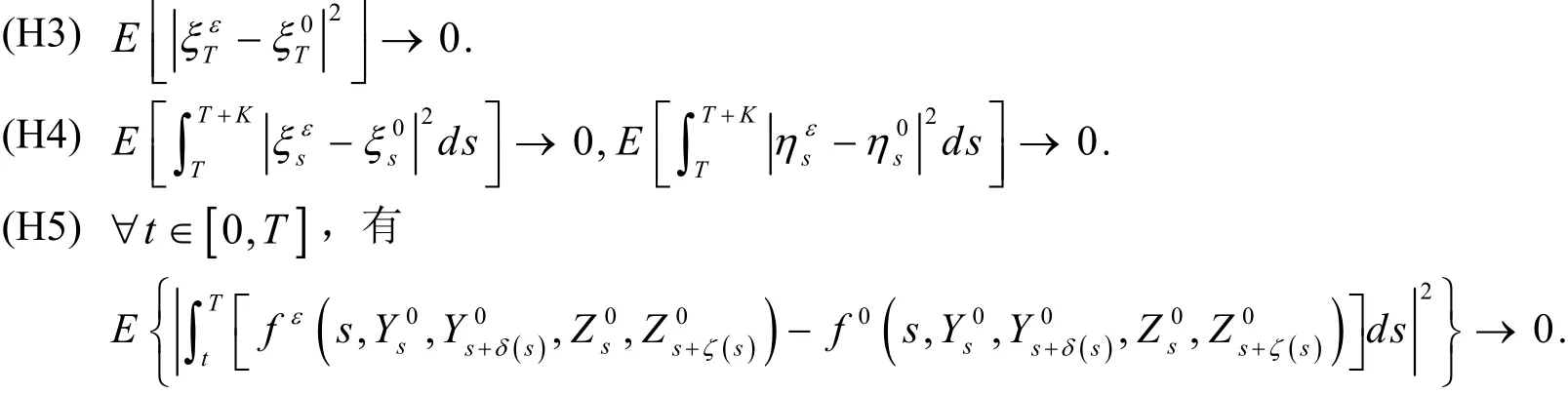
定理1假设超前BSDE满足(H3)，(H4)和(H5)，我们有

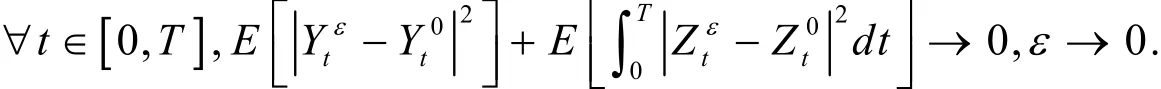
两边平方并取期望可得

从而由Gronwall不等式，可得

又由于方程(2)满足(H3)，(H4)和(H5)，从而Cε(t)在0≤t≤T上关于ε是一致有界的，因此特别地，当ε→0时，然后用同样的方法可证明在区间［T - 2δ,T -δ］，［T - 3δ,T - 2δ ］,…上结果亦成立。

3 结论

考虑到具有Lipschitz条件的超前BSDE存在唯一适应解，在此基础上，进一步研究了超前BSDE适应解的稳定性问题，从理论上得到了超前BSDE的适应解具有稳定性，对超前BSDE有了进一步的认识。

[1]Pardoux E,Peng SG.Adaptedsolutionof a backward stochasticdifferentialequations[J].Syst.Cont.Lett,1990,14(1):55-61

[2]Karouin El,Peng SG,Quenez MC.Backward stochastic differential equations in finance[J].Math.Fin,1997,7(1):1-71

[3]Lepeltier JP,San MJ.Backward stochastic differential equations with continuous coefficient[J].Stat.Prob.Lett,1997,32(4):425-430

[4]Liu JC,Ren JG.Comparison theorem for solutions of backward stochastic differential equations with continuous coefficients[J].Stat.Prob.Lett,2002,56(1):93-100

[5]Wang Y,Huang Z.Backward stochastic differential equations with non-lipschitz coefficients[J].Statistics and Probability Letters,2009,79:1438-1443

[6]Mao XR.Adapted solutions of backward stochastic differential equations with non-lipschitz coefficients[J].Stochastic Processes and their Applications,1995,58:281-292

[7]Peng SG,Yang Z.Anticipated backward stochastic differential equations[J].Ann.Prob,2009,37(3):877-902

[8]Hu Y,Peng SG.Astability theorem of backward stochastic differential equations and its application[J].Probability Theorey,1997,324(9):1059-1064

Stability of Adaptive Solutions for BackwardStochastic Differential Equations

ZHOU Hui-hui
College of Science/Guangdong Ocean University,Zhanjiang 524088,China

This paper focuses on the stability of adaptive solutions for backward stochastic differential anticipated equations (advanced BSDE).It is proved theoretically that the adaptive solutions of anticipated BSDE are stable under Lipschitz conditions.

Anticipated backward stochastic differential equations;adapted solutions;stability

O211.6

:A

:1000-2324(2017)03-0456-03

2015-05-15

:2015-09-06

广东省高校创新强校工程(2014KQNCX080)

周会会(1984-),女,硕士,讲师.主要从事金融数学、倒向随机微分方程的研究.E-mail:huihui0325@126.com