不同龄组华北落叶松人工林径向生长模型构建
2017-06-24张冬燕王冬至张志东黄选瑞
张冬燕,王冬至,张志东,黄选瑞
1.河北农业大学 商学院,河北 保定 071000 2.河北农业大学 林学院,河北 保定 071000
不同龄组华北落叶松人工林径向生长模型构建
张冬燕1,2,王冬至2*,张志东2,黄选瑞2
1.河北农业大学 商学院,河北 保定 071000 2.河北农业大学 林学院,河北 保定 071000
本文以塞罕坝不同龄组华北落叶松人工林为研究对象,以非线性单木胸径生长模型为基础模型,考虑主要立地因子及林分密度对不同发育阶段华北落叶松胸径生长量的影响,利用哑变量方法构建包含不同龄组林分竞争指数及主要立地因子的非线性混合效应胸径生长模型。结果表明:由立地因子与立木胸径生长量进行相关性分析,确定每公顷株数、海拔、坡向、土层厚度是影响华北落叶松人工林胸径生长主要限制性因子,相关系数分别为:0.67、0.51、0.54、0.38;在不同龄组由于经营水平和作业方式不同,林分平均竞争指数与龄组呈负相关关系,不同龄组林分平均竞争指数分别为:6.26、2.17、0.61;以不同龄组林分平均竞争指数为哑变量,构建了包含影响立木胸径生长主要因子的非线性混合效应模型,不同龄组模型BIC值分别为-142.3、-109.4、-94.7;AIC值分别为:-145.8、-129.5、-113.6;-2 Log Likelihood值分别为:-463.8、-147.5、-131.6。在不同立地条件下,混合效应模型中固定效应参数能够反映大多数立木胸径生长量随年龄的变化总趋势,随机效应参数能解释不同立木年龄和胸径生长曲线的变异。因此,非线性混合效应模型提高了对胸径生长量的预测精度及适用范围。
华北落叶松;人工林;立地因子;非线性混合效应模型;胸径
在森林经营管理与规划中,林分生长和产量模型经常被用来模拟和预测林分生产力及空间结构变化[1],其中林分生长是开展森林各项研究工作的基础,如气候对生长的影响[2]、林分生长对干扰的响应[3]、生长模型的建立[4]及预测林分产量[5]等。因此,从生态学和森林经理学的角度来讲,了解胸径生长过程具有重要意义。到目前为止,已有许多经验生长模型得到了发展与应用,如地位指数模型[6,7]、树高-胸径模型[8]、立地因子与树高关系模型[6]、断面积和林分密度模型[5]。然而,目前对立木胸径-年龄生长模型研究较少,对树高研究较多,主要是由于树高能够反映林分潜在立地生产力[6],而胸径生长模型作为森林生长和产量模型的一个重要组成部分,其分布不仅可以用来推断林分的演替阶段[9]及预测林分径阶分布动态变化[10],还是森林经营活动中各种经营技术的评价指标[11],此外在实际调查中胸径比树高更容易观测。因此,对胸径-年龄生长模型的研究更具有实用性。
单木生长模型能够精确描述林分结构和动态变化规律[11-13],在应用过程中具有更高的灵活性和精确性[14],并可以用来对林分不同培育措施和经营方法进行模拟和比较[15]。目前大多数单木胸径生长模型都是线性的,模型中都不包括立地因子[16,17],立木在生长过程中由于受到立地条件及经营模式等多种因素的影响,造成立木间生长差异较大[20]。已有研究[18,19]表明即使在很小范围内,影响立木胸径生长的异质性仍然存在,这限制了模型预测精度及应用范围,而非线性混合效应模型通过随机效应参数能够有效解决此类问题[21]。从现有研究来看,胸径-年龄单木生长模型大都为线性模型或线性混合效应模型,而对不同发育阶段且包括主要立地因子的非线性混合效应模型研究还未见报道。因此,单木胸径生长模型还需深入研究。
本文以华北暖温带华北落叶松人工林为研究对象,首先确定影响立木胸径生长的主要因子;其次基于主要限制性因子,建立华北落叶松人工林不同龄组单木胸径生长的非线性混合效应模型,以提高胸径生长模型的预测精度及适用性。
1 研究区概况
研究区位于河北省最北部的塞罕坝机械林场,地理位置为116°41′13″~118°31′43″E,41°16′24″~42°52′18″N,为典型的山地地形,属寒温性大陆季风气候,海拔在1021 m~1880 m的范围内,平均坡度15°;年均气温为-1.2℃,极端最高气温为33.4℃,极端最低气温-43.3℃;年均降水量约45 2 mm,主要集中于7~8月,占年降水量的67.6%;土壤类型主要有灰色森林土、棕壤土、风沙土、沼泽土、砾石土、草甸土等。研究区主要乔木树种有华北落叶松(Larix principis-rupprechtii)、白桦(Betula platyphylla)、云杉(Picea asperata)、樟子松(Picea Mongolica)、山杨(Populus davidiana)、蒙古栎(Quercus mongolica)等;主要灌木树种有绣线菊(Spiraea salicifolia)、细叶小檗(Berberi s poiretii)、黄刺玫(Rosa xanthina)、库页悬钩子(Rubus sachalinensis)、红瑞木(Cornus alba)等;主要草本植物有蒲公英(Herba taraxaci)、并头黄芩(Scutellaria scordifolia)、苔草(Carex tr istachya)、桔梗(Platycodon grandiflorus)、地榆(Sanguisorba officinalis)、照山白(Rhododendron micranthum)等。
2 研究方法
2.1 数据来源
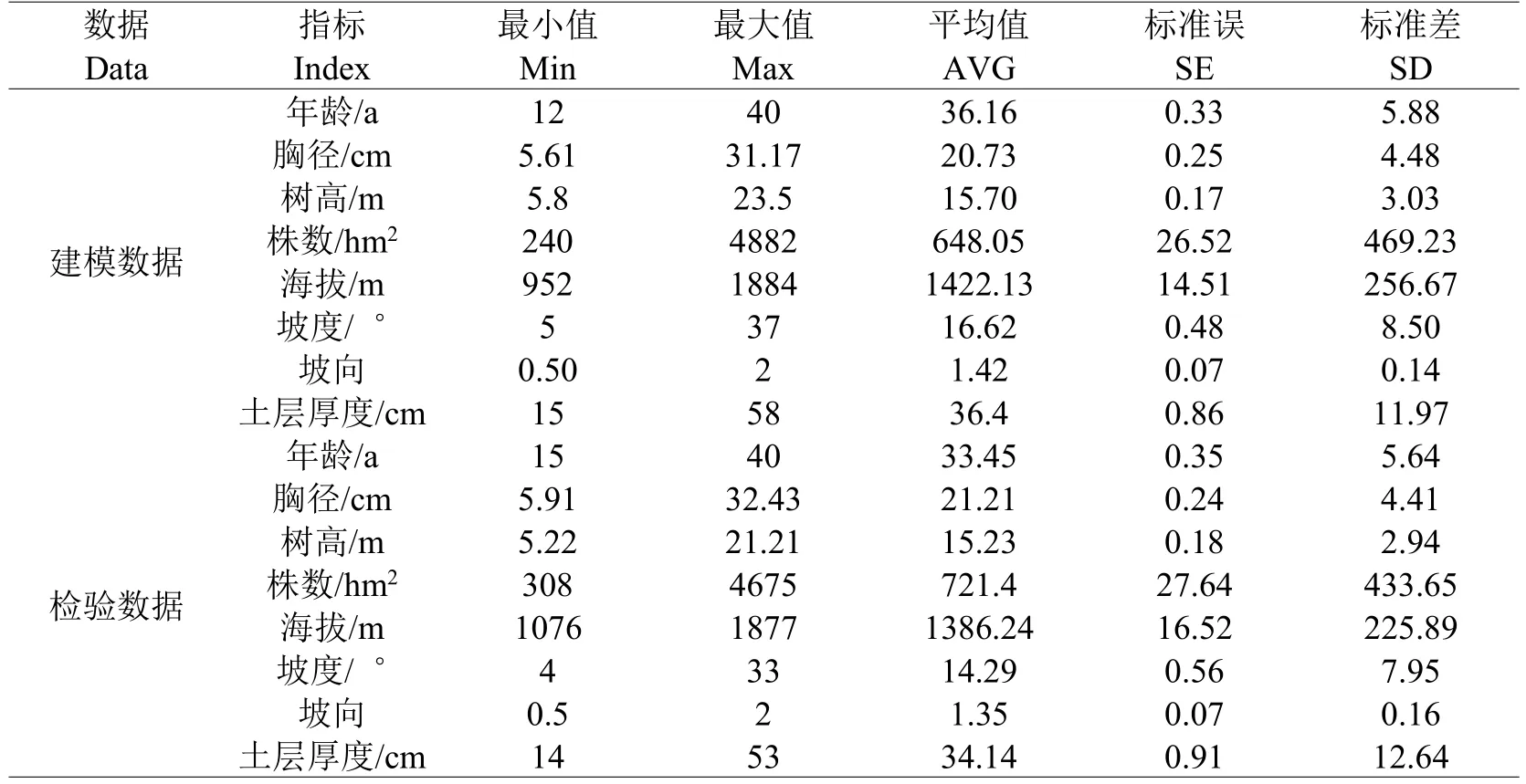
表1 建模数据和检验数据统计Table 1 Statistics for modeling and testing data
数据来源于2012年7~8月、2013年7~8月在塞罕坝机械林场下属的北曼店林场、千层板林场、大唤起林场、阴河林场,共设置不同龄组(11~20 a、21~30 a、31~40 a)华北落叶松人工林样地171块,其中临时样地(30 m×30 m)150块,固定样地(50 m×50 m)21块。观测并记录样地主要立地因子(海拔、坡度、坡向、坡位、土层厚度等),对所有样地内胸径大于5 cm的立木进行每木检尺,共观测立木20947株,在固定样地中以平面坐标形式记录立木在固定样地内的相对位置,此外在每块样地内选取2株优势木进行树干解析,解析木共342株,以确定立木年龄及年径向生长量。
2.2 基础模型选择
目前大部分学者使用[11-13]单木线性胸径生长模型来预测立木自然生长过程,Martin-Benito[2]认为线性生长模型限制了其应用范围及预测精度。近几年非线性建模方法引起了人们的关注[15,16],并采用非线性混合效应模型来解决样本误差[6,22,23]。当通过最佳线性无偏估计法来预测立木水平及样地水平的随机效应并进行校准后[8],混合效应模型可以提高模型预测精度[24]。在初步分析了几种线性模型[5]和非线性胸径-年龄生长模型(Chapman-Richards模型、分位数模型[6])的基础上,本研究确定使用Lee[25]等开发的非线性胸径-年龄生长模型作为构建混合效应模型的基础模型进行研究,其非线性胸径-年龄生长模型表达式为:

Δrtj为第j株树第t年生长量(cm),A立木年龄,D为胸径(cm),SQt为立地因子组合,CI为竞争指数,di参照树胸径(cm),dj竞争树胸径(cm),Distij参照树和竞争树距离(m)。
第n年胸径生长量(Dt+nj)可用包含当前观测胸径(Dtj)、年龄及竞争指数的函数进行计算,如公式所示:

2.3 模型检验
基于常见统计量对模型拟合精度进行评价:绝对误差(Bias)、均方根误差(RMSE)及确定系数(R2)对拟合模型进行评价与检验。

Dij为第i个样地第j株树的胸径观测值(cm);为第i个样地第j株树的胸径预测值(cm);为林分胸径(cm);n为观测样木株数;m为样地数;p为模型参数个数。
2.4 统计处理
采用SPSS21.0统计分析软件中的相关性分析,确定影响立木胸径生长主要因子及林分平均竞争指数(CI),模型建立采用ForStat2.1统计软件和SAS9.2软件中PROC NLMIXED完成。
3 研究结果
3.1 影响因子筛选
华北落叶松人工林近胸径平均年生长量与不同立地因子相关性分析如图1所示,其中每公顷株数、海拔、坡向、土层厚度是影响华北落叶松人工林胸径生长相关性较大,其相关系数分别为0.67、0.51、0.54、0.38。因此,确定每公顷株数、海拔、坡向、土层厚度是影响华北落叶松人工林胸径生长的主要因子。

图1 立地因子与胸径生长量相关性分析Fig.1Analysis on the correlation between annual radial growth and site factors
3.2 立木竞争
不同龄组华北落叶松人工林胸径分布格局如图2所示,幼龄林竞争指数为6.26,中龄林竞争指数为2.17,近熟林竞争指数为0.61。在人工林中由于受到经营水平及经营方式的影响,林分平均竞争指数随着林龄的增加而逐渐减小,林分竞争指数能够揭示密度对立木径向生长的影响。
3.3 混合效应模型构建

图2 华北落叶松不同发育阶段分布格局Fig.2 Distribution pattern of Larix principis-rupprechtii in different age groups
建立包含主要立地因子非线性混合效应模型来解决主要立地因子对立木径向生长量的影响,并将不同龄组林分竞争指数作为哑变量来解决不同龄组林分密度对立木胸径生长的影响,那么不同龄组华北落叶松人工林立木胸径生长模型可表示为:
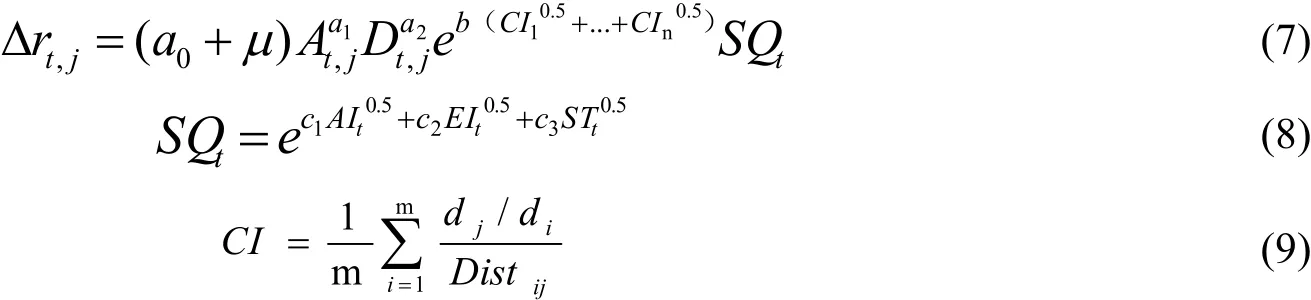
Δrt,j为第j株树第t年生长量(cm),a0、a1、a2、b、c1、c2、c3为固定效应参数,μ为样地随机效应参数,CI10.5…CIn0.5为人工林第n个龄组林分竞争指数哑变量;A为立木年龄(a),D为胸径(cm);CI为林分竞争指数,m为样地立木株数,di为参照树胸径(cm),dj为竞争树胸径(cm),Distij为参照树和竞争树距离(m);SQt为立地因子组合,EI为海拔(m)、AI为坡向、ST为土层厚度(cm)。
3.4 参数估计及检验
对不同龄组华北落叶松人工林胸径生长非线性混合效应模型进行了参数拟合,模型参数估计值、确定系数(R2)、绝对误差(Bias)及均方根误差(RMSE)如表2所示。不同龄组模型BIC值分别为-142.3、-109.4、-94.7;AIC值分别为:-145.8、-129.5、-113.6;-2 Log Likelihood值分别为:-463.8、-147.5、-131.6。运用拟合模型对不同龄组华北落叶松人工林胸径生长量进行了预测,不同龄组华北落叶松人工林径向生长量残差分布如图3所示。
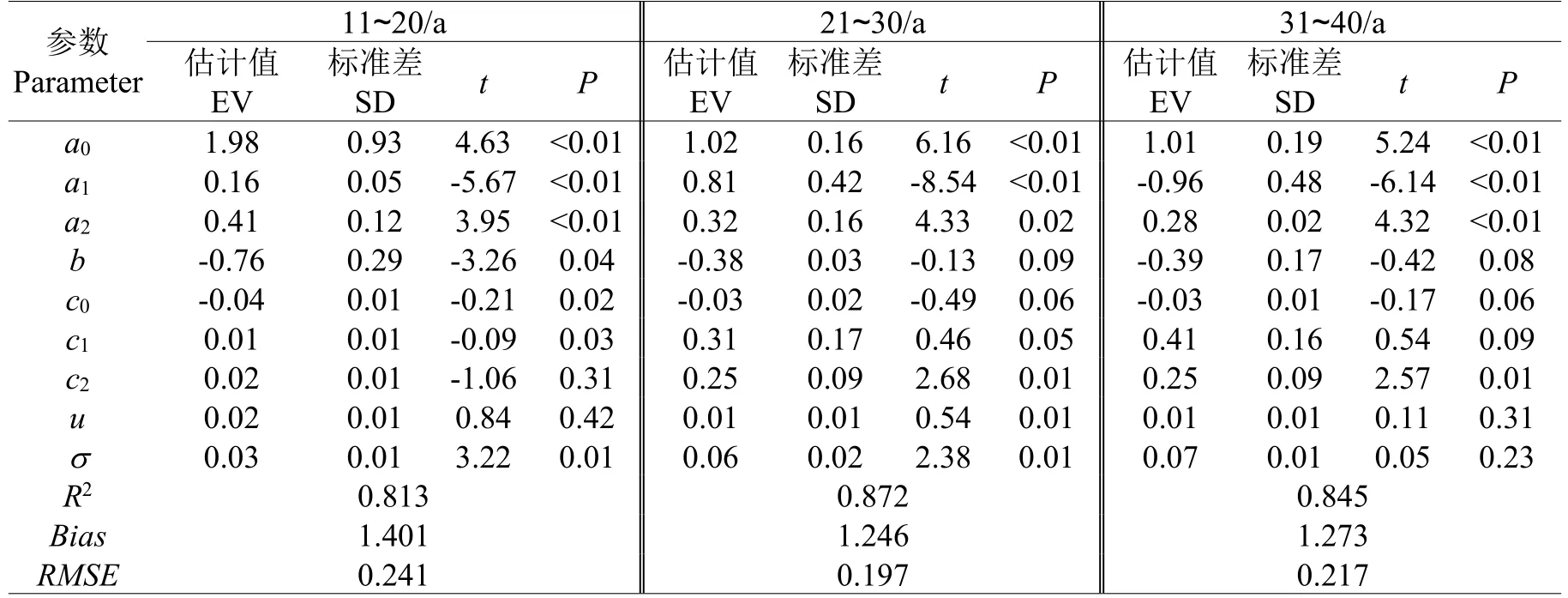
表2 不同龄组华北落叶松非线性混合模型参数估计及统计检验Table 2 Parameter estimations and statistics of nolinear mixed models of Larix principis-rupprechtii in different ages

图3 不同林龄胸径生长残差分布Fig.3 The residual distribution of DBH growth in different ages
4 讨论
立木胸径生长量预测模型通常为一个复合模型,会受到林分密度、年龄及立地因子等多种因素的影响[11,21]。本文以不同龄组华北落叶松人工林为研究对象,构建包含哑变量不同龄组单木胸径生长量的非线性混合效应生长模型。通过对所选择的6个因子与胸径生长量进行相关分析,确定密度、海拔、坡向、土层厚度与华北落叶松人工林立木胸径生长量相关性较强,这与Hannu[26]研究环境因子对美洲落叶松(Larix laricina)胸径生长量影响的结论一致。在人工林中立木胸径生长量受立木年龄和林分密度影响较大,随着年龄增加立木径向生长量逐渐降低,并呈现出倒J字形增长趋势,从模型拟合结果来看,当其它立地因子保持不变时,胸径生长量与参数a0和a1关系最为密切,其中a1在不同龄组对立木胸径生长影响不同,在幼龄林和中龄林阶段表现为正相关性,进入成熟林阶段后随着年龄的增加呈负相关性,这与Lhotka[27]和John[28]研究橡树(Quercus palustris)和短叶松(Pinus spp.)的结果一致。
不同发育阶段华北落叶松人工林胸径参数均为正值而竞争指数参数均为负值,在同龄林中立木胸径年生长量受立木竞争因素影响最大并与竞争指数呈负相关关系。在人工纯林中,Wykoff[29]认为立木对光照、水分和养分的竞争是对称的,胸径较大的立木对水分和养分竞争能力强[30],胸径生长量就大,反之竞争能力就弱,胸径生长量就相对较小。林分竞争指数揭示了立木竞争能力,而竞争对立木径向生长所产生的消极影响已经得到了许多研究的证实[30-31]。在华北落叶松人工林中竞争指数随着林龄的增加而减小,主要是受经营措施的影响,其中幼龄林仅抚育一次,而中龄林和近熟林已经过多次抚育,Guilley[32]也认为立木径向生长变异大都发生在林分水平上,造林初始密度及经营措施[8]对立木胸径生长产生影响较大。
立木胸径生长量是林分稳定性的重要指标,并受到多种立地因子影响[33],海拔、坡向及土层厚度是影响华北落叶松人工林径向生长量主要因子。海拔在不同发育阶段对径向生长量均表现为负相关性,在生长季内适宜的温度能够促进立木生长[34],北方山区低温限制了林木径向生长,在生长季内随着海拔的升高温度逐渐降低,生长季就会缩短,Ellenberg[35]研究表明海拔每升高100 m,生长季就缩短5~7 d,温度被普遍认为是影响立木胸径生长的主要限制因素[36,37],研究区海拔与不同龄组华北落叶松人工林径向生长量呈负相关关系。
在不同龄组土层厚度和坡向与立木径向生长量均表现为正相关性,水分对立木径向生长具有积极作用[38],阴坡土壤水分含量较高,土壤具有较好的保水能力。因此,阴坡立木胸径年生长量大于阳坡年生长量,这与彭剑峰等[39]研究坡向对祁连圆柏树(Sabina przewalskii)生长的结论相同。在生长季内土层越厚土壤水分含量相对较高,Linderholm[40]研究表明土壤含水量与土层越厚呈正相关关系,较低的土壤含水量限制了立木生长,土层越厚土壤保水能力越强,对立木胸径年生长量具有促进作用,并与La Pointe-Garant[41]研究苏格兰松(Scots pine)胸径生长量结论相同。
在同一样地的样本间具有空间相关性,立木胸径生长量残差并不是相互独立的[24],Palahi[42]认为可以用气候来解释。在生长季内叶面积及碳水化合物会对林木径向生长产生较大影响,而在本文研究中气候并不能解释模型所产生的所有变异,在Calama[30]研究结论中也获得了相同的结果,并表明混合效应模型中随机效应参数可以很好的解释这一结果。混合效应模型中固定效应参数能够反映大多数立木胸径生长量随年龄的变化总趋势,样地间随机效应参数能解释年龄和胸径生长曲线的变异,因此包含哑变量的混合效应模型提高了对不同龄组立木胸径生长量预测精度及适用范围。
[1]Leites LP,Robinson AP,Crookston NL.Accuracy and equivalence testing of crown ratio models and assessment of their impact on diameter growth and basal area increment predictions of two variants of the Forest Vegetation Simulator[J].Candian Journal of Forest Ressearch,2009(3):655-665
[2]Martin-Benito D,Kint V,Muys B,et al.Growth responses of West-Mediterranean Pinus nigra to climate change are modulated by competition and productivity:past trends and future perspective[J].Forest Ecology and Management, 2011(262):1030-1040
[3]Black BA,Abrams MD.Use of boundary-line growth patterns as a basis for dendroecological release criteria[J]. Ecological Applications,2003(13):1733-1749
[4]Bugmann H.A review of forest gap models[J].Clim Change,2001(51):259-305
[5]Hall DB,Clutter M.Multivariate multilevel nonlinear mixed effects models for timber yield predictions[J].Biometrics, 2004(60):16-24
[6]Fang Z,Bailey RL.Nonlinear mixed effects modeling for slash pine dominant height growth following intensive silvicultural treatments[J].Forest Science,2001(3):287-300
[7]Nothdurft A,Kublin E,Lappi J.A non-linear hierarchical mixed model to describe tree height growth[J].European Journal of Forest Research,2006(125):281-289
[8]Adame P,Hynynen J,Canellas I.Individual-tree diameter growth model for rebollo oak(Quercus pyrenaica Willd.) coppice[J].Forest Ecology and Management,2008(255):1011-1022
[9]Heiri C,Wolf A,Rohrer L,et al.Forty years of natural dynamics in Swiss beech forests:structure,composition,and the influence of former management[J].Ecological Applications,2009(19):1920-1934
[10]Cao QV.Incorporating whole-stand and individual-tree models in a standtable projection system[J].Forest Science, 2007(53):45-49
[11]Pokharel B,Froese RE.Representing site productivity in the basal area increment model for FVS-Ontario[J].Forest Ecology and Management,2009(258):657-666
[12]Zhang L,Peng C,Dang Q.Individual-tree basal area growth models for jack pine and black spruce in northern Ontario[J].Forestry Chronicle,2004(80):366-374
[13]Lacerte V,Larocque GR,Woods M,et al.Calibration of the forest vegetation simulator(FVS)model for the main forest species of Ontario[J].Candian Journal of Forest Ressearch,2006(199):336-349
[14]Calama R,Barbeito I,Pardos M,et al.Adapting a model for even-aged Pinus pinea L.stands to complex multi-aged structures[J].Forest Ecology and Management,2008(256):1390-1399
[15]Crecente-Campo F,Soares P,Tome M,et al.Modelling annual individual-tree growth and mortality of Scots pine with data obtained at irregular measurement intervals and containing missing observations[J].Forest Ecology and Management,2010(11):1965-1974
[16]Subedi N,Sharma M.Individual-tree diameter growth models for black spruce and jack pine plantations in northern Ontario[J].Forest Ecology and Management,2011(261):2140-2148
[17]Bohora SB,Cao QV.Prediction of tree diameter growth using quantile regression and mixed-effects models[J].ForestEcology and Management,2014(319):62-66
[18]Fajardo A,McIntire EJ.Distinguishing microsite and competition processes in tree growth dynamics:an a priori spatial modeling approach[J].American Naturalist,2007(169):647-661
[19]Fox JC,Bi H,Ades PK.Spatial dependence and individual-tree growth models.I.Characterising spatial dependence[J]. Forest Ecology and Management,2007(245):10-19
[20]Costa A,Pereira H,Oliveira A.Variability of radial growth in cork oak mature trees under cork production[J].Forest Ecology and Management,2003(175):239-246
[21]Weiskittel AR,Garber SM,Johnson GP,et al.Annualized diameter and height growth equations for Pacific Northwest plantation-grown Douglas-fir,estern hemlock,and red alder[J].Forest Ecology and Management,2007(250):266-278
[22]Trincado G,Burkhart HE.A generalized approach for modeling and localizing stem profile curves[J].Forest Science, 2006(52):670-682
[23]Sharma M,Parton J.Modeling stand density effects on taper for jack pine and black spruce plantations using dimensional analysis[J].Forest Science,2009(55):268-282
[24]Calama R,Montero G.Interregional nonlinear height–diameter model with random coefficients for stone pine in Spain[J].Candian Journal of Forest Ressearch,2004(34):150-163
[25]Lee WK,Gadow KV,Chung DJ.DBH growth model for Pinus densiflora and Quercus variabilis mixed forests in central Korea[J].Ecological Modelling,2004(176):187-200
[26]Hannu H,Hannu S,Erkki A.Effect of temperature and precipitation on the annual diameter growth of Scots pine on drained peatlands and adjacent mineral soil sites in Finland[J].Dendrochronologia,2012(30):157-165
[27]Lhotka JM,Loewenstein EF.An individual-tree diameter growth model for managed uneven-aged oak-shortleaf pine stands in the Ozark Highlands of Missouri,USA.[J].Forest Ecology and Management,2011(3):770-778
[28]John M,Edward F,Loewenstein.An individual-tree diameter growth model for managed uneven-aged oak-shortleaf pine stands in the Ozark Highlands of Missouri,USA[J].Forest Ecology and Management,2011(261):770-778
[29]Wykoff WR.A basal area increment model for individual conifers in the Northern Rocky Mountains[J].Forest Science, 1990(36):1077-1104
[30]Calama R,Montero G.Multilevel linear mixed model for tree diameter increment in stone pine(Tinus pinea L.):a calibrating approach[J].Silva Fennica,2005(39):37-54
[31]Monserud RA,Sterba H.A basal area increment model for individual trees growing in even-and uneven-aged forest stands in Austria[J].Forest Ecology and Management,1996(80):57-80
[32]Guilley E,Herve JC,Nepveu G.The influence of site quality,silviculture and region on wood density mixed model in Quercus petraea Liebl[J].Forest Ecology and Management,2004(189):111-121
[33]Sonja V,Robert A,Monserud HS.Do individual-tree growth models correctly represent height:diameter ratios of Norway spruce and Scots pine[J].Forest Ecology and Management,2010(260):1735-1753
[34]Bronson DR,Gower ST,Tanner M,et al.Effect of ecosystem warming on boreal black spruce bud burst and shoot growth[J].Global Change Biology,2009(15):1534-1543
[35]Ellenberg H,Leuschner C.Vegetation Mitteleuropas mit den Alpen:inökologischer,dynamischer und historischer Sicht[J].Journal of Ecology,1984,72(2):314-315
[36]Davi H,Dufrene E,Francois C,et al.Sensitivity of water andcarbon fluxes to climate changes from 1960 to 2100 in Europeanforest ecosystems[J].Agricultural and Forest Meteorology,2006(141):35-56
[37]Delpierre N,Dufrene E,Soudani K,et al.Modelling inter annual and spatial variability of leaf senescence for three deciduous species in France[J].Agricultural and Forest Meteorology,2009,149(5):938-948
[38]Zweifel R,Zimmermann L,Zeugin F,et al.Intra annual radial growth and water relations of trees:implications towards a growth mechanism[J].Journal of Experimental Botany,2006(57):1445-1459
[39]彭剑峰,勾晓华,陈发虎,等.坡向对海拔梯度上祁连圆柏树木生长的影响[J].植物生态学报,2010,34(5):517-525
[40]Linderholm HW,Solberg BQ,Lind holm M.Tree-ring records from central Fennoscandia:the relationship between tree growth and climate along a west east transect[J].Holocene,2003(13):887-895
[41]La Pointe-Garant MP,Huang JG,Gea-Izquierdo G.Use of tree rings to study the effect of climate change on trembilng aspen in Québec[J].Global Change Biology,2010(16):2039-2051
[42]Palahi M,Pukkala T,Miina J,et al.Individual tree-growth and mortality models for Scots pine(Pinus sylvestris L.)in North-East Spain[J].Annals of Forest Science,2003(60):1-10
The Diameter at Breast Height and Age Growth Model of Larix principis-rupprechtii Plantations with DifferentAge Groups
ZHANGDong-yan1,2,WANGDong-zhi2*,ZHANGZhi-dong2,HUANGXuan-rui2
1.College of Business/Hebei Agricultural University,Baoding 071000,China 2.College of Forestry/Hebei Agricultural University,Baoding 071000,China
This paper studied the Larix principis-rupprechtii plantations of different age groups and determined the nonlinear single tree diameter growth model as the basic model.Considering the influence of the main site factors and density on diameter growth of Larix principis-rupprechtii at different stages of development,a nonlinear mixed effects model of different age groups was established by using dummy variable method,including the competition index and main site factors of different age groups.The results showed the main limiting factors of the growth were density,elevation,slope and soil thickness by correlation analysis of site factors and tree DBH growth.The correlation coefficients were 0.67,0.51,0.54,0.38; The competition index of the forest was negatively correlated with the age groups due to the difference of operation and management level.The average competition index of the different age groups were 6.26,2.17,0.61;the nonlinear mixed effects model of different age groups including main site factors was established by dummy variables.The BIC value of different age group model were-142.3,-109.4,-94.7 for BIC;-145.8,-129.5,-113.6 for AIC;-463.8,-147.5,-131.6 for-2 Log Likelihood.Under different site conditions,fixed effects parameters can reflect most tree diameter growth with age change trend and the random effect parameters can explain the variation of the growth curve of different tree age.Therefore, the nonlinear mixed effects model improved the prediction accuracy and applicable range of diameter growth.
Larix principis-rupprechtii;plantation;site factors;nonlinear mixed-effects model;DBH
S758.5+7
:A
:1000-2324(2017)03-0449-07
2016-10-11
:2016-12-22
林业公益性行业科研专项(20150430304);国家自然科学基金(31370636);结构调控对人工林生产力形成的影响机制(2016YFD060020303)
张冬燕(1979-),女,在读博士,讲师.主要研究方向为森林可持续经营.E-mail:zhdys@163.com
*通讯作者:Author for correspondence.E-mail:wangdz@126.com
