基于支持向量机的交通标志人工智能检测与识别

何诚刚

西安交通大学城市学院,陕西 西安 710018

基于支持向量机的交通标志人工智能检测与识别

何诚刚

西安交通大学城市学院,陕西 西安 710018

针对人工智能检测与识别交通标志准确率不高的问题，本文提出了一种以支持向量机(SVM)为基础的多方法相融合的交通标志检测与识别方法。该方法首先采用方向梯度直方图进行交通标志的特征数据提取，然后利用网格搜索法和交叉验证方法对支持向量机模型最优化参数组合（惩罚因子C和核参数r）进行搜索，最后利用优化的支持向量机模型现实交通标志识别。实验仿真结果表明：基于支持向量机的最优化交通标志识别的准确率可达98%。

支持向量机;交通标志;智能检测;识别

目前伴随无人车以及辅助驾驶系统技术的快速发展，交通标志智能检测与识别已成为无人驾驶控制系统的重要组成部分，而目前由于道路交通的复杂性以及交通标志识别技术的研究尚不够完善，该问题已成为制约无人驾驶汽车发展的一个瓶颈[1,2]。因此针对交通标志人工智能检测与识别的研究具有重要的研究意义。目前国内外针对交通标志的识别主要研究包括SIRF、SURF算法以及神经网格、支持向量机和Adaboost等机器学习方法[3-6]。其中支持向量机具有快速建立识别模型以及更适合于小样本数据下的模型建立，因此本文采用支持向量机算法为基础相与方向梯度直方图（HOG）法、网格搜索法和交叉验证法相结合的方式进行交通标志人工智能检测与识别研究。

1 相关理论

支持向量机（Support Vector Machine,SVM）为近年来新兴起的一种优秀的人工智能识别方法，于1995年由贝尔实验室的Vapnik提出来的，该方法主要用来解决样本的分类和回归两大问题[7,8]。支持向量机方法理论是建立在基于统计学的VC维理论和结构风险最小化理论的基础上发展起来了，其能够结合样本信息进行学习精度以及无错误识别样本能力之间获得最佳折衷，从而获取最优的推广能力。

支持向量机算法是一种基于分类边界的方法，其基本原理可以通过二分类问题来进行描述，如图1所示。图中实心点和空心点分别代表了在高维空间中的两类样本数据，其中H代表了两类数据间的分类的超平面，而另外两个H1和H2则分别是过各类中离分类面最近的样本且平行于分类面的超平面，H1和H2之间的距离称之为分类间隔，图中落在H1和H2样本数据则被称为支持向量(Support Vectors)。假设线性可分样本集为(xi,yi),i=1,…,n,x∈Rd,y∈{+1,-1}是类别符号，在d维空间中线性判别函数的一般形式可以表示为：g(x)=w·x+b，分类间隔等于2/ǁwǁ，因此使间隔最大等价于使ǁwǁ最小。要求分类线对所有样本正确分类，就是要求它满足yi[(w·x)+b]-1≥0,i=1,2,…,n，上述问题可转换为约束优化问题，即求函数的最小值。根据拉格朗日函数可以定义如下：其中， ai＞ 0代表拉格朗日系数，解决最优化问题则可转变成计算w和b的拉格朗日函数极小值，根据Kuhn-Tucker条件，可将上述优化问题整理为：其中sgn(·)为符号函数。对于分析非线性划分问题可以通过采用非线性变换中 实现向高维空间H中线性的转换，即采用的形式。如果存在一个“核函数”K满足：原空间中的函数则可以用来进行变换空间中的点积，进而避免映射Φ的具体形式。按照泛函分析的理论，核函数只要能够满足Mercer条件，它即可与某一变换空间中的点积相对应，即存在映射成立。常见的满足Mercer条件的核函数有：

线性核函数： K（ x,y）=x· y；

支持向量机不仅能解决二分类问题，同时还可以采用“一对一”和“一对其余”方法来解决多分类问题，本文进行基于支持向量机的交通标志识别则应用了“一对一”的多分类问题解决方法，具体方法不再赘述。同时本文采用了台湾大学林智仁教授研究设计的SVM模式识别与回归的软件包（LIBSVM）进行模型的建立，LIBSVM是一个简单的，易于使用的并且快速有效的SVM分类器，同时还提供了相应的源代码，因此经常被用于模式识别方程中。

2 交通标志的人工智能检测与识别

2.1 数据选取和预处理

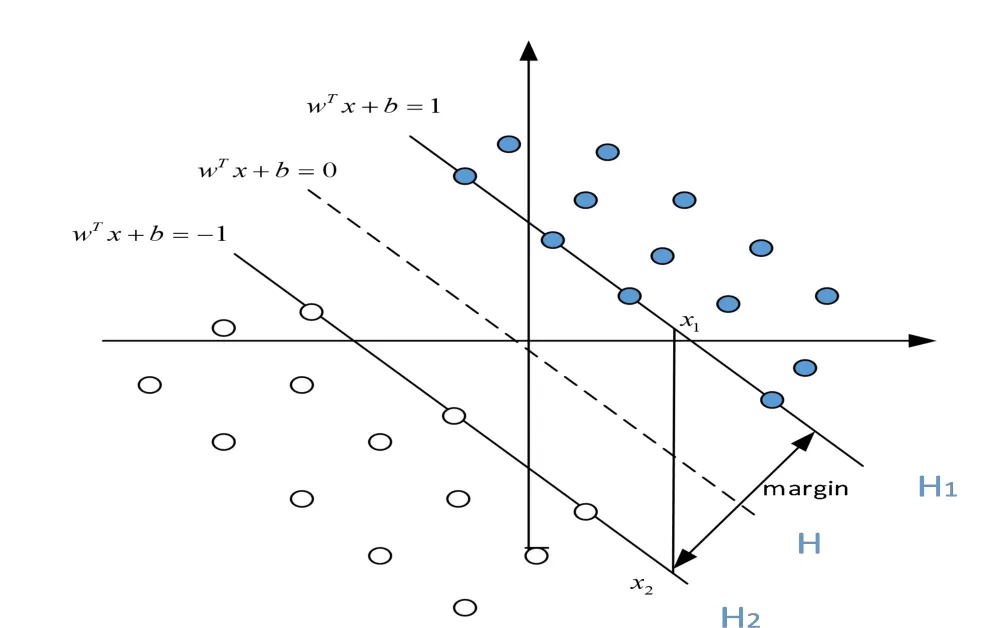
图1 线性二分类示意图Fig.1 Sketch of linear two classification

目前世界各国之间针对交通标志还没有形成国际性的规范，各国差异性较大，因此用于通用性研究的交通标志图像库并不多，而比较有代表性的图像库有GRSRB交通标志图像库、LinkopingUniversity交通标志图像库、ITOWNS交通标志图像库，其中GRSRB交通标志图像库具有较多的交通标志类别（如图2所示），且涵盖了多场景下交通标志。GRSRB交通标志图像库共涵盖了43种不同交通标志，总数超有50000张之多，本文选取了GRSRB标志库中6种共400张标志图片进行模型的训练和检测，其中选取300张标志用于模型的训练，另外100张照片用于模型的测试。对选取的400张交通标志图片需要进行特征提取，本文采用傅里叶描述子算法对交通标志进行处理获得含有交通标志的感兴趣区域（ROI），对于感兴趣区域进行域归一化处理为40×40大小格式图片，对处理后的图片采用方向梯度直方图（HOG）方法进行感兴趣区域的特征参数提取，此处采用HOG进行特征参数提取时，设定细胞单元cell像素大小为8×8，区域块block大小为16×16，每个block包含4个cell，区间bin为9，每个block的HOG特征为36维，对于本文中40×40的标志图片block步长为8，由此最终获得HOG描述子的特征共计576维（4×4×36）用于基于支持向量机的交通标志人工智能训练和识别。

图2 交通标志图集Fig.2 Traffic signs

2.2 人工智能识别流程

本文进行基于支持向量机的交通标志识别模型的建立流程如图3所示，具体流程如下：

(1)收集不同类别交通标志样本并进行特征数据提取；

(2)对原始样本特征数据分成训练集和测试集两部分；

(3)对影响支持向量机模型性能的核心参数（核函数、惩罚因子C、核参数r）采用交叉验证方法进行最优化计算；

(4)根据不同核函数下获取的最优化惩罚因子C和核参数r组合分别通过训练样本来建立交通标志智能识别模型；

(5)对建立好的交通标志识别模型采用测试样本进行测试，通过相关评价指标进行模型评价，评价指标包括准确率（Precision）、支持向量个数（N）和训练时间（T）三种，若评价结果满足要求则确定为最终交通标志识别模型，若不满足将返回第（3）级从新建立模型直至满足要求为止；

(6)待模型满足实际要求后则可对交通标志进行检测识别应用。

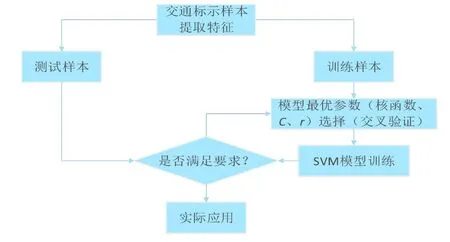
图3 交通标志识别模型建立流程Fig.3 The establishment process of traffic sign recognition model

2.3 识别结果

基于支持向量机建立的识别模型性能的优越性主要由核函数和惩罚因子C、核参数r来决定。本文采用的LIBSVM工具箱可提供常见的4种核函数，分别为线性核函数、多项式核函数、RBF核函数和Sigmoid核函数。实验中分别对每种核函数采用网格搜索和交叉验证相结合的方式进行处理。

网格搜索法是通过让惩罚因子C、核参数r分别在[2-10，2-9，…29，210]范围的网格节点上进行搜索，在每个节点将训练样本采用交叉验证方法进行验证，此处将训练样本分解成5组，每组又分解成两部分，一部分用于训练、另外一部分用于测试分类性能。交叉验证过程中每次从两组参数中任选一种用于测试，通过循环迭代方式对每种参数组合进行测试（总计15×15=255组参数值），每次迭代计算中会求取5组所对应的精度值，再求取这5组精度值的平均值作为本次迭代两组参数组合所对应的精度值，最后根据每次所计算的精度值进行模型惩罚因子C和核参数r组合策略评价。

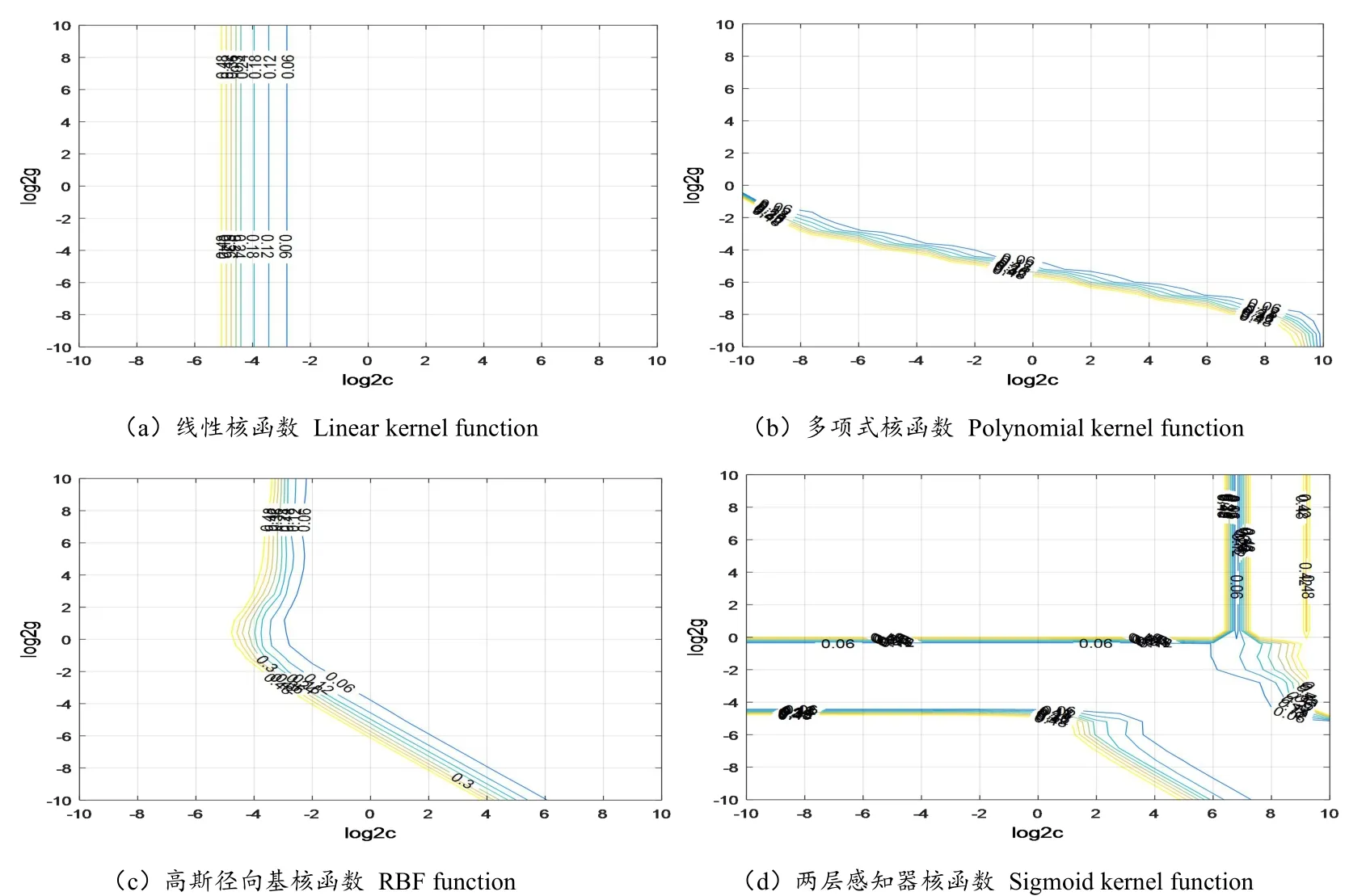
图4 不同核函数下交叉验证结果Fig.4 Cross validation results under different kernel functions

本文中对4种核函数分别应用交叉验证方法获得的惩罚因子C和核参数r最优化组合如图4所示，图中X轴为惩罚因子C取以2为底的对数后的数值，Y轴为核参数r取以2为底的对数后的数值，图中在同一颜色的线上为获得测试结果均方误差相同，对于多组惩罚因子C和核函数r对应同一均方误差，本文选取惩罚因子C最小的那组作为最佳模型构建参数，其原因为：惩罚因子C过高的话会降低模型的泛化能力，虽然训练集分类识别的准确率很高，但是测试集的分类识别的准确率却会很低。从图中可以看出针对不同核函数采用交叉验证方法获得惩罚因子C和核函数r组合各不相同，图（a）中采用线性核函数下获得的最优惩罚因子C=0.435，核参数r=0.001。图（b）中对于多项式核函数下获得的最优惩罚因子C=0.001，核参数r=6.964。图（c）中RBF核函数下获得的最优惩罚因子C=1.319，核函数r=0.250。图（d）Sigmoid核函数下获得的最优惩罚因子C=36.758，核参数r=0.0156。

3 讨论

本文分别针对4种最优参数组合进行了交通标志人工智能检测识别模型建立，对所建立的模型采用剩下的100组测试样本进行测试，测试结果采用准确率（Precision）、模型支持向量个数（N）和训练时间（T）进行评价，评价结果如表1所示。

表1 模型测试评价结果Table 1 Evaluation results of model test

从表1中可知，采用RBF核函数以及惩罚因子C=1.319和核参数r=0.250的组合下交通标志识别效果最好，其测试样本识别的准确率为98%，支持向量个数为65个，此处需要说明，支持量个数直接反应了模型的复杂化程度，模型建立过程的支持向量个数越多，其模型的训练时间长度越长，由于采用RBF核函数模型建立所需核函数较少，因此该模型建立所需时间则较短仅需9.97秒。采用多项式核函数所建立模型测试结果准确率为92%，再后为采用线性核函数，准确率为90%，最后为采用Sigmoid核函数测试结果准确率最低为89%。对比四种核函数获得不同测试结果的主要原因为RBF核函数可以很好的将一个样本映射到更高维数空间，同时对比多项式核函数，RBF需要确定的参数要少，降低了模型建立的复杂程度，Sigmoid函数部分功能与RBF核函数相似，但是其常用于神经网格的阈值函数，线性核函数主要用于线性可分的情形，核参数自身结构简单，运算速度快，但是对非线性问题适用性较差，因此采用RBF核函数更适合建立基于支持向量机的交通标志识别模型。表1中同样给出了采用支持向量机和BP神经网格两种方法测试的对比结果，通过对比可知采用BP神经网格建立交通标志识别模型测试结果的准确度仅为83%，同时训练时间确需要89.26 s，通过对比进一步证明了采用支持向量机更适合于交通标志的人工智能检测与识别。

4 结论

本文提取出的采用基于支持向量机方法进行交通标志的人工智能识别具有较高的准确度，同时本文中采用的网格搜索法和交叉验证相结合的方法可以更加有效的获得模型建立所需最优参数组合，通过实验研究表明：采用RBF核函数以及惩罚因子C=1.319和核参数r=0.250的最优组合所建立的交通标志识别的准确率可达到98%。综上所述，本文提出的基于支持向量机方法可为交通标志的人工智能检测和识别提供一种有效的技术方法。

[1]陈 龙,潘志敏,李清泉,等.利用ASIFT算法实现多视角静态交通标志识别[J].武汉大学学报:信息科学版,2013,38(5):553-556

[2]谷明琴,蔡自兴,李 仪,等.基于多模型表示的交通标志识别算法设计[J].控制与决策,2013,28(6):844-848

[3]杨 恒,刘肖琳.基于SURF的车载实时交通标志识别系统[J].微计算机信息,2011,27(6):101-102

[4]黄 琳,张尤赛.应用深层卷积神经网络的交通标志识别[J].现代电子技术,2015,38(13):101-106

[5]吴 峰,陈后金,姚 畅,等.基于网格搜索的PCA-SVM道路交通标志识别[J].铁道学报,2014(11):60-64

[6]王改革,郭立红,段 红,等.基于Elman_AdaBoost强预测器的目标威胁评估模型及算法[J].电子学报,2012,40(5):901-906

[7]Cortes C,Vapnik V.Support-vector networks[J].Machine learning,1995,20(3):273-297

[8]Vapnik VN,Vapnik V.Statistical learning theory[M].New York:Wiley,1998

The Intelligent Detection and Recognition for Traffic Signs Based on Support Vector Machine

HE Cheng-gang
Xi’an Jiaotong University City College,Xi’an 710018,China

To solve the problem of low accuracy of intelligent detection and recognition for traffic signs,a fused multi-phase method based on support vector machine theory was put forward for traffic signs detection and identification.Firstly,the histogram of oriented gradient(HOG)was used to extract the feature data of traffic signs.Then the grid search method and cross validation method were applied to search the optimal parameters combination(penalty factor C and kernel parameter r) of the support vector machine model.Finally,the optimal method of support vector machine was applied to identify the traffic signs.Experimental results indicated that the proposed method went up to accuracy 98%of the recognition for traffic signs.

Support vector machine;traffic signs;intelligent detection;recognition

TP39

:A

:1000-2324(2017)03-0400-05

2016-02-15

:2016-03-16

何诚刚(1968-),男,硕士,副教授.主要研究方向为通信工程及电子测量仪器.E-mail:cghe68@126.com