Eigen模型中误差阈展宽机制的研究

田中修，李多芳，曹天光，耿金鹏，展永

（河北工业大学理学院，天津300401）

Eigen模型中误差阈展宽机制的研究

田中修，李多芳，曹天光，耿金鹏，展永

（河北工业大学理学院，天津300401）

物种演化本质上是生物群体与他们周围环境之间相互作用的一个随机过程.即演化模型中的一些物理参量是受外界环境涨落的影响.本工作中，是把模型中的适应度和突变率这2个物理参量同时处理为高斯分布随机变量，当二者同步耦合随机化时，转变区域的宽度与适应度和突变率的涨落强度分别呈线性和指数型关系；二者在非同步耦合随机化的情况下，转变区域的宽度与变量涨落强度间的关系与之前相一致.此时，不同的涨落强度下，变量与转变区域的宽度呈现出不同的趋势.当适应度和突变率二者同时随机化时，突变率随机化占据了主导地位，这就需要将突变概率矩阵中矩阵元作进一步的分析，进而研究误差阈的展宽机制.

突变率；高斯分布随机变量；耦合随机化；突变概率矩阵；误差阈

0 引言

达尔文进化论，提出了选择和突变是生物演化的2个主要驱动力，对生物学产生了深远的影响.1971年，Eigen等人把选择和突变这2个参量引入到无生命的化学反应体系中，从而建立了物种演化的数学模型，即Eigen模型[1].Eigen模型预言了2个重要的结果：准物种和误差阈[2-3].突变序列围绕主系列形成的一种分布称之为准物种.而误差阈是一阈值，当突变率越过此阈值后，生物大分子将不再携带遗传信息且各序列将随机地分布在序列空间中.

自然界中的物种演化总是受到各种随机因素的影响，其中包括基因突变与外部的环境涨落[4-5].也就是说，物种演化模型中的物理参量是受这些随机因素支配的.即这些物理参量是随机性的而非是确定性的，应当被处理成随机变量.在之前的研究工作中，本课题组把Eigen模型中的适应度和突变率这2个变量分别处理成高斯分布随机变量[6-7].而本研究工作中，是把模型中的适应度和突变率这2个变量同时处理成高斯分布随机变量，进而研究误差阈的展宽现象.

当适应度和突变率这2个物理参量同时进行随机化时，突变率的随机化占主导地位[8].本文试图从根源出发，探讨突变率是如何影响生物的进化过程，这就需要对突变概率矩阵中矩阵元作进一步的讨论，进而研究误差阈展宽的机制.

1 模型

Eigen模型描述的是自复制分子的进化过程，不同的生物大分子携带着特定的遗传信息.这些生物大分子，例如，具有固定长度为N的序列.在DNA分子或RNA分子中，如果仅考虑嘌呤和嘧啶，生物分子的每一位点都是一个二进制变量，序列的总数为2N.为了简化模型，引入汉明距离将序列进行分类.将任意2条序列之间碱基数目的差异定义为汉明距离.与主序列相比，具有相同汉明距离的序列被归为一类，最终得到N+1类序列.Eigen模型演化的动力学方程：

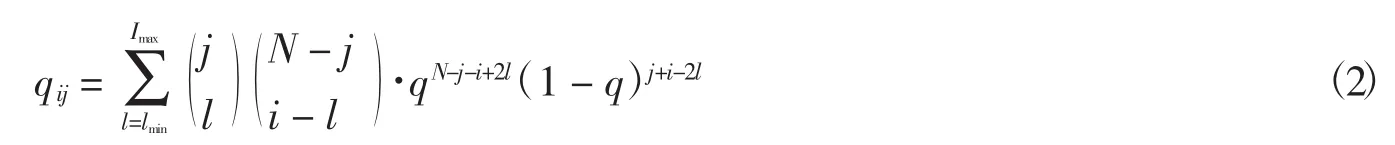
q代表序列每一位点的复制精度.假定只发生点突变，每一位点的突变率相同且相互独立，突变率表示为

为了研究Eigen模型的随机特性，需要把适应度和突变率同时处理为高斯分布随机变量.变量满足概率密度分布函数：

2 非同步耦合随机化的研究

由误差阈展宽与随机变量涨落强度之间的关系，可以定量的定义完全随机化模型中误差阈的范围.误差阈范围的起点为确定性模型中的临界点（相变点）.误差阈范围的终点为2个互补序列间相对浓度的相对差异小于0.01时的位点[11].相对差异c为：

根据误差阈的起点和终点，给出了随机变量在不同涨落强度下转变区域的范围和宽度.

图1直观的给出了适应度的涨落强度和突变率的涨落强度与误差阈宽度的关系.从图1a）可以看出，当突变率涨落强度为零（适应度单独随机化）时，误差阈宽度与适应度的涨落强度呈线性关系.而当突变率涨落强度不再为零（完全随机化）时，误差阈宽度与适应度的涨落强度也呈线性关系且斜率逐渐变小.由图1b）可知，当适应度涨落强度为零（突变率单独随机化）时，误差阈宽度与突变率的涨落强度近似呈指数型关系.同样的，而当适应度涨落强度不再为零（完全随机化）时，误差阈宽度与适应度的涨落强度也近似呈指数型关系且斜率也是逐渐变小.

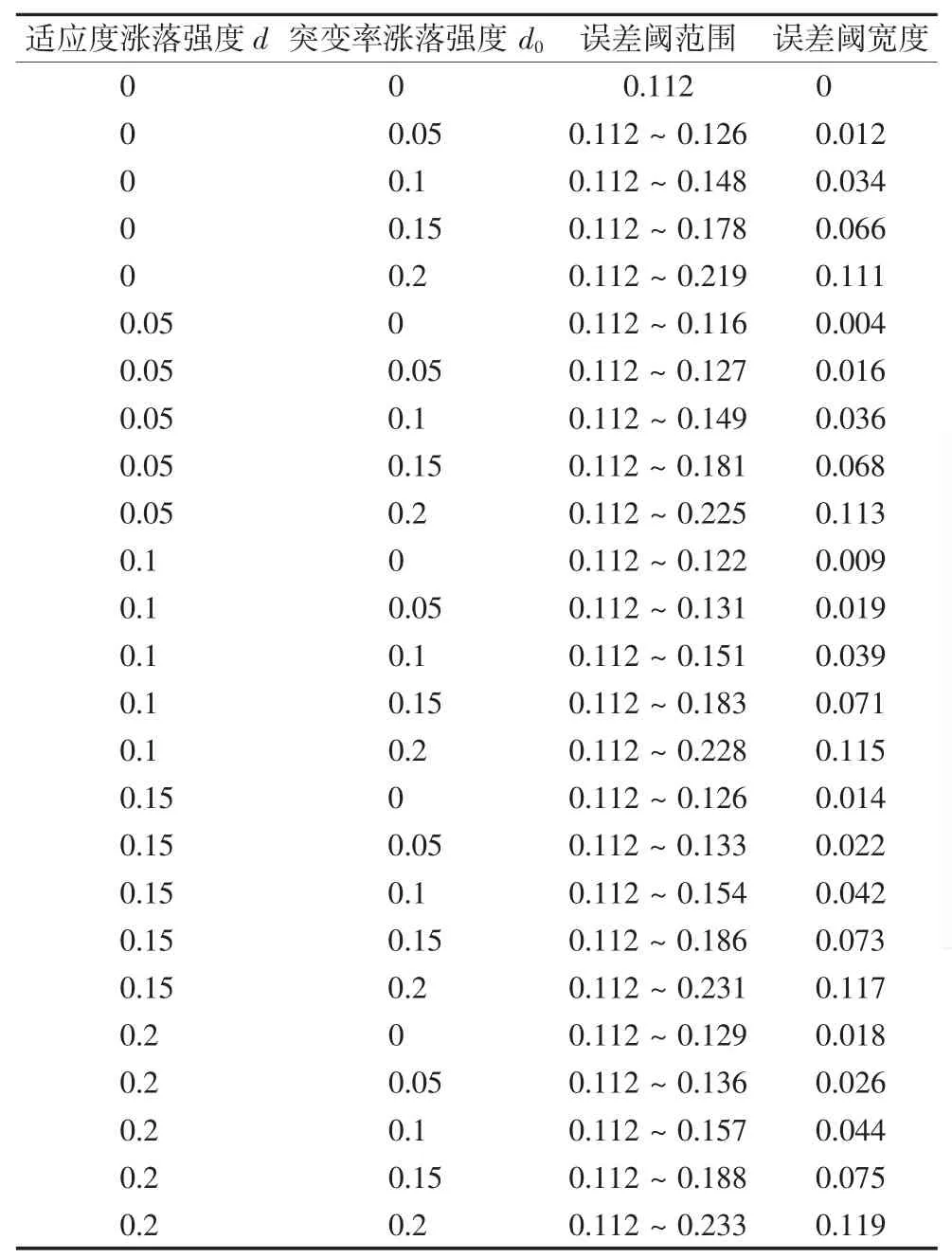
表1 适应度和突变率在不同涨落强度下，误差阈的范围和宽度Tab.1 The range and width of the error thresholds at different fluctuation strength of fitness and mutation rate

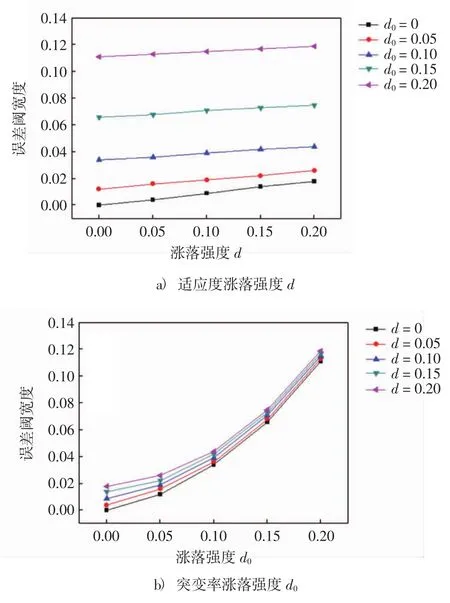
图1 适应度涨落强度d和突变率涨落强度d0取不同值时所对应的误差阈宽度Fig.1 The fitness fluctuation strength dand mutation rate fluctuation strength d0at different values corresponding to the error threshold width

3 突变概率矩阵的研究

当适应度和突变率同时随机化时，突变率随机化占主导地位.而突变率随机化之后最直观的体现应该是突变矩阵中矩阵元的变化.本文试图从突变矩阵出发，探讨突变率是如何影响生物进化过程的.引入汉明距离后将序列进行分类，可以得到n+1阶矩阵.突变概率矩阵Q的形式为：

在误差阈附近，得到了突变概率矩阵元素随突变率的变化，如图2所示.图2a）表示的是在确定性模型中突变概率矩阵随位点突变率的演化情况.从图中可以看出，突变概率矩阵中对角线附近的突变概率分布随突变率的增加而发生一定的旋转，旋转中心为矩阵的中心元素.同时，突变概率分布的峰脊形状发生改变.而在随机化后的模型中，如图2b）所示，出现相似突变概率分布时的突变率与确定性模型相比发生了滞后.同时，在随机化模型中，突变概率矩阵元素的峰值出现了边缘效应，即与确定性模型相比，矩阵元素的峰脊呈现出中间高两边低的特征.突变概率矩阵的特性决定了序列群体相对浓度的稳态分布，因此，突变概率分布的特征可能是稳态时分子物种的误差阈发生展宽的主要原因.

图2 在误差阈附近，确定突变概率矩阵与随机突变概率矩阵的对比Fig.2 In the vicinity of the error threshold，a comparison is made between the determine mutation probability matrix and the random mutation probability matrix

4 结论

误差阈是分子物种从生存到死亡的临界突变率，其对原始物种保护和病毒的灭亡尤其是对抗病毒策略的设计都具有重要的意义[12-13].随着病毒抗药性的不断增强，传统的消灭病毒的方法存在诸多的困难.准物种概念给出了两种病毒灭亡的方式：致死突变和越过误差阈.而通过增加病毒的突变率使其越过自身误差阈而消灭病毒的方法已在相关的病毒实验中得到了证实[14-15].

对于实际生物演化过程来说，对理论模型进行随机化讨论是必要的.在Eigen模型中，当适应度和突变率这两个物理量随机化之后误差阈的宽度与二者的涨落强度分别呈线性和指数型关系.而二者在非同步耦合随机化的情况下，曲线的斜率随着涨落强度的增大而逐渐减小.在突变概率矩阵中，随机化模型中的矩阵元在误差阈附近的演化滞后于确定性模型，且矩阵元素的峰值还出现了边缘效应.因此，本文从序列位点突变率随机化的角度阐述了在随机涨落情况下群体误差阈拓宽的机理，为准物种理论走向实际应用提供一定的理论参考和借鉴.

致谢：感谢中国原子能科学研究院顾建中研究员对本工作的指导和讨论.

[1]Eigen M.Selforganization of matter and the evolution of biological macromolecules[J].Die Naturwissenschaften，1971，58（10）：465-523.

[2]Eigen M，McCaskill J，Schuster P.Molecular quasi-species[J].The Journal of Physical Chemistry，1988，92（24）：6881-6891.

[3]Eigen M，McCaskill J，Schuster P.The Molecular quasi-species[J].Adv Chem Phys，1989，75：149-263.

[4]Nowak M，Schuster P.Error thresholds of replication in finite populations mutation frequencies and the onset of Muller′s ratchet[J].Journal of theoretical Biology，1989，137（4）：375-395.

[5]Campos P，Fontanari J.Finite-size scaling of the error threshold transition in finite populations[J].Journal of physics A：Mathematical and general，1999，32（1）：L1.

[6]Feng X.Error thresholds for quasispecies on single peak gaussian-distributed fitness landscapes[J].Journal of theoretical biology，2007，246（1）：28-32.

[7]Qiao Lihua，Zhao Tongjun，Gu Jianzhong，et al.Eigen model of randomness in species evolution[J].Acta Phys Sin，2014，63（10）：108701.

[8]LI Duofang，CAO Tianguang，GENG Jinpeng，et al.Error threshold of fully random Eigen model[J].Chinese Physics Letters，2015，32（1）：018702.

[9]Saakian D，Hu C K.Eigen model as a quantum spin chain：exact dynamics[J].Physical Review E，2004，69（2）：021913.

[10]FENG Xiaoli，GU Jianzhong，LI Yuxiao，et al.Error thresholds in single-peak gaussian distributed fitness landscapes[J].Communications in Theoretical Physics，2007，48（4）：763-768.

[11]Li Duofang，CAO Tianguang，GENG Jinpeng，et al.Statistical properties and error threshold of quasispecies on single-peak gaussian-distributed fitness landscapes[J].Journal of theoretical biology，2015，380：53-59.

[12]Eigen M.Error catastrophe and antiviral strategy[J].Proceedings of the National Academy of Sciences，2002，99（21）：13374-13376.

[13]Manrubia S C，Domingo E，Lázaro E.Pathways to extinction：beyond the error threshold[J].Philosophical Transactions of the Royal Society B：Biological Sciences，2010，365（1548）：1943-1952.

[14]Codoñer Francisco M，Darós José-Antonio，Solé Ricard V，et al.The Fittest Versus the Flattest：Experimental confirmation of the quasispecies effect withsubviralpathogens[J].PLoSPathog，2006，2（12）：1187-1193.

[15]Rajamani S，Ichida J K，Antal T，et al，Effect of stalling after mismatches on the error catastrophe in nonenzymatic nucleic acid replication[J]. Journal of the American Chemical Society，2010，132（16）：5880-5885.

[责任编辑 杨屹]

The extension mechanism of the error threshold in Eigen model

TIAN Zhongxiu,LI Duofang,CAO Tianguang,GENG Jinpeng,ZHAN Yong
（School of Sciences,Hebei University of Technology,Tianjin 300401,China）

Species evolution is essentially a random process of interaction between biological populations and their environments.As a result,some physical parameters in evolution modles are subject to statistical fluctuations.In this work,two important parameters in the Eigen model.The fitness and mutation rate are treated as Gaussian distributed random variables simultaneously.When the two are coupled by randomization,the width of the crossover region is linearly and exponentially related to the fluctuation of the fitness and the mutation rate.In the case of the random coupling,the relationship between the width of the crossover region and the fluctuating strength of the variable is consistent with the previous one.At the same time,the variable and the width of the crossover region show different trends under different fluctuation strengths. When both fitness and mutation rate are randomized,the randomization of mutation rate dominates,which requires further analysis of the matrix elements in the mutation probability matrix,and then studies the extension mechanism of the error threshold.

mutation rate;Gaussian distributed random variable;coupled randomization;mutation probability matrix;error threshold

Q61

A

1007-2373（2017）02-0032-05

10.14081/j.cnki.hgdxb.2017.02.006

2016-11-25

河北省自然科学基金（C2013202192）

田中修（1990-），男，硕士研究生．通讯作者：展永（1954-），男，教授，博士生导师．