LES－PBM模拟后台阶流动中颗粒的团聚

卢明涛，陈占秀，杨历，李阳

（河北工业大学能源与环境工程学院，天津300401）

LES－PBM模拟后台阶流动中颗粒的团聚

卢明涛，陈占秀，杨历，李阳

（河北工业大学能源与环境工程学院，天津300401）

采用大涡模拟（Large Eddy Simulation，LES）耦合颗粒群平衡模型（Population Balance Model，PBM）的方法进行了对气固两相流在后台阶突扩模型的模拟计算，流场的涡结构演化与实验结果吻合较好.在此计算结果的基础上，研究不同位置处、不同Stokes数下，以及不同体积分数（Vc）等条件下涡结构的变化对颗粒扩散和颗粒团聚效果的影响，结果表明涡结构的变化对颗粒的团聚有较大影响.颗粒的Stokes数较小，颗粒对涡结构的跟随性较强，但也对涡结构产生了破坏作用，使得流场开始部分颗粒的团聚效果较好，之后的破坏作用又逐渐地削弱了颗粒间的团聚.颗粒的体积分数越大对涡结构的破坏越强，导致颗粒的团聚逐渐减弱.

大涡模拟；颗粒群平衡模型；后台阶；颗粒团聚；涡结构

0 引言

PM2.5比表面积大、易于富集重金属等有毒物质，最近几年出现的雾霾天气也是由这种细颗粒物引起的，成为空气的首要污染物.而一般传统除尘设备很难将其脱除，超细颗粒物的团聚及脱除的研究已经成为一个重要的领域[1～3].许多专家学者从超细颗粒物的形成、颗粒的聚并机理以及聚并装置等多方面进行了研究.颜金培[4]等通过实验的方式研究了汽锅烟气中超细颗粒的聚并过程和聚并效率.赵海波[5]用PBM模型的团聚核、破碎核等模型和蒙特卡罗模型的数值计算方法研究了颗粒运动过程中的碰撞、团聚和破碎等事件，得到了颗粒尺寸分布的变化过程.Mao[6]等对循环流化床进行了研究，通过数值计算方法对颗粒团聚的过程进行了分析，得出超细颗粒团聚过程主要受湍流聚并过程的影响.Alipchekov[7]等对气溶胶超细颗粒的聚并效果进行了研究，通过数值模拟计算发现湍流流动现象中，颗粒的聚并过程受颗粒在流场中的运动的影响. Eibeck等[8]采用直接模拟蒙特卡罗方法包括PBE的解决方案使用随机粒子代表单个物理粒子.Yeoha and Tub[9]，Miller and Garrick[10]采用欧拉方法和PBE的离散化方法解决流体耦合问题.其中PBM模型是研究气固两相流中颗粒团聚、破碎、成核、长大的有效方法.Rigopoulos[11]在离散化模型中描述了颗粒尺寸分布，把颗粒粒径分为若干段，采用‘bins’的数目描述颗粒直径的分布.目前对颗粒团聚的研究成果主要集中在实验研究，细颗粒物团聚过程的数值模拟研究还需要深入探索中.

气固两相流中存在着一定固含率的固体颗粒，气相与固相之间存在着耦合和调制作用，运动非常复杂.后台阶流动是具有分离特性的特征流动，许多学者对其研究取得了优秀的成果.目前研究的方法主要采用大涡模拟（LES）和离散颗粒模型（Discrete Particle Model，DPM），DPM模型可以较多的追踪颗粒的运动轨迹，但颗粒的浓度一般小于10-6.王兵[12]采取LES和DPM离散颗粒模型相耦合的办法，对二维后台阶流动中颗粒的扩散采取了数值计算分析，得出在流场中不同St数的颗粒的扩散情况和颗粒对瞬时大涡的调制作用，表明颗粒尺度的变化影响大尺度涡对颗粒扩散的作用.Hogan等[13]和Wood等[14]发现颗粒的优先聚集的效应与颗粒St数联系紧密.Elghobashi[15]研究了不同颗粒的固含率、不同颗粒的尺度与气相湍流流场的联系，得出了在不同固含率范围内，颗粒对流场的影响.

为了分析涡结构与颗粒团聚之间的关系，本文采用LES和PBM的耦合模型模拟分析涡结构的演化过程，不忽略颗粒对流场的作用，考虑颗粒的粒径和体积分数等因素的影响，利用团聚核函数研究不同位置处、不同St数以及不同体积分数条件下涡结构的变化对颗粒团聚效果的影响.

1 模拟方法和基本方程

1.1 气相控制方程

采用LES方法对连续相（即气相）流体进行数值计算模拟，对与滤波宽度相比较大的涡的运动采取直接数值计算模拟，而对与滤波宽度相比较小的涡运动采取亚格子模型进行数值计算，LES方法的控制方程如下：

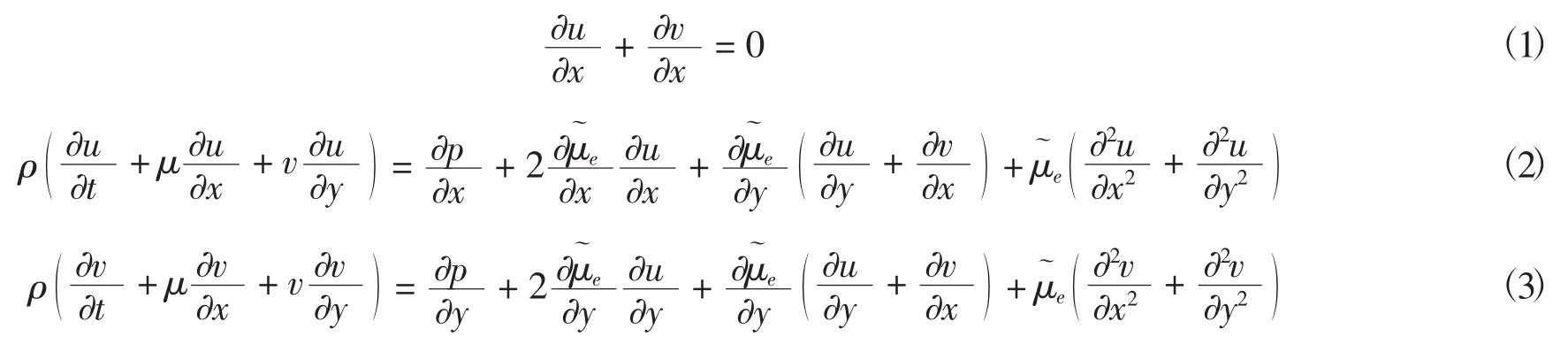
1.2 颗粒相方程

大气中含尘颗粒的粒径主要集中在0.04～0.3 μm内，98%以上颗粒的颗粒直径小于0.6 μm，本文仅考虑颗粒碰撞后的团聚过程，忽略颗粒碰撞后的破碎.PBM模型选用Discrete Model进行计算，其中的团聚模型时PBE方程如式（4）所示.

其中：N代表颗粒物浓度；β代表团聚核.选用的细颗粒物St≤1，属于有限惯性颗粒，并且由于颗粒被卷吸进入涡核中心才能进行团聚，与流场的雷诺数关系不大，所以采用自由分子团聚核函数进行模拟，如公式（5）所示，

St计算式如式（6）

2 边界条件和模型验证

2.1 物理模型和边界条件

为了与文献[16]的实验结果进行对照，计算中流动的几何参数与该实验工况完全一致，如图1结构尺寸：模型尺寸h=40 mm，H=26.7 mm，气相场采用充分发展槽道流动，主流速度u0=10.5 m/s.计算域取35H×2.498H，计算无量纲时间步长取10-3s，用Nt表示无量纲时间，x/H与Y/H为无量纲距离.

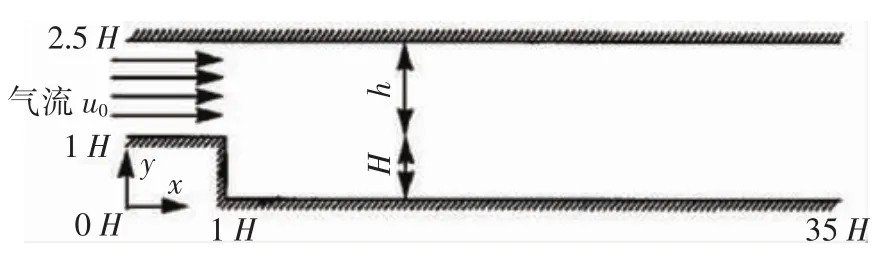
图1 后台阶流动示意Fig.1 Backward-facing step flow

气相流场的Re数定义与实验中的定义保持一致[16]，槽道进口的宽度作为长度尺度，槽道进口的速度作为速度尺度，即：

式中：H是台阶的高度；u0是入口的主流速度；按照此定义，实验验证时取ReH=18 400.

模拟过程中，初始入口压力场设置为零场，进口条件基于文献[16]中实验数据.

2.2 实验验证

图2呈现了在雷诺数为18 400时的情况下气固两相流后台阶流场中的涡结构的变化.图2中Nt=10所示，在流动初始阶段，在台阶后方首先发生涡的脱离，产生一次回流区，并随着流动的发展，如Nt=20所示，流体再附着于下壁面x/H=7.5位置处；随着流动进一步的发展，在接近顶部的壁面位置处产生二次回流漩涡区，对应Nt=40的情况，流场的再附着区在对应x/H=7.5的下壁面处，与Fessler等[17]的研究结果Xr/H=7.4位置相一致；流场继续发展时，在x/H=10位置靠近底部的下壁面附近开始出现三次回流漩涡区，对应图2中Nt=60的情况；随着流场的继续发展，涡线扭曲更加严重，槽道中的回流区和主流体呈现动态变化的状态，流场处于不稳定的状态，流动渐渐向过渡流和湍流方向发展.对不同特征截面的速度进行时均采样，得出瞬时场在Nt近似大于160时，流场达到动态稳定.依据文献[16]中的采样方式对Nt=160时瞬时速度场进行时间平均，得到速度时均值，见图3，从整体情况上模拟值与实验值吻合较好.文中后面的数值计算中采用的雷诺数也在18 400的条件下进行.

图2 瞬时流场涡结构的演变Fig.2 The evolution of the instantaneous flow field in vortex structure

3 计算结果与分析

3.1 不同位置处涡结构与团聚效果的联系

在Re=18 400、St=0.001条件下，分别研究x/H =3和15两个位置处涡结构对颗粒团聚效果的影响.x/ H=3处于台阶后的角涡回流区，x/H=15处于槽道中流场发展后的位置.

对于涉及气固两相流的后台阶流动，颗粒相的状态是颗粒扩散运动与气相大涡结构耦合作用的结果. Fessler[17]发现细颗粒物大多在涡量低、应变程度高的位置处发生聚集，而且会逃逸出涡量高的区域，涡量低和应变程度高的区域给颗粒的团聚过程提供条件.结合图2、3可知，x/H=3处于台阶后方的一次回流区（角涡回流区），存在速度和湍动能较小的涡结构，文献[18]证实了这一点.对于St＜＜O（1）和St～O（1）的颗粒粒径较小，颗粒扩散能力强，回流区中有大量的粒子存在[19]，颗粒进入涡量的角涡区局部聚集.研究的颗粒（St=0.001＜＜O（1），颗粒扩散能力强，在角涡区颗粒发生局部聚集增加颗粒浓度，高浓度下颗粒碰撞机率增加，从而有效增加颗粒团聚机会.团聚后颗粒粒径依然很小，不会逃逸出角涡区；由图2可知，随时间的增大角涡回流区变化并不明显，由于角涡区一直处于低涡量区，团聚后的颗粒不会随流场流入下游，角涡区成为颗粒团聚后的停滞区，颗粒在角涡区内停留或沉降.

图3 时均速度对比Fig.3 The contrast of temporal average velocity

图4中，Y/H=0～1之间时，处于台阶后的角涡回流区阶段，随无量纲时间的增大，角涡区的颗粒粒径增大；而Y/H=1～2.2属于主流体区域，区域内流体速度相对均匀，颗粒碰撞机会少停留时间短，颗粒粒径没有变化.综上所述，颗粒的团聚和粒径分布与涡结构联系紧密.

图4 x/H=3截面上粒径随时间的变化Fig.4 Particle size change over time（x/H=3）

图5表明，在x/H=15的截面上呈现不规律的团聚效果，波谷代表主流体区域颗粒粒径分布，波峰区代表大涡结构中的颗粒粒径分布.如在图5中Y/H= 0.5的位置处，随时间的变化，粒径呈现先增大后减小再增大的复杂趋势，在其他位置处也呈现复杂变化趋势.结合图2分析图5得出，随时间变化，进入涡结构的颗粒发生团聚，如在Nt=80～320时，Y/H= 0.5位置处的颗粒粒径随时间增大而增大；但由于流场的变化，主流体区域和涡结构的位置不断变化，产生涡结构的破碎与合并，旧的涡结构随流场流入下游，Y/H=0.5处产生新的涡结构分布，主流体与涡结构的位置发生变化，颗粒团聚后随主流区流入下游区域.流场中涡结构的破碎与合并改变了涡

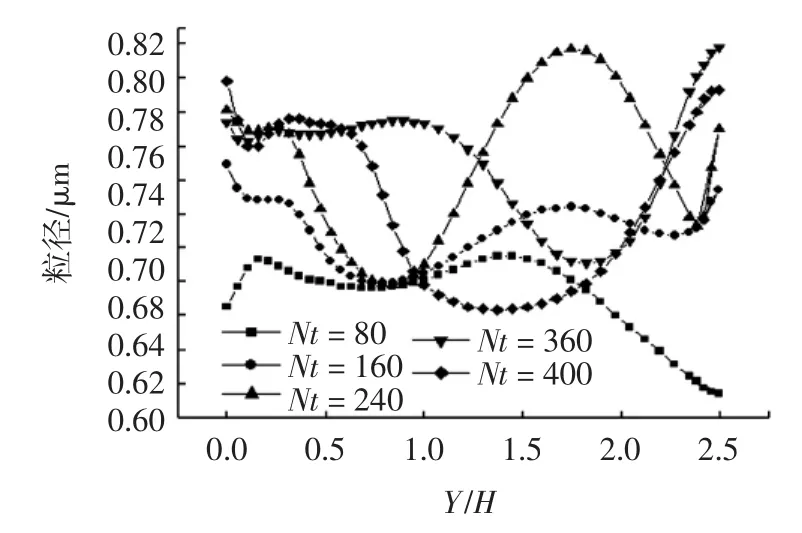
图5 x/H=15截面上粒径随时间的变化Fig.5 Particle size change over time（x/H=15）

核区颗粒的运动状态，增加了颗粒的碰撞机会，整体结果表明流场中的颗粒粒径呈现变大的趋势.

在流动初期流场中的大涡占优势，由于研究的颗粒的St＜＜O（1），此种颗粒对流场的跟随性较好，有些甚至可以直接被涡结构卷吸拖曳进大涡结构的核心区域，涡的卷吸促使颗粒在涡核和整体流场中的停留时间增多；并且伴随涡的合并与破碎，颗粒与涡结构间的相互作用较强，涡结构的变化增加颗粒的碰撞机会，增强颗粒团聚效果.但当Nt＞240后，伴随涡的破碎与合并，涡结构呈现动态稳定，小尺度涡占优势，涡结构变化程度相对较弱，涡结构对颗粒团聚的作用不再有显著提高，颗粒数密度变化较小.

在Re=18 400、St=0.001的条件下，分析整个流场中颗粒团聚效果随时间增长的变化，分析结果见图6.图6表明在Re=18 400的情况下，颗粒数密度随无量纲时间的增大而增大，并且大颗粒数密度增加明显.在Nt=20～Nt=240之间时，流场中涡结构发生明显变化，涡结构对颗粒的团聚作用显著，从图6中的曲线可以看出，随时间的变化颗粒团聚效果增强，颗粒数密度明显增加，在Nt＞240之后的时刻，涡结构处于动态稳定的状态，颗粒数密度变化很小.图7给出了峰值粒径的大小和其百分含量随时间的变化情况，在初始阶段，粒径变化较快，当时间足够长时粒径变化相对平缓.由于所设初始粒径为0.1 um，所以在Nt=20时，峰值为小粒径且百分数含量比其他情况下大很多，当粒径不断团聚长大后，粒径分布近似呈正态分布，总体情况来看，颗粒粒径呈现变大趋势.

图6 颗粒数密度的变化Fig.6 The change of particle number density

3.2 不同St数下颗粒团聚情况

选用颗粒粒径对应的Stokes数为0.001、0.004、0.01和0.016，颗粒的体积分数为7×10-4.不同St数时的涡量场如图7所示，可以看到不同初始St数的颗粒对涡结构的作用不同，当St小于0.01时，涡结构均匀分布在主流体两侧近壁面处，此时颗粒粒径较小跟随性好，进入涡结构核心区，在涡结构内颗粒的浓度增大，增加颗粒的团聚几率；随颗粒团聚，颗粒的粒径变大，颗粒的惯性效果增强，颗粒与涡结构之间的相互作用加强，颗粒加速了对拟序大涡结构的混合破碎作用，大涡逐渐转化为尺度较小涡，流场中的涡的变化变成以尺度较小的涡的变化为主.

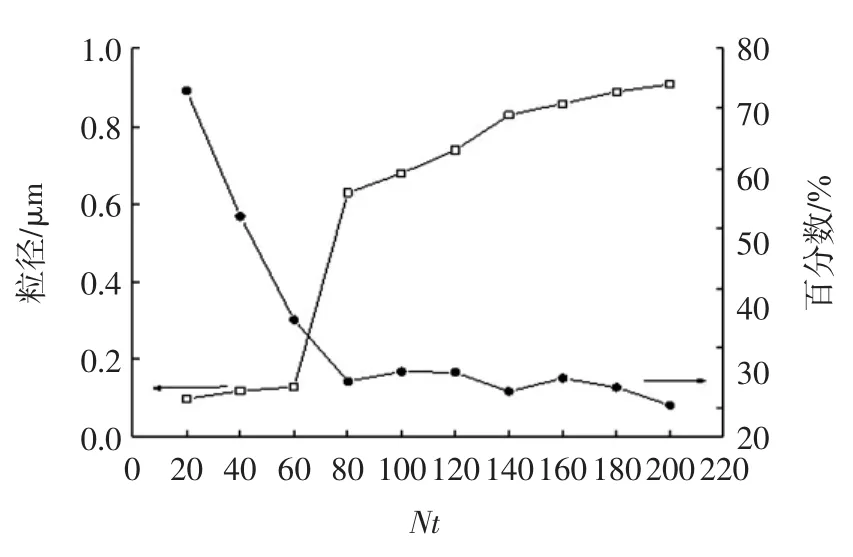
图7 峰值粒径随时间的变化Fig.7 The change of peak diameter over time

随着St的增大，颗粒对涡结构的影响越来越明显，流场中的大涡结构甚至破裂成小尺度的碎片，涡量分布不再规则光滑；与St数较小的相比，St=0.1时涡结构有明显变化，涡结构变小且呈不规则形状，与陈鑫蔚[20]所述吻合.在流场中大涡的生成和演变的过程中，颗粒相运动会出现优先聚集的区域.但是随着流体的发展，初始St数变大时，流场中的涡结构呈现出不规则的小尺度涡结构或碎片的状态，而颗粒粒径随颗粒的团聚不断变大，由于空气动力学尺度的变化，颗粒的空气动力学时间比涡结构的特征时间尺度大得多，St数较大的颗粒，颗粒的惯性大，不容易对流体的变化做出响应，与Eaton[10]所述相符.涡结构对颗粒运动状态的作用减小，颗粒在流场中的浓度分布随之变得比较均匀，流动过程中不再呈现出颗粒富集的区域，绝大部分直接穿过射流中心区向下游运动，颗粒间的碰撞时间相应减少，致使颗粒团聚效果减弱.

由于模型中只考虑颗粒的团聚效果，颗粒减少说明颗粒之间发生了团聚.如图9所示，在流动方向初始粒径颗粒的百分数减少的越多，团聚效果越好.对于St=0.001的情况下，在进入口处，初始颗粒百分比含量下降的较快，由于粒径小被涡结构卷吸的颗粒越多，碰撞机会越多，团聚效果较好，当颗粒团聚长大后，颗粒不易跟随涡结构运动，对涡结构起到破坏作用，从而涡结构尺度变小，对颗粒的卷吸碰撞作用减弱，颗粒团聚效果下降，图9中颗粒百分比含量变化趋于平缓；由图9得随St数的增大，沿流动方向的颗粒百分含量变化越来越小，团聚效果降低.颗粒直径变化程度减小，流场中的颗粒的分布主要是初始粒径大小的颗粒的分布.由于随入口处初始进入槽道的颗粒粒径的增大，颗粒弥散的程度逐渐削弱，大部分颗粒保持原有的运动状态流入下游，并且在初始体积分数相等的情况下颗粒的个数减少，颗粒之间的距离增大，碰撞次数减少，细颗粒物的聚并效果变弱.

图9 不同St下初始颗粒百分比的分布Fig.9 Percentage of initial particle under different St

3.3 不同体积分数下的颗粒团聚情况

为研究颗粒的个数对团聚的影响，选取入口颗粒St为0.001，颗粒的个数采用颗粒占有的体积分数表示，用Vc表示，分别为7×10-5、7×10-4、0.001、0.002、0.01.通过数值模拟得到上述不同体积分数条件下的涡量场，见图10.

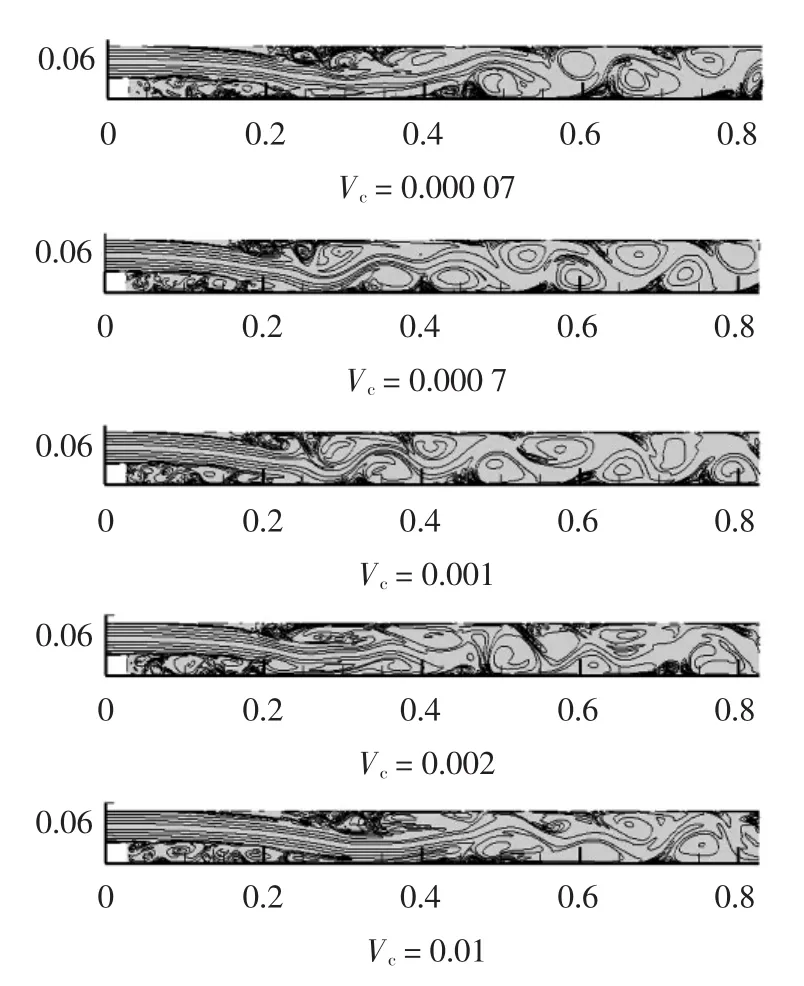
图10 不同Vc的涡量图（Nt=500）Fig.10 Vorticity graph with different Vc（Nt=500）

图10结果表明，在初始粒径较小（如St=0.001）的情况下，随颗粒的体积分数增大，流场的扰动作用加强.当体积分数较小时，即体积分数为7×10-5和7× 10-4的情况，涡结构在上下壁面均匀分布，当体积分数为0.001时，流场涡结构就发生了明显变化，涡结构分布紧凑；当体积分数增加到0.01时，主流体波动范围变小，涡结构不在呈规律性分布，涡结构和主流体区域变窄.

本节计算中选取的St数较小，当颗粒体积分数较少时，流场中颗粒与涡结构有较好的跟随性，颗粒的浓度较小，即颗粒个数较少，致使颗粒之间的碰撞机率降低，颗粒之间的团聚效果不是很好，颗粒与涡结构之间的相互作用不是很强，对涡结构的破碎作用较弱，大涡结构可以保持较长时间；随着颗粒的体积分数增加，颗粒的相对浓度增加，较多的颗粒被卷吸进旋涡内，颗粒的团聚效果增强；但是颗粒与涡结构的相互作用增强，颗粒对涡结构的破坏作用增大，使得下游再形成的涡结构涡量降低较多，而团聚后的颗粒由于惯性增加，较少数量的颗粒进入到下游的涡结构内，导致团聚效果变差.图11表明随初始体积分数的增大，初始粒径的颗粒数密度增大，颗粒的碰撞机率相应增大，在只改变初始体积分数的情况下，颗粒团聚效果随体积分数的增大而增强，但增加初始体积分数到达一定数量时，颗粒聚并效果的变化效果减弱.

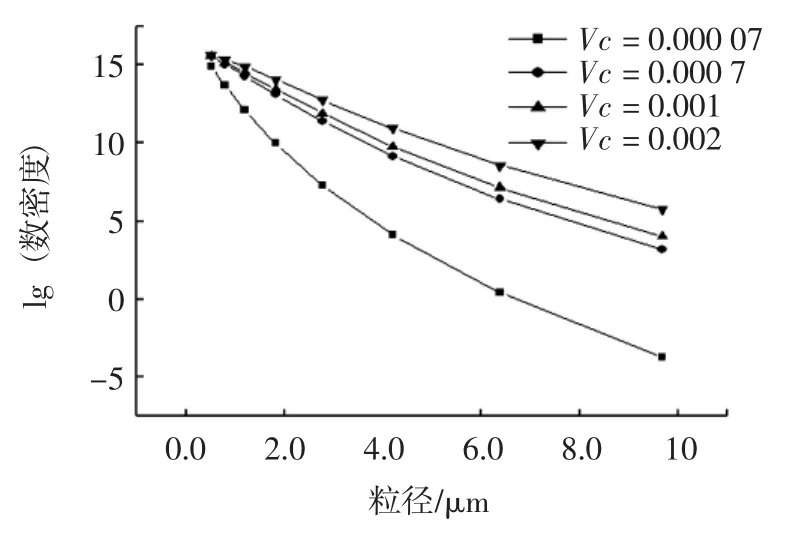
图11 不同体积分数下颗粒数密度的分布Fig.11 The change of particle number density with different Vc

在初始颗粒粒径较小（即St=0.001）的情况下，随颗粒的体积分数增大，较多的颗粒进入到涡结构中，颗粒的团聚效果好；但是随初始体积分数的增大，颗粒对流场涡结构调制作用增强.当体积分数为0.001时，流场涡结构就发生了明显变化，涡结构分布紧凑；当体积分数增加到0.01时，主流体波动范围变小，涡结构不再呈规律性分布，流场涡结构逐渐失去对颗粒的卷吸作用，颗粒团聚效果变得越来越差，表现在图11中，对比同一粒径下颗粒的数密度，变化程度随初始体积分数的增加而减弱.

4 结论

1）在后台阶流动中随无量纲时间的增大角涡回流区变化并不明显，角涡回流区一直处于低涡量区，因此团聚后的颗粒不随流场运动，颗粒停留在角涡区，角涡区成为团聚后颗粒的停滞区.由于流场中涡结构的破碎与合并，流场呈现动态变化，其他截面处颗粒粒径呈现不规律的波动.

2）随St数的增大，粒径变化程度减小，流场中的粒径大小分布主要是初始入口喷入粒径的分布.由于在初始喷入的颗粒直径增大的条件下，颗粒弥散的程度逐渐削弱，大部分颗粒保持原有的运动状态流入下游，并且在初始体积分数相等的的情况下颗粒的个数减少，颗粒的间距增大，碰撞次数随之减少，细颗粒物的聚并效果变弱.

3）本文研究的颗粒体积分数小于10-2数量级，在颗粒体积分数增加的条件下，初始粒径的颗粒个数增多，在只改变初始入口体积分数的情况下，颗粒团聚效果随体积分数的增大而增强，但改变初始加入的体积分数，使其增加到一定限度时，颗粒聚并效果的变化效果减弱.

致谢本文得到我校能源与环境工程学院动力工程领域专业学位研究生创新项目的资助.

[1]Guowei Pan，Shujuan Zhang，et al.Air pollution and children’s respiratory symptoms in sixcities of Northern[J].Respiratory Medicine，2010，104（12）：1903-1911.

[2]Jethro Akroyd，Alastair J Smith，Raphael Shirley，et al.A coupled CFD population balance approach for nanoparticle synthesis in turbulent reacting flows[J].Chemical Engineering Science，2011，66（17）：3792-3805.

[3]Montes I，Rego G，Camblor C，et al.Respiratory disease in aggregate quarry workers related to risk factors and Pi phenotype[J].J Occup Environ Med，2004，46（11）：1150-1157.

[4]颜金培，杨林军.氨法脱硫烟气中气溶胶凝结脱除动力学[J].中国机电工程学报，2011，31（29）：41-47.

[5]赵海波，郑楚光.离散系统动力学演变过程的颗粒群平衡模拟[M].北京：科学出版社，2008：10-50.

[6]Mao D，Edwards J R，Kuznetsov A V，et al.A model for fine particle agglomeration in circulating fluidized bedabsorber[J].Heat and Mass transfer，2002，38（4-5）：379-388.

[7]Alipchenkov V M，Zaichik L I，Solovev A L.Influence of condensation on coagulation of aerosol particles during their Brownian and turbulent motion [J].Heat Transfer Research，2004，35（1-2）：99-107.

[8]Eibeck A，Wagner W.Stochastic interacting particle systems and nonlinear kinetic equations[J].Ann Appl Probab，2003，13：845-889.

[9]Yeoha G，Tub J.Two-fluid and population balance models for subcooled boiling flow[J].Appl Math Model，2006，30（11）：1370-1391.

[10]Miller S，Garrick S.Nanoparticle coagulation in a planar jet[J].Aerosol Sci Tech，2004：38，79-89.

[11]Rigopoulos S.Population balance modelling of polydispersed particles in reactive flows[J].Prog Energy Combust Sci，2010，36：412-443.

[12]王兵，张会强，王希麟，等.湍流分离流动中的颗粒弥散机制[J].清华大学学报（自然科学版），2003，43（11）：1507-1510.

[13]Hogan R C，Cuzzi J N，Stokes and Reynolds number dePendence of Preferential Particle concentration in simulated three-dimensional turbulence[J]. Phys Fluids，2001，13：2938-2945.

[14]Wood A M，Hwang W，Eaton J K，Preferentialeon centration of Particlesin Homogeneous and isotro Pieturbulenee[J].Int J Multi Phase Flow，2005，31：1220-1230.

[15]Elghobashi S E.On predicting particle-laden turbulent flows[J].Appl Sci Res，1994，52：309-329.

[16]Eaton J K，Johnston J P.Turbulent flow reattachment：an experimental study of the flow and structure behind a backward-facing step[R].Standford Univ Rept，1980：MD-39.

[17]Fessler J，Eaton J K.Turbulence modification by particles in a back-ward-facing step flow[J].J Fluid Mech，1999，394：97-117.

[18]武生智，赵玉军.二维气固两相后台阶流动的大涡模拟[J].中国沙漠，2011，31（5）：1093-1097.

[19]Moin H P，Kim J.Direct numberical simulation of turbulent flow over a backward-facing step[J].Fluid Mech，1997，330：349-374.

[20]陈鑫蔚，樊建人.考虑颗粒碰撞的三维混合层直接数值模拟[J].工程热物理学报，2010，31（8）：1327-1330.

[责任编辑 田丰]

PBM coupled simulation of aggregation in backward-facing step

LU Mingtao,CHEN Zhanxiu,YANG Li,LI Yang
（School of Energy and Environmental Engineering,Hebei University of Technology,Tianjin 300401,China）

The large eddy simulation(LES)coupled Population Balance Model(PBM)was used to simulate the gas-solid two-phase flow through backward-facing step.The vortex structures in flow field were in good agreement with the experimental results.Based on this,it is found that the vortex structureshave effect on particle diffusion and particle aggregation under different sections and Stokes number and volume fraction(Vc).When the Stokes of the particles is smaller,they followthe vortex structure tightly,and alsodestroys the vortex structure.This has lead to abetter agglomeration among particles at the beginning of the flow field,while the destruction of the vortex structure has gradually weakened the aggregation among particles.The greater volume fraction of particles has caused greater damage to the vortex structure, hencethe agglomeration effection has been gradually weakened in flow.

LES;PBM;backward-facing step;particle aggregation;vortex structure

X513

A

1007-2373（2017）02-0092-07

10.14081/j.cnki.hgdxb.2017.02.016

2016-12-28

河北省高等学校科学技术研究项目（ZD2015128，ZD2016163）.

卢明涛（1991-），女，硕士研究生.通讯作者：陈占秀（1969-），女，副教授，2963790166@qq.com.