改进的Beta过程因子分析图像修复算法

苑焕朝，马杰，樊金光

（1.河北工业大学电子信息工程学院，天津300401；2.天津市电子材料与器件重点实验室，天津300401）

改进的Beta过程因子分析图像修复算法

苑焕朝1，2，马杰1，2，樊金光1，2

（1.河北工业大学电子信息工程学院，天津300401；2.天津市电子材料与器件重点实验室，天津300401）

图像修复是利用图像已知信息对图像破损区域进行填充修复的过程，而非参贝叶斯技术在图像稀疏表示中被认为是一种有效的字典学习方法，作为一种有效的非参贝叶斯算法，基于Beta过程因子分析算法（BPFA）在去噪、修复以及压缩感知方面有很广泛的应用.然而现有的BPFA算法在对含噪的破损图像修复时收敛速度慢，针对这个问题本文在BFPA算法更新字典时与K-SVD算法相结合，提出一种基改进的BPFA学习算法，改进算法利用K-SVD算法简单收敛速度快的特点，在原有算法更新参数时，利用OMP稀疏编码更新字典候选集以达到提高算法的收敛速度的效果.得到的结果表明本文算法能够更好地修复含噪破损图像获得较好的视觉效果.

图像修复；贝叶斯；字典学习；Beta过程；K-SVD

0 引言

随着科学的进步，信息的传输也变得越来越重要，而图像作为最主要的信息传输载体变得尤为重要，然而很多因素都会引起图像的破损，图像修复就是利用已有的图像信息对破损区域填充修复的过程，图像修复在修补破损区域、移除目标或遮挡、文物保护、影视特技制作和图像压缩等方面有着重大的研究意义.

现有的图像修复技术主要包括以下3类：基于纹理合成的方法、基于偏微分方程（PDE）的方法和基于稀疏表示的方法[1].基于偏微分方程的图像修复算法最开端是由Bertalmio等人提出的BSCB修复模型[2]，BSCB主要是利用破损处的边缘信息根据数据等照线向破损区域扩散修复破损点.随后Shen和Chen等人提出了经典的TV算法[3]，TV算法主要是利用Euler-Lagrange方程进行扩散修复；为了获取更好的修复效果，2001年chen等在TV算法的基础上提出了一种CDD模型[4]，该模型在进行修复时不再只依赖等照线进行修复，还将图像曲率信息考虑进去，结合梯度与曲率对图像进行扩散修复.基于纹理合成的图像修复算法是一种适合大面积破损区域修复的算法，2004年Criminisi等人提出了一种基于样本块的纹理合成方法[5]，该算法先确定修复区域的优先级，再将破损块与已知区域进行匹配，将相似度最高的图像块填补到破损处.基于稀疏表示的图像修复算法[6]是利用过完备字典以及破损图像中有效信息进行稀疏编码再对图像进行修复的过程.

文献[7]利用基于beta过程因子分析算法（简称BPFA）构建和学习冗余字典从而达到图像修复的效果.在图像修复过程中当图像存在噪声时BPFA算法无需输入噪声方差，在字典学习过程中会逐步去除噪声，由此可见BPFA算法比一般的图像修复算法更具有广泛的适用性.然而BPFA算法也存在一些弊端，BPFA算法在进行修复时运行时间过长，收敛速度过慢，而且当图像存在噪声污染时，图像修复效果略差.

本文根据BPFA收敛速度慢的问题，提出了将BPFA算法与K-SVD字典学习算法相结合，利用KSVD算法简单收敛速度快的特点，在原有算法更新参数时，利用OMP稀疏编码优化字典候选集以达到提高算法收敛速度的效果.通过选取不同图像进行实验研究，结果表明改进算法比原算法峰值信噪比要高出0.2～0.4 dB，而且根据图像的不同运行时间比原算法快100 s左右，由实验数据证明改进算法不但有更好的收敛速度而且在对含噪图像修复方面具有良好的性能.

1 字典学习模型

2 BPFA算法模型

近几年，非参数贝叶斯算法[10]在各个方向都得到了广泛的应用.BPFA算法就是基于Beta过程的非参贝叶斯字典学习算法，BPFA通过引入beta过程利用数据之间的结构先验知识生成矩阵Y，从而使得矩阵Y具有更好的稀疏性.

BPFA算法需要通过准确表示X时所需要的字典D列数来推断M的大小，为了达到这个目的，先假设公式（1）中然后通过推断字典D所包含的列数来近似的推断字典大小.由于Y∈ RK×N是稀疏的，即Y中只有有限项是非零的，因此再通过字典D表示Y时只有一小部分原子被使用.

beta过程是一种利用结构先验知识的方法，BPFA利用双参数beta来获取数据的稀疏性[6、11].定义双参数Beta过程为其中满足一致分布则beta过程可以写为：

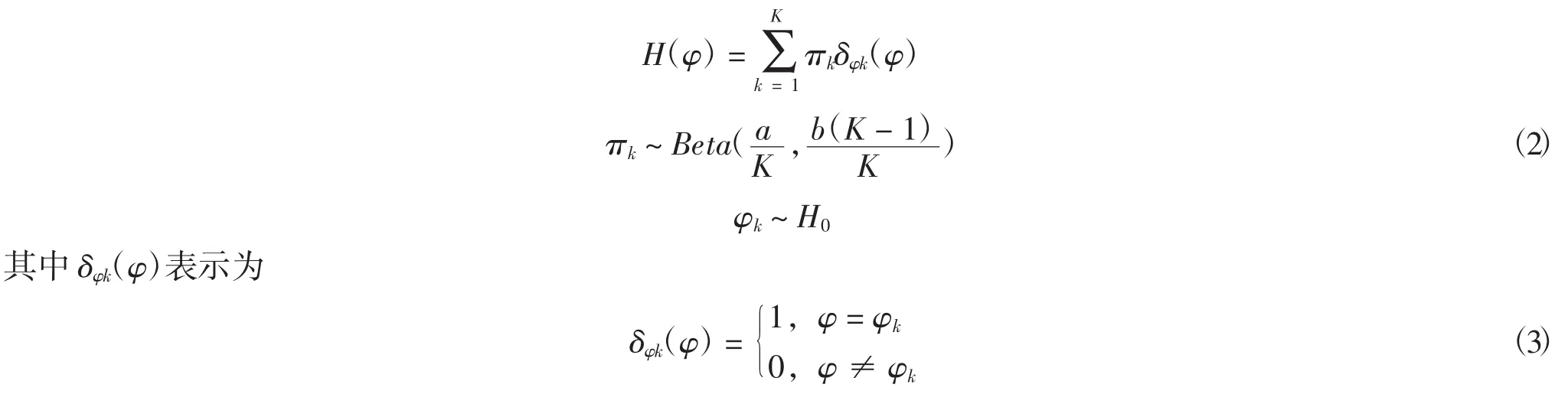
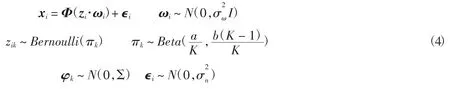
3 K-SVD字典学习算法

K-SVD算法是由Elad和Aharon等人于2006年提出的一种经典字典学习算法[12]，K-SVD在更新字典时是依次对字典中的原子进行更新，并且在更新原子时，对应的更新其稀疏表示系数，因此K-SVD是一种快速且有效的字典学习算法[13].

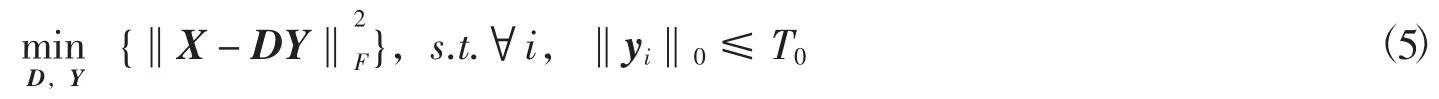
第2步更新字典D，K-SVD在更新字典时依次对字典中每列进行更新，令表示字典D的第j列，则此时信号的分解形式可以表示为

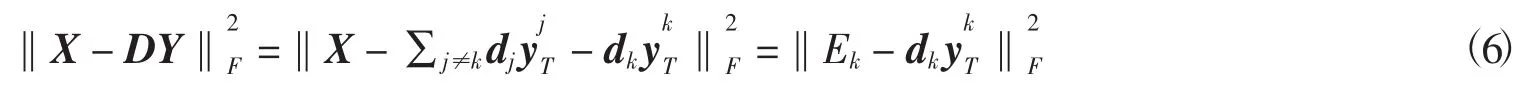
将上式带入公式（6）得

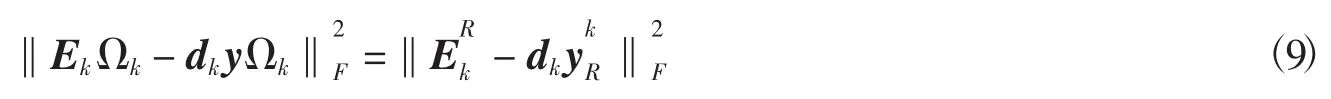
K-SVD算法具有灵活度高，收敛速度快的优点，缺点是容易陷入局部最优，学习到的字典易受样本集选取的影响.

4 改进算法

本文针对现有BPFA算法在对含噪的破损图像修复时收敛速度慢的问题提出一种改进的BPFA学习算法，改进算法利用K-SVD算法简单收敛速度快的特点，在原有算法更新参数时，利用OMP稀疏编码更新字典候选集，使得每次更新结束后能够得到更好的学习字典，从而达到提高算法收敛速度的效果.

4.1 改进算法求解过程

在改进算法中，首先根据破损图像X利用beta过程初始化稀疏系数以及过完备字典D的构建，完成参数的初始化，之后根据每次更新得到的噪声大小和字典利用K-SVD进行字典候选集更新，再利用变分贝叶斯算法更新字典以及权重系数、二值矩阵，更新图像块，最终输出修复图像.

改进算法的求解是利用变分贝叶斯算法进行快速求解.变分贝叶斯的求解过程是一个不断迭代更新的过程.

4.1.1 更新字典候选集

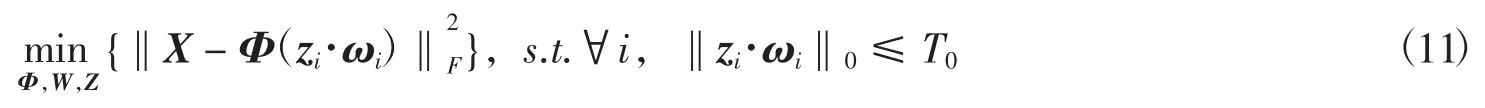
编码完成通过优化信号分解式（6）完成Φ的更新

4.1.2 更新Z

定义

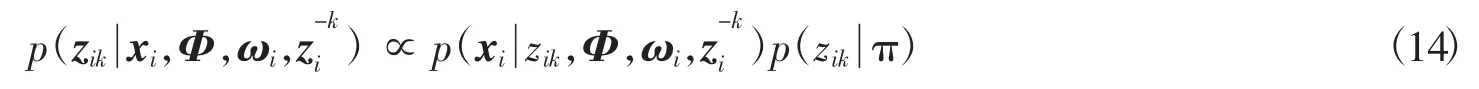
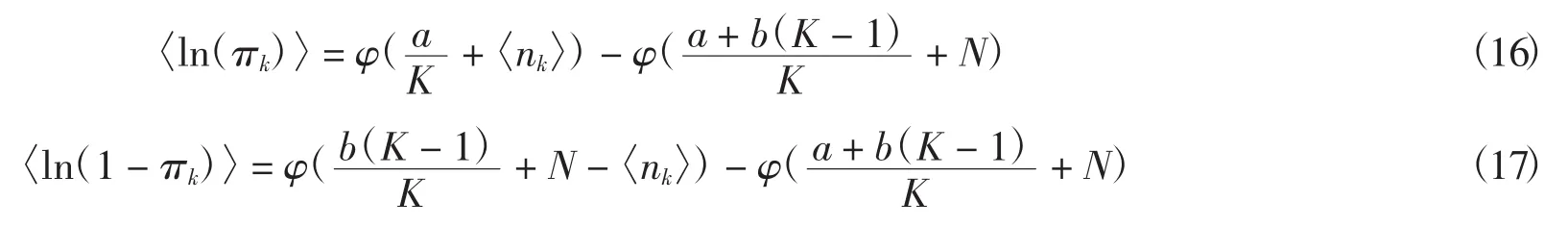
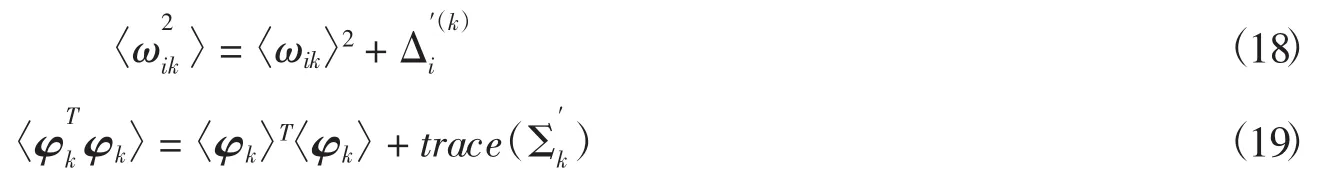
4.1.3 更新π

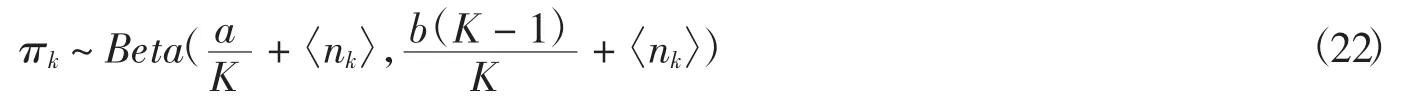
4.1.4 更新Φ

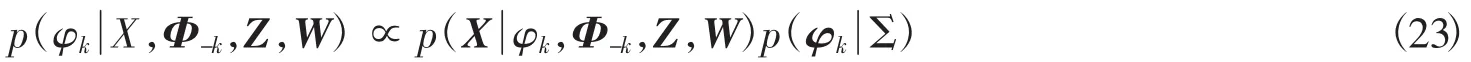
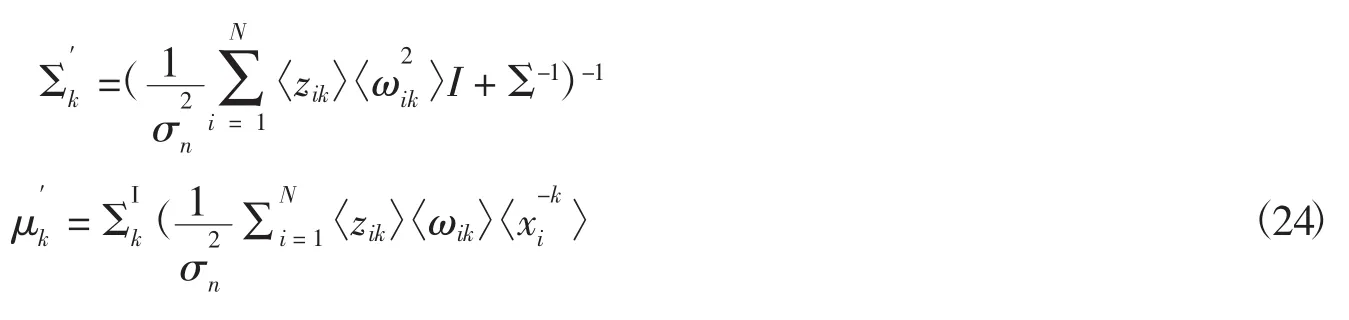
4.1.5 更新W

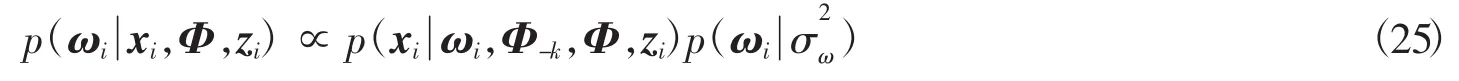
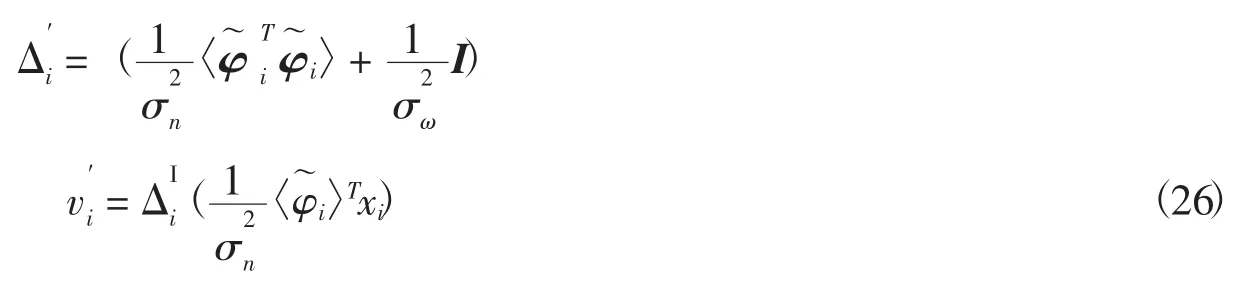
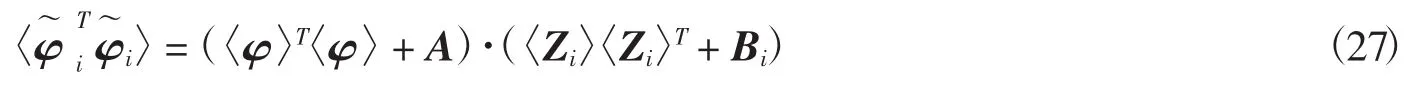
其中A，B表示如下

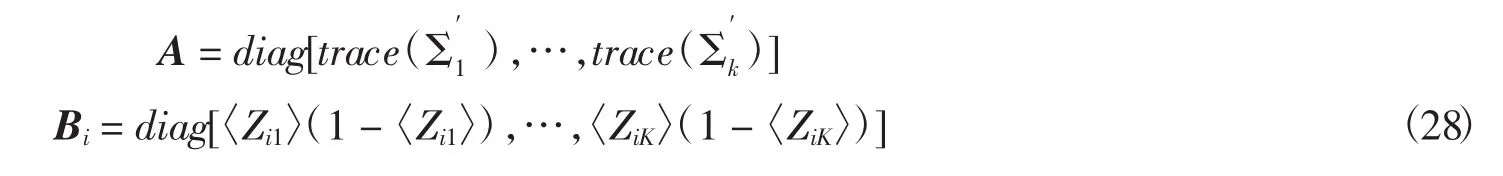
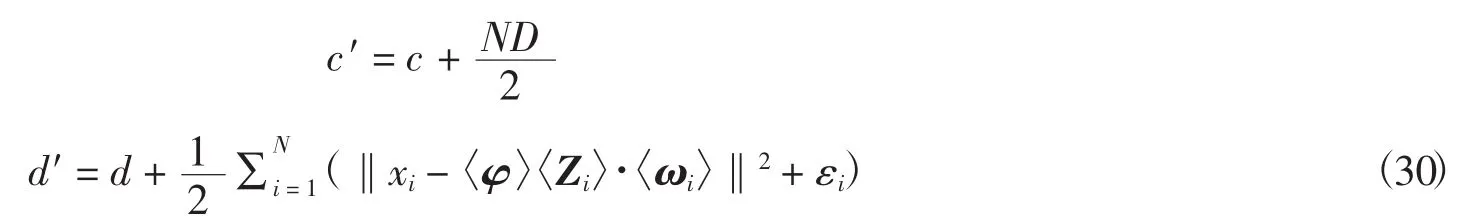
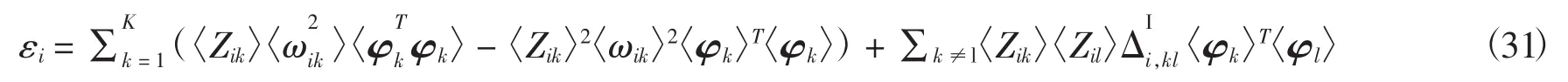
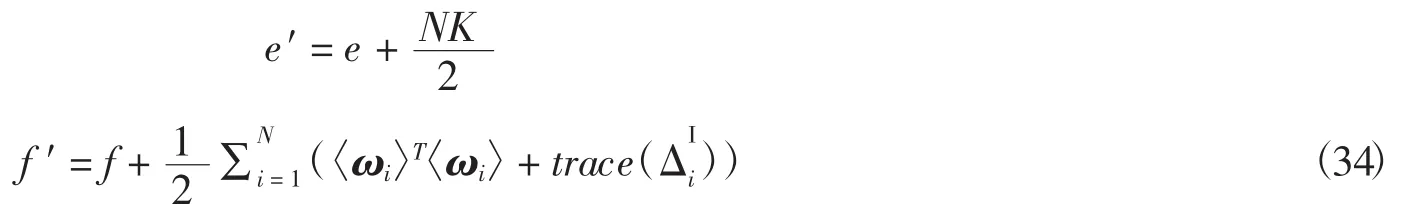
4.2 改进算法步骤

改进算法步骤如下

Step2初始化：设置初始字典大小K，以及字典候选集Φ以及Z，W.

while not converged do

Step3利用OMP算法进行稀疏编码求解公式

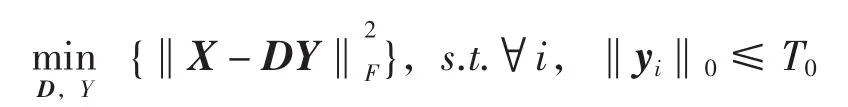
Step5利用Z的分布式更新二值矩阵Z.

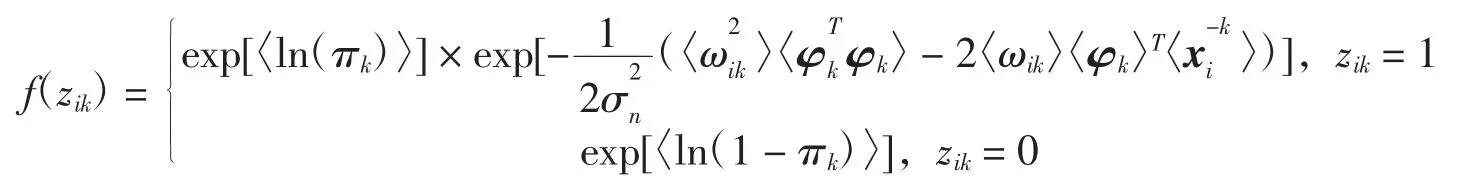
Step7通过求解Φ的均值以及方差更新Φ.

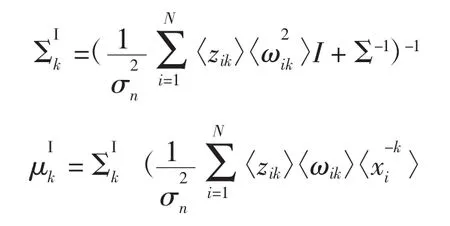
Step8通过求解W的均值以及方差更新W

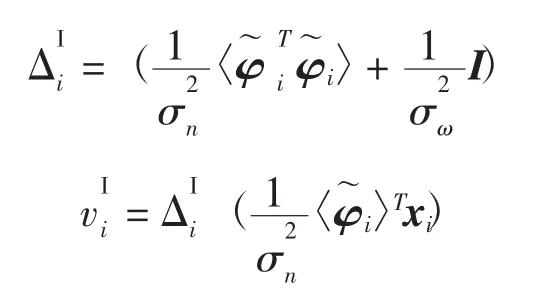
end while

5 实验仿真与结果分析

为检验本文方法的有效性，利用CPU为2.4 GHz，内存为8 GB的计算机，通过MATLAB R2015b编程进行仿真实验.

仿真过程多幅采用256×256的图像进行实验分析，此处选取lena图像、pirate图像、barbara图像为例进行实验分析.为获得噪声图像，给图像加入均值为0，方差为25 dB的高斯白噪声，并查阅文献选取文字覆盖作为破损对含噪图像进行破损处理，破损部分包含像数4 838个，占总像素的7.4%，在加入噪声以及破损后lena、pirate、barbara 3幅图像峰值信噪比分别为17.036 7、16.918 1、16.874 9.选设定字典块大小为8×8利用改进的BPFA算法对该含噪破损图像进行修复，并设置最大迭代次数n=64.为了与改进算法进行对比，引入传统的TV修复方法作为对比方法.

图1为TV修复算法、BPFA算法和改进算法对256×256的lena、Pirate、barbara含噪破损图像的修复效果图.由图1可以看出BPFA算法与改进算法修复效果比之传统的TV修复算法要好，而改进的修复算法比原有的BPFA算法略好一些.

图1 不同算法对不同图像修复效果对比Fig.1 The inpainting resultsbetween different algorithm

为了更清楚的分析实验结果，表1给出了3种算法的恢复性能，其中PSNR是指图像修复后的峰值信噪.

表1 测试图像的恢复性能Tab.1 image recovery performance betweendifferent algorithm

由表1可以看出TV修复算法在图像修复方面用时较少基本都在1s以内，但修复效果不理想，在同等情况下比BPFA算法要小1.5～2 dB左右，由此可以看出BPFA算法在图像修复中的优势，而本文算法与原有的BPFA算法相比平均运行时间缩短了100～200 s左右，大大的提高的收敛速度，而且在同等情况下本文算法比原有算法峰值信噪比平均高出0.2 dB左右，证明了改进算法性能的优势.

图2是迭代次数与运行效果的关系图，由图2可以看出，随着迭代次数增加，传统的BPFA算法需要更多的迭代次数才能达到与本文相似的效果，而本文改进算法在迭代次数较少时已经超过原有算法快速的得到收敛.

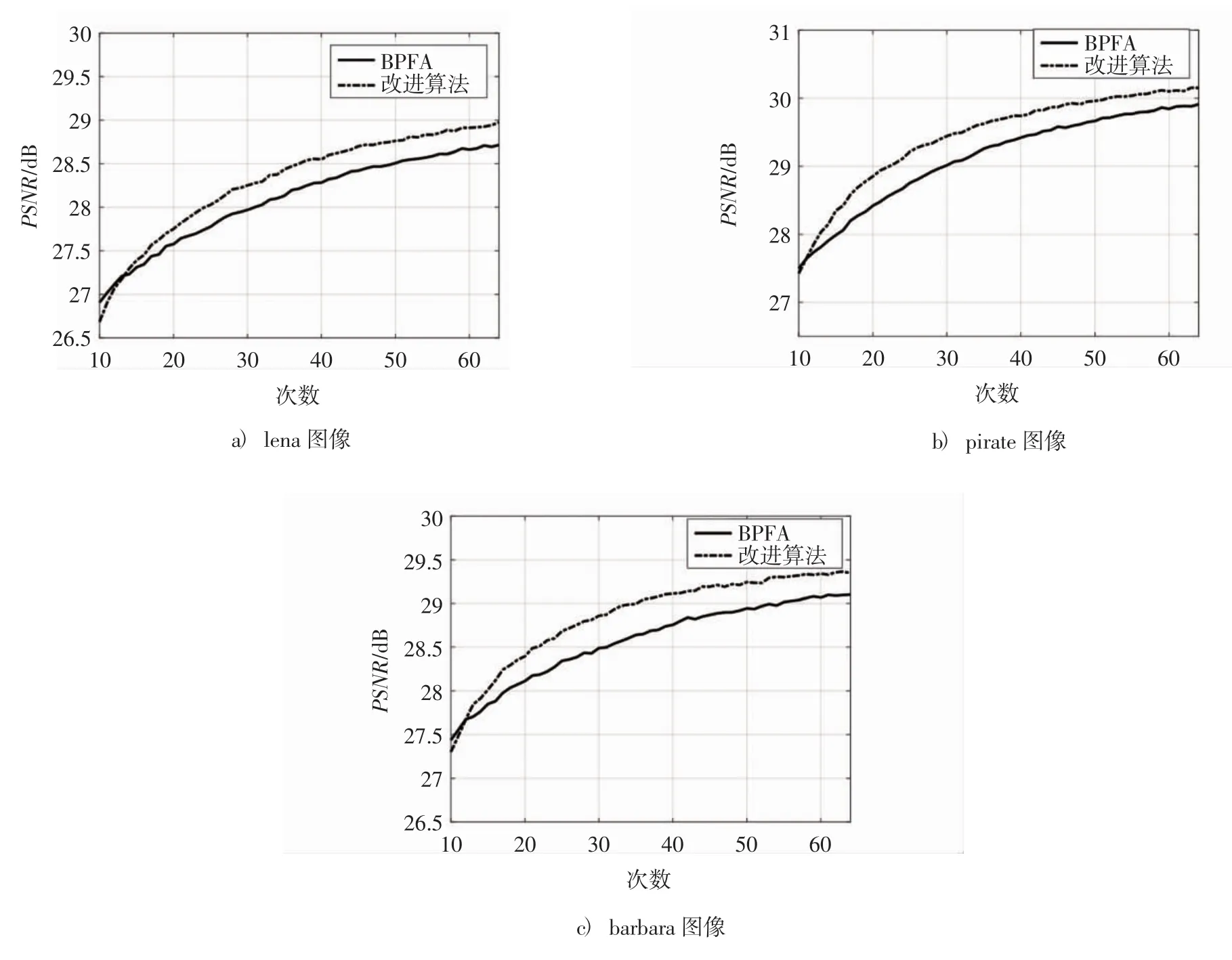
图2 迭代次数与运行效果的关系Fig.2 The relationship between iterations and performance

图3是迭代次数与运行时间的关系图，由图3可以看出，随着迭代次数增加，传统的BPFA算法虽然呈波浪趋势，但总的趋势是在不断增加，而本文改进算法几乎在每次迭代时运行的时间都要比原有的算法用时少，并且改进算法在修复过程中较原有算法增长趋势稳定.

6 结论

本文研究了1种改进的BPFA图像修复方法，该算法可以更好的修复存在噪声污染的破损图像.该算法是将BPFA图像修复算法和K-SVD字典学习算法相结合，使含有噪声的破损图像得到很好的修复.并且改进的BPFA算法有效的提高算法的收敛速度，并且获得较高的峰值信噪比.通过仿真证明本文方法能够快速、有效地修复含噪图像中的破损区域，提高了图像的修复效果.

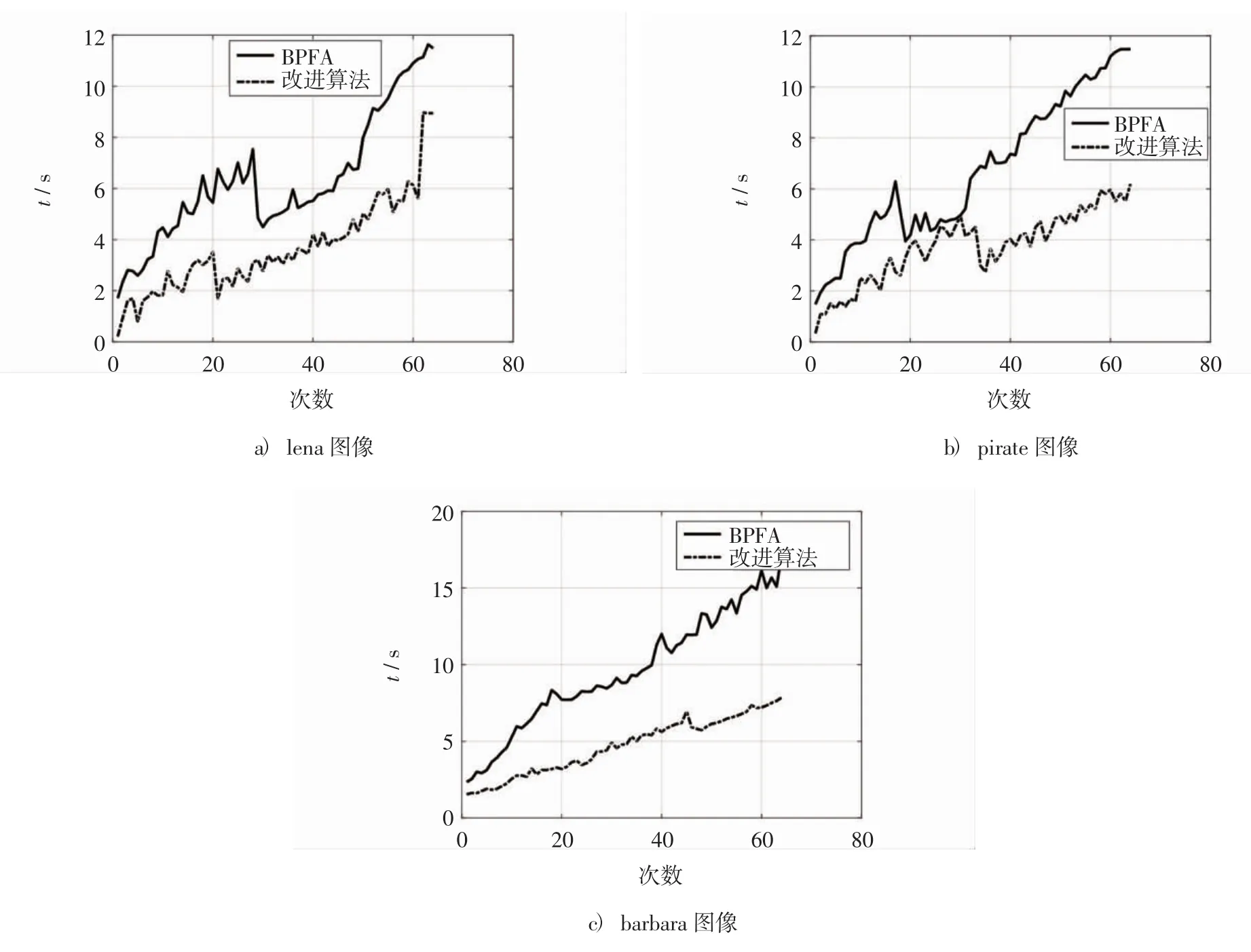
图3 迭代次数与运算时间的关系Fig.3 The relationship between iterations and times

[1]尹忠科，解梅，王建英.基于稀疏分解的图像去噪[J].电子科技大学学报，2006，35（6）：876-878.

[2]Marcelor Bertalmio，Luminita Vese，Guillermo Sapiro，et al．Simultaneous texture and structure image inpainting[J].IEEE Trans on Image Processing，2003，12（8）：882-889.

[3]Chan T，Shen J.Mathematical models for local non-texture inpainting[J].SIAM Journal of Applied Mathematics，2001，62（3）：1019-1043.

[4]Tony F Chan，Jian-hong，Nontexture inpainting by curvature-driven diffusions（CDD）[J].Journal of Visual Communication and Image Representation，2001，12（4）：436-449.

[5]Criminisi A，Perez P，Toyama K.Region filling and object removal by exemplar-based image inpainting[J].IEEE Transactions on Image Processing，2004，13（9）：1200-1212.

[6]党宏社，张娜，白梅.基于贝叶斯压缩感知与形态学成分分析的图像修复方法研究[J].计算机应用研究，2015，32（5）：1572-1575.

[7]Paisley J，Carin L.Nonparametric factor analysis with beta process priors[M].Proc.International Conference on Machine Learning，2009.

[8]张志伟，马杰，夏克文，等.一种应用于图像修复的非负字典学习算法[J].光电子激光，2014，25（8）：1613-1619.

[9]任澍，唐向宏，康佳伦.纹理和边缘特征相结合的图像修复算法[J].计算机辅助设计与图形学学报，2013，25（11）：1682-1693.

[10]刘帅.基于结构信息和稀疏贝叶斯学习的图像去噪[J].火控雷达技术，2015，44（4）：12-18.

[11]Thibaux R，Jordan M I.Hierarchical beta processes and the indian buffet process[M].Proc.International Conference on Artificial Intelligence and Statistics，2007.

[12]Michal Aharon，Michael Elad，Alfred M.Bruckstein.K-SVD：design of dictionaries for sparse representation[C]//Proceedings of SPARS，2005：9-12.

[13]黄江林，刘红，陶少杰.一种改进的基于K-SVD字典的图像修复算法[J].安徽大学学报，2013，37（3）：69-74.

[责任编辑 代俊秋]

An improved imageinpainting algorithm based on Beta process factor analysis

YUAN Huanchao1，2,MA Jie1，2,FAN Jinguang1，2
（1.School of Electronic and Information Engineering,Hebei University of Technology,Tianjin 300401,China;2.Key Laboratory of Tianjin Electronic Materials and Devices,Tianjin300401,China）

Imageinpainting is the process to fill and repair the damaged area of images based on the given information of the images,and Nonparametric Bayesian technique is known as an effective dictionary learning method in image sparse representation.As an effective method of Nonparametric Bayesian,Beta process factor analysis(BPFA)is widely used in the aspects of denoising,repair and compressed sensing.However,the convergence rate of existing BPFA is slow when repairing the damaged images with noise.In order to increase the convergence rate,an enhanced BPFA learning algorithm is proposed,the K-SVD algorithm is combined with BPFA algorithm when updating the dictionary,which means that when updating parameters,OMP algorithm is used to update dictionary candidate set to increase the convergence rate because K-SVD algorithm is simple and has fast convergence rate.The results show that the enhanced algorithm can repair the images better and obtain a preferable visual effect.

imageinpainting;Bayesian;dictionary learning;Beta process;K-SVD

TP391.9

A

1007-2373（2017）02-0017-09

10.14081/j.cnki.hgdxb.2017.02.004

2016-12-08

国家自然科学基金（61203245）

苑焕朝（1990-），男，硕士研究生.通讯作者：马杰（1978-），男，教授.