非齐次树上m重非齐次马氏信源的Shannon-McMillan定理

金少华，刘娇，李小雪，于海荣

（河北工业大学理学院，天津300401）

非齐次树上m重非齐次马氏信源的Shannon-McMillan定理

金少华，刘娇，李小雪，于海荣

（河北工业大学理学院，天津300401）

树指标随机过程已成为近年来发展起来的概率论的研究方向之一.强极限定理一直是国际概率论界研究的中心课题之一.本文利用相对熵密度和随机条件熵的概念，通过构造适当的辅助非负鞅，将Doob鞅收敛定理应用于几乎处处收敛的研究给出了非齐次树上m重非齐次马氏信源的一类Shannon-McMillan定理.

非齐次树；鞅；Shannon-McMillan定理；马氏信源；概率空间

0 引言

树模型近年来已引起物理学、概率论及信息论界的广泛兴趣.树指标马尔科夫链场的出现和发展具有重大的实际意义，一方面它给统计物理提供了严格的数学工具，另一方面它也大大扩充了概率论的研究领域[1].关于树上马尔可夫链场的早期研究见Spitzer[2]及其所引文献.Benjamini和Peres[3]给出了树指标马尔可夫链的定义并研究了其常返性.强极限定理一直是国际概率论界研究的中心课题之一.Penmantle证明了齐次树上PPG不变且遍历的随机场的一个弱大数定律及混合性质[4].文献[5]研究给出了Bethe树上非齐次马尔科夫随机场的一类强偏差定理.文献[6]研究给出了关于齐次树上渐进奇偶马氏链的若干强大数定律.文献[7]研究给出了二叉树上非齐次分支马氏链的强大数定律和熵遍历定理.文献[8]研究给出了树上路径过程的随机路径条件概率的强极限定理．文献[9]研究给出了可列非齐次马氏链的强极限性质.文献[10]研究给出了一类非齐次树上非齐次马氏链的若干强偏差定理.本文首先构造了一类非齐次树，是对现有非齐次树的推广，然后利用相对熵密度和随机条件熵的概念，通过构造适当的辅助非负鞅，将Doob鞅收敛定理应用于几乎处处收敛的研究，研究给出了非齐次树上m重非齐次马氏信源的一类Shannon-McMillan定理.

1 基本概念

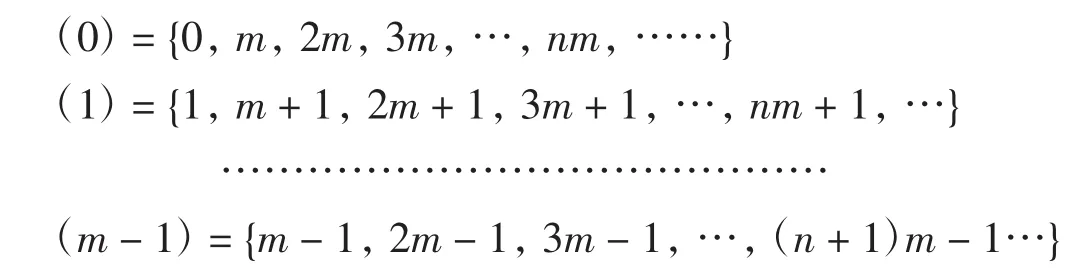
在上述定义下，则树T上的非齐次马尔科夫链的联合分布为

定义3设

2 Shannon-McMillan定理

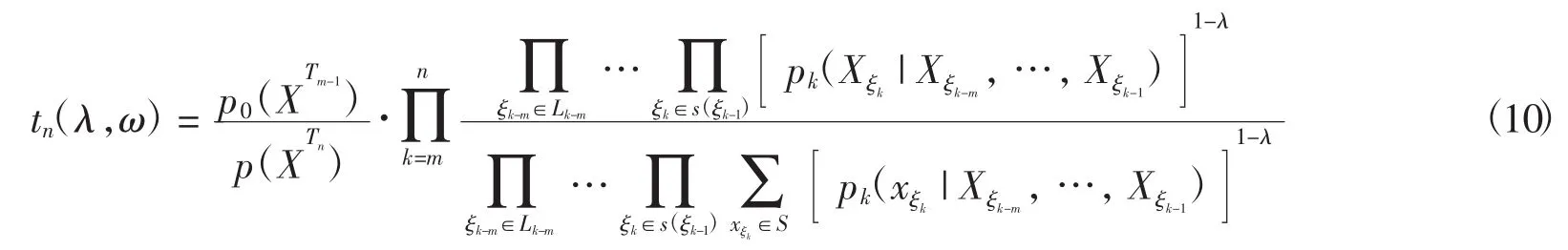
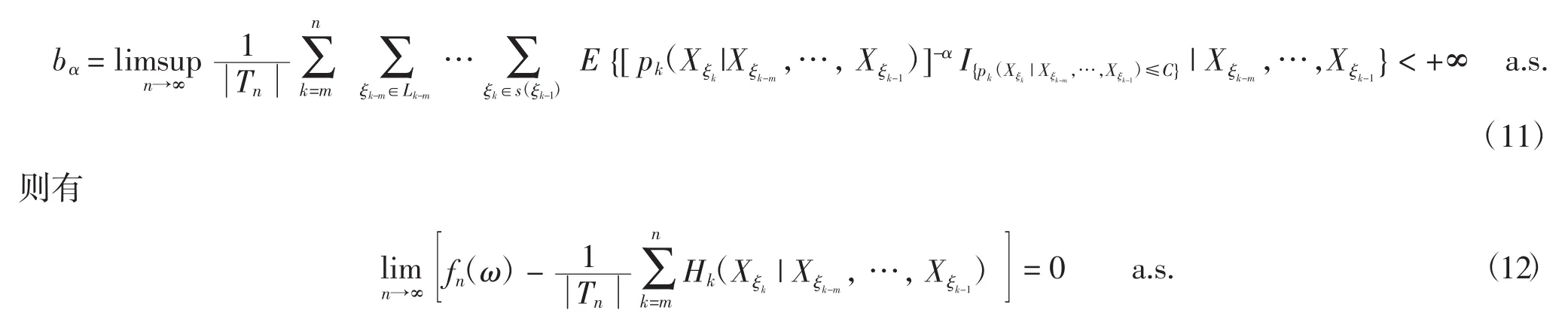
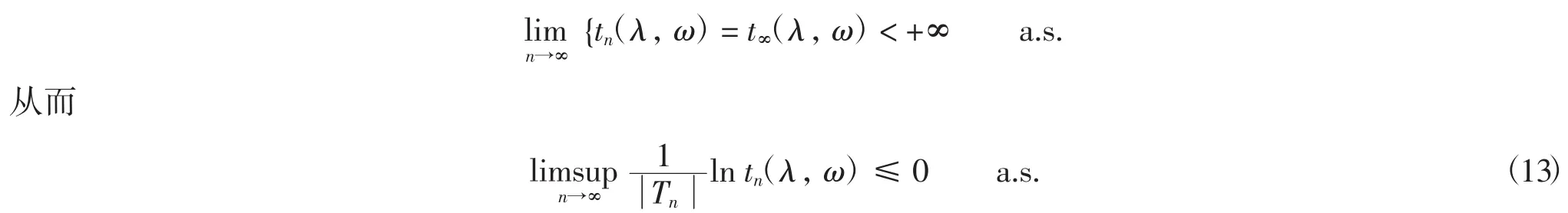
由式（10）与式（13），有

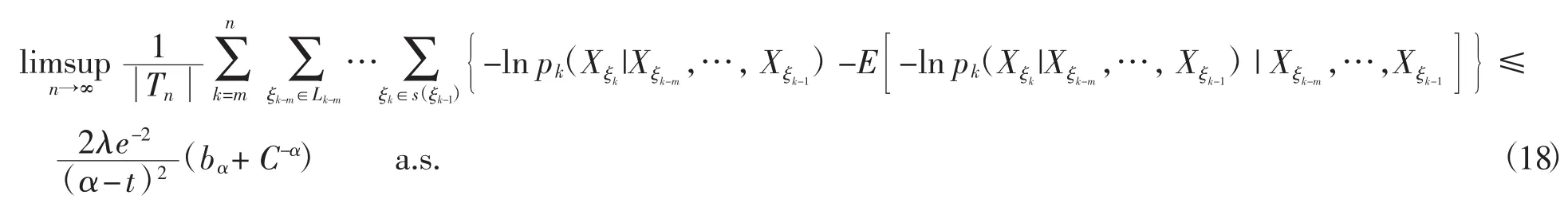
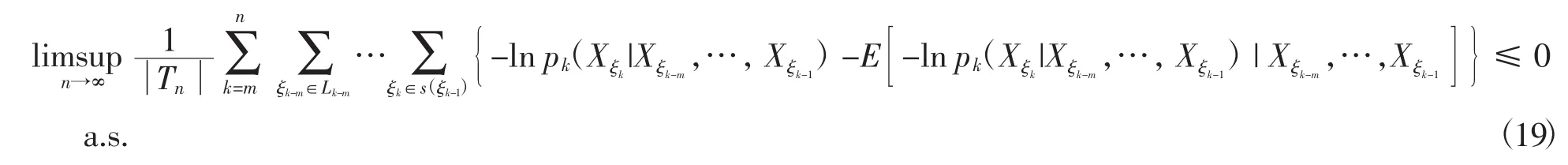
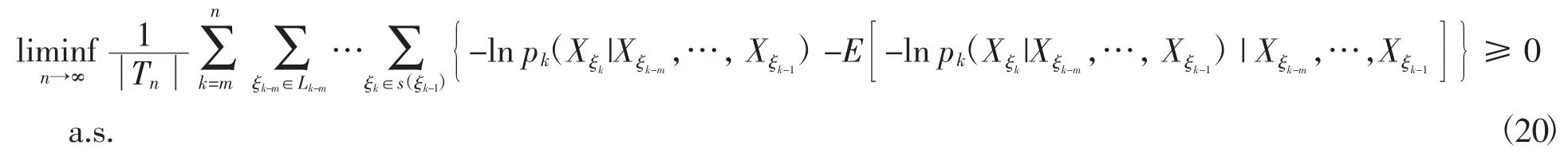
由式（19）与式（20）有

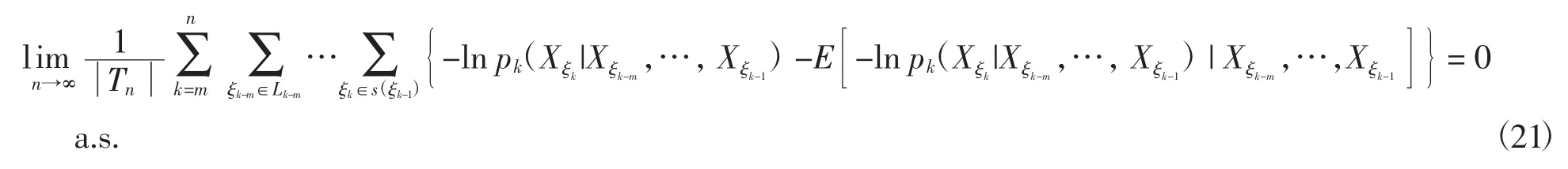
又由式（9），有

于是由式（8）与式（21），有

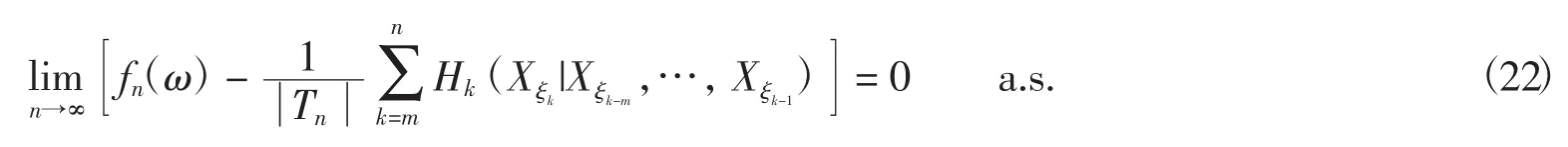
从而定理1证毕.

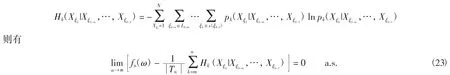
证在定理1中取0<α<1，则有

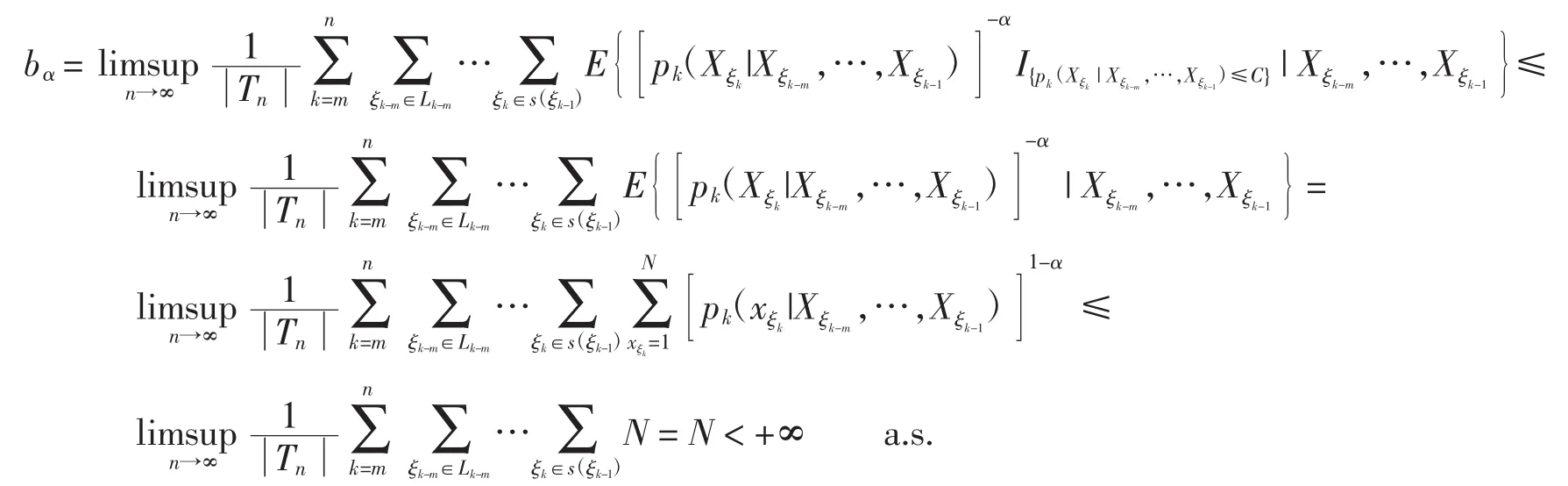
所以式（11）成立.由式（12）即得式（23）成立.

[1]陈木法.随机场概论[J].数学进展，1989，18（3）：294-322.

[2]Spitzer F.Markov random fields on an infinite trees[J].Ann Probab，1975，3：387-398.

[3]Benjamini I，Peres Y.Markov chains index by trees[J].Ann Probab，1994，22：219-243.

[4]Penmantle R.Automorphism invariant measure on trees[J].Ann Probab，1992，20：1549-1566.

[5]Yang W G.A class of deviation theorems for the random fields associated with non-homogeneous Markov chains indexed by a Bethe tree[J].Stochastic Analysis and Applications，2012，30（2）：220-237.

[6]Yang Weiguo，Zhao Yang，Pan Heng.Strong laws of large numbers for asymptotic even-odd Markov chains indexed by a homogeneous tree[J].Journal of Mathematical Analysis and Applications，2014，410（1）：179-189.

[7]Dang Hui，Yang Weiguo，Shi Zhiyan.The Strong Law of Large Numbers and the Entropy Ergodic Theorem for Nonhomogeneous Bifurcating Markov Chains Indexed by a Binary Tree[J].IEEE Trans Inf Theory，2015，61（4）：1640-1648.

[8]韩大钊，石志岩，杨卫国．树上路径过程的随机路径条件概率的强极限定理[J]．数学杂志，2015，35（2）：462-468.

[9]张泓知，郝瑞丽，叶中行，等.可列非齐次马氏链的强极限性质[J].应用概率统计，2016，32（1）：62-68.

[10]金少华，赵静，贺雅萍.一类非齐次树上非齐次马氏链的若干强偏差定理[J].数学的实践与认识，2016，46（18）：251-257.

[责任编辑 杨屹]

Shannon-McMillan theorem of m ordered non-homogeneous Markov information source on a non-homogeneous tree

JIN Shaohua,LIU Jiao,LI Xiaoxue,YU Hairong
（School of Sciences,Hebei University of Technology,Tianjin 300401,China）

In recent years,tree indexed stochastic process has become one of the research directions in the probability theory.The strong limit theorem has been one of the central issues of the international probability theory.In this paper,by applying the concept of the relative entropy density and the random condition entropy,and through constructing an appropriate non-negative martingale,Shannon-McMillan theorem of m ordered non-homogeneous Markov information source on a non-homogeneous tree is given.

non-homogeneous trees;martingale;Shannon-McMillan theorem;Markov information source;probability space

O211.4

A

1007-2373（2017）02-0026-06

10.14081/j.cnki.hgdxb.2017.02.005

2016-07-02

河北省高等学校科学技术研究重点项目（ZD2014051）；河北省高等教育教学改革研究与实践项目（2016GJJG024）

金少华（1965-），男，教授．