基本载荷作用下橡胶类材料的超弹性力学性能分析

桑建兵，刘彦勇，邢素芳，王静远，付双建

（河北工业大学机械工程学院，天津，300130）

基本载荷作用下橡胶类材料的超弹性力学性能分析

桑建兵，刘彦勇，邢素芳，王静远，付双建

（河北工业大学机械工程学院，天津，300130）

基于有限变形的基本理论，对基本载荷作用下橡胶类材料的超弹性力学性能进行了分析.在高玉臣所提出的橡胶类材料的本构模型的基础上，给出了1种新的不可压缩超弹性应变能函数.引入参数α，当n=1且α=1时，新模型转化为Mooney-Rivlin模型，而当n=1且α=0时，新模型转化为Neo-Hookean模型.利用新的本构关系对橡胶类材料在单轴拉伸以及受内压膨胀2种基本载荷作用下的超弹性力学性能进行了研究，分析了本构参数对单轴拉伸和内压膨胀的影响，指出本构参数n为材料的强化参数，橡胶圆管受内压膨胀时存在失稳现象，其稳定性不仅依赖于本构参数n而且与本构参数α相关.

橡胶类材料；本构关系；有限变形理论；单轴拉伸；内压膨胀

0 引言

从20世纪40年代开始，弹性材料的有限变形理论得到了很大的发展.所得出的有意义理论结果和许多实验验证的结果被广泛地应用于描述橡胶类材料的物理行为和工程领域.弹性材料有限变形的数学理论的本质是非线性的，在理论和应用中所遇到的数学方面的困难是可想而知的.近年来，有许多力学工作者用数学和数值分析方法对许多有限弹性理论的非线性问题和技术难题进行了研究.在研究中，人们越来越认识到建立反映橡胶类材料变形特征本构模型是解决问题的核心，选取简单而适用的描述橡胶类材料的本构模型，决定着数值分析方法的精确性和得出结果的可用性[1-5].

目前，人们越来越关注橡胶类材料本构模型的建立，1948年Rivlin[6]从唯象学的角度出发提出了针对各向同性超弹性材料应变能函数：

Mooney-Rivlin本构模型由于形式简单，容易通过实验进行验证，因此在工程上有着广泛的应用.在长期的研究中积累了大量的理论和实验结果，为后续的新本构模型的建立奠定了基础.该模型能较好拟合不可压缩橡胶材料小变形和中等应变范围的材料力学行为，但不能精确的描述产生硬化现象的橡胶类材料的力学行为以及描述在大变形中应力-应变曲线的“陡升”行为，为了解决这些问题，人们构造对数型和幂指数型的本构模型[8-9].

1997年高玉臣[10]从材料的抗拉和抗压角度，给出一种橡胶类材料的应变能函数，并基于此本构模型对橡胶类材料的裂尖场进行了分析.然而，在不可压缩条件下，此应变能函数既不能简化为Neo-Hookean材料，也不能简化为Mooney-Rivlin材料.这影响着应变能函数应用的实验基础.高玉臣基于此本构模型对橡胶缺口与刚性楔体之间的大变形接触问题，集中力作用下橡胶楔体的拉伸问题，橡胶类材料的界面裂纹，大应变弹性体的应力以及奇异性进行了分析[11-14].Long R[15]基于此本构模型对软弹性体的裂尖场进行了准大变形分析.Sang JB[16]对此本构模型进行了修正，基于有限变形理论对含空洞圆形橡胶薄膜的大变形问题进行了分析.

在本文中，借鉴高玉臣的本构模型，建立一个描述不可压缩橡胶类材料的新的本构模型.当n=1且α =0时，新模型转化为Neo-Hookean模型，而当n=1且α=1时，新模型转化为Mooney-Rivlin模型.通过对均匀变形进行分析和计算，考察了新模型的合理性和适用性.给出橡胶类材料的单轴拉伸以及橡胶圆管受内压膨胀两个特例，讨论了两个本构参数对材料行为的影响.

1 本构模型的修正

1997年高玉臣给出应变能函数[10]：

基于有限变形理论可得Cauchy应力张量的表达式为

基于本构模型式（2），对不可压缩橡胶类材料，给出了修正后的应变能函数

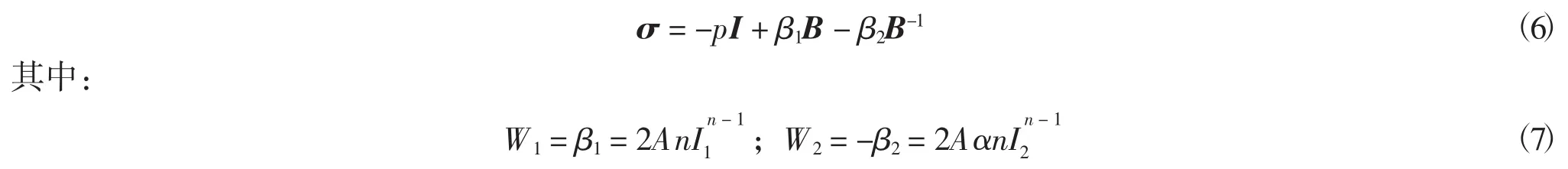
对于新的本构模型式（4）的合理性，做如下讨论.首先，式（4）满足在刚性条件下，这意味着参考构形是自然构形.其次β1和β2满足∂β1/∂I2+∂β2/∂I1=0即材料是超弹性的.再次，1975年Batra提出对各向同性材料进行单轴拉伸时，其本构模型需满足经验不等式，β1>0，β2≤0，Rivlin、Saunders和Treloar等人的试验数据都说明这个经验不等式是成立的，显然，由式（7）可以看出，当A>0，n>0，α≥0时，β1≥0；β2≤0成立.最后讨论新的本构模型是否满足Baker-Ericksen不等式，这是1962年由Truesdell和Noll提出的.对于各向同性材料，较大的主应力应该产生在较大的主伸长[1]，即

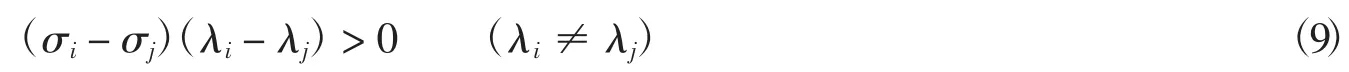
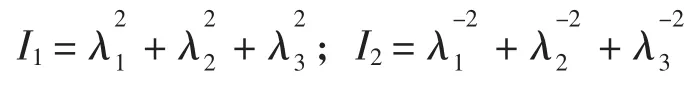
不可压缩条件为

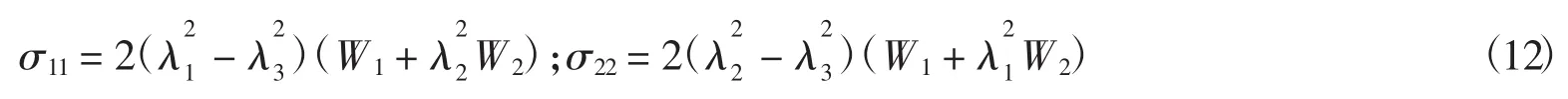
由不可压缩条件（11）得到

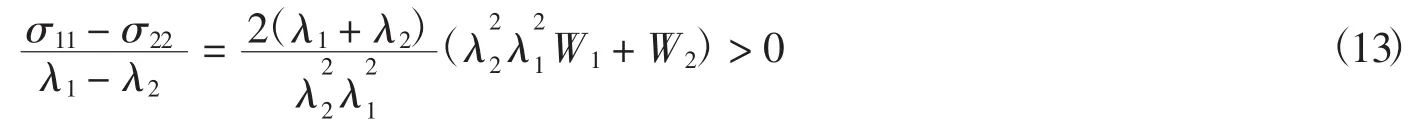
2 橡胶类材料的单向拉伸

为不失一般性，考虑一个有限变形材料的立方单元体.如图1所示.

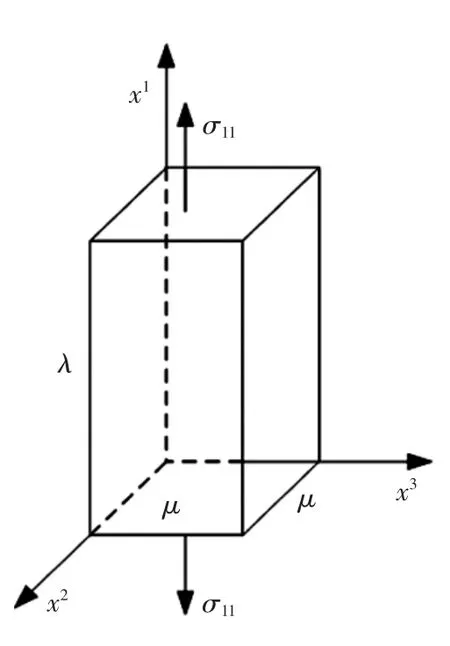
图1 单轴变形示意图Fig.1 The uniaxial deformation diagram

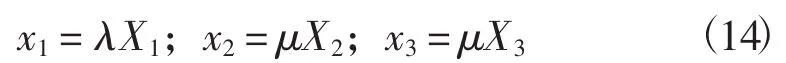
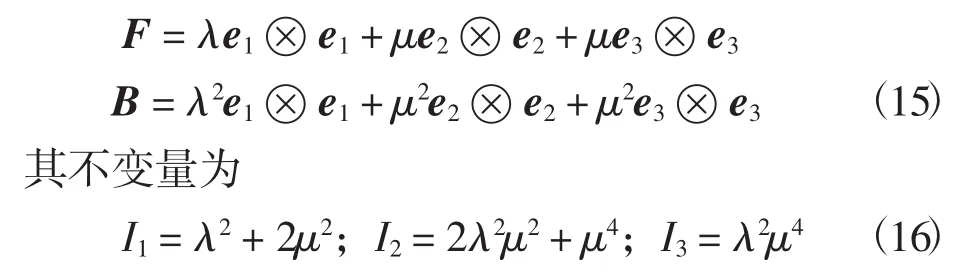
由本构关系式（5）可得分量形式

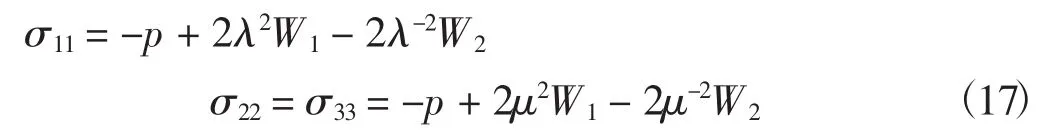
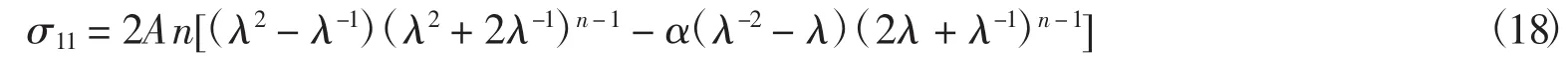
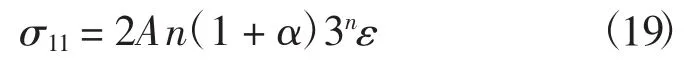
为了讨论本构参数α和n对材料力学性能的影响，引入无量纲化的作用力F/A，由方程（18）得出：

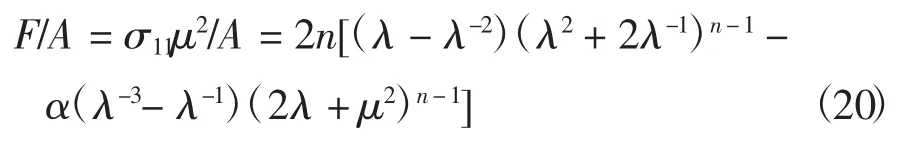
对方程（20）的计算结果由图2和图3给出.

3 内压作用下橡胶圆管的变形分析

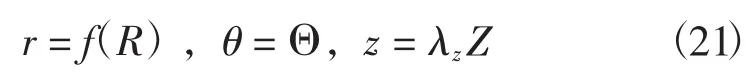
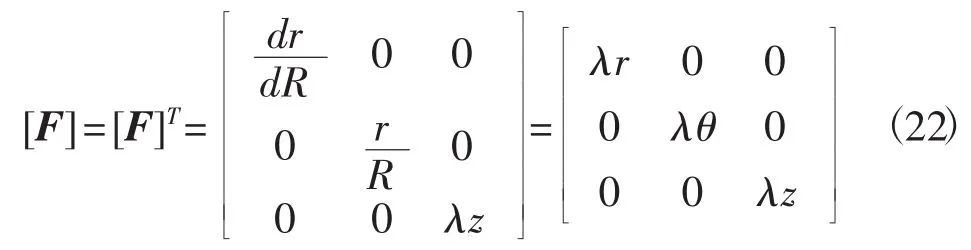
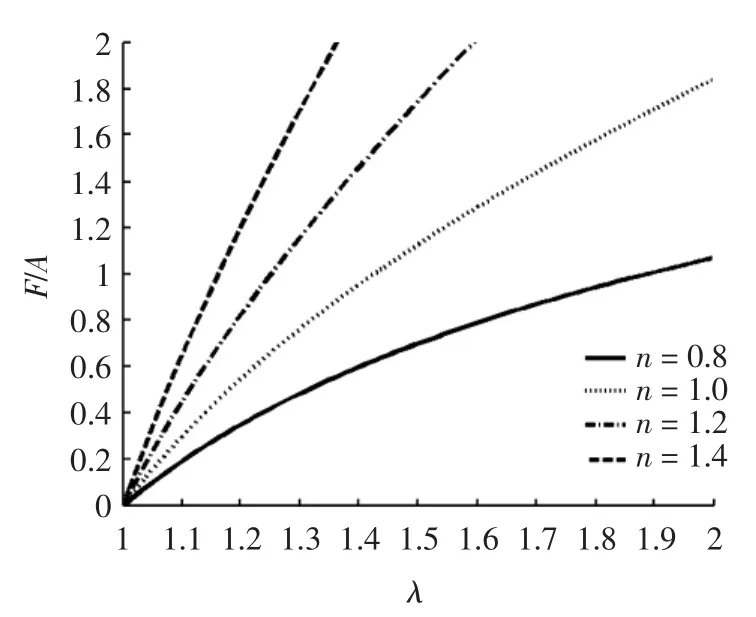
图2 本构参数n对F/A-λ关系曲线的影响（α=0.1）Fig.2 The relation between F/A-λ with effect of n（α=0.1）

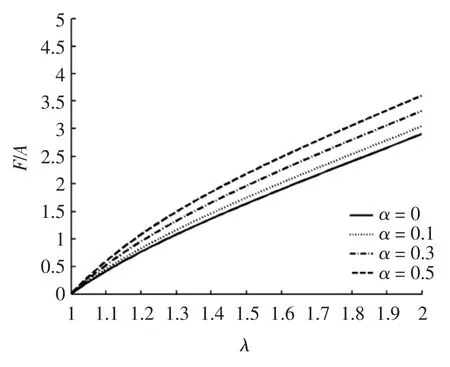
图3 本构参数α对F/A-λ关系曲线的影响（n=1.2）Fig.3 The relation between F/A-λ with effect of α（n=1.2）

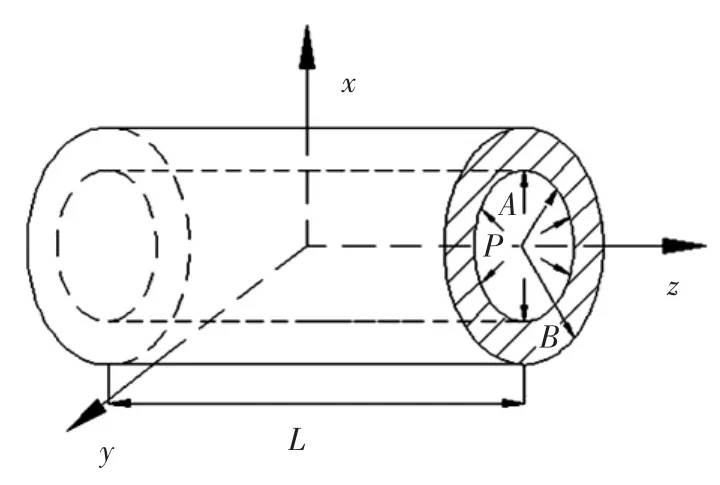
图4 受内压橡胶圆管模型示意图Fig.4 Rubber tube model diagram under pressure

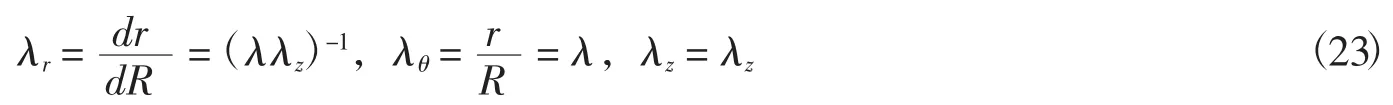
其左柯西-格林应变张量以及3个应变不变量可表示为

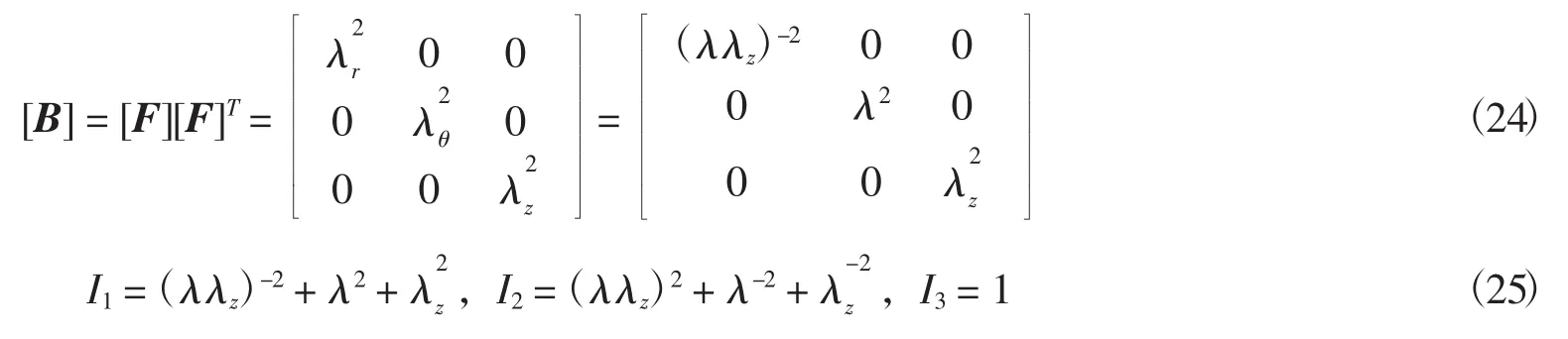
由式（5）可以得到各Cauchy应力分量为

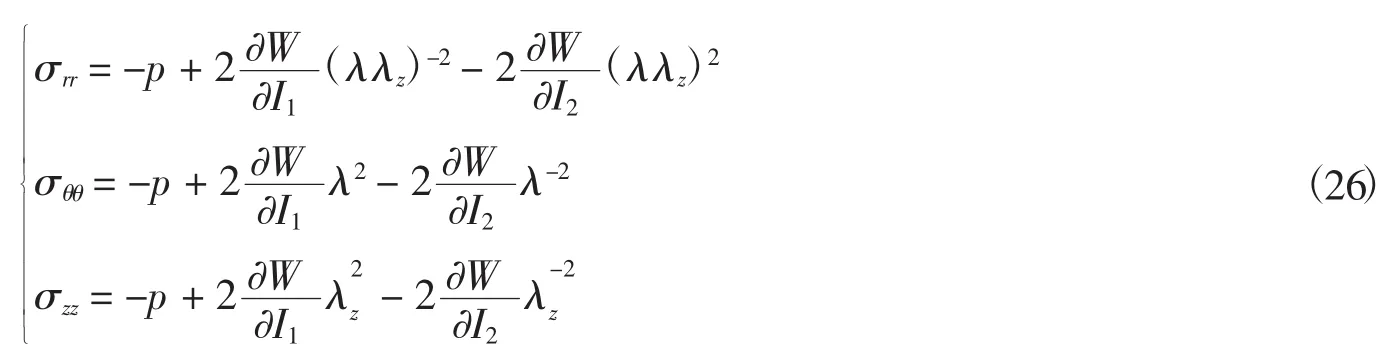
将式（27）代入式（26）可得：

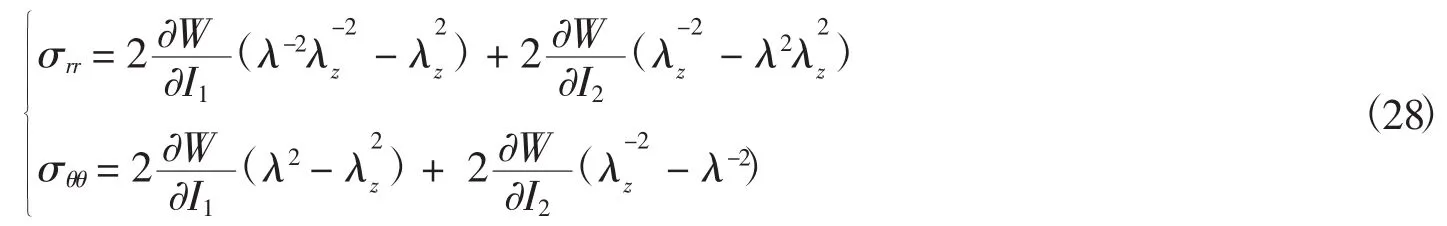
在柱坐标系下，不计体力的影响，并由轴对称条件得到径向平衡方程为

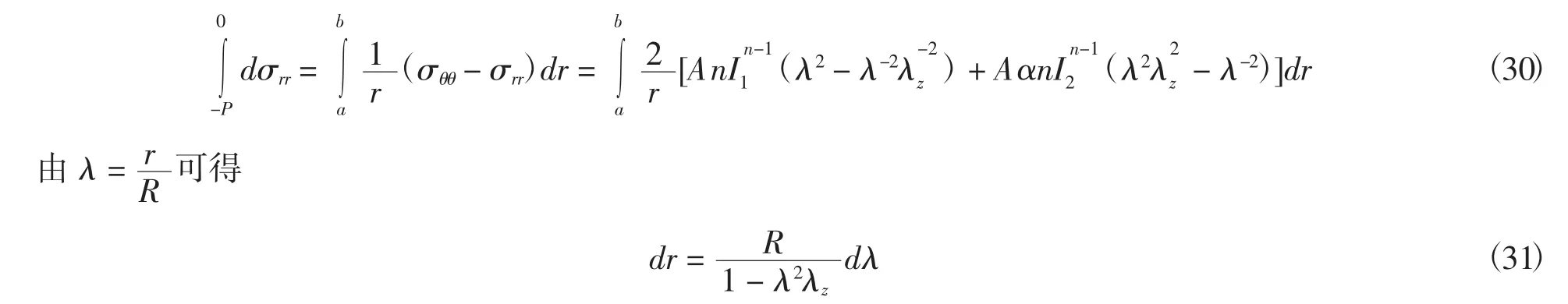
将式（31）代入式（30）可得膨胀压力的表达式为

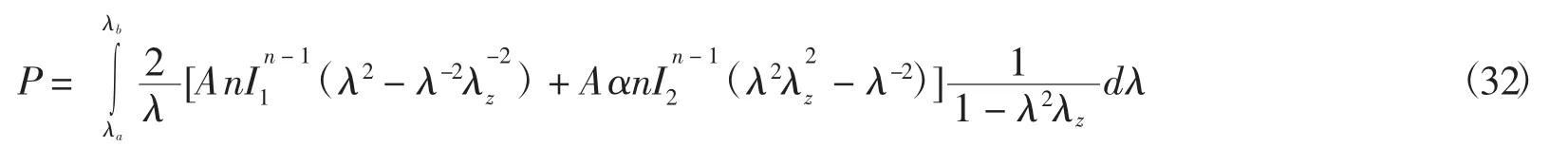
将式（33）代入式（32），经过化简可得

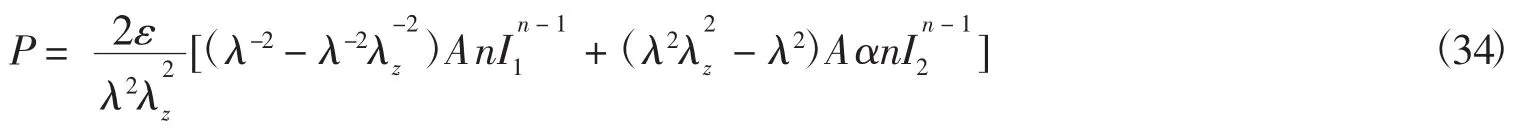
将膨胀压力P进行无量纲化处理可得

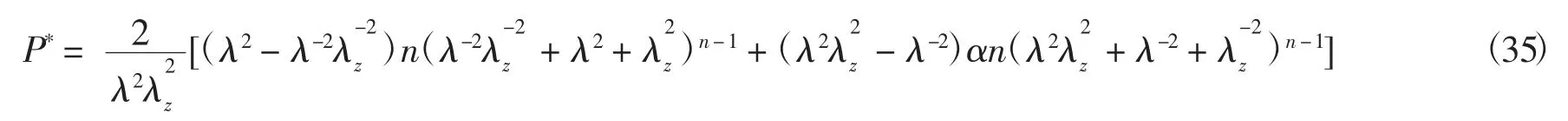
4 结论

基于有限变形的基本理论，对高玉臣所提出的橡胶类材料的本构模型进行修改，给出1个新的不可压缩超弹性应变能函数.由于引入参数α和n，使描述材料的模型具有更大的实用范围.当n=1且α=0时，新的本构模型转化为Neo-Hookean模型，而当n=1且α=1时，转化为Mooney-Rivlin模型.对于橡胶类材料的单轴拉伸，给定本构参数α，随着本构参数n增加，应力增大，明显的具有强化特征，当n=1.4出现在大变形中应力-应变曲线的“陡升”行为；给定本构参数n，α控制了I2对于材料变形和应力的影响，对于给定的n=1.2，随着α的增加，应力相应的也会增加，但影响的效果较强化参数n的影响的效果小.对于橡胶圆管受内压膨胀问题，固定α和λz，当n取较小值时，橡胶圆管具有较大的环向主伸长，表示橡胶圆管的膨胀能力较强，韧性较好，尤其当n<1时，橡胶软管出现了失稳现象.当n取较大值时，橡胶圆管具有较小的环向主伸长，随着n的增加，内压增加明显，具有明显的强化特征；固定n和λz，α同样控制了I2对于材料变形的影响，随着α的增加，内压相应地增加，但影响的效果较强化参数n的影响效果小.

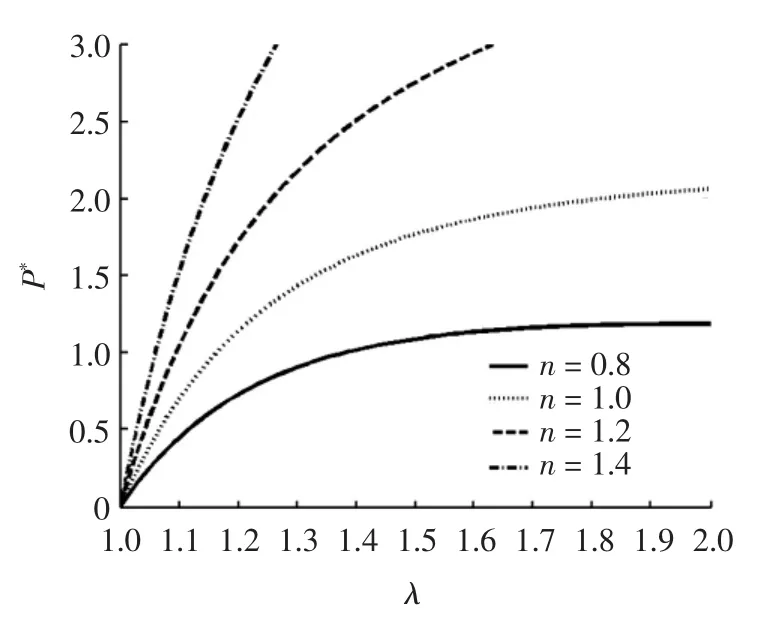
图5 本构参数n对P*-λ曲线的影响Fig.5 The Relation between P*and λ for different n

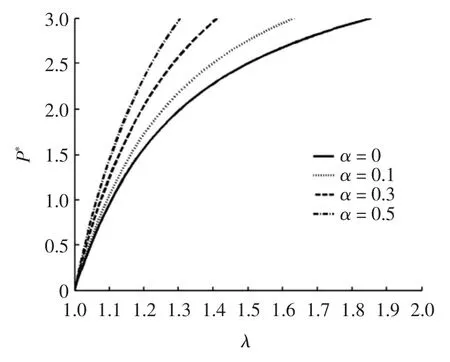
图6 本构参数α对P*-λ曲线的影响Fig.6 The Relation between P*and λ for different α

[1]Beatty M F.Topics in finite elasticity：hyperelasticity of rubber，elastomer，and biological tissues-with example[J].Applied Mechanics Review，1987，40（12）：1699-1734.

[2]Fuzhang Zhao.Continuum constitutive modeling for isotropic hyperelastic materials[J].Advances in Pure Mathematics，2016，6，571-582.

[3]EhretAE.OnamolecularstatisticalbasisforOgden'smodelofrubberelasticity[J].Journal of the Mechanics and Physics of Solids，2015，78：249-268.

[4]Yükseler R F.A theory for rubber-like rods[J].International Journal of Solids&Structures，2015，69-70：350-359.

[5]Li F，Liu J，Yang H，et al.Numerical simulation and experimental verification of heat build-up for rubber compounds[J].Polymer，2016，101：199-207.

[6]Rivlin R S.Large elastic deformations of isotropic materials.ii.some uniqueness theorems for pure，homogeneous deformation[J].Philosophical Transactions of the Royal Society B Biological Sciences，1948，240（822）：491-508.

[7]黄筑平.连续介质力学基础[M].北京：高等教育出版社，2003.

[8]Gent A N.A new constitutive ralation for rubber[J].Rubber Chemistry and Technology.1996，69（1）：59-61.

[9]Horgan C O，Saccomandi G.A molecular-statistical basis for the Gent constitutive model of rubber elasticity[J].J Elasticity，2002，68（1）：167-176.

[10]Gao Y C.Large deformation field near a crack tip in rubber-like material[J].Theoretical&Applied Fracture Mechanics，1997，26（3）：155-162.

[11]Gao Y C，Gao T J.Large deformation contact of a rubber notch with a rigid wedge[J].International Journal of Solids and Structures，2000，37（32）：4319-4334.

[12]Gao Y C，Chen S H.Analysis of a rubber cone tensioned by a concentrated force[J].Mechanics Research Communications，2001，28（1）：49-54.

[13]Gao Y C.Analysis of the interface crack for rubber-like materials[J].Journal of Elasticity，2002，66（1）：1-19.

[14]Gao Y C，Jin M，Dui G S.Stresses，singularities，and a complementary energy principle for large strain elasticity[J].Applied Mechanics Reviews，2011，61（61）：683-695.

[15]Long R，Hui C Y.Crack tip fields in soft elastic solids subjected to large quasi-static deformation-A review[J].Extreme Mechanics Letters，2015，4：131-155.

[16]Sang JB，Xing SF，Tian HY et al.Research on mechanical properties of a polymer membrane with a void based on the finite deformation theory[J].e-Polymers，2015，15（5）：293-299.

[责任编辑田丰 夏红梅]

Analysis of hyperelastic mechanical property on rubber like materials under basic load

SANG Jianbing,LIU Yanyong,XING Sufang,WANG Jingyuan,FU Shuangjian
（School of Mechanical Engineering，Hebei University of Technology,Tianjin 300130,China）

Based on the finite deformation theory,analysis of hyper elastic mechanical property on rubber like materials under basic load has been proposed.A new constitutive model modified from Gao's second constitutive model has been introduced by utilizing the finite deformation theory.In the circumstance that material is incompressible,when and,the new constitutive relation may be simplified to Mooney-Rivlin model;when and,the new constitutive relation may be simplified to Neo-Hookean model.By utilizing the new constitutive relation,super elastic mechanical properties of the rubber materials has been researched under basic loads,which include the uniaxial tension and inflation under internal pressure.The influence of constitutive parameters has been analyzed,which has been pointed out that is the intensive parameter of the materials.Rubber tube has the phenomenon of instability under internal pressure.Its stability is not only dependent on the constitutive parameter but also related to the constitutive parameter α.

rubber like materials;constitutive model;finite deformation theory;uniaxial tension;inflation under internal pressure

U465

A

1007-2373（2017）02-0036-06

10.14081/j.cnki.hgdxb.2017.02.007

2016-12-05

河北省教育厅自然科学重点项目（ZD20131019，ZD2016083）；天津市科技特派员项目（16JCTPJC53100）

桑建兵（1974-），男，教授，sangjianbing@hebut.edu.cn.