基于方向启发性的路径查找模型研究
2017-06-23影0
周 影0
淮北师范大学计算机科学与技术学院,淮北,235000
基于方向启发性的路径查找模型研究
周 影0
淮北师范大学计算机科学与技术学院,淮北,235000
提出了一种在起点和终点的方向关系已知的前提下的路径查找模型。查找过程从起点开始,计算其邻接点与终点的方向关系,利用优劣评价函数逐一计算出各经历顶点的最优邻接点,由若干最优邻接点组成的顶点序列就是所找路径。结果表明:该模型依托的方向关系可以有效提高陌生环境的路径查找效率,同时模型的稳定性和准确率也都较高。
路径查找;优劣评价函数;方向关系;模型;邻接点
1 问题的提出
路径查找是确定出起点到终点之间的一条路径,并沿路径而行的心理过程,它的最终目标是找到由起点到达终点的一条路径[1]。对于路径查找,很多国外的学者和专家提出了多种模型。Moise Busogi等提出一种人类理性行为基础上的路径查找建模方法,通过对人的行为评估,在执行层面上感知物理环境[2]。Beatrix Emo提出并强调空间几何角色对个人空间决策的重要性,并在城市环境中实现了路径查找[3]。但国内研究路径查找模型的较少,齐平、李龙澍提出一种基于信任机制的动态商拓扑模型,该模型拓扑结构在随时间变化的情况下,使用贝叶斯方法评估节点可信度[4]。苏加强、丁柳云基于遗传算法,提出了查找最优路径的算法[5]。赵开新、王东署等人提出基于蚁群遗传算法的移动机器人路径规划算法,旨在改进初期搜索盲目性大等问题[6]。
以上文献都在实验中说明方法的有效性,但均未针对方向启发信息进行路径查找。为此,本文提出一种以方向启发为前提的路径查找模型,假设前提为已知起点和终点的方位,一步步找出起点到终点的最优邻接顶点,这些顶点组成了所找路径。
2 方向关系和优劣评价函数解析
此模型中,假设知道起点(SV)和终点(EV)的方向关系,从起点出发,找出起点的邻接点(AV),利用邻接点和终点的方向关系是否接近于起点和终点的方向,进而确定出最优邻接点。
2.1 方向关系
模型中的方向关系有8种,东、南、西、北为4个基本方位,东南、西南、西北、东北为4个辅助方位,其位置关系如图1所示。

图1 方向关系图
2.2 优劣评价函数
路径查找的关键是通过计算找出最优邻接点,最优邻接点可使用优劣评价函数计算得出。函数的定义:如果起点与当前点(CV)的方向关系等于起点与终点的关系,那么该当前点的评价函数值最大;如果起点与当前点的方向关系和起点与终点的方向关系是相关的,它的评价函数值取中间值;如果起点与当前点的方向关系和起点与终点的关系是无关的,那么它的评价函数值就是最小的。这里所说的相关,应理解为相近,比如起点与终点的方向关系是东南,起点与当前点的方向关系是东或南,那么就认为它们是相关的;相反,比如起点与终点的方向关系是正东,起点与当前点的方向关系是东北或东南,此时也认为它们是相关的。
Fun (SV,CV) {
If (Relation(SV,CV))∩(Relation(SV,EV))= Relation(SV,EV)) return max;
If (Relation(SV,CV))∩(Relation(SV,EV))∈Relation(SV,EV)) return middle;
If (Relation(SV,CV))∩(Relation(SV,EV))=∅return min;
};
如果起点与当前点的方向关系和起点与终点的方向关系是一致的,且符合条件的当前点不止一个顶点时,就按存储时第一个存储的当前点作为最优邻接点。
2.3 假设场景解析
图2为假设场景,场景中A是起点,B是终点,A1、A2、A3、A4是起点A的邻接点,Relation(A,B)=WS。
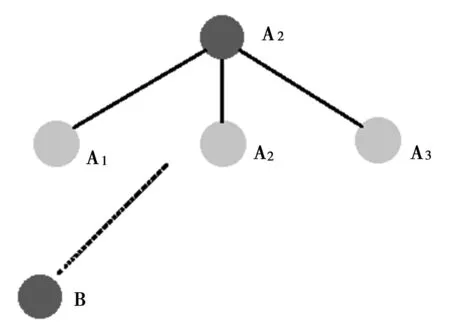
图2 假设场景
(1)分别计算三个邻接点与A的方向关系:
Relation(A,A1)=WS, Relation(A,A2)=S, Relation(A,A3)=ES;
(2)计算三个邻接点与起点的方向关系的评价函数:
Fun(A,A1)=max,Fun(A,A2)=middle,Fun(A,A3)=min;
(3)比较三个评价函数的大小,选取评价函数值大的点作为下一步需要访问的顶点,因为Fun(A,A1)>Fun(A,A2)>Fun(A,A3),所以A1的评价函数值最大,故A1是最优邻接点。
A1为起点之后的计算得到下一个的顶点,然后再以A1作为新的起点,计算A1的邻接点中的最优者,一步步执行,直到顶点和终点相同结束。
3 基于方向启发式的路径查找模型
3.1 模型的实现步骤
模型的实现依托一个相对完整的环境,把环境转换为道路图,图中有顶点集、边集、图层,算法步骤如下:
Step1 定义顶点Vertex的数据类型,定义与顶点类型相同的队列,用于存储路径查找过程中的诸多最优邻接顶点;
Step2 初始化道路图中所有顶点个数N(int N≥2);
Step3 输入起点SV和终点EV,和两者的位置关系Relation (SV,EV);
Step4 如果N=2,输出SV→EV那条路径;如果N>2,转向Step5;
Step5 利用优劣评价函数计算起点的每个邻接点的函数值,从中选出最优邻接点作为下一个访问对象AV′,同时将此邻接点存入队列中;
Step6 如果AV′=EV,输出队列里的所有顶点,顶点序列就是所求的路径;如果AV′!=EV,把AV′作为新的顶点,转向Step5。
3.2 实验结果与分析
MapXtreme是MapInfo公司开发的基于网络的应用服务器,它具有强大的地图化功能,包括地图编辑、地图显示、图层控制等[7-8]。以下使用MapXtreme作为界面工具,以淮北师范大学校园为模拟环境。将校园平面图构造成由顶点和直线路径组成的实验用图,为了直观,把各建筑物用类实物图显示。实验中,以学校大门(存储名为node1)为起点,学生第二食堂(存储名为node62)为终点,输入两者的方位关系为西南方向(WS),执行界面如图3所示,粗虚线即为所求路径。

图3 基于方向启发的路径查找模型实验图
4 结 论
在起点和终点的方向关系已知的基础上,从起点开始,利用最优评价函数计算出最优邻接点,直到找出到终点的路径位置。该模型的实现是在学校环境里,经过多次比较和测试,该模型在时间上是高效的,同时稳定性和准确率也都较高。从问题的系统性上考虑,在今后的研究工作中可考虑增加顶点的信息存储量、道路权值等信息,可提高问题的精准度。
[1]David M Mark,Christian Freksa,Stephen C.Hirtle,et al.Cognitive models of geographical space[J].International Journal of Geographical Information Science,1999,13(8):747-774
[2]Moise Busog,Namhun Kim,Dongmin Shin,et al.Bayesian Affordance-Based Agent Model for Wayfinding Behaviors in Evacuation Problems[C].Berlin:4th International Conference of HCI International,2013:297-306
[3]Beatrix Emo.Wayfinding in Real Cities:Experiments at Street Corners[C].Berlin:International Conference of Spatial Cognition,2012:461-477
[4]齐平,李龙澍.动态商拓扑模型及其在路径查找中的应用[J].模式识别与人工智能,2014,24(7):337-344
[5]苏加强,丁柳云.基于遗传算法的GIS辅助最优路径查找算法[J].辽宁科技学院学报,2012,14(4):23-25
[6]赵开新,王东署,徐立新.蚁群遗传算法在移动机器人路径规划中的综合应用研究,制造业自动化,2014,36(9):70-72,84
[7]孙龙,曹菡.基于MapXtreme的候机楼导航和监控系统的设计与实现[J].计算机科学与发展,2011,21(5):183-186
[8]吴开兴,范周艳.MapXtreme下WebGIS的优化研究[J].测绘通报,2015,(7):109-112
(责任编辑:汪材印)
10.3969/j.issn.1673-2006.2017.04.032
2017-02-01
安徽省教育厅高校自然科学研究重点项目“安全协议的形式化分析方法研究”( KJ2017A848)。
周影(1981-),女,安徽淮北人,硕士,讲师,研究方向:GIS,信息安全。
TP301.6
A
1673-2006(2017)04-0115-03
